路口場景下基于Bezier和VFH的無人車軌跡規劃方法與流程

本發明涉及智能交通系統技術領域，特別涉及無人駕駛車輛在路口這樣的復雜交通場景下的實時軌跡規劃方法。

背景技術：

隨著汽車產業和計算機技術的飛速發展，無人駕駛車輛在機器人領域里取得了空前的進步。決策系統做為無人駕駛車輛的“大腦”，在感知系統認知周圍環境后，需要做出安全可執行的決策，確定當前的有效行為及行為的目標狀態，然后規劃運動軌跡。路口是交通網絡拓撲結構的節點，是交通事故的頻發地段。所以，解決無人車在路口處的軌跡規劃問題意義重大。經典的軌跡規劃方法分為兩大類，一類是直接有解析解，基于多項式、正弦曲線、回旋曲線、bezier曲線等方法確定參數直接生成軌跡的解析解；第二類方法是基于采樣的方式生成由離散點組成的軌跡，有a*、rrt、人工勢場法，vfh等多種方法解決不同環境中的軌跡規劃問題。

bezier是解析法生成軌跡的典型方法。其優點是在無障礙物或者障礙物稀疏時，生成軌跡快且平滑性好。缺點在于障礙物密集時難于通過調整參數獲得有效軌跡[1]。

a*算法是經典的運動規劃算法，其優點是具有啟發性，能夠較快的得到全局最優軌跡，然而其搜索步長難以確定，在復雜并且范圍較大的規劃環境中效率低下[2]。

rrt算法是由美國uiuc教授s.m.lavalle提出的，該算法在擴展節點時考慮了運動系統的運動學微分方程約束，因此，生成的運動軌跡滿足全局最優約束和系統自身微分約束，可見，rrt算法可以很好的解決高維度、動態環境、含有微分約束的運動規劃問題，然而，其需要確定的參數數量較多，要達到比較好的規劃效果，往往難度較大[3]。

人工勢場法是軌跡規劃算法中較成熟且高效的規劃方法，它將環境信息轉化為引力場和斥力場模型。人工勢場法的一個缺陷就是當目標在障礙物的影響范圍內時，整個勢場中除目標點外還可能存在其它的局部極小點，機器人可能陷入局部極小點而不能達到目標點。此外，軌跡經過障礙物附近時由于合力方向變化產生抖動現象。

vfh算法將機器人的工作環境分解為具有二值信息的柵格單元，每個矩形柵格中有一個累積值，表示在此處存在障礙物的可信度，高的累積值表示存在障礙物的可信度高。柵格選得小，環境信息存儲量大，決策速度慢；柵格選得大，環境分辨率下降，在障礙物環境中發現軌跡的能力減弱[4]。

vfh算法具有很強的避障能力，能夠在復雜多障礙物環境中找到無碰撞的運動軌跡；在路口這樣復雜的環境下適合使用柵格圖進行環境建模，而vfh算法恰好是基于障礙物柵格表示的運動規劃方法；vfh算法的規劃空間是連續的，這方便將車輛的運動學約束加進來[5]。

然而，vfh算法是為移動機器人設計的，直接使用在無人駕駛車輛上往往達不到預期的目標，主要有以下三個問題：原始vfh算法是一種基于感知數據的實時運動規劃方法，直接使用必然導致運動軌跡不平滑而出現“震蕩”現象[6]；原始vfh算法活動區域中的部分運動狀態點對無人駕駛車輛來講是不可達的；vfh算法得到的是稀疏的位置點集，缺乏其它運動狀態信息，不能引導車輛行駛[7]。

以下給出檢索的相關文獻：

[1]l.han,h.yashiro,h.t.n.nejad,q.h.do,ands.mita,“beziercurvebasedpathplanningforautonomousvehicleinurbanenvironment,”in2010ieeeintelligentvehiclessymposium(iv).ieee,2010,pp.1036–1042.

[2]huynn,dechterr,pearlj.probabilisticanalysisofthecomplexityofa*[j].artificialintelligence,1980.15(3):241～254.

[3]lavallesm,kuffnerjj.rapidly-exploringrandomtrees:progressandprospects[c]//4thinternationalworkshoponalgorithmicfoundationofrobotics.wellesley,usa:akpe-ters,2000:293-308.

[4]j.borensteinandy.koren,“thevectorfieldhistogram-fastobstacleavoidanceformobilerobots,”ieeetransactionsonroboticsandautomation,vol.7,no.3,pp.278–288,1991.

[5]i.ulrichandj.borenstein,“vfh+:reliableobstacleavoidanceforfastmobilerobots,”in1998ieeeinternationalconferenceonroboticsandautomation.ieee,1998,pp.1572–1577.

[6]i.ulrichandj.borenstein,“vfh*:localobstacleavoidancewithlook-aheadverification,”in2000ieeeinternationalconferenceonroboticsandautomation.ieee,2000,pp.2505–2511.

[7]d.jiea,m.xueming,andp.kaixiang,“ivfh*:real-timedynamicobstacleavoidanceformobilerobots,”in201011thinternationalconferenceoncontrolautomationroboticsandvision(icarcv).ieee,2010,pp.844–847.

技術實現要素：

本發明的目的在于提供一種路口場景下基于bezier曲線和vfh方法的無人車實時軌跡規劃方法，解決上述現有理論與技術上存在的缺陷或不足。本發明用三階bezier曲線做為無人駕駛車輛的行駛軌跡；同時對傳統vfh算法做出改進，將vfh算法和bezier曲線相結合，克服vfh算法的缺陷；并且用分層的思想將兩種運動規劃方法同時用于路口的軌跡規劃，劃分優先級。

為達到用三階bezier曲線做軌跡規劃，本發明采用了以下技術方案:

1、路口場景下基于bezier曲線和vfh方法的無人車實時軌跡規劃方法，包括以下步驟：

步驟一，從行為決策層獲取當前行為方式及本次軌跡規劃的起始點位姿p0(x0,y0,θ0)和目標點位姿p3(x3,y3,θ3)；

步驟二，采用三階bezier曲線模型生成從起始點p0到目標點p3的軌跡簇a1采用三階bezier曲線模型生成從起始點p0到目標點p3的軌跡簇a1，選擇4個控制點的三階bezier曲線進行規劃，根據車輛端點處的最小轉彎半徑求出p0p1和p2p3的下限，同時我們依據線段|p0p3|的長度確定p0p1和p2p3的上限，在得到控制點p1和p2的范圍后，在范圍內等間隔離散的取多個不同的p1和p2，得到多組控制點，進而得到多條滿足端點曲率約束的幾何軌跡，稱之為軌跡簇，用a1表示。

步驟三，在得到滿足曲率約束的軌跡之后，進行碰撞檢測，得到無碰軌跡簇a3。若無碰軌跡簇非空，則順序進行步驟四。若無碰軌跡簇為空，進入步驟五；

步驟四，選擇最優軌跡

在得到滿足曲率約束并無碰的軌跡之后，我們需要進一步選擇最優軌跡。以軌跡最平滑為標準選擇最優軌跡，可抽象成

步驟五，對原始vfh算法中的活動區域進行改善

rmin表示車輛的最小轉彎半徑，s表示車輛行進過程中的搜索步長；

步驟六，利用障礙物信息建立柵格圖

由于障礙物被抽象成一個box，收到的障礙物信息是box的四個角點坐標，因此可根據四個角點建立柵格圖，以柵格圖正中心為原點建立坐標系，將box的四個角點坐標映射到柵格圖坐標系中；

步驟七，將扇形活動區域劃分成多個扇區，并判斷是否有障礙物占據

對于柵格圖上每一個被障礙物占據的柵格，將它們抽象成一個質點，判斷該柵格是否落入扇形區域中；若落入，判斷是落入到哪一個扇區中，否則認為該障礙物目前不在搜索范圍內，最終對每個扇區的被障礙物占據的柵格個數做出統計；

步驟八，與bezier曲線相結合選擇最優軌跡點

如果有多個扇區都是可行的，那么將選擇一個最優的扇區所對應的軌跡點，這里主要有兩個約束條件來篩選出最優軌跡點。一是考慮車寬，二是考慮目標點位姿。

步驟九，離散點集做控制點生成b樣條曲線

b樣條的數學模型描述如下：

式中，pi,n(t)表示第i+1個n階b樣條曲線片段；n表示b樣條曲線的階數；t為參數，取值為[0,1]；pi+k為控制點；fk,n(t)為b樣條基函數。

b樣條的數學模型描述如下：

式中，pi,n(t)表示第i+1個n階b樣條曲線片段；n表示b樣條曲線的階數；t為參數，取值為[0,1]；pi+k為控制點；fk,n(t)為b樣條基函數。

所述的采用三階bezier曲線模型生成從起始點p0到目標點p3的軌跡簇a1，選擇4個控制點的三階bezier曲線進行規劃，根據車輛端點處的最小轉彎半徑求出p0p1和p2p3的下限，同時我們依據線段|p0p3|的長度確定p0p1和p2p3的上限，在得到控制點p1和p2的范圍后，在范圍內等間隔離散的取多個不同的p1和p2，得到多組控制點，進而得到多條滿足端點曲率約束的幾何軌跡，稱之為軌跡簇，用a1表示。

與bezier曲線相結合選擇最優軌跡點，使其逼近目標點位姿并且軌跡足夠平滑，即從a2篩選出最光滑的一條曲線作為參考軌跡，vfh算法搜索軌跡點的過程中，在滿足車寬的情況下，總是尋找最貼近參考軌跡的點，即所有可行扇區中離參考軌跡距離最短的點，作為最優軌跡點。

本發明的創新點在于將解析方法(對應bezier曲線)和離散方法(對應vfh算法)結合起來，使無人車在避障的同時，又能夠沿著光滑的路徑以期望的位姿達到目標點，避免了無人車駛出路口后由于朝向角的偏差引起震蕩。

附圖說明

圖1是本發明的流程示意圖；

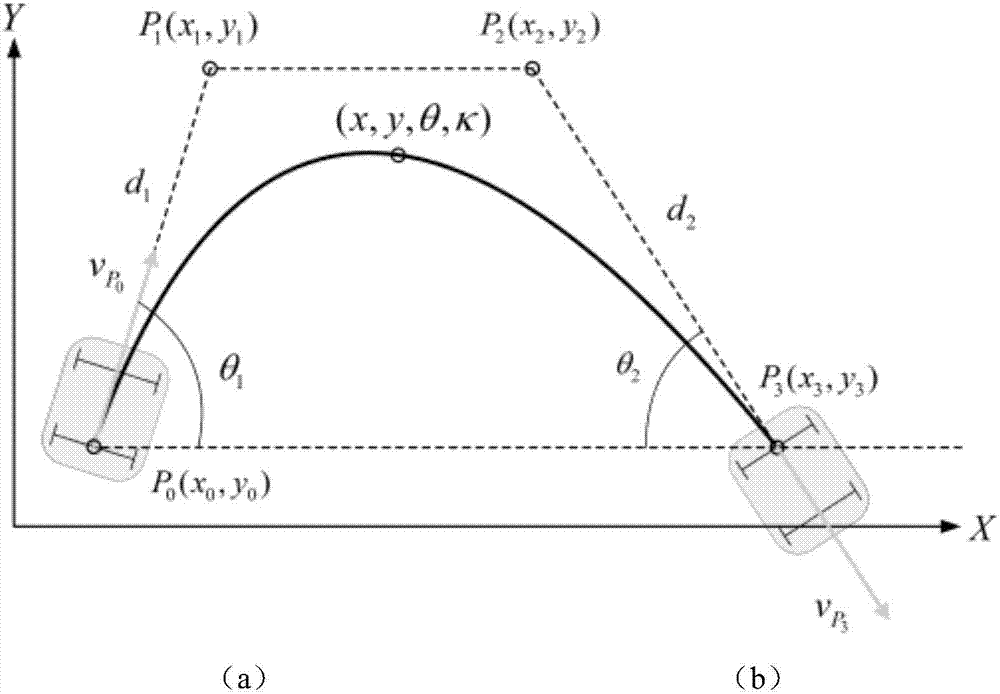
圖2是三階貝塞爾曲線的生成示意圖；

圖3是vfh算法中無人車的活動區域改進示意圖；

圖4是將障礙物信息映射到柵格圖坐標系下的示意圖；

圖5是將活動區域分成多個扇區，并判斷每個扇區是否被障礙物占據的示意圖，其中，紅色線對應的扇區表示被障礙物占據；

圖6是基于貝塞爾曲線選擇最優軌跡點的示意圖，其中，粗線表示貝塞爾曲線，圓弧上距離該粗線最短的點是最優軌跡點。

具體實施方式

下面結合附圖對本發明作進一步說明。

參見圖1，基于分層思想的路口運動規劃方法分為兩部分，包括的各個步驟如下：

1)根據起始點和目標點位姿信息規劃bezier曲線，具體步驟如下：

(1a)從感知處獲取起始點和目標點的位姿信息x,y,θ(x坐標，y坐標，朝向角)；

(1b)尋找合適的，多種組合的控制點，生成多條bezier曲線；

bezier曲線的數學模型如下所示。

bezier曲線是一種特殊的多項式曲線，假設給定n+1個控制點pi(i＝0,1,....,n)，則n階bezier曲線可以表示為：

其中bi,n(t)為n階伯恩斯坦基底多項式，其數學定義為：

其中，n為bezier曲線的階數；t是控制參數，取值范圍為[0,1]；pi表示第i+1個控制點。參數t在[0,1]范圍內連續變化，則得到n階bezier曲線。依次連接控制點pi，得到的凸多邊形稱之為控制多邊形，其中p0和pn分別為第一個和最后一個控制點，bezier曲線必然在控制多邊形內部。

根據公式1‐1和1‐2，得到3階bezier曲線的x,y坐標分別為：

x(t)＝x0(1-t)³+3x1t(1-t)²+3x2t²(1-t)+x3t³,t∈[0,1]

y(t)＝y0(1-t)³+3y1t(1-t)²+3y2t²(1-t)+y3t³,t∈[0,1]

整理成關于參數的三階多項式有：

x(t)＝[(x3-x0)+3(x1-x2)]t³+3(x0-2x1+x2)t²+3(x1-x0)t+x0,t∈[0,1]

y(t)＝[(y3-y0)+3(y1-y2)]t³+3(y0-2y1+y2)t²+3(y1-y0)t+y0,t∈[0,1]

為了表示方便，將公式簡化成如下形式：

x(t)＝a3t³+a2t²+a1t+a0,t∈[0,1](1-3)

y(t)＝b3t³+b2t²+b1t+b0,t∈[0,1](1-4)

式中，a3＝(x3-x0)+3(x1-x2)，a2＝3(x0-2x1+x2)，a1＝3(x1-x0)，a0＝x0，b3＝(y3-y0)+3(y1-y2)，b2＝3(y0-2y1+y2)，b1＝3(y1-y0)，b0＝y0。

三階bezier曲線的斜率曲線為：

曲率曲線為：

根據圖2，已知起始點位姿p0(x0,y0,θ0)和目標點位姿p3(x3,y3,θ3)，現確定另外兩個控制點p1(x1,y1)和p2(x2,y2)的選取范圍：由公式(1-6)可求得起始點p0處的曲率為

目標點p3處的曲率為

隨著|p0p1|和|p2p3|的增大，軌跡端點處的曲率半徑也會隨之增大，所以車輛端點處的最小轉彎半徑對應著|p0p1|和|p2p3|的下限。即

其中，rmin表示車輛的最小轉彎半徑。同時，我們依據線段p0p3的長度確定|p0p1|和|p2p3|的上限，即|p0p1|≤|p0p3|及|p2p3|≤|p0p3|。因此我們可以確定控制點的選擇有如下約束：

l1≤|p0p1|≤l3，l2≤|p2p3|≤l3

現對|p0p1|和|p2p3|的取值范圍三等分，可以得到4個控制點，即p1(x1,y1)和p2(x2,y2)各有4種取值，用公式表示如下：

對于p1，有：

對于p2，有：

由于p1和p2各有4種取值，因此有4x4＝16種組合的控制點，對應的有16條bezier曲線。若將|p0p1|和|p2p3|的取值范圍n等分，可以得到n+1個控制點，對應的有(n+1)²條bezier曲線。

得到每組控制點后，可以計算出參數方程(1-3)、(1-4)的系數a0,a1,a2,a3以及b0,b1,b2,b3，從而得到bezier曲線方程，即無人車輛的軌跡方程。

(1c)通過曲率約束對多條bezier曲線進行篩選；

得到候選軌跡簇之后，需要依據最大曲率約束對軌跡簇進行篩選，因為在某一條軌跡上存在最小轉彎半徑小于車輛的固有轉彎半徑(低速下是個定值)的點，那么該軌跡對車輛來講是不可行的。由于每一條軌跡都是用位置點集表示的，可根據公式

計算出每一個點的曲率，從而得到每個點的曲率半徑

然后判斷曲線是否存在某點的曲率半徑滿足

r≤rmin

若滿足，則該曲線是不可行的，舍棄該曲線；否則，保留該曲線。

(1d)通過碰撞檢測對多條bezier曲線再一次進行篩選；

通過步驟(1c)篩選后的軌跡，考慮到車輛行進過程中需要避開障礙物，因此還需要對軌跡進一步做碰撞檢測，選出無碰的軌跡。

(1e)若經過(1c)、(1d)步驟篩選后已無剩下bezier曲線，則認為bezier曲線規劃路口可行軌跡失敗，轉用vfh與bezier曲線相結合的方法；否則，通過軌跡最平滑準則在剩余的曲線里篩選出最優的軌跡。

若步驟(1d)篩選后還有滿足要求的曲線，那么我們需要選擇一條最優的曲線做為車輛最終的軌跡；現我們以軌跡最平滑為準則，選出最優軌跡。

首先，根據公式

計算出每一個點的曲率κ，然后根據公式

可以得到曲率平方和最小的那條曲線，該曲線就是最平滑的曲線，同時也是滿足曲率要求，無碰的可行軌跡。

2)若bezier曲線簇都不滿足以上約束，導致不存在期望的軌跡，則用vfh算法與bezier曲線相結合的算法規劃軌跡，具體步驟如下：

(2a)根據車輛運動學模型確定車輛的活動區域；

由圖3可知，根據車輛的最小轉彎半徑rmin以及搜索步長s，可以得到活動區域在車體當前位姿下的極坐標表示：

p表示以車輛后軸中心為坐標原點，航向角方向為零度的極坐標系；

ρ表示活動區域的距離范圍，并且有ρ∈[0,ρmax]，ρmax表示最大活動距離；

表示活動區域的角度范圍，并且有：

則搜索到的軌跡點必然在弧線上。

(2b)從傳感器獲取障礙物信息建立柵格圖；

由于vfh算法是用柵格圖來表征環境的，因此獲取障礙物信息后需要以柵格圖的形式表現出來。

障礙物可以看成是一個box，因此從傳感器處收到的是該box的四個角點坐標，現需要根據這4個坐標點將障礙物映射到柵格圖坐標系中。

如圖4所示，以車體的朝向為x軸正方向，車的后軸中心點為坐標系原點建立右手坐標系做為柵格圖坐標系。假設該柵格圖的尺寸是gridm*gridn，即有gridm行，gridn列；且分辨率是ratio，即每個柵格的長寬都是ratio；4個角點坐標分別是(x1,y1)、(x2,y2)、(x3,y3)、(x4,y4)。首先獲得包圍box的虛線框，步驟如下：令

xmin＝min{x1,x2,x3,x4}，xmax＝{x1,x2,x3,x4}

ymin＝min{y1,y2,y3,y4}，ymax＝max{y1,y2,y3,y4}

可以通過如下公式

計算出虛線框在柵格圖上的位置。其中，rowmin表示虛線框所占據的行的最小值，rowmax表示所占據的行的最大值；colmin表示虛線框所占據的列的最小值，colmax表示所占據的列的最大值。[]符號表示向下取整，比如[1.5]＝1。

計算出rowmin、rowmax、colmin、colmax后，我們就知道了虛線框所包含的每一個柵格的位置。接下來要做的是判斷虛線框里的每一個柵格是否落在box內，具體方法是判斷每一個柵格的四個角點是否存在一個或多個點落入到box內；若存在，則認為該柵格是被障礙物占據的，相應的值用1表示；若不存在，則該柵格未被障礙物占據，相應的值用0表示。

現介紹如何判斷一個點是否落入到凸四邊形內。假設該凸四邊形為abcd，且abcd為順時針，待判斷的點為m，則需要滿足：

abxam>0,bcxbm>0,cdxcm>0,daxdm>0

即可證明點m在凸四邊形內部。

計算出每個柵格對應的0‐1值，相當于建立起了柵格圖。

(2c)將活動區域分成多個扇區，并判斷每個扇區是否有障礙物占據；

假設活動區域的角度為ω，將活動區域分成k個扇區，如圖5所示，則每個扇區的角度為w/k。

現判斷每個被障礙物占據的柵格是否在某個扇區內，具體步驟為：將每個柵格抽象成質點，可以是每個柵格的中心點，假設該柵格處于第row行，第col列，則該柵格的坐標點(x,y)為：

從而可以計算出該柵格與車體的距離，若該距離小于搜索步長s，則用角度繼續判斷是否在扇區內：計算該柵格坐標點與車體坐標點連線所形成的與x軸的夾角，假設為θ，若則證明該柵格確實在活動區域內，然后通過下式

計算出具體位于哪個扇區(n表示第n個扇區，n＝0,1,2,.....,k)。最后對每個扇區的被障礙物占據的柵格個數做統計，若某個扇區的該數值大于0，則認為有障礙物占據，是不可行的；否則認為是可行的扇區。

(2d)考慮車寬對可行扇區進行篩選；

一般每個扇區對應的弧長只有0.42m左右，而車寬有2m，這意味著若車選擇了該扇區，雖然該扇區沒有障礙物，但鄰近扇區有障礙物依舊有可能產生碰撞，因此選擇扇區時應考慮車寬。根據計算可知，5個扇區對應的弧長大于2m，又由于車體的對稱性，選擇的可行扇區需滿足其左邊相鄰的兩個扇區與右邊相鄰的兩個扇區也是可行的。

(2e)用bezier曲線做為參考曲線選擇最優扇區；

經過(2d)步驟后，選出的滿足上述條件的扇區可能有多個，因此我們選擇用bezier曲線做為參考曲線選擇最優扇區。首先根據起始點和目標點的位姿以及軌跡最平滑準則選出一條最平滑的bezier曲線做為參考曲線，如圖6所示，具體過程可參照(1)中的步驟；由于每個扇區都對應一個軌跡點，對于每一個滿足(2d)條件的扇區，都可以通過其對應的軌跡點算出該點距離bezier曲線的最短距離(由于bezier曲線是用點集表示，計算最短距離時可先計算軌跡點距離曲線上每一個點的距離，然后在這些距離里取最短距離)。假設bezier曲線由n個點表示，滿足(2d)條件的扇區有m個，對于每一個扇區，可以計算出該扇區對于參考線的最短距離

di,min＝min{di,1,di,2,....,di,n},i＝1,2,...,m

其中，i表示第i個滿足(2d)條件的扇區，di,n表示第i個扇區對參考線上第n個點的距離，di,min表示第i個扇區距離參考線的最短距離。最后，我們可以通過公式

k＝argmin(di,min),k＝1,2,3,...,m

計算出哪個扇區是距離參考線最短，并認為該扇區是最優扇區，該扇區對應的軌跡點是最優軌跡點。

(2f)離散位置點集做控制點生成b樣條曲線；

由(2e)步驟得到的軌跡點屬于位置點集，無朝向角、速度等信息，而且點比較稀疏，無法做為車輛的可行軌跡。這里依據位置點集生成b樣條曲線的方式生成可行駛路徑。根據上述的b樣條數學模型，取n＝3，k＝3帶入公式(2-1)和(2-2)中得到三階b樣條曲線的基函數為：

現將位置點集做為b樣條曲線的控制點即可得到最終軌跡，該軌跡含有位置信息，航向角信息和曲率信息，可以做為無人駕駛車輛的可行路徑。

我們分別驗證了路口存在單障礙物以及多障礙物時該路徑規劃算法的有效性。實驗結果顯示，無人車在遇到障礙物時能夠有效避障并保持安全距離，繞過障礙物后在bezier曲線的約束下能夠按照期望的目標位姿回到目標點上，該算法實時有效。