基于正弦加速度函數的永磁球形電機點到點運動軌跡規劃方法及其應用與流程

本發明涉及三維空間中三自由度運動的軌跡規劃方法，具體的說是一種利用正弦加速度函數對永磁球形電機進行三維空間中點到點運動的軌跡規劃方法及其應用。
背景技術：
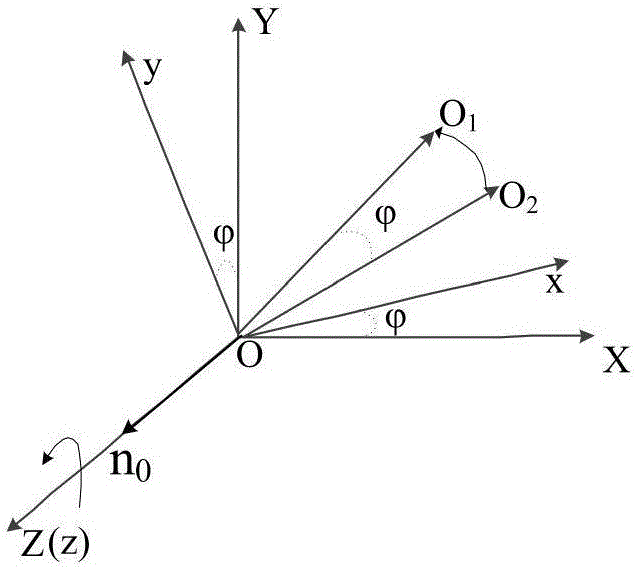
：隨著現代工業化和信息化水平的不斷發展，能夠實現多自由度運動的電機受到廣大學者的青睞。球形電機具有光明的應用前景，在機器人關節，機械手、全景攝像系統、衛星姿態控制系統等空間三維運動系統中，球形電機不僅能替代傳統組合電機完成三維空間的運動，而且能夠大大簡化其機構，提高控制精度，縮小體積，實現快速定位的目的。然而，由于球形電機運動學模型的強耦合特點，對其進行精確的控制比較復雜。目前，三維空間中軌跡規劃的相關研究工作多集中在多關節機器人或機械手上。針對球形電機的軌跡規劃主要討論轉子在笛卡爾空間中運動狀態的轉換與規劃，目前球形電機的軌跡研究大多集中在軌跡的精確跟蹤控制上，為獲得伺服任務預期的角位移、角速度及角加速度，需要大量的計算，控制規劃過程較為復雜。球形電機相關文獻中常見的軌跡大多是為了檢測控制系統的控制精度而給定的，沒有給出實際工況下運行所需的一般形式的軌跡規劃方法。對于空間中任意點到點運動的規劃求解更是少見，尤其是已知兩點坐標逆向求解歐拉旋轉角的方法上。有些是根據歐拉旋轉矩陣逆向求解歐拉旋轉角，有些是將轉子等效為四連桿機構利用四元數旋轉的方法求解，由于歐拉旋轉矩陣包含角位置信息且很難獲得，而四元數旋轉計算量大，而且有過多的約束條件限制，給實際的求解帶來諸多不便。同時，由于球形電機控制系統是個多輸入強耦合的控制系統，為了使電機精確穩定地運行，目前相關的研究工作多結合復雜智能控制算法對其進行精確跟蹤控制，這很有必要。但是，沒有考慮輸入信號可能對控制對象產生的不利影響。因此，目前急需一種簡單有效且易于控制的軌跡規劃方法技術實現要素：本發明為避免上述現有技術存在的不足之處，提出一種基于正弦加速度函數的永磁球形電機點到點運動軌跡規劃方法及其應用，以期能減少輸入信號的沖擊、不連續變化等因素對控制對象產生的不利影響，從而提高控制系統的控制精度和電機運行的穩定性。本發明為解決技術問題采用如下技術方案：本發明一種基于正弦加速度函數的永磁球形電機點到點運動軌跡規劃方法的特點是按如下步驟進行：步驟1：以永磁球形電機轉子為控制對象，分別建立定子靜坐標系O-XYZ和轉子動坐標系O-xyz，所述定子靜坐標系O-XYZ和轉子動坐標系O-xyz的原點O重合且固定在所述永磁球形電機轉子的中心位置上；以所述原點O作為球心，以所述球心O到所述永磁球形電機轉子的輸出軸頂點的距離R作為半徑，得到所述永磁球形電機轉子的運動軌跡球面；步驟2：若直接給定歐拉旋轉角，則執行步驟6；若給定所述定子靜坐標系O-XYZ下的兩點坐標，則執行步驟3；步驟3：判斷所述兩點坐標是否在所述運動軌跡球面上，若在運動軌跡球面上，則執行步驟4；否則，重新給定兩點坐標后，返回步驟2；步驟4：假設所述兩點坐標分別為A(x0,y0,z0)、B(x1,y1,z1)，則利用式(1)獲得法向量n：n＝(y0z1-y1z0,x1z0-x0z1,x0y1-x1y0)(1)步驟5：對所述法向量n進行分解后，利用式(2)獲得歐拉旋轉角θ(α,β,γ)：α=arcsin(y0z1-y1z0)β=arcsin(x1z0-x0z1)γ=arcsin(x0y1-x1y0)---(2)]]>步驟6：在給定所述永磁球形電機的運行時間T和初始角速度為0的條件下，利用式(3)得到所述永磁球形電機轉子的角加速度ω·=2πθT2sin(2πTt),t∈[0,T]---(3)]]>式(3)中，t表示時間變量；步驟7：利用式(4)獲得所述永磁球形電機轉子的轉矩τ：τ≈J·ω·---(4)]]>式(4)中，J表示所述永磁球形電機轉子的轉動慣量；步驟8：判斷時間變量t是否到達運行時間T，若到達，則所述永磁球形電機轉子根據所述轉矩τ完成永磁球形電機點到點的運動軌跡規劃，所述永磁球形電機的運行結束，否則返回步驟7。本發明一種基于正弦加速度函數的永磁球形電機點到點運動軌跡規劃方法的應用的特點是：應用于復雜連續軌跡的規劃，即利用插值法找出運動軌跡球面上復雜連續軌跡的若干關鍵點，再按照步驟3至步驟8求出相鄰兩個關鍵點的運動軌跡規劃，從而實現復雜連續軌跡的規劃。與已有技術相比，本發明的有益效果體現在：1、本發明永磁球形電機點到點運動軌跡規劃方法，不僅可以實現正向的旋轉運動，而且可以根據實際運行目標的需要，通過反向求解歐拉旋轉角，解析出點到點運動的歐拉旋轉角，然后規劃出簡單有效且易于控制的控制轉矩，從而實現了永磁球形電機點到點的基本運動。這種逆向求解歐拉旋轉角的方法，不僅適用于永磁球形電機，而且對于空間中剛體繞定軸轉動同樣適用，為實現空間中點到點的運動提供了有效的解決辦法。2、本發明永磁球形電機點到點運動軌跡規劃方法還可以應用于復雜連續軌跡的規劃，通過插值法得到連續軌跡上的若干關鍵點，再求出相鄰關鍵點的轉矩即可實現復雜連續軌跡的規劃。不僅能出色的完成簡單的點到點運動，而且能夠完成周期性以及復雜軌跡的運動，從而取代了結構復雜的多關節傳統組合電機，完成空間中的三自由度運動。3、本發明基于正弦加速度函數的軌跡規劃，比起矩形波或三角波函數，正弦函數具有表達式簡單、具有周期性等特點，能更有效減少由于控制輸入信號的沖擊、不連續變化等因素對電機轉子產生的擾動影響。同時，降低了控制轉矩的峰值，這對后續設計永磁球形電機驅動控制器至關重要。附圖說明圖1本發明永磁球形電機點到點運動軌跡規劃流程圖；圖2本發明定子靜坐標系O-XYZ和轉子動坐標系O-xyz及繞定軸z旋轉示意圖；圖3本發明空間任意點的繞定軸旋轉示意圖；圖4本發明三種方式下的角加速度曲線圖；圖5本發明三種方式下的角速度曲線圖；圖6本發明永磁球形電機轉子純傾斜運動軌跡圖；圖7a本發明三種方式下純傾斜運動Z軸轉矩曲線圖；圖7b本發明三種方式下純傾斜運動X軸位移曲線圖；圖7c本發明三種方式下純傾斜運動Y軸位移曲線圖；圖7d本發明三種方式下純傾斜運動Z軸位移曲線圖；圖7e本發明三種方式下純傾斜運動X軸角加速度曲線圖；圖7f本發明三種方式下純傾斜運動角速度曲線圖；圖8a本發明實施例1中類螺旋運動關鍵點圖；圖8b本發明實施例1中類螺旋運動仿真軌跡圖；圖9a本發明實施例2中安徽大學首字母AHU關鍵點圖；圖9b本發明實施例2中安徽大學首字母AHU仿真軌跡圖。具體實施方式本實施例中采用的是一臺三自由度的永磁球形電機，其外殼是一個球殼狀的定子，球形轉子安裝在球殼內，輸出軸固定在球形轉子上。轉子上沿赤道面對稱均勻分布四層永磁體，每層分別鑲嵌十個鐵釹硼材料的圓柱形永磁體，N、S級交替排列；定子上沿赤道面均勻鑲嵌兩層線圈，每層共有十二個圓柱型空芯線圈。通過實施本發明可以實現永磁球形電機轉子點到點的運功規劃。永磁球形電機繞定點旋轉的力學方程為：Jxωx·+(Jz-Jy)ωyωz=τx-τLxJyωy·+(Jx-Jz)ωxωz=τy-τLyJzωz·+(Jy-Jx)ωxωy=τz-τLz---(1)]]>式(1)即為永磁球形電機轉子動力學方程,Jx、Jy、Jz分別表示轉子x、y、z方向的轉動慣量，ωx、ωy、ωz分別表示轉子x、y、z方向的角速度，分別表示轉子x、y、z方向的角加速度，τx、τy、τz分別表示轉子x、y、z方向的控制轉矩，其中負載轉矩τLx、τLy、τLz也包含了摩擦轉矩引起的轉矩。由于永磁球形電機轉子的結構設計高度對稱，其三個方向的轉動慣量近似相等Jx＝Jz≈Jy＝J，表1記錄了永磁球形電機的轉動慣量，其中轉動慣量的單位為kg·m2。從式(1)可以看出，忽略摩擦引起的負載轉矩，轉矩與轉子的角加速度成正比，有：J·ω·≈τ--(2)]]>式中J、τ分別表示轉子轉動慣量、角加速度和控制轉矩矩陣，由式(2)可知，角加速度對轉矩的影響很大。因此，轉子從一點如何到達另一點的加速度規劃尤為重要。另外，在永磁球形電機通電控制策略的研究上，最終讓轉子運動的電磁轉矩與通電線圈的電流有直接的關系，電流越大，產生的電磁轉矩越大。因此，從能量的角度考慮，規劃出合理的角加速度也很有必要。表1永磁球形電機轉動慣量表(單位：kg·m2)本實施例中，一種基于正弦加速度函數的永磁球形電機點到點運動軌跡規劃方法，規劃過程如圖1所示，具體按如下步驟進行：步驟1：以永磁球形電機轉子為控制對象，分別建立定子靜坐標系O-XYZ和轉子動坐標系O-xyz，定子靜坐標系O-XYZ和轉子動坐標系O-xyz的原點O重合且固定在永磁球形電機轉子的中心位置上；以原點O作為球心，以球心O到永磁球形電機轉子的輸出軸頂點的距離R作為半徑，得到永磁球形電機轉子的運動軌跡球面；由歐拉旋轉定理可知，空間中任意兩點間的運動，都可以繞旋轉軸旋轉某一特定角來實現。這一過程同樣可以由歐拉旋轉的方式實現，通過分別控制x、y、z三個方向的控制轉矩，可以實現永磁球形電機三自由度運動的精確控制。步驟2：若直接給定歐拉旋轉角，則執行步驟6；若給定定子靜坐標系O-XYZ下的兩點坐標，則執行步驟3；對于永磁球形電機點到點的運動有兩種情況，一種是在歐拉旋轉角已知的情況下，通過旋轉相應的角度到達目標位置；另一種情況是已知起始點和終止點坐標，通過本發明中反向求解歐拉旋轉角的方法，求解出相應的歐拉旋轉角，從而完成相應的運動。步驟3：判斷兩點坐標是否在運動軌跡球面上，若在運動軌跡球面上，則執行步驟4；否則，重新給定兩點坐標后，返回步驟2；由于永磁球形電機的運動軌跡在球面x2+y2+z2＝R2上，所以給定兩點坐標必須在此球面上，否則無實際意義。步驟4：假設兩點坐標分別為A(x0,y0,z0)、B(x1,y1,z1)，則利用式(3)獲得法向量n：n＝(y0z1-y1z0,x1z0-x0z1,x0y1-x1y0)(3)步驟5：對法向量n進行分解后，利用式(4)獲得歐拉旋轉角θ(α,β,γ)：α=arcsin(y0z1-y1z0)β=arcsin(x1z0-x0z1)γ=arcsin(x0y1-x1y0)---(4)]]>反向求解歐拉旋轉角的具體求解推導方法如下：如圖2所示，在靜坐標系XOY平面內有一點O1(a,b,0)，繞z軸旋轉角度后到達點O2(c,d,0)，則可以看作繞向量OO1與OO2的法向量n0旋轉角度實現，設法向量n0為n0＝(nx0,ny0,nz0)，則有：n0＝OO1×OO2＝(nx0,ny0,nz0)＝(0,0,ac-bd)(5)注意到，即法向量n0不僅包含了旋轉軸，而且包含了旋轉角度的信息。將其擴展到三維空間中任意點的繞定軸轉動，如圖3所示，有空間中球面上任意點A(x0,y0,z0)，B(x1,y1,z1)。點A繞其法向量n＝(nx,ny,nz)旋轉φ角度后到達點B，這一過程可以通過分別繞x、y、z軸旋轉α、β、γ角度來實現。將法向量n分解到X、Y、Z三個方向得到nx、ny、nz，則上述旋轉過程可以看作繞nx、ny、nz分別旋轉α、β、γ角度實現。則有：n＝nx+ny+nz＝OA×OB＝(nx,ny,nz)＝(y0z1-y1z0,x1z0-x0z1,x0y1-x1y0)(8)φ=arccosx0x1+y0y1+z0z1x02+y02+z02x12+y12+z12---(9)]]>因此，可以得到式(4)中的歐拉旋轉角的表達式說明：若旋轉軸不是單位1，即給定點不是單位化后的坐標點，實際求解法向量過程需要將已知點的坐標單位化，文中給定的已知點的坐標是單位化后的坐標。任意點P(x,y,z)，單位化后的坐標Pe(xe,ye,ze)，則有Pe(xe,ye,ze)=1x2+y2+z2(x,y,z)---(10)]]>步驟6：常見的加速度函數有矩形波、三角波、正弦波、拋物線、指數函數等形式，在對比分析了三種形式簡單常用的矩形波、三角波、正弦波后，最終選擇了表達式簡單且易于控制的正弦波作為加速度函數。設運動周期為T，角位移為θ，角加速度為角速度為ω，從t＝0起始位置開始工作時間T，t＝T時到達終止位置，在給定永磁球形電機的運行時間T和初始角速度為0的條件下，利用式(11)得到永磁球形電機轉子的角加速度式(12)為永磁球形電機轉子的角速度表達式：ω·=2πθT2sin(2πTt),t∈[0,T]---(11)]]>ω=-θTcos(2πTt)+θT,t∈[0,T]---(12)]]>式(11)、(12)中t表示時間變量。圖4給出了相同周期相同角位移下的，矩形波、三角波、正弦波三種方式下的角加速度曲線圖，圖5給出了三種方式下的角速度曲線圖。表2記錄了純傾斜運動下，矩形波、三角波、正弦波三種常見加速度函數規劃下，角加速度最大值及轉矩最大值。可以得出，三種方式下，矩形波方式下所需最大轉矩最小、正弦波次之、三角波最大。所以，在時間和角位移相同的情況下，與三角波相比，矩形波所需的最大轉矩減少了約50％，正弦波減少了約21.46％。可見，加速度的方式不同，對控制轉矩的影響很大。結合圖3和圖4可以看出，加速度對時間的導數可表示加速度變化率，由式(2)可知，在永磁球形電機轉矩中，它表示轉矩的變化率。從三種方式下的角加速度波形可看出，矩形波雖然在前半周期和后半周期保持恒定，但在由正變負的瞬間，有很大的沖擊，這個沖擊會造成轉矩的擾動；而三角波顯然在峰值點處也不可導，即在該點處轉矩變化也不平滑；正弦波相比另外兩種波形，曲線變化平滑，數學表達式簡單、具有周期性、易于控制等優點，并且正弦波在電力輸送、變換等方面中已有廣泛的應用。因此，在點到點的運動方式下，以正弦函數作為加速度規劃函數是一種理想的選擇。表2三種方式下最大角加速度及最大轉矩表步驟7：利用式(13)獲得永磁球形電機轉子的轉矩τ：τ≈J·ω·---(13)]]>式(13)中，J表示永磁球形電機轉子的轉動慣量；說明：由永磁球形電機轉子的轉動慣量和解析出的角加速度函數，根據公式(13)得到控制轉矩，利用機械動力學仿真軟件Adams實現動力學仿真。首先，進行永磁球形電機虛擬樣機的轉子建模，添加質量、約束等屬性，完成三個方向的力矩添加；然后，校驗模型，設置運行時間和步長，進行仿真；最后，進入后處理界面，分析仿真結果。以純傾斜運動為例，設轉子輸出軸定點從初始位置P1(0,0.105,0)，經兩秒后到達點P2(-0.0617,0.085,0)，再經過兩秒后到達點P3(0.0617,0.085,0)，最后經過兩秒回到點P1。根據式(4)可以得到三次旋轉的歐拉角分別為θ1＝(0,0,0.6281)，θ2＝(0,0,-1.2577)，θ3＝(0,0,0.6281)。由式(11)可以得到每次旋轉相應x、y、z軸的角加速度函數，由于是沿X方向的純傾斜運動，故僅Z軸有角位移，所以僅對Z軸方向運動進行角加速度規劃，X、Y軸方向角加速度為零。三次旋轉的角加速度表達式分別為：a1z=0.3141·π·sin(π·t),t∈[0,2)a2z=-0.6289·π·sin(π·t),t∈[2,4)a3z=0.3141·π·sin(π·t),t∈[4,6]---(14)]]>對應的控制轉矩表達式分別為：τ1z=Jz·a1z=0.01483*0.3141·π·sin(π·t),t∈[0,2)τ2z=Jz·a2z=-0.01483*0.6289·π·sin(π·t),t∈[2,4)τ3z=Jz·a3z=0.01483*0.3141·π·sin(π·t),t∈[4,6]---(15)]]>具體在Adams軟件中進行動力學仿真時，可以用if函數來實現這種分段的表達式。對應轉矩的if函數表達式如下：τz=0.0148*if(time-2:0.3141*π*sin(π*time),0,if(time-4:-0.6289*π*sin(π*time),0,0.3141*π*sin(π*time)))---(16)]]>設置仿真時間為6秒，步長為300，仿真結束后，可以觀察后處理結果，進行仿真分析。表3記錄了純傾斜運動下仿真結果，X方向的最大角加速度(axmax)和Z方向的最大位移(Pzmax)，其中eax表示與矩形波相比X方向最大角加速度誤差，ePz表示與矩形波相比Z方向最大位移誤差。圖6是純傾斜運動下輸出軸頂點的運動軌跡圖，通過Adams軟件添加運動軌跡曲線獲得。結合圖7a可以看出，在周期相同、角位移相同的情況下，方式一所需控制轉矩最小，方式三次之，方式二最大，這與理論分析一致。圖7b和圖7c分別是三種方式下純傾斜運動X軸和Y軸的位移曲線，由于加速度方式的不同，X、Y方向的位移有微小的誤差。由于輸出軸沿X軸做純傾斜運動，故在Z軸方向位移應始終為零，且其在X軸的角加速度應始終為零。但從圖7d和圖7e可以看出，矩形波加速方式中，加速度由正變負的瞬間引起了波動，其中在t＝3s時，波動最大，而三角波加速方式中，在加速度曲線的峰值時刻，波動也較明顯，而在正弦波加速方式下，這種波動很小。圖7f是三種方式下純傾斜運動角速度曲線圖，可以看出，矩形波及三角波方式下，在加速度不連續變化時刻，對角速度的影響。從表3可以看出，與矩形波方式相比，三角波方式下的X軸最大加速度誤差減小了36.05％，正弦波方式下則減小了89.54％；三角波方式下的Z軸最大位移誤差比矩形波方式小了1.38％，正弦波方式下則減少了79.36％。另外，從加速度的表達式可以看出，正弦函數具有周期性，控制起來也較方便，驗證了加速度選擇為正弦函數的優越性。表3三種方式下X軸最大角加速度及Z軸位置誤差對比步驟8：判斷時間變量t是否到達運行時間T，若到達，則永磁球形電機轉子根據轉矩τ完成永磁球形電機點到點的運動軌跡規劃，永磁球形電機的運行結束，否則返回步驟7。一種利用基于正弦加速度函數的永磁球形電機點到點運動軌跡規劃方法的應用，將其應用于復雜連續軌跡的規劃，即利用插值法找出運動軌跡球面上復雜連續軌跡的若干關鍵點，再按照步驟3至步驟8求出相鄰兩個關鍵點的運動軌跡規劃，從而實現復雜連續軌跡的規劃。正弦函數ysin的一般表達式見式(17)，根據力的合成和分解可知，通過改變正弦函數的幅值Am和相位ψ，可以改變合力的大小和方向，從而得到復雜軌跡的控制轉矩，實現復雜軌跡的軌跡規劃。ysin＝Amsin(wt+ψ)+k(17)式(17)中w、k分別表示正弦函數的角頻率和位移參數。實施例1：類螺旋運動軌跡規劃如圖8a，選取球面上螺旋曲線A0-A6共7個關鍵點，轉子輸出軸頂端從起始點A0出發，依次到達A1、A2、A3、A4、A5、A6，其坐標如表4所示。根據式(4)求解求出相鄰兩點間的3個歐拉旋轉角，然后利用本發明提出基于正弦加速度函數的永磁球形電機軌跡規劃方法，規定每相鄰連點間運動時間為1秒，然后由式(11)求解出對應X、Y、Z方向的正弦加速度函數表達式，最后根據式(13)可得到控制轉矩的函數表達式。由于螺旋運動每一圈的運動類似一個圓，對力矩表達式稍作修改，由式(17)知，將正弦函數相位延時角度，幅值不變，即余弦函數形式。這樣，就得到了最終的控制轉矩函數，在Adams軟件中添加好轉矩，設定仿真時間，就可以得到類似螺旋的運動軌跡，如圖8b所示。表4類螺旋運動關鍵點實施例2：安徽大學首字母AHU軌跡的書寫如圖9a，選取球面上AHU字母的17個關鍵點，從起始點B0開始，依次經過B1-B16，最后回到起始點B0，根據式(4)求解求出相鄰兩點間的3個歐拉旋轉角，然后利用本發明提出基于正弦加速度函數的永磁球形電機軌跡規劃方法，規定每相鄰連點間運動時間為1秒，然后由式(11)求解出對應X、Y、Z方向的正弦加速度函數表達式，最后根據式(13)可得到控制轉矩的函數表達式。在Adams軟件用力矩采用if函數形式來表示，設置仿真時間為17秒，步長850，仿真運行后可得到其運動軌跡如圖9b所示。表5安徽大學首字母AHU關鍵點當前第1頁1 2 3