基于H∞次優濾波的角速度匹配傳遞對準方法與流程

本發明涉及一種空中飛行的對準方法，具體為基于h∞次優濾波的角速度匹配傳遞對準方法。

背景技術：

慣性導航系統的傳遞對準是低精度子慣導導航參數的初始化通過高精度主慣導的參數傳遞實現的，即傳遞對準。由于子慣導裝訂的初始值決定了后期慣性導航系統的導航精度，因此，傳遞對準是慣性導航系統傳遞對準的關鍵技術。理論上，主慣導與子慣導的陀螺都能感測到機體相對慣性空間的角速度，而且主慣導的陀螺輸出數值應該與不包括陀螺漂移的子慣導的陀螺輸出數值相同。

目前，主慣導都是采用高精度捷聯慣性導航系統，而捷聯慣性導航系統可以直接輸出載機的角速度。因此，采用角速度匹配傳遞對準就不需要計算載機的速度和姿態等導航參數，而是直接將載機的角速度經過處理后裝訂到子慣導系統中。但是在實際工程應用中，主慣導系統與子慣導系統之間，不僅存在常值安裝誤差角，而且還存在由于機翼彈性變形等因素引起的主子慣導之間的姿態失準角，主慣導提供給子慣導的信息需要進行一系列的濾波處理之后才能作為子慣導的初始信息。

角速度匹配傳遞對準的量測量是主慣導的高精度陀螺測量信息與子慣導的陀螺測量信息之差，將角速度匹配傳遞對準的量測量送入卡爾曼濾波器進行信息融合，以獲得導航系統誤差的最優估計值。目前，傳遞對準中常用的最優估計方法是卡爾曼濾波，卡爾曼濾波要求知道準確的干擾信號統計特性以及系統動力學模型。如果狀態變量可觀測，則狀態變量的估計值會逐漸收斂；而對于不可觀測的狀態變量，卡爾曼濾波就會發散，無法將狀態變量估計出來的。

實際應用中，慣性導航系統的工作環境非常惡劣，角速度匹配傳遞對準過程中的干擾信號是隨機信號，很難得到干擾信號精確的統計特性，而且很多情況下系統模型本身也存在一定范圍的變化，僅僅通過調整卡爾曼濾波器的相關參數提高子慣導對準性能是很有限的。因此需要在傳遞對準中尋求一種新的信息融合技術。

技術實現要素：

針對現有技術中存在的問題，本發明提供一種基于h∞次優濾波的角速度匹配傳遞對準方法，魯棒性好，能夠在系統噪聲與量測噪聲未知或不完全可知的情況下，能獲得比傳統卡爾曼濾波更好的估計精度。

本發明是通過以下技術方案來實現：

基于h∞次優濾波的角速度匹配傳遞對準方法，包括如下步驟，

步驟1，構建角速度匹配傳遞對準的系統狀態空間模型；所述系統狀態空間模型的狀態變量包括子慣導安裝誤差角、機翼撓曲變形角、機翼撓曲變形角速度和子慣導陀螺的常值漂移；

步驟2，以主慣導提供的角速度為量測量的參考信息，構建角速度匹配傳遞對準的量測模型；

步驟3，在干擾項為有色噪聲時，通過h∞次優濾波算法利用量測模型中的量測量對角速度匹配傳遞對準的系統狀態空間模型中系統狀態量的線性組合進行誤差的最優估計，得到子慣導的安裝誤差角與姿態失準角，實現基于h∞次優濾波的角速度匹配傳遞對準。

優選的，步驟1中，所述的角速度匹配傳遞對準的系統狀態空間模型如下，

其中，角速度匹配傳遞對準的系統狀態為為子慣導安裝誤差角，λf為機翼撓曲變形角，ωf為機翼撓曲變形角速度，為子慣導陀螺的常值漂移，η為二階撓曲白噪聲驅動，β為機翼彈性阻尼系統的自振頻率。

優選的，所述的角速度匹配傳遞對準的系統狀態空間模型由如下的角速度匹配傳遞對準的系統狀態方程得到，

優選的，步驟2中，所述的角速度匹配傳遞對準的量測模型如下，

其中，為主慣導角速度真值，為已知的子慣導安裝矩陣，vω為角速度匹配量測噪聲，xω為角速度匹配傳遞對準的系統狀態。

優選的，所述的已知的子慣導安裝矩陣如下，

其中，θs為子慣導安裝于載機機翼下方并繞縱軸相對水平位置轉過的角度。

優選的，所述的角速度匹配傳遞對準的量測模型由如下的角速度匹配傳遞對準的量測量方程得到，

其中，為子慣導角速度真值，為子慣導陀螺的常值漂移，為量測白噪聲。

優選的，步驟3中，利用h∞次優濾波算法對角速度匹配傳遞對準的系統狀態空間模型和量測模型進行誤差的最優估計，具體包括如下步驟，

步驟3.1，對狀態空間模型和量測模型作離散化處理后得到線性離散系統的系統方程與量測方程為：

其中，xk為系統狀態量，zk為系統量測量，φk,k-1為tk-1時刻到tk時刻的一步轉移矩陣，hk為系統量測矩陣，γk-1為系統干擾輸入矩陣，wk-1為系統激勵噪聲，vk為量測噪聲，下標k表示是在k時刻的各參數量，k-1表示k時刻的前一刻的各參數量；

步驟3.2，利用系統量測量對系統狀態量的線性組合估計，對sk＝lkxk中的系統量測量函數sk進行估計，其中，lk為系統狀態量給定的線性變換矩陣；

假定為利用從0時刻到k時刻的量測向量對sk的估計，那么估計誤差就可以描述為：

步驟3.3，對h∞次優濾波進行定義；給定一個常數γ＞0，并確定h∞次優估計使得||tk(f)||∞＜γ成立，即

其中，x0為系統初始狀態，為對x0的估計，為系統的初始狀態誤差；p0為反映x0的初始假設與真實值x0接近程度的正定矩陣，且tk(f)為傳遞函數矩陣；

步驟3.4，針對步驟3.1中描述的線性離散系統，給定常數γ＞0，如果矩陣[φkγk]行滿秩，則步驟3.3中h∞次優濾波問題存在解的充分必要條件為，

且h∞次優濾波的解，即h∞次優濾波估計的遞推方程如下，

傳遞對準過程中lk＝i；

其中，為(k+1)時刻的系統狀態估計，為k時刻的系統狀態估計，φk為一步轉移矩陣，φk,k-1為tk-1時刻到tk時刻的狀態轉移矩陣，kk+1為表示卡爾曼增益，是濾波的中間結果，zk+1為(k+1)時刻的系統量測量，hk+1為(k+1)時刻的系統量測矩陣，pk+1為(k+1)時刻的估計誤差的方差陣，γk為k時刻的系統干擾輸入矩陣；

步驟3.5，根據h∞次優濾波輸出的(k+1)時刻的系統狀態估計得到子慣導的安裝誤差角與姿態失準角，實現基于h∞次優濾波的角速度匹配傳遞對準。

與現有技術相比，本發明具有以下有益的技術效果：

在實際的飛行過程中，由于受到外界環境等因素的影響，子慣導在使用載機傳遞的相關參數裝訂初始值時受到干擾角速度與機翼彈性變形等隨機信號的影響。本發明通過對角速度匹配傳遞對準的系統狀態模型和量程模型的構建和分析，在將機翼彈性變形等干擾項為有色噪聲時，針對系統動態模型的和噪聲的統計特性無法完全獲得的情況下，傳統的卡爾曼濾波存在計算量大，實時性差以及容錯性能低等缺點。本發明將h∞次優濾波應用到角速度匹配傳遞對準中，能夠快速估計出彈體的安裝誤差角與姿態失準角，從而實現慣性導航系統的快速傳遞對準。后續工作將繼續采用參數估計的方法，結合模糊自適應濾波理論對卡爾曼濾波進行一定的改進，對角速度匹配傳遞對準的方法進行優化提升。克服了現有的卡爾曼濾波對于隨機信號的抑制性能較差，甚至出現發散的情況問題和缺陷。

附圖說明

圖1為本發明實例中所述角速度匹配傳遞對準方法的原理框圖。

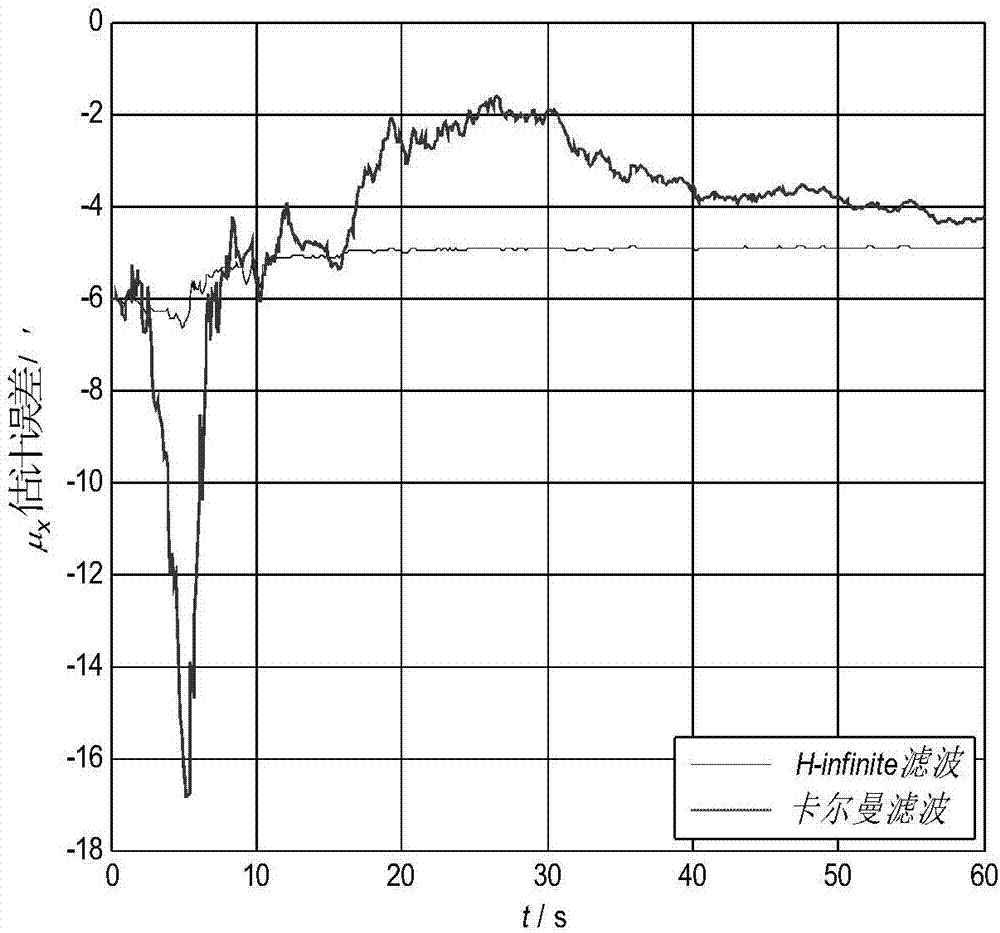
圖2a為本發明實例中所述角速度匹配安裝誤差角μx估計誤差。

圖2b為本發明實例中所述角速度匹配安裝誤差角μy估計誤差。

圖2c為本發明實例中所述角速度匹配安裝誤差角μz估計誤差。

圖3a為本發明實例中所述角速度傳遞對準失準角估計誤差。

圖3b為本發明實例中所述角速度傳遞對準失準角估計誤差。

圖3c為本發明實例中所述角速度傳遞對準失準角估計誤差。

具體實施方式

下面結合具體的實施例對本發明做進一步的詳細說明，所述是對本發明的解釋而不是限定。

本發明通過對角速度匹配傳遞對準的系統狀態模型和量程模型的構建與分析，在將機翼彈性變形等干擾項為有色噪聲時，采用h∞次優濾波的角速度匹配傳遞對準方式估計彈體的安裝誤差角與姿態失準角，從而實現慣性導航系統的快速傳遞對準。

現有技術中，角速度匹配傳遞對準是將主慣導與子慣導的陀螺測量信息之差作為觀測量，傳遞對準過程中，采用卡爾曼濾波算法對子慣導的安裝誤差角及機翼彈性變形進行估計，待估計達到要求的精度后，再對姿態陣做一次性修正。

本發明中設主慣導的陀螺輸出為子慣導的陀螺輸出為子慣導安裝誤差角為機翼撓曲變形角為λf。角速度匹配傳遞對準原理圖如圖1所示。

首先，構建角速度匹配傳遞對準的系統狀態空間模型。

系統狀態空間模型的建立關鍵是狀態變量的選取，根據這些狀態變量列寫出子慣導基本誤差方程。子慣導的輸出與參考系統的相應輸出作比較再構造量測量，則在這些量測量中包含有初始誤差的信息。

設角速度匹配傳遞對準的系統狀態為其中，子慣導安裝誤差角機翼撓曲變形角λf＝[λfxλfyλfz]^t。機翼撓曲變形角速度ωf＝[ωfxωfyωfz]^t，子慣導陀螺的常值漂移則角速度匹配傳遞對準的系統狀態方程為：

由此可得角速度匹配傳遞對準的系統狀態空間模型為：

其中，η＝[ηxηyηz]^t為二階撓曲白噪聲驅動，η為零均值均勻分布，即ηi～n(0,qi)，為三個彈性變形角的方差強度；β為機翼彈性阻尼系統的自振頻率，并且滿足[β]＝diag(βx,βy,βz)，

其次，構建角速度匹配傳遞對準的量測模型。

為了合理設計h∞次優濾波器實現傳遞對準，必須選用外部參考信息來構造量測量。量測量都是在有限的時間間隔內得到的，利用這個時間間隔內的所有量測量來估計系統在這個時間段內整個過程的狀態變量。

已知為主慣導的陀螺輸出，為子慣導的陀螺輸出，為已知的子慣導安裝矩陣。假設子慣導安裝于載機機翼下方并繞縱軸相對水平位置轉過θs角，可知子慣導的常值安裝矩陣為：

由于主慣導使用的陀螺的精度一般都比子慣導陀螺精度高2～3個數量級，而且主慣導會與gps組合以便抑制主慣導的誤差發散。因此將主慣導陀螺輸出的角速度視為角速度的真值。主慣導與子慣導的陀螺儀輸出分別為：

其中，主慣導角速度和子慣導角速度真值分別為子慣導陀螺的常值漂移為量測白噪聲為

則角速度匹配傳遞對準的量測量為：

若機翼彈性變形角為λ＝λf+λv，λf為機翼撓曲變形角，λv為機翼顫振變形角；機翼彈性變形角速度為ωλ＝ωf+ωv，其中ωf為撓曲變形角速度，ωv為顫振變形角速度。則有：

將式(9)帶入式(8)可得：

其中，vω為角速度匹配量測噪聲，且有：

由此可得角速度匹配傳遞對準的量測模型為：

最后，利用h∞次優濾波算法。

h∞次優濾波是針對干擾信號和系統模型的不確定性，構建濾波器使得從干擾信號輸入到誤差輸出的閉環傳遞函數的范數小于某一給定的正數。通常情況下，h∞次優濾波需要利用系統量測量對系統狀態量的線性組合進行估計。

實際的物理系統一般都是連續的，動力學特性用連續微分方程描述。但是h∞次優濾波基本方程適用于系統方程和量測方程都是離散型的情況，所以使用基本方程之前，必須對狀態空間模型和量測模型作離散化處理。

設線性離散系統的系統方程與量測方程為：

其中，xk為系統狀態量，zk為系統量測量，φk,k-1為tk-1時刻到tk時刻的一步轉移矩陣，hk為系統量測矩陣，γk-1為系統干擾輸入矩陣，wk-1為系統激勵噪聲，vk為量測噪聲，下標k表示是在k時刻的各參數量，k-1表示k時刻的前一刻的各參數量。

系統量測量對系統狀態量的線性組合估計，即對下式中的系統量測量函數sk進行估計：

sk＝lkxk(2)

其中，lk為系統狀態量給定的線性變換矩陣。

假定為利用從0時刻到k時刻的量測向量對sk的估計，那么估計誤差就可以描述為：

定義(h∞次優濾波)：給定一個常數γ＞0，并確定h∞次優估計使得||tk(f)||∞＜γ成立，即

其中，x0為系統初始狀態，為對x0的估計，為系統的初始狀態誤差；p0為反映x0的初始假設與真實值x0接近程度的正定矩陣，且tk(f)為傳遞函數矩陣。

針對(1)式所描述的線性離散系統，給定常數γ＞0，如果矩陣[φkγk]行滿秩，則(4)式的h∞次優濾波問題存在解的充分必要條件為：

且h∞次優濾波的解，即h∞次優濾波估計的遞推方程為：

傳遞對準過程中lk＝i。

其中，為(k+1)時刻的系統狀態估計，為k時刻的系統狀態估計，φk為一步轉移矩陣，φk,k-1為tk-1時刻到tk時刻的狀態轉移矩陣，kk+1為表示卡爾曼增益，是濾波的中間結果，zk+1為(k+1)時刻的系統量測量，hk+1為(k+1)時刻的系統量測矩陣，pk+1為(k+1)時刻的估計誤差的方差陣，γk為k時刻的系統干擾輸入矩陣。

根據h∞次優濾波輸出的(k+1)時刻的系統狀態估計得到子慣導的安裝誤差角與姿態失準角，實現基于h∞次優濾波的角速度匹配傳遞對準。

傳統的傳遞對準中廣泛的采用卡爾曼濾波技術。但是在傳遞對準模型存在誤差和噪聲特性時變的情況下，僅僅通過調整卡爾曼濾波器的相關參數提高子慣導對準性能是很有限的，因此需要探討新的信息融合技術在傳遞對準中的應用。h∞濾波技術是比較有前景的信息融合技術，在系統噪聲與量測噪聲的未知或不完全可知的情況下，能獲得比卡爾曼濾波更好的估計精度。h∞次優濾波具有速度快、精度高、魯棒性好的特點，而且更符合工程應用的實際情況。

將本發明所述的方法和現有技術中的卡爾曼濾波進行角速度匹配傳遞對準的仿真分析對比如下。

角速度匹配傳遞對準中需要對子慣導的安裝誤差角及機翼彈性變形進行估計，然后再對姿態失準角進行修正。由傳遞對準基本匹配方法的分析可以知道，姿態匹配與角速度匹配對機翼彈性變形都非常敏感，當機翼彈性變形建模不準時，會導致角速度匹配傳遞對準的卡爾曼濾波性能惡化,對準性能降低，嚴重時可能導致濾波器發散。

為切合實際工程應用，本文的角速度匹配傳遞對準仿真中，假設在傳遞對準開始前主慣導有gps等導航系統輔助，而傳遞對準過程中主慣導工作在純慣性導航系統狀態。同時濾波時不對機翼彈性變形進行建模，而是將其看作隨機信號，因此角速度匹配傳遞對準的量測量里包含未知的量測噪聲。由于角速度匹配傳遞對準對機翼撓曲變形很敏感，采用角速度匹配方案進行傳遞對準時，盡量將子慣導掛在機翼根部或機腹下，以降低機翼撓曲變形及顫振對角速度匹配傳遞對準的影響。

仿真條件：角速度匹配傳遞對準中載機的機動采用搖翼機動。假設搖翼仿真總時間為12s，搖翼角度為30°；傳遞對準初始位置為北緯34.03006°、東經108.76405°，海拔高度480m；飛機的飛行速度為230m/s；飛行高度為7000m；航向角為60°，俯仰角為0°，橫滾角為0°。傳遞對準搖翼仿真運動軌跡設計如表1所示。

表1仿真軌跡設計

子慣導誤差參數：陀螺常值漂移：1°/h；

陀螺隨機游走系數：

加速度計常值偏置誤差：5×10^-4g；

加速度計量測白噪聲標準差：

子慣導安裝誤差角：

裝訂引起的子慣導失準角初值：

子慣導速度誤差初值：

仿真時濾波周期取為20ms，并且取γ＝50，仿真結果如圖2a、圖2b、圖2c與圖3a、圖3b、圖3c所示，圖中實線為h∞次優濾波仿真結果，點劃線為卡爾曼濾波仿真結果。能夠得到如下結論。

1)根據角速度匹配傳遞對準原理及慣導誤差傳播方程，子慣導的安裝誤差角是通過載機轉動角速度對其的耦合影響來體現的。由于仿真過程中載機采用搖翼機動，只是在y軸方向有角速度輸出，因此只能對子慣導的x軸和z軸安裝誤差角進行有效估計，如圖2a和圖2c所示；而且由于y軸與當地地理北向重合，因此無法正確估計出彈體的北向失準角，如圖3b所示北向失準角是發散的。

2)當系統噪聲與量測噪聲為有色噪聲而且存在建模誤差時，卡爾曼濾波收斂速度明顯低于h∞次優濾波的收斂速度。如圖3a和圖3c所示，h∞次優濾波在15s時東向和天向的失準角已經收斂在10'以內，而卡爾曼濾波在30s左右時才收斂到10'以內。

仿真結果表明，將h∞次優濾波應用于角速度匹配傳遞對準中，尤其對提高經常受到機翼彈性變形等不確定性擾動影響的子慣導的初始值精度效果明顯。基于h∞次優濾波的角速度匹配傳遞對準方案，能有效抑制實際工程應用中子慣導的機翼彈性變形等外界不確定噪聲的干擾，在確保慣導系統魯棒性能的同時，可以獲得良好的快速性和較好的濾波精度。因此，作為一種空中飛行的對準方法，采用h∞濾波將干擾項作為有色噪聲應用于角速度匹配傳遞對準更符合工程應用的實際情況。