一種彈載地磁姿態測量處理算法的制作方法

本發明屬于地磁導航應用技術領域，具體地說，涉及一種彈載地磁姿態測量處理算法。

背景技術：

地磁場是地球系統的基本物理場，是地球的固有資源，為航空、航天、航海提供了天然的參考系，可應用于航天器或艦船的定位定向及姿態控制。利用地球磁場空間分布的磁導航技術簡便高效、性能可靠、抗干擾，一直是世界發達國家不可缺少的基本導航定位手段，如自動化程度很高的波音飛機都裝載有磁導航定位系統。當前，地磁技術已廣泛應用于地球科學、資源探測、航天航空、交通通訊、地震預測、空間天氣、測繪等諸多領域，擁有巨大的應用潛力。

地球磁場同地球引力場一樣，是一個地球物理場，它是由基本磁場與變化磁場兩部分組成的。基本磁場來源于地球內部，研究它的變化及其起源，一直是地球動力學中的重要內容之一，而變化磁場則與電離層的變化和太陽活動等有關。地磁場是由不同來源的磁場疊加起來構成的，按其來源可把地磁場分為兩大部分：一部分為穩定磁場，另一部分主要是起源于地球外部的快速變化磁場。快速變化磁場比穩定磁場弱的多，最大變化也只占總磁場的2％-4％。因此穩定磁場是地磁場的主要部分。地球主磁場的變化極為緩慢，這種變化稱為地磁場的長周期變化。地球的變化磁場則是起源于外部并疊加在主磁場之上的各種短周期的地磁場變化。地球基本磁場變化十分緩慢，年變率在千分之一以下。外源場變化的時間尺寸比較小，變化比較復雜，平靜時的外源場的強度不到內源場的千分之一，強擾動時的外源場也在內源場的百分之一以下。因此，在考慮地磁場本身對航天器的影響時，只需考慮內源場中的基本磁場。

炮彈的空中姿態測量，特別是高過載下姿態測量在國內仍是一大技術難題,很多方法尚處于探索中。

技術實現要素：

本發明的目的在于克服炮彈的空中姿態測量技術存在的缺陷，提供一種彈載地磁姿態測量處理算法。

其具體技術方案為：

一種彈載地磁姿態測量處理算法，包括以下步驟：彈載雙軸地磁傳感器固定與彈體上，與彈軸方向垂直，敏感Y、Z方向的磁阻變化，

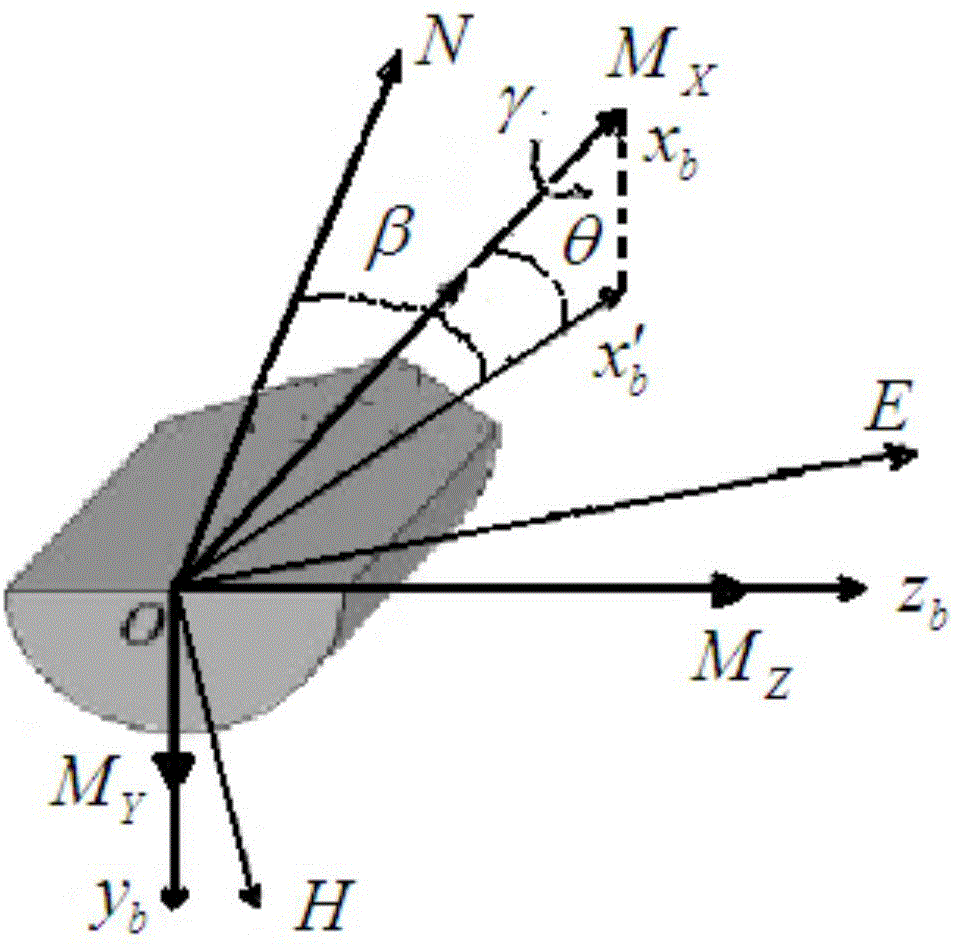
以北東天導航坐標系為參考，x′_b為x_b在NOE平面上的投影，γ為彈體滾轉姿態角，β為偏航角，θ為俯仰角。根據坐標變換，得到彈體Y、Z方向的地磁輸出：

式中ψ＝D+β為彈體的磁偏航角(磁射向)，φ＝θ+I為彈體的磁俯仰角。

根據發射陣地地和飛行過程中的經緯度和高度信息可以計算出任意飛行彈道點上的地磁偏角D和地磁傾角I；

根據飛行中衛星定位裝置探測的速度信息：V_N、V_E、V_H和彈道運動方程組可以初步計算出彈丸彈道傾角θc和速度航向角βc，根據炮彈姿態角轉換關系：β＝β_C+δ₂和θ＝θ_C+δ₁，δ₁、δ₂為炮彈攻角分量，可忽略不計。

從公式(1)可知，根據計算出炮彈飛行彈道上磁偏航角ψ和磁俯仰角φ要解出滾轉姿態角γ，需要制導地磁場矢量的大小|M|。分析(1)可以看出，當M_Y＝0和M_Z＝0時，解算出滾轉姿態角γ不需要|M|。由于滾轉姿態角γ∈[0°,360°]，所以無論磁俯仰角φ在哪個范圍，在一個旋轉周期內必有M_Y＝0和M_Z＝0的點。根據磁偏航角ψ的取值范圍，分析滾轉姿態角γ的解算方法：

1)當磁偏航角ψ＝0°或磁偏航角ψ＝180°時：

當M_Y＝0時，如果sinφ≠0，則cosγ＝0,此時滾轉姿態角γ＝90°或γ＝-90°。

當M_Z＝0時，如果sinφ≠0，則sinγ＝0,此時滾轉姿態角γ＝0°或γ＝180°。

對于遠程打擊的滑翔增程炮彈，全飛行過程中磁俯仰角φ只可能在彈道頂點某點上sinφ＝0，滑翔增程和精度控制是過彈道頂點后才開始控制的。

2)當磁偏航角ψ≠0°或磁偏航角ψ≠180°時：

當地磁傳感器的輸出M_Y＝0時，可得到下式：

|M|sinγsinψcosφ+|M|cosγsinφ＝0

|M|≠0，可得:

當地磁傳感器的輸出M_Z＝0時，可得到下式：

|M|sinγsinφ-|M|cosγsinψcosφ＝0

|M|≠0，可得:

根據計算出炮彈飛行彈道上任意點的磁偏航角ψ和磁俯仰角φ，由(3)、(4)可以解算出M_Y＝0和M_Z＝0極值點＝相對應的出滾轉姿態角γ_E0和γ_H0。從計算公式看，γ_E0和γ_H0相差90°。

若以彈體上地磁傳感器的輸出M_Z＝0與舵控正方向標定滾轉角，則M_Z＝0時滾轉姿態角γ(γ_H0)隨磁偏航角ψ和磁俯仰角φ的變化關系可得：

γ_H0＝arctan(sinψ.tanφ) (5)

由(5)式可實時計算出炮彈飛行過程中M_Z＝0時炮彈的滾轉姿態角，根據計算的轉速，可積分計算出任意點出的滾轉姿態角γ：

與現有技術相比，本發明的有益效果：

本發明提供一種彈載地磁姿態測量處理算法在驗證過程中，磁探測基準理論計算值與射角變化檢測值的對比曲線，從幾種檢測結果看，理論計算值與實際檢測值基本一致，最大偏差范圍：-3.2°～+2.97°。

附圖說明

圖1是磁傳感器安裝示意圖。

具體實施方式

下面結合附圖和具體實施方案對本發明的技術方案作進一步詳細地說明。

一種彈載地磁姿態測量處理算法，包括以下步驟：彈載雙軸地磁傳感器固定與彈體上，與彈軸方向垂直，敏感Y、Z方向的磁阻變化，具體安裝急與彈體坐標關系如圖1所示。

以北東天導航坐標系為參考，x′_b為x_b在NOE平面上的投影，γ為彈體滾轉姿態角，β為偏航角(射向)，θ為俯仰角(射角)。根據坐標變換，得到彈體Y、Z方向的地磁輸出：

式中ψ＝D+β為彈體的磁偏航角(磁射向)，φ＝θ+I為彈體的磁俯仰角(磁射角)。

根據發射陣地地和飛行過程中的經緯度和高度信息可以計算出任意飛行彈道點上的地磁偏角D和地磁傾角I；

根據飛行中衛星定位裝置探測的速度信息：V_N、V_E、V_H和彈道運動方程組可以初步計算出彈丸彈道傾角θc和速度航向角βc，根據炮彈姿態角轉換關系：β＝β_C+δ₂和θ＝θ_C+δ₁，δ₁、δ₂為炮彈攻角分量，可忽略不計。

從公式(1)可知，根據計算出炮彈飛行彈道上磁偏航角ψ和磁俯仰角φ要解出滾轉姿態角γ，需要制導地磁場矢量的大小|M|。分析(1)可以看出，當M_Y＝0和M_Z＝0時，解算出滾轉姿態角γ不需要|M|。由于滾轉姿態角γ∈[0°,360°]，所以無論磁俯仰角φ在哪個范圍，在一個旋轉周期內必有M_Y＝0和M_Z＝0的點。根據磁偏航角ψ的取值范圍，分析滾轉姿態角γ的解算方法：

1)當磁偏航角ψ＝0°或磁偏航角ψ＝180°時：

當M_Y＝0時，如果sinφ≠0，則cosγ＝0,此時滾轉姿態角γ＝90°或γ＝-90°。

當M_Z＝0時，如果sinφ≠0，則sinγ＝0,此時滾轉姿態角γ＝0°或γ＝180°。

對于遠程打擊的滑翔增程炮彈，全飛行過程中磁俯仰角φ只可能在彈道頂點某點上sinφ＝0，滑翔增程和精度控制是過彈道頂點后才開始控制的。

2)當磁偏航角ψ≠0°或磁偏航角ψ≠180°時：

當地磁傳感器的輸出M_Y＝0時，可得到下式：

|M|sinγsinψcosφ+|M|cosγsinφ＝0

|M|≠0，可得:

當地磁傳感器的輸出M_Z＝0時，可得到下式：

|M|sinγsinφ-|M|cosγsinψcosφ＝0

|M|≠0，可得:

根據計算出炮彈飛行彈道上任意點的磁偏航角ψ和磁俯仰角φ，由(3)、(4)可以解算出M_Y＝0和M_Z＝0極值點＝相對應的出滾轉姿態角γ_E0和γ_H0。從計算公式看，γ_E0和γ_H0相差90°。

若以彈體上地磁傳感器的輸出M_Z＝0與舵控正方向(鉛直向上)標定滾轉角，則M_Z＝0時滾轉姿態角γ(γ_H0)隨磁偏航角ψ和磁俯仰角φ的變化關系可得：

γ_H0＝arctan(sinψ.tanφ) (5)

由(5)式可實時計算出炮彈飛行過程中M_Z＝0時炮彈的滾轉姿態角，根據計算的轉速，可積分計算出任意點出的滾轉姿態角γ：

以上所述，僅為本發明較佳的具體實施方式，本發明的保護范圍不限于此，任何熟悉本技術領域的技術人員在本發明披露的技術范圍內，可顯而易見地得到的技術方案的簡單變化或等效替換均落入本發明的保護范圍內。