基于生成多項式庫搜索匹配算法的Gold序列參數估計方法與流程
本發明涉及一種含誤碼gold序列的生成多項式及初始狀態的估計,適用于擴頻通信、雷達測距、碼分多址系統等領域中的偽隨機序列的生成多項式及初始狀態的估計。
背景技術:
偽隨機序列在擴頻通信、雷達測距、碼分多址系統以及密碼學等領域都有著廣泛的應用。若使用隨機序列進行相關檢測,在接收端不能產生與發送端完全相同的隨機序列,因此在實際應用中,廣泛采用按照一定規律產生的偽隨機序列。使用最多的是m序列和gold序列,都可以使用線性反饋移位寄存器產生,具有實現簡單、偽隨機特性好及相關性好的優點。
m序列是最大周期線性反饋移位寄存器序列,是目前理論研究比較成熟、應用較為廣泛的一種偽隨機序列。m序列具有良好的平衡性、平移相加性和二值自相關性,但一定長度的m序列個數較少。相比于m序列,而gold序列(包括m序列)在保持m序列的優良性質的情況下擴展了m序列的數量,可以用于擴頻碼的數量較多因此被廣泛應用于現代通信技術中。
gold序列是基于m序列優選對產生的。在m序列集中,互相關函數的絕對值小于某個值的兩個m序列被稱為m序列優選對。在gold序列族中,既包括生成該gold序列的m序列的m序列優選對,也包括兩者移位模二加后產生的新序列。gold序列的參數包括生成多項式、構成該gold序列的m序列優選對的本原多項式和初始狀態,是完成擴頻序列恢復和信息解密的基礎。
技術實現要素:
本發明所要解決的技術問題是,目前對gold序列參數估計得研究甚少,且未對構造gold序列的兩個m序列初始狀態進行估計。gold序列的參數估計問題是信息解擾和信號干擾的重要研究環節,因此gold序列的參數估計具有重要的研究價值。
本發明解決上述問題的技術方案是,為解決gold序列參數估計問題,提出了一種基于生成多項式庫搜索匹配算法的參數估計方法。
本發明提出的gold序列參數估計方法,包括如下步驟:
步驟1:截取長度為l的部分含誤碼n階gold序列。
步驟2:按照gold序列的階數n構造關于生成多項式的方程組,在gold序列生成多項式庫中進行搜索匹配,若出現方程組右邊為零的方程個數大于閾值的多項式就是gold序列的生成多項式,構造該生成多項式的兩個本原多項式就是兩個m序列優選對的本原多項式ma(x)和mb(x)。
步驟3:先固定ma(x)和mb(x)的初始狀態為[0001]。對ma(x)生成的序列循環移位i=0次,對mb(x)生成的序列循環移位j=0次。
步驟4:有這兩個序列進行模2加后與原序列進行對比,若對應位置相同的概率大于80%,算法結束,否則若j<2n-2,則j=j+1,繼續執行步驟2。若j=2n-2,則i=i+1,繼續執行步驟2.
ma(x)初始狀態為循環移位i次后的前n項,mb(x)初始狀態為循環移位i次后的前n項。
本發明提供的gold序列參數估計方法在截取序列長度較短的情況下,能較好地估計出gold序列的參數且有一定的容錯性。
附圖說明
圖1gold序列生成原理圖
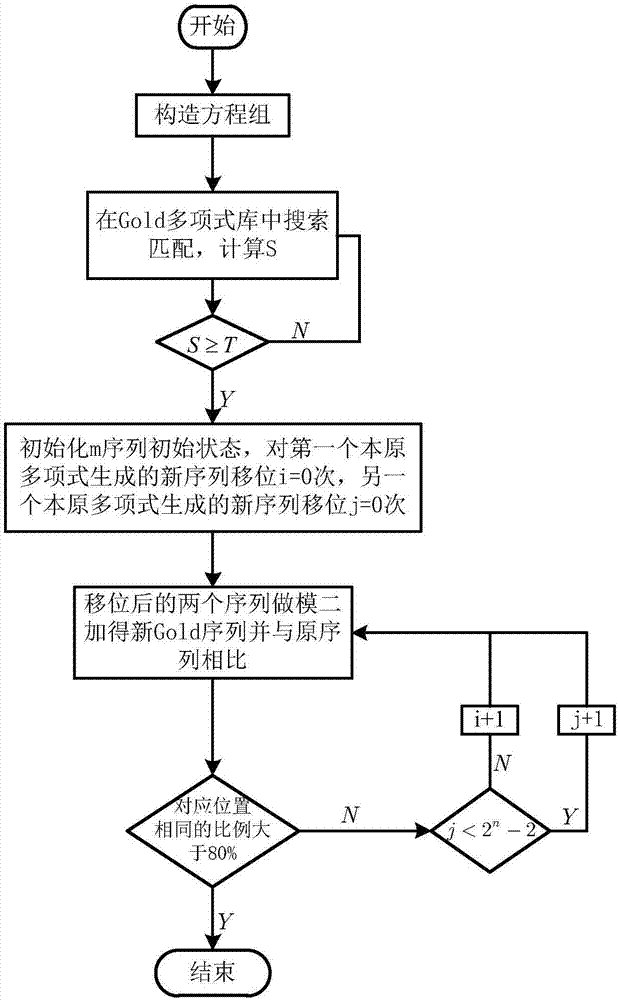
圖2含誤碼gold序列參數估計流程圖
圖313階gold序列生成多項式估計結果圖
圖4不同階數gold序列容錯性對比圖
具體實施方式
偽隨機序列有如下形式:
ai=cnai-n+…+cvai-v+…+c1ai-1(1)
集合{ai}=a0,a1,a2,…中的元素可以由遞推公式計算得到
則有:
clai-l+cl-1ai-l+1+…+cvai-v+…+ai=0(3)
其中n為序列生成多項式的階數。本發明研究對象為二進制偽隨機序列,因此式中元素ai,ci∈gf(2)。偽隨機序列的線性遞推關系說明其具有嚴格的線性約束關系,這是本發明參數估計方法的基礎。
gold序列是兩個m序列優選對循環移位疊加構造得到的偽隨機序列。其周期為n=2n-1,n是m序列優選對的階數,生成多項式的階數為2n。此時gold序列的生成多項式為
g(x)=c2nx2n+c2n-1x2n-1+…+c1x+1=ma(x)mb(x)(4)
上式中ma(x)和mb(x)分別為生成該gold序列的兩個m序列優選對的生成多項式。圖1為基于m序列優選對產生gold序列的原理圖。
考慮根據序列的線性遞推關系可以表示為齊次線性方程:
理論上我們只要找到符合上述齊次線性方程組的(1,c1,c2,…,cl-1,cl)的解,即為序列的生成多項式。
由于序列在傳輸過程中不可避免將受到信道中噪聲的影響,在接收序列中不可避免的會出現誤碼,不能保證在正確生成多項式的情況下式(7)中的方程組全部都能成立,因此對l階序列建立方程組如下:
在無誤碼情況下,若
且s越大,估計多項式是生成多項式的可能越大。設置閾值t,若s≥t就認為此時的估計多項式是真實生成多項式。
由于m序列的初始狀態決定由本原多項式生成的序列的相位,又gold序列又兩個m序列優選對生成的序列移位模二加,因此m序列的初始狀態可以決定最后生成的gold序列的初始狀態即相位。由于m序列的相位被其前n位初始狀態唯一確定,則可知gold序列的相位也被兩個m序列優選對的初始狀態唯一確定。由于m序列有位移性:m序列移位后還是該m序列,只是相位不同。
在上述估計方法得到gold序列的生成多項式和兩個優選對之后,初始化兩個m序列初始狀態,然后移位模二加并與截獲序列進行對比,對應位置相同的概率為80%時,認為此時的兩個m序列的前n位就是各自的初始狀態。
對m序列c進行循環移位得到tic(i=0,1…2n-2),因此考慮初始化兩個m序列ma(x)和mb(x)的初始狀態為[0,0,···,1],,對ma(x)生成的序列循環移位i=0次,對mb(x)生成的序列循環移位j=0次。有這兩個序列進行模2加后與原序列進行對比,若對應位置相同的概率大于80%,此時循環得到的兩個m序列的前n位分別為它們的初始狀態,否則若j<2n-2,則j=j+1,繼續執行步驟2。若j=2n-2,則i=i+1,繼續上述操作。
例1:取n=4階本原多項式ma(x)=1+x+x4產生的序列{a},初始狀態為[1001];取n=4階本原多項式mb(x)=1+x3+x4產生的序列{b},初始狀態為[1101]。
可知,ma(x)和mb(x)是一組m序列優選對,將mb(x)循環移位88次,構造的gold序列
其中
{a}=[100100011110101]
{b}=[110101111000100]
即各自初始狀態分別為[1001]、[1101]。{b}循環移位88次后初始狀態變為[0101]。構造的gold序列為
g=[110011111100110]
設置初始狀態為[0001],分別得到
{a}1=[000111101011001]
{b}1=[000100110101111]
經過算法識別后得對{a}1進行循環移位i=4次,mb(x)循環移位j=7次后得到的序列與原序列g完全相同。此時t4{a}1=[100100011110101]={a},t7{b}1=[010111100010011]=t88{b}。可知構成識別序列的兩個m序列的初始狀態分別為[1001]和[0101],識別正確,說明該方法有一定可行性。
本發明在此基礎上對gold序列的參數進行了識別,包括生成多項式、兩個m優選對的本原多項式和各自的初始狀態。
具體步驟:
步驟1:截取長度為l的部分含誤碼n階gold序列。
步驟2:按照gold序列的階數n構造關于生成多項式的方程組,在gold序列生成多項式庫中進行搜索匹配,若出現方程組右邊為零的方程個數大于閾值的多項式就是gold序列的生成多項式,構造該生成多項式的兩個本原多項式就是兩個m序列優選對的本原多項式ma(x)和mb(x)。
步驟3:先固定ma(x)和mb(x)的初始狀態為[0001]。對ma(x)生成的序列循環移位i=0次,對mb(x)生成的序列循環移位j=0次。
步驟4:有這兩個序列進行模2加后與原序列進行對比,若對應位置相同的概率大于80%,算法結束,否則若j<2n-2,則j=j+1,繼續執行步驟2。若j=2n-2,則i=i+1,繼續執行步驟2.
ma(x)初始狀態為循環移位i次后的前n項,mb(x)初始狀態為循環移位i次后的前n項。
利用本發明提出的方法對gold序列的參數進行估計。圖2為含誤碼gold序列參數估計流程圖,本發明利用生成多項式庫搜索算法估計含誤碼的gold序列參數。
圖3為階數為13的gold序列在誤碼率為0.03條件下的生成多項式識別結果。將序列構造規模為1000的方程組后,設置閾值t2=200,在階數為13的m序列本原多項式中進行搜索匹配,從圖中可以看出,只有在多項式下標為133時的本原多項式對應的s大于閾值t2,該本原多項式為g(x)=x13+x12+x11+x9+x8+x6+x4+x3+1。該本原多項式就是序列的生成多項式,識別正確。
圖4為對10階和13階gold序列在不同誤碼率下的識別結果圖。對截獲序列劃分后構造規模為900的方程組,對生成多項式進行識別,做200次蒙特卡洛仿真。從圖上可以看出,截獲序列的階數越低,本發明的方法識別效果越好。
- 還沒有人留言評論。精彩留言會獲得點贊!