一種高維混沌系統下的彩色二維碼加解密方法與流程

本發明屬于計算機圖像處理與信息安全技術應用領域，特別是涉及一種高維混沌系統下的彩色二維碼加解密方法。

背景技術：

彩色二維碼作為數字媒體在網絡應用中是較為常用的一種形式，兼具美觀實用、存儲信息量大和容錯能力強的優點，但缺點是易被偽造、易攜帶病毒釣魚信息、抗攻擊能力弱。由于目前的經典加密方法已不適應彩色二維碼的加解密需求，所以彩色二維碼加解密方法研究成為學術界的研究熱點。

adleman提出dna分子編碼與計算方法至今，dna編碼與計算方法已廣泛應用于圖像加密、身份驗證、數字簽名等相關領域中。其中基于dna計算的新型加密方法，在密鑰傳遞和分發方面面臨較大困難。為了提高圖像加密效率，某些學者提出基于混沌系統的圖像加密方法，通過將dna技術和混沌系統結合，首先，提出了基于低維混沌系統和多混沌系統的圖像加密算法，其次，提出基于dna序列加法運算和混沌序列的圖像加密算法，最后，提出基于dna序列并結合混沌映射的rgb圖像加密算法。由于上述方法均基于低維混沌映射，導致加密圖像的抗攻擊能力較弱。為了解決上述問題，有學者提出了采用sha-256生成一維混沌系統初始值并利用布朗運動多次迭代置亂實現圖像加密的方法，但該方法的時間復雜度隨像素值的置亂和擴散迭代次數大幅提升。然后又提出了基于lorenz系統的圖像隱寫加密方法，但該方法在加密圖像的恢復質量方面不夠理想。將彩色二維碼分層處理，通過增加每種顏色的通道和數據容量來提高彩色二維碼的安全性，這種方法由于處理方式單一會導致加密效率不夠理想。

技術實現要素：

為了解決上述問題，本發明的目的在于提供一種融合lorenz混沌系統、dna序列和sha-256散列算法的高維混沌系統下的彩色二維碼加解密方法。

為了達到上述目的，本發明提供的高維混沌下彩色二維碼加解密方法包括按順序進行的下列步驟：

步驟1：使用sha-256散列算法處理彩色二維碼，生成加密密鑰k和lorenz混沌系統的初始值；

步驟2：設定多種dna序列編解碼規則；

步驟3：將上述彩色二維碼分解成r,g,b三個矩陣，然后將每個矩陣分別變換為二進制彩碼矩陣r(m,n×8)，g(m,n×8)，b(m,n×8)，之后從上述多種dna序列編解碼規則中選擇一種規則并分別編碼上述三個二進制彩碼矩陣，得到三個dna序列彩碼矩陣pr(m,n×4)，pg(m,n×4)，pb(m,n×4)；

步驟4：將上述加密密鑰k轉換為二進制加密密鑰序列kb，然后重復t次二進制加密密鑰序列kb(t＝(m×n×8)/32)而生成二進制加密密鑰矩陣mk(m,n×8)；之后使用與上述步驟3中相同的編碼規則編碼二進制加密密鑰矩陣mk，得到dna序列加密密鑰矩陣mke；

步驟5：根據dna異或運算規則將上述三個dna序列彩碼矩陣pr，pg，pb和dna序列加密密鑰矩陣mke分別進行異或運算而得到三個第一二進制中間矩陣pr’，pg’，pb’；

步驟6：利用lorenz系統和k1-k11、k12-k22、k23-k32三部分的加密密鑰x，y，z生成的lorenz系統初始值x0，y0，z0形成三個長度分別是(m×n×4)的混沌實數序列xn，yn，zn；

步驟7：根據上述混沌實數序列xn，yn，zn采用混沌序列的索引函數計算得到索引值lx，ly，lz；

步驟8：將上述步驟5)得到的第一二進制中間矩陣pr’，pg’，pb’分別轉化為向量vr(m×n×4)，vg(m×n×4)，vb(m×n×4)，然后結合步驟7中得到的索引值lx，ly，lz將向量vr，vg，vb置亂而得到三個第二二進制中間矩陣vr’，vg’，vb’；

步驟9：將上述三個第二二進制中間矩陣vr’,vg’,vb’分別轉化為三個第三二進制中間矩陣re(m×n×4)，ge(m×n×4)，be(m×n×4)，然后從上述多種dna序列編解碼規則中選擇一種規則解碼第三二進制中間矩陣re，ge，be，得到三個第四二進制中間矩陣rb，gb，bb；

步驟10：將上述三個第四二進制中間矩陣rb，gb，bb合并還原得到加密的彩色二維碼；

步驟11：解密時按照上述步驟10至步驟1進行逆操作，最后得到還原后的彩色二維碼。

在步驟1中，所述的使用sha-256散列算法處理彩色二維碼，生成加密密鑰k和lorenz混沌系統的初始值的方法是：

使用sha-256散列算法處理彩色二維碼而生成彩色二維碼的256位散列值，將該散列值定義為加密密鑰k；

將加密密鑰k分成32塊，ki表示第i塊，每塊8位，加密密鑰k由式(1)表示為：

k＝k1,k2,k3,...,k32(1)

分別將上述已分成32塊的加密密鑰k按順序分成三部分，分別是k1-k11、k12-k22、k23-k32，相應的加密密鑰為x,y,z，然后利用這三部分的加密密鑰x，y，z計算lorenz混沌系統的初始值(x0，y0，z0)：

在步驟2中，所述的多種dna序列編解碼規則如下面表1所示；

表1dna序列編解碼規則

在步驟5中，所述的進行異或運算所采用的公式為：

在步驟7中，所述的混沌序列的索引函數如式(5)所示：

(@,@)＝sort(@)表示混沌序列的索引函數，fx，fy，fz分別是x，y，z的新序列，lx，ly，lz分別表示fx，fy，fz的索引值。

在步驟8中，所述的置亂時所采用的公式為：

本發明提供的高維混沌系統下的彩色二維碼加解密方法，定義了高維混沌系統下dna序列和sha-256算法的使用方法并將其應用到了彩色二維碼的加解密中。加密方法涉及密鑰和初始值生成；利用dna編碼；彩碼密鑰矩陣異或操作；彩碼矩陣數值置換；利用dna解碼；合成加密彩色二維碼等步驟。解密方法是對加密方法的逆操作。從模擬實驗中可以看出，本發明方法具有較好的偽隨機性、防偽造性和抗攻擊性。

附圖說明

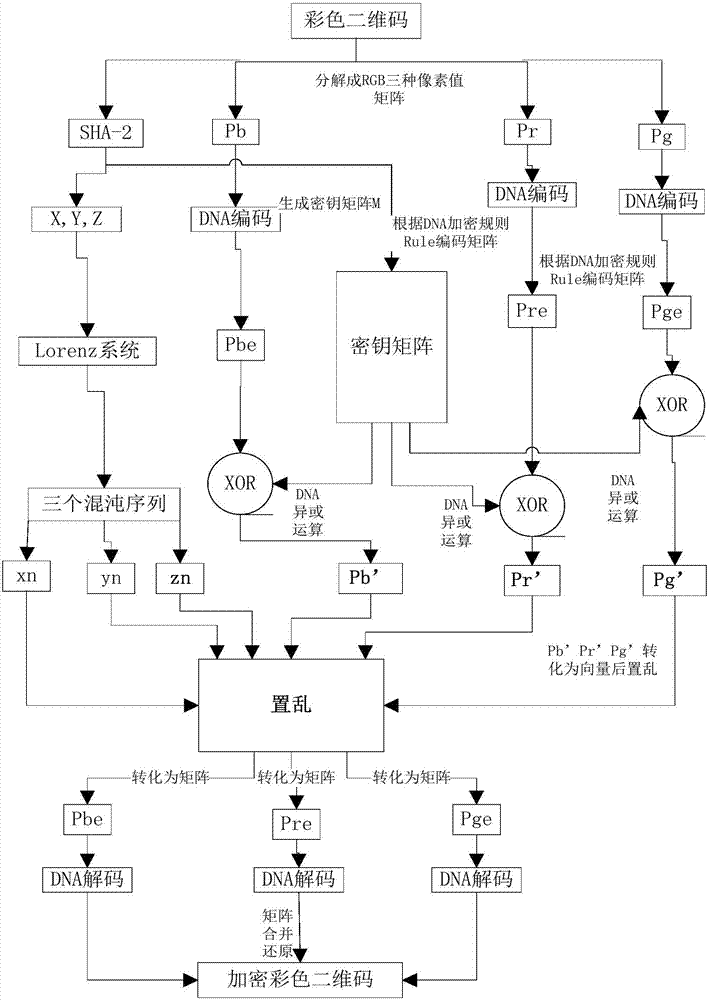
圖1為本發明提供的高維混沌系統下的彩色二維碼加解密方法中加密過程流程圖；

圖2為本發明提供的高維混沌系統下的彩色二維碼加解密方法中解密過程流程圖；

圖3為彩色二維碼加解密效果圖；

圖4為不同密鑰加密的彩色二維碼圖；

圖5為兩組加密前后彩色二維碼圖像像素三色直方圖；

具體實施方式

下面結合附圖和具體實例對本發明提供的高維混沌系統下的彩色二維碼加解密方法進行詳細說明。

如圖1、圖2所示，本發明提供的高維混沌系統下的彩色二維碼加解密方法包括按順序進行的下列步驟：

步驟1：使用sha-256散列算法處理彩色二維碼，生成加密密鑰k和lorenz混沌系統的初始值；

使用sha-256散列算法處理彩色二維碼而生成彩色二維碼的256位散列值，將該散列值定義為加密密鑰k，用于對彩色二維碼加密，以提高彩色二維碼的安全性。

將加密密鑰k分成32塊，ki表示第i塊，每塊8位，加密密鑰k由式(1)表示為：

k＝k1,k2,k3,...,k32(1)

lorenz混沌系統屬于三維混沌系統，具有初值敏感的特性，因此分別將上述已分成32塊的加密密鑰k按順序分成三部分，分別是k1-k11、k12-k22、k23-k32，相應的加密密鑰為x,y,z，然后利用這三部分的加密密鑰x，y，z計算lorenz混沌系統的初始值(x0，y0，z0)：

步驟2：設定多種dna序列編解碼規則，本發明使用表1所示的8種dna序列編解碼規則；

表1dna序列編解碼規則

步驟3：將上述彩色二維碼分解成r,g,b三個矩陣，然后將每個矩陣分別變換為二進制彩碼矩陣r(m,n×8)，g(m,n×8)，b(m,n×8)，之后從上述多種dna序列編解碼規則中選擇一種規則并分別編碼上述三個二進制彩碼矩陣，得到三個dna序列彩碼矩陣pr(m,n×4)，pg(m,n×4)，pb(m,n×4)；

步驟4：將上述加密密鑰k轉換為二進制加密密鑰序列kb，然后重復t次二進制加密密鑰序列kb(t＝(m×n×8)/32)而生成二進制加密密鑰矩陣mk(m,n×8)；之后使用與上述步驟3中相同的編碼規則編碼二進制加密密鑰矩陣mk，得到dna序列加密密鑰矩陣mke；

步驟5：根據dna異或運算規則將上述三個dna序列彩碼矩陣pr，pg，pb和dna序列加密密鑰矩陣mke按公式(3)分別進行異或運算而得到三個第一二進制中間矩陣pr’，pg’，pb’；

步驟6：利用lorenz系統和k1-k11、k12-k22、k23-k32三部分的加密密鑰x，y，z生成的lorenz系統初始值x0，y0，z0形成三個長度分別是(m×n×4)的混沌實數序列xn，yn，zn；

步驟7：根據上述混沌實數序列xn，yn，zn采用公式(4)所示的混沌序列的索引函數計算得到索引值lx，ly，lz：

(@,@)＝sort(@)表示混沌序列的索引函數，fx，fy，fz分別是x，y，z的新序列，lx，ly，lz分別表示fx，fy，fz的索引值；

步驟8：將上述步驟5)得到的第一二進制中間矩陣pr’，pg’，pb’分別轉化為向量vr(m×n×4)，vg(m×n×4)，vb(m×n×4)，然后結合步驟7中得到的索引值lx，ly，lz將向量vr，vg，vb按公式(5)置亂而得到三個第二二進制中間矩陣vr’，vg’，vb’：

步驟9：將上述三個第二二進制中間矩陣vr’,vg’,vb’分別轉化為三個第三二進制中間矩陣re(m×n×4)，ge(m×n×4)，be(m×n×4)，然后從上述多種dna序列編解碼規則中選擇一種規則解碼第三二進制中間矩陣re，ge，be，得到三個第四二進制中間矩陣rb，gb，bb；

步驟10：將上述三個第四二進制中間矩陣rb，gb，bb合并還原得到加密的彩色二維碼；

步驟11：解密時按照上述步驟10至步驟1進行逆操作，最后得到還原后的彩色二維碼。

本發明人從lorenz系統初始數值精度和加密密鑰空間兩個方面對本發明提供的高維混沌系統下的彩色二維碼加解密方法的安全性進行了分析。

lorenz系統的初始值為x0，y0，z0三個數值，若精度為10¹⁴，密鑰空間大小將達到10⁴²。最理想的情況下sha-256散列算法抵抗攻擊的能力為ssha-256＝2¹²⁸，可得到總的密鑰空間為s＝2¹²⁸×10⁴²≈3.4×10⁸⁰，由此可見密鑰空間足夠大，足以抵抗窮舉攻擊。因此，本發明方法的密鑰空間較大，安全性較高。

圖3至圖5分別為本發明方法的仿真模擬，該仿真環境下的重點是對本發明方法加解密效果、密鑰靈敏度、抗攻擊能力進行實驗說明。

圖3為彩色二維碼加解密圖；從圖3的實驗結果可以看出，本發明方法具有較好的加解密效果，能夠滿足對彩色二維碼應用的保密性需求。

圖4為不同密鑰加密的彩色二維碼圖；從圖4的實驗結果可以看出，正確密鑰能夠實現對彩色二維碼精準解密，而存在微小偏差的錯誤密鑰解密的彩色二維碼與原彩色二維碼相差較大，表明本發明方法對密鑰具有較高的靈敏度，從而具備較高的防偽性。

圖5為兩組加密前后彩色二維碼圖像像素三色直方圖；圖5(a)為第一組，圖5(b)為第二組，每組中八張圖分別代表彩色二維碼、彩色二維碼紅色像素直方圖、彩色二維碼綠色像素直方圖、彩色二維碼藍色像素直方圖和加密彩色二維碼、加密彩色二維碼紅色像素直方圖、加密彩色二維碼綠色像素直方圖，加密彩色二維碼藍色像素直方圖。從圖5的仿真實驗結果可以看出，加密后的兩組彩色二維碼的圖像像素三色直方圖分布都比較均勻，說明加密彩色二維碼較好地隱藏了統計信息，具有一定的抗差分攻擊的能力。