一種基于自適應補償技術的分數階網絡系統狀態估計方法與流程
本發明涉及一種基于自適應補償技術的分數階網絡系統狀態估計方法,屬于網絡系統分析與控制技術領域。
背景技術:
網絡系統的分析與控制對于保證網絡系統安全穩定運行具有重要的意義。近年來,隨著量測技術的發展與進步,使得對網絡系統進行實時在線監測與控制成為了可能。在現有的研究中,借助于相量量測單元所獲取的實時量測信息,通過設計動態的狀態估計器,是實現網絡系統實時分析與控制的主要途徑。
一般情況下,首先通過相量量測單元進行量測,獲取現場量測數據,然后通過信息傳輸通道傳到控制中心,但是需要注意的是,在量測信息的傳輸過程中,量測數據會不可避免的發生數據隨機丟失的情況,所以,在進行網絡系統的動態估計器設計時必須計及量測信號發生丟包的情況。
分數階網絡系統由于可以更加精確的描述系統的結構,近年來被廣泛應用于各個領域,如運用在電力系統網絡中,可以更加精確的對電力系統中的節點電壓和電流進行預測和估計。目前,在現有的研究中,針對于線性分數階網絡系統量測數據發生隨機丟包的問題,相關研究人員提出了一些量測數據補償技術,但是這些方法的有效性是建立在量測噪聲和系統噪聲協方差矩陣已知的條件上的,而在工程的實際應用中,這些條件是往往是未知的。基于此,本發明設計了一種基于自適應補償技術的分數階網絡系統狀態估計方法,該方法不僅可以實現對丟包量測數據動態補償,而且可以動態獲取系統噪聲和量測噪聲所滿足的協方差矩陣,因此本發明方法具有更好的工程實用性。最后,實際的分數階網絡系統算例測試驗證了本發明方法的有效性和實用性。
技術實現要素:
發明目的:針對現有技術中存在的問題,本發明提供一種基于自適應補償技術的分數階網絡系統狀態估計方法。
技術方案:一種基于自適應補償技術的分數階網絡系統狀態估計方法,包括如下部分:
1)計及量測數據隨機丟包的線性分數階網絡系統模型
在假設各個相量量測單元各自獨立工作的前提下,運用二進制伯努利分布變量方法,對計及量測信號數據隨機丟包情況下的離散線性分數階網絡系統進行建模,模型的系統方程xk+1和輸出方程
δγxk+1=adxk+buk+wk
式中:δγ為分數階算子,γ=[n1,n2…np]t為分數階階次,xk+1表示k+1時刻的狀態矢量(維度為p),ad為系統矩陣,b為控制矩陣,uk為輸入變量,
式中n≥0是分數階階次,j≥0代表不同時刻。
2)量測數據丟包的自適應補償技術
一般情況下,對于m維的輸出變量,其量測噪聲所滿足的協方差矩陣可以描述為:
式中
由分析可知,當
基于此,本發明提出了量測數據丟包情形下系統噪聲和量測噪聲協方差矩陣qk,rk的動態估計方法,進而實現了對丟包量測數據的動態補償,其具體實施步驟如下:
(1)計算新息序列,計算公式如下
式中
(2)當取移動窗口大小為l時,計算窗口內新息序列sk的平均值,即新息矩陣cvk,其計算公式如下
(3)在上一步的基礎上,求取噪聲協方差矩陣qk,rk的動態估計值,計算公式如下
qk=gkcvkgkt
式中gk是k時刻的濾波增益,
3)在上述的基礎上,則可以通過下面的廣義分數階卡爾曼濾波方法對計及量測信號丟包的線性分數階網絡狀態進行估計,具體步驟如下,該方法在計算機中是依次按照如下步驟實現的:
(1)設定濾波相關的初始值,如狀態估計初始值
(2)計算k+1時刻的狀態預測值
式中
(3)利用自適應補償技術方法,計算k+1時刻的噪聲協方差矩陣值qk+1,rk+1;(具體步驟見量測數據丟包的自適應補償技術部分)
(4)計算k+1時刻的狀態預測誤差協方差
式中(·)t為求矩陣的轉置。
(5)計算k+1時刻的廣義卡爾曼濾波增益gk+1,計算公式如下
(6)計算k+1時刻的估計誤差協方差
式中i為對應維度的單位矩陣。
(7)計算k+1時刻的狀態估計值
(8)當k+1>n時則迭代停止,輸出估計結果;反之,則重復本部分步驟(2)-(7),進行下一時刻的狀態估計。
附圖說明
圖1為本發明實施例的方法流程圖;
圖2為實施例采用傳統分數階卡爾曼濾波方法的狀態估計結果圖,(a)為分數階卡爾曼濾波算法狀態估計結果,(b)為分數階卡爾曼濾波算法狀態估計結果;
圖3為實施例采用傳統分數階卡爾曼濾波方法的估計誤差圖,(a)為分數階卡爾曼濾波算法狀態估計誤差,(b)為分數階卡爾曼濾波算法狀態估計誤差;
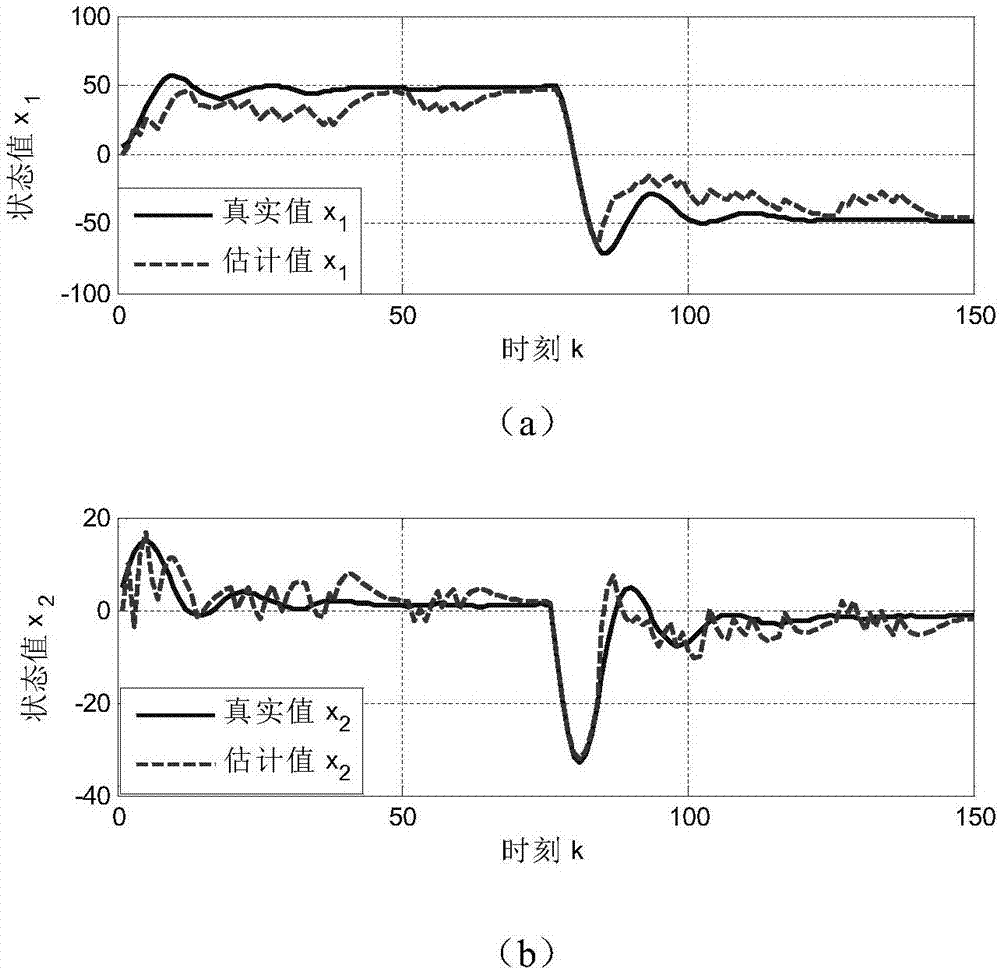
圖4為實施例采用本發明方法的狀態估計結果圖,(a)為本發明方法狀態估計結果,(b)為本發明方法狀態估計結果;
圖5為實施例采用本發明方法的狀態估計誤差圖,(a)為本發明方法狀態估計誤差,(b)為本發明方法狀態估計誤差。
具體實施方式
下面結合具體實施例,進一步闡明本發明,應理解這些實施例僅用于說明本發明而不用于限制本發明的范圍,在閱讀了本發明之后,本領域技術人員對本發明的各種等價形式的修改均落于本申請所附權利要求所限定的范圍。
如圖1所示,基于自適應補償技術的分數階網絡系統狀態估計方法,包括如下部分:
1)計及量測數據隨機丟包的線性分數階網絡系統模型
在假設各個相量量測單元各自獨立工作的前提下,運用二進制伯努利分布變量方法,對計及量測信號數據隨機丟包情況下的離散線性分數階網絡系統進行建模,模型的系統方程xk+1和輸出方程
δγxk+1=adxk+buk+wk
式中:δγ為分數階算子,γ=[n1,n2…np]t為分數階階次,xk+1表示k+1時刻的狀態矢量(維度為p),ad為系統矩陣,b為控制矩陣,uk為輸入變量,
式中n≥0是分數階階次,j≥0代表不同時刻。
2)量測數據丟包的自適應補償技術
一般情況下,對于m維的輸出變量,其量測噪聲所滿足的協方差矩陣可以描述為:
式中
由分析可知,當
基于此,本發明提出了量測數據丟包情形下系統噪聲和量測噪聲協方差矩陣qk,rk的動態估計方法,進而實現了對丟包量測數據的動態補償,其具體實施步驟如下:
(2)計算新息序列,計算公式如下
式中
(2)當取移動窗口大小為l時,計算窗口內新息序列sk的平均值,即新息矩陣cvk,其計算公式如下
(3)在上一步的基礎上,求取噪聲協方差矩陣qk,rk的動態估計值,計算公式如下
qk=gkcvkgkt
式中gk是k時刻的濾波增益,
3)在上述的基礎上,則可以通過下面的廣義分數階卡爾曼濾波方法對計及量測信號丟包的線性分數階網絡狀態進行估計,具體步驟如下
(1)設定濾波相關的初始值,如狀態估計初始值
(2)計算k+1時刻的狀態預測值
式中
(3)利用自適應補償技術方法,計算k+1時刻的噪聲協方差矩陣值qk+1,rk+1;
(4)計算k+1時刻的狀態預測誤差協方差
(5)計算k+1時刻的廣義卡爾曼濾波增益gk+1,計算公式如下
式中(·)-1為求矩陣的逆運算。
(6)計算k+1時刻的估計誤差協方差
式中i為對應維度的單位矩陣。
(7)計算k+1時刻的狀態估計值
(8)當k+1>n時則迭代停止,輸出估計結果;反之,則重復本部分步驟(2)-(7),進行下一時刻的狀態估計。
為了驗證本發明方法的有效性和實用性,下面介紹在分數階網絡系統研究中廣泛應用的一個分數階網絡系統,具體如下
yk=[0.10.3]xk+vk
式中分數階階次n1=0.7,n2=1.2,相量量測單元量測數據的隨機丟包率為0.3,系統噪聲wk和量測噪聲vk所滿足的協方差矩陣分別為
在運用本發明方法對實施例非線性分數階網絡進行狀態估計時,狀態估計的初始值x0=[00]t;最大迭代估計時刻n=150,自適應補償技術移動窗口值l=10,初始狀態估計誤差協方差矩陣
對上述實施例量測信號數據發生丟包的線性分數階網絡系統,分別運用傳統的分數階卡爾曼濾波算法(其所需的相關參數值和本發明方法的參數初值相同),以及本發明基于自適應補償技術的分數階網絡系統狀態估計方法對系統狀態變量進行估計。采用傳統的分數階卡爾曼濾波算法狀態估計結果如圖2所示,估計誤差如圖3所示;采用本法明方法的狀態估計結果如圖4所示,估計誤差如圖5所示。
綜合圖2和圖3所示的測試結果,可以得出如下結論:由于量測數據在傳輸通道中會發生數據隨機丟包,所以,傳統的分數階卡爾曼濾波狀態估計方法無法實現此種情況下的系統狀態精確估計。
綜合圖4和圖5所示的測試結果,可以得出如下結論:本發明基于自適應補償技術的分數階網絡系統狀態估計方法可以實現對量測數據的丟包動態補償,進而完成對系統狀態的準確追蹤和估計。
- 還沒有人留言評論。精彩留言會獲得點贊!