一種基于粒子群的自適應波束成型干擾抑制方法與流程
本發明涉及無線通信信號實時處理領域,特別涉及一種自適應波束成型干擾抑制方法,具體是一種基于粒子群的自適應波束成型干擾抑制方法。
背景技術:
基于頻域的經典濾波方法無法處理干擾信號頻率和期望信號頻率相接近的情況,這對于無線通信干擾抑制來說無疑是嚴重的缺陷。而自適應波束成型技術作為一種空域濾波器,能在提高期望信號增益的同時抑制干擾信號和噪聲信號,提高信干噪比,所以在很多無線通信信號實時處理領域獲得越來越廣泛的應用。
最小均方算法(Least Mean Square,LMS)是波束成型技術中的經典算法。LMS算法雖然簡單,但收斂速度緩慢,且容易陷入局部最優值。這對于高性能實時處理系統來說是嚴重的缺陷。
粒子群算法(Particles Swarm Optimization,PSO)屬于進化算法,由Kennedy和Eberhart于1995年提出,是一種群體智能搜索算法,其原理在于模擬鳥群覓食的過程搜索全局最優解。與諸如遺傳算法、退火算法等進化算法相比,粒子群除了具有易于硬件實現的優勢外,在搜索全局最優值和收斂速度方面的性能也更加優越。然而,傳統的粒子群方法無法完全避免陷入局部最優值,且容易出現早熟的情況,尤其是解決多峰值尋優問題時更是如此。
技術實現要素:
本發明要解決的技術問題是:針對現有波束成型算法收斂速度慢,容易陷于局部最優等不足,通過對粒子群算法進行改進,提供一種基于分區間粒子群(Partition Particles Swarm Optimization,PPSO)的自適應波束成型干擾抑制方法。
本發明技術方案的基本思路是:本發明在經典粒子群方法的基礎上,將解空間分成多個子相位空間,然后在每一個子相位空間運用粒子群方法來搜索相應相位空間中的最優值。最后從所有子相位空間最優值中挑選出整個相位空間的最優值。
本發明的技術方案是:一種基于粒子群的自適應波束成型干擾抑制方法,其特征在于,包括以下步驟:
第一步,構建一個具有N個陣元的均勻分布線陣列的自適應波束成型模型;
為表述方便,設時刻n天線陣接收原始輸入信號XN(n)=[X0(n),…,XN-1(n)]T,N為天線陣元數量,S(n)是參考信號,E(n)是誤差信號,WN(n)=[W0(n),…,WN-1(n)]T為權向量,Y(n)為輸出信號,以上各參數均為復數;
第二步,將解空間分成多個子相位空間;
第(1)步,將解空間映射到相位空間,轉換成幅角公式,其表示如下:
其中,|wi|,分別表示Wi的幅值和相位,i=0,1,…N-1。簡化上述公式,表示如下:
其中,
這樣,[φ1,…,φN-1]為解向量;
記φi∈Ri,則R1×R2×…×RN-1構成了N-1維相位搜索空間;
此時,自適應波束成型的輸出信號則為如下形式:
W0*表示W0的共軛,表示的共軛轉置。
定義歸一化輸出如下:
定義歸一化期望信號如下:
第(2)步,將相位搜索空間分割成子相位搜索空間;
將Ri分成M等分{Ri1,…,RiM},1=1,…N-1,M是2的倍數,d=1,…M,則相位搜索空間被分割成MN-1個N-1維的子相位搜索空間:
ψd=R1l×…×RN-1,m,l,m=1,…M,d=1,…MN-1
第三步,采用分區間粒子群優化算法對每個子相位搜索空間求最優解:
第(1)步:初始化子相位搜索空間ψd的基本粒子:
為簡化起見,ψd記為
設置粒子個數為m;
第i個粒子在第k次迭代時的位置向量:
第i個粒子在第k次迭代時的速度向量:
第i個粒子歷史最優位置:Ppbest=(pbest1,pbest2,...pbestN-1);
粒子群全局歷史最優位置:Pgbest=(pgest1,pgest2,...pgestN-1);
隨機初始化基本粒子及初始速度,k=1;
第(2)步:更新粒子的速度和位置:
粒子的速度和位置更新公式設置如下:
其中,c1,c2是兩個常數,通常為2;r1,r2是兩個范圍為[0,1]的隨機數;ωk是慣性權重,主要用來平衡算法的局部和全局搜索能力;
其中,1>ωmax>ωmin>0,ωmax,ωmin分別為ω的最大值和最小值,k為迭代次數,K為迭代次數的上限;
根據以上公式更新粒子群,得到新的粒子群;
第(3)步,計算適應度函數:
優化的目標是最小化適應度函數;
第(4)步,在滿足收斂條件時,得到該子相位搜索空間ψd的最優解否則,返回第三步第(2)步繼續執行;
其中,所述的收斂條件為:
J≤ε(ε為一個極小值)或者迭代次數達到設置值;
第四步,對上面得到的各個子相位搜索空間最優值求全局最優值:
發明附圖
圖1是本發明算法總體流程圖;
圖2是自適應波束成型空域濾波模型圖;
圖3是4×4分區間粒子的初始相位分布圖;
圖4是本發明PPSO和標準LMS算法所對應的幅度方向圖;
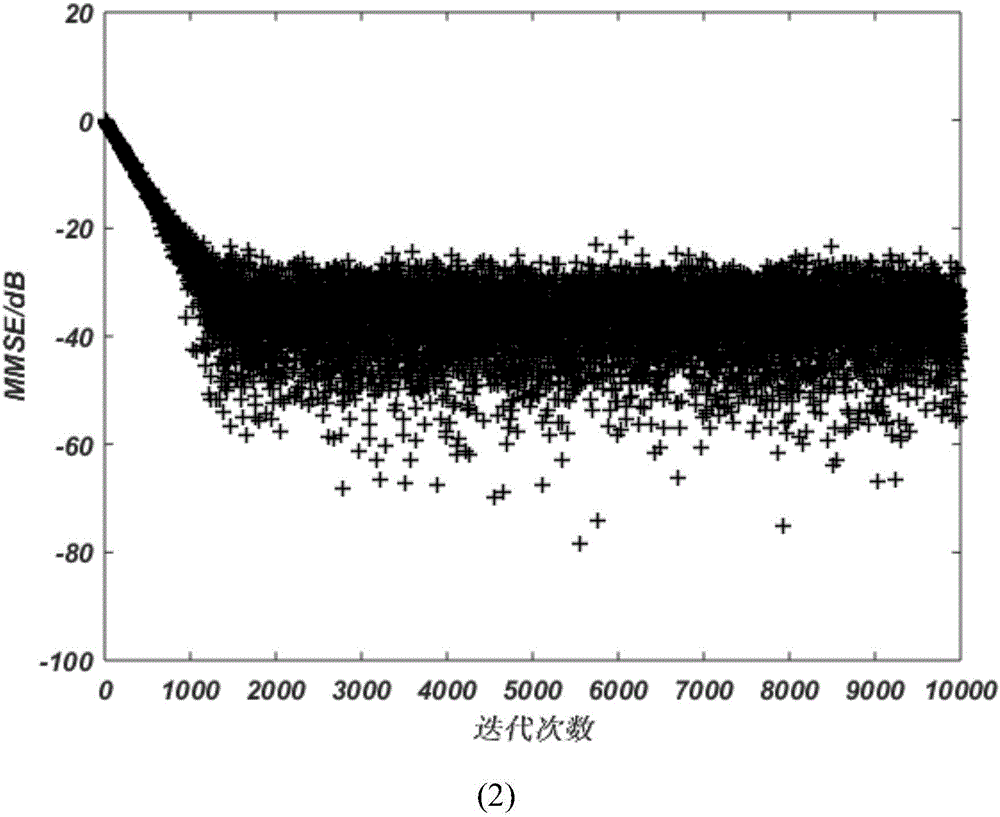
圖5是算法的均方誤差(Mean Squared Error,MSE)收斂曲線圖;
具體實施方式
下面以一個三天線自適應波束成型干擾抑制這一具體實例說明本發明的實施方式,圖1是本發明的總體流程圖,整個流程可分為四個大的步驟:
第一步,構建一個具有三個陣元的均勻分布線陣列的自適應波束成型模型;
圖2是自適應波束成型空域濾波模型圖,其中,ADC表示模數轉換器(Analog Digital Converter);
為表述方便,設時刻n的三天線陣接收原始輸入信號X3(n)=[X0(n),X1(n),X2(n)]T,S(n)是參考信號,E(n)是誤差信號,W3(n)=[W0(n),W1(n),W2(n)]T為權向量,Y(n)為輸出信號,以上各參數均為復數;
第二步,將解空間分成多個子相位空間;
第(1)步,將解空間映射到相位空間,轉換成幅角公式,其表示如下:
其中,|wi|,分別表示Wi的幅值和相位,i=0,1,2。簡化上述公式,表示如下:
其中,
這樣,[φ1,φ2]為解向量;
記φi∈Ri,i=1,2,則R1×R2構成了二維相位搜索空間;
此時,自適應波束成型的輸出信號則為如下形式:
定義歸一化輸出如下:
定義歸一化期望信號如下:
第(2)步,將二維相位搜索空間分割成子相位搜索空間;
將Ri分成M等分{Ri1,…,RiM},1=1,…N-1,圖3是一個M=4,即將相位搜索空間R1×R2分割成16個子相位搜索空間的示例說明;
圖3為一個4行4列共16個方塊組成的圖像,橫坐標代表R1的取值范圍,縱坐標代表R2的取值范圍,分別為[-π,-π),將Ri分成4等分,得到這樣相位搜索空間被分割成16個二維的子相位搜索空間:
ψd=R1l×R2m,l,m=1,…4,d=1,…16
也就是圖3的每個方塊,其橫坐標和縱坐標對應其子相位搜索空間的取值范圍;
第三步,采用分區間粒子群優化算法對每個子相位搜索空間求最優解:
第(1)步:初始化子相位搜索空間ψd的基本粒子:
為簡化起見,ψd記為
設置粒子個數為m,取為8,隨機初始化基本粒子的位置及初始速度;
圖3中每個小方塊代表一個子相位搜索空間,其中的小顆粒代表第i個粒子在第k次迭代時的位置向量;
第i個粒子在第k次迭代時的位置向量:
第i個粒子在第k次迭代時的速度向量:
第i個粒子歷史最優位置:Ppbest=(pbest1,pbest2,...pbestN-1);
粒子群全局歷史最優位置:Pgbest=(pgest1,pgest2,...pgestN-1);
第(2)步:更新粒子的速度和位置:
其中,c1,c2是兩個常數,取為2;r1,r2是兩個范圍為[0,1]的隨機數;ωk是慣性權重,主要用來平衡算法的局部和全局搜索能力;
其中,1>ωmax>ωmin>0,ωmax,ωmin分別為ω的最小值和最大值,分別取值為0.9和0.4,k為迭代次數,K為迭代次數的上限,取為1000;
根據以上公式更新粒子群,得到新的粒子群;
第(3)步,計算適應度函數:
優化的目標是最小化適應度函數;
第(4)步,在滿足條件J≤10-4或者迭代次數達到1000時,得到該子相位搜索空間ψd的最優解否則,返回第三步第(2)步繼續執行;
第四步,對上面得到的各個子相位搜索空間最優值求全局最優值:
圖4表示本發明PPSO和標準LMS算法所對應的幅度方向圖,橫坐標表示角度[-180°,180°],縱坐標表示歸一化幅度值,該圖表示信號入射方位角與自適應濾波器空域增益關系。其中藍色、紅色、綠色和黑色曲線分別對應PSO、分割成4個區間的PPSO(2×2PPSO)、分割成16個區間的PPSO(4×4PPSO)和LMS算法所得到的幅度方向圖。由圖可知,所有的這些算法都能對60°方向(干擾方向)的信號進行零陷處理并在0°方向(期望信號方向)的信號提供很好的幅度增益,也就是對干擾方向的信號進行抑制的同時保護期望信號,其中分割成4×4區間的PPSO可以獲得最大的信號增益,而LMS則對應獲得最小的信號增益。
圖5分別展示了2×2PPSO和4×4PPSO算法和步長因子為0.001(為了獲得更小的均方誤差曲線的方差值)算法對應的MSE性能曲線。其橫坐標表示算法迭代次數,而縱坐標表示dB值。其中圖5(1)中紅色、綠色和藍色曲線分別對應4×4PPSO、2×2PPSO和標準PSO算法,圖5(2)中的曲線對應LMS算法。由圖可以看出2×2PPSO和4×4PPSO(4×4PPSO的MSE曲線更低)算法在迭代2000次左右時便可以穩定收斂,PSO算法則需要迭代4000次左右,LMS則需要15000次左右才能獲得穩定的收斂結果,由此可以判斷PPSO算法可以獲得更快更好的收斂性能,比標準PSO算法和LMS算法都更加快速地收斂。
- 還沒有人留言評論。精彩留言會獲得點贊!