一種信號量化情形下的混沌神經網絡保密通信方法與流程

本發明屬于網絡通信技術領域，涉及神經網絡保密通信方法，具體地說，涉及了一種信號量化情形下的混沌神經網絡保密通信方法。

背景技術：

自Pecora和Carroll于1990年發現混沌系統的同步方法以來，混沌在保密通信中的應用成為了信息安全領域的研究熱點。混沌信號由于具有類隨機、非周期以及不可預測等特點，可以作為密文信息的載體。混沌神經網絡通常具有結構簡單、動態性能復雜等特點，非常適合作為混沌信號的發生器，因此，混沌神經網絡保密通信技術具有廣闊的應用前景。

隨著計算機網絡技術的飛速發展，網絡成為通信領域信息傳遞的主要方式，現有的混沌保密通信方案大多也是基于網絡提出的。但由于網絡環境中的信號必須是數字信號，而混沌系統對初值又極端敏感，所以網絡環境中特有的量化誤差往往會對保密通信過程造成很大的影響。然而，現有的混沌保密通信方案幾乎不能處理信號量化問題。因此，實現設計在信道量化情形下的保密通信方案具有重要的研究意義。

技術實現要素：

本發明針對現有混沌保密通信過程中存在的不能處理信號量化問題的不足提供一種信號量化情形下的混沌神經網絡保密通信方法，該方法能夠有效地處理混沌保密通信過程中均勻量化和隨機擾動帶來的影響。

為了達到上述目的，本發明提供了一種信號量化情形下的混沌神經網絡保密通信方法，含有以下步驟：

(一)建立混沌神經網絡模型以及量化器模型。

建立如下混沌神經網絡模型:

x(k+1)＝Ax(k)+Bf(x(k))+W₁ω₁(k) (1)

其中，x(k)＝[x₁(k),x₂(k),x₃(k)]^T是k時刻混沌神經網絡的狀態向量，x₁(k)、x₂(k)、x₃(k)分別表示神經元1,2,3的狀態，T表示矩陣的轉置，f(x(k))＝[f₁(x₁(k)),f₂(x₂(k)),f₃(x₃(k))]^T是激勵函數向量，f_i(x_i(k))＝(|x_i(k)+1|-|x_i(k)-1|)/2,(i＝1,2,3)是第i個神經元的激勵函數，x_i(k)表示k時刻第i個神經元的狀態，ω₁(k)是混沌神經網絡模型內的有界隨機擾動向量，系數矩陣A,B,W₁分別是狀態向量x(k)、激勵函數向量f(x(k))、擾動向量ω₁(k)對應的連接矩陣；

令混沌神經網絡模型為驅動系統,建立響應系統模型如下:

y(k+1)＝Ay(k)+Bf(y(k))+W₂ω₂(k)+u(k) (2)

其中，y(k)＝[y₁(k),y₂(k),y₃(k)]^T是響應系統的狀態向量，f(y(k))＝[f₁(y₁(k)),f₂(y₂(k)),f₃(y₃(k))]^T表示響應系統的激勵函數向量，響應系統的激勵函數與驅動系統的相同，u(k)是控制器輸入，ω₂(k)是響應系統內的有界隨機擾動向量，系數矩陣A,B和驅動系統相同，W₂是擾動向量ω₂(k)的連接矩陣；

設定均勻量化的量化規則，建立量化器模型，量化器模型表示為：

式中，x_i(k)是k時刻x_i的測量值，x_i表示驅動系統第i個神經元的狀態，U是量化器的量化區間，Δ是量化精度，[·]表示四舍五入的取整函數；

定義量化向量為q(x(k))＝[q₁(x₁(k)),q₂(x₂(k)),q₃(x₃(k))]^T，

則量化誤差為ε_x(k)＝q(x(k))-x(k)；

同理，定義量化向量為q(y(k))＝[q₁(y₁(k)),q₂(y₂(k)),q₃(y₃(k))]^T，

則量化誤差為ε_y(k)＝q(y(k))-y(k)。

(二)構造狀態反饋控制器，獲得誤差動力學系統。

定義驅動系統和響應系統的同步誤差為e(k)＝y(k)-x(k)，構造狀態反饋控制器，并表示為：

其中，K是控制器增益矩陣，ε_e(k)＝ε_y(k)-ε_x(k)，則n＝3表示驅動系統和響應系統的維數；

因此，驅動系統和響應系統的誤差動力學系統為：

e(k+1)＝Ae(k)+Bh(e(k))+Ke(k)+Kε_e(k)-W₁ω₁(k)+W₂ω₂(k) (5)

其中，h(e(k))＝f(y(k))-f(x(k))是激勵函數的誤差向量。

(三)求解控制器增益矩陣K，代入實際的控制器中，獲得同步控制器。

構造如下線性矩陣LMI：

其中，P＞0為未知的正定矩陣，ψ＞0,λ＞0,ρ₁＞0,ρ₂＞0,ρ₃＞0均為未知的正實數，M為已知的常數矩陣，X＝PK為所要求解的矩陣，I為單位矩陣；

利用MATLAB中的LMI工具箱求解公式(6)，得到矩陣P和X，從而得出控制器增益矩陣K＝P^-1X，其中，上標“-1”代表矩陣P的逆；

將求解出的增益矩陣K，代入實際的控制器中，獲得同步控制器。

(四)驅動系統加載密文信號得到疊加信號，通過網絡傳送到響應系統。

驅動系統產生三維的混沌信號x₁(k),x₂(k),x₃(k)，其中，信號x₃(k)與原始的密文信號s(k)相疊加產生疊加信號l(k)＝x₃(k)+s(k)，經過量化器模型處理后的三維信號q(x₁(k)),q(x₂(k)),q(l(k))通過網絡傳送到響應系統，其中，q(l(k))為量化后的疊加信號；

(五)在同步控制器作用下，使驅動系統和響應系統的同步。

響應系統接收到三維信號q(x₁(k)),q(x₂(k)),q(l(k))，其中，q(x₁(k)),q(x₂(k))傳送到同步控制器中，在同步控制器的作用下，使驅動系統和響應系統同步；響應系統產生同步信號y₃(k)，經量化器模型處理后為同步信號q(y₃(k))。

(六)由疊加信號和同步信號得到恢復的密文信號。

由量化后的疊加信號q(l(k))和同步信號q(y₃(k))做差，得到恢復的密文信號從而完成信號量化情形下的混沌神經網絡保密通信。

與現有技術相比，本發明的有益效果在于：

本發明提供的保密通信息方法，考慮了網絡環境中的均勻量化現象，提出了一種同步控制器，在同步控制器的作用下，實現驅動系統和響應系統的同步，由量化后的疊加信號和同步信號得到恢復的密文信號，能夠有效消除均勻量化和隨機干擾帶來的影響，達到在信號量化情形下保密通信的目的。

附圖說明

圖1為本發明實施例信號量化情形下的混沌神經網絡保密通信方法的流程圖。

圖2為本發明實施例信號量化情形下的混沌神經網絡保密通信方法中驅動系統混沌吸引子x₁-x₂投影圖。

圖3為本發明實施例信號量化情形下的混沌神經網絡保密通信方法中驅動系統混沌吸引子x₁-x₃投影圖。

圖4為本發明實施例信號量化情形下的混沌神經網絡保密通信方法中驅動系統混沌吸引子x₂-x₃投影圖。

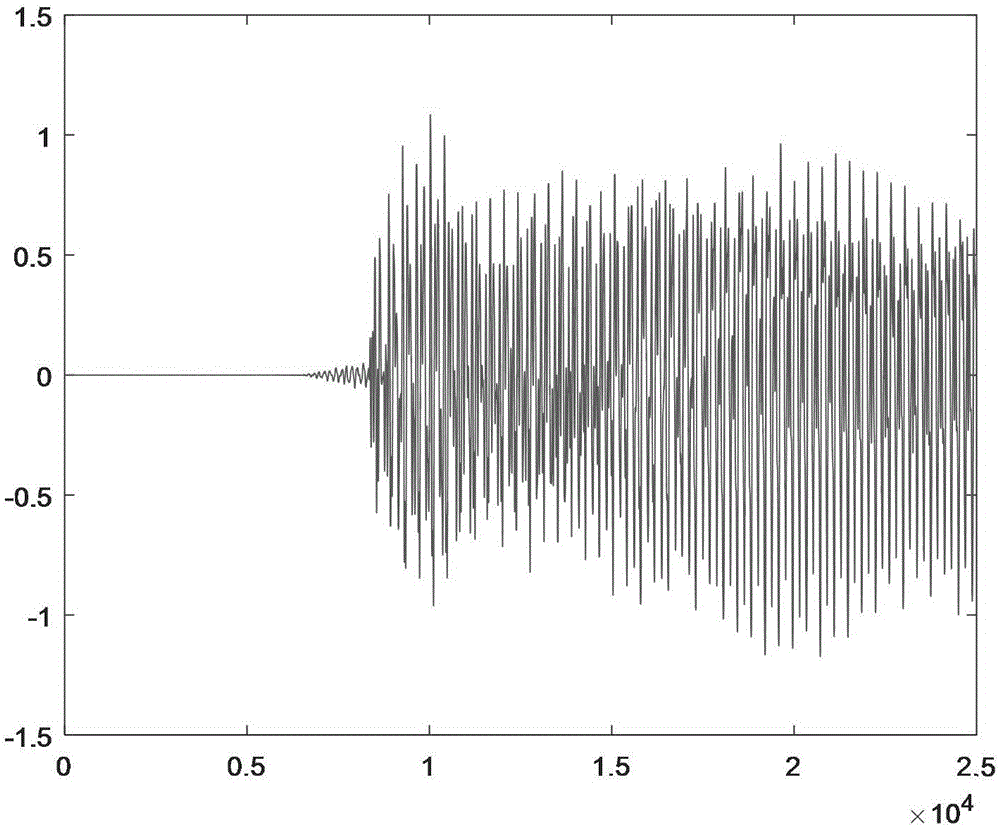
圖5為本發明實施例1發送端原始的密文信號時域圖。

圖6為本發明實施例1網絡傳輸通道中的加密信號時域圖。

圖7為本發明實施例1接收端恢復的密文信號時域圖。

圖8為本發明實施例1發送端原始的密文信號與接收端恢復的密文信號的誤差示意圖。

圖9為本發明實施例2發送端原始的密文信號時域圖。

圖10為本發明實施例2網絡傳輸通道中的加密信號時域圖。

圖11為本發明實施例2接收端恢復的密文信號時域圖。

圖12為本發明實施例2發送端原始的密文信號與接收端恢復的密文信號的誤差示意圖。

具體實施方式

下面，通過示例性的實施方式對本發明進行具體描述。然而應當理解，在沒有進一步敘述的情況下，一個實施方式中的元件、結構和特征也可以有益地結合到其他實施方式中。

參見圖1，本發明提供了一種信號量化情形下的混沌神經網絡保密通信方法，含有以下步驟：

步驟一:建立混沌神經網絡模型以及量化器模型。

建立如下混沌神經網絡模型:

x(k+1)＝Ax(k)+Bf(x(k))+W₁ω₁(k) (1)

其中，x(k)＝[x₁(k),x₂(k),x₃(k)]^T是k時刻混沌神經網絡的狀態向量，x₁(k)、x₂(k)、x₃(k)分別表示神經元1,2,3的狀態，T表示矩陣的轉置，f(x(k))＝[f₁(x₁(k)),f₂(x₂(k)),f₃(x₃(k))]^T是激勵函數向量，f_i(x_i(k))＝(|x_i(k)+1|-|x_i(k)-1|)/2,(i＝1,2,3)是第i個神經元的激勵函數，x_i(k)表示k時刻第i個神經元的狀態，ω₁(k)是混沌神經網絡模型內的有界隨機擾動向量，系數矩陣A,B,W₁分別是狀態向量x(k)、激勵函數向量f(x(k))、擾動向量ω₁(k)對應的連接矩陣；

令混沌神經網絡模型為驅動系統,建立響應系統模型如下:

y(k+1)＝Ay(k)+Bf(y(k))+W₂ω₂(k)+u(k) (2)

其中，y(k)＝[y₁(k),y₂(k),y₃(k)]^T是響應系統的狀態向量，f(y(k))＝[f₁(y₁(k)),f₂(y₂(k)),f₃(y₃(k))]^T表示響應系統的激勵函數向量，響應系統的激勵函數與驅動系統的相同，u(k)是控制器輸入，ω₂(k)是響應系統內的有界隨機擾動向量，系數矩陣A,B和驅動系統相同，W₂是擾動向量ω₂(k)的連接矩陣；

設定均勻量化的量化規則，建立量化器模型，量化器模型表示為：

式中，x_i(k)是k時刻x_i的測量值，x_i表示驅動系統第i個神經元的狀態，U是量化器的量化區間，Δ是量化精度，[·]表示四舍五入的取整函數；

定義量化向量為q(x(k))＝[q₁(x₁(k)),q₂(x₂(k)),q₃(x₃(k))]^T，

則量化誤差為ε_x(k)＝q(x(k))-x(k)；

同理，定義量化向量為q(y(k))＝[q₁(y₁(k)),q₂(y₂(k)),q₃(y₃(k))]^T，

則量化誤差為ε_y(k)＝q(y(k))-y(k)。

步驟二：構造狀態反饋控制器，獲得誤差動力學系統。

定義驅動系統和響應系統的同步誤差為e(k)＝y(k)-x(k)，構造狀態反饋控制器，并表示為：

其中，K是控制器增益矩陣，ε_e(k)＝ε_y(k)-ε_x(k)，則n＝3表示驅動系統和響應系統的維數；

因此，驅動系統和響應系統的誤差動力學系統為：

e(k+1)＝Ae(k)+Bh(e(k))+Ke(k)+Kε_e(k)-W₁ω₁(k)+W₂ω₂(k) (5)

其中，h(e(k))＝f(y(k))-f(x(k))是激勵函數的誤差向量。

步驟三：求解控制器增益矩陣K，代入實際的控制器中，獲得同步控制器。

構造如下線性矩陣LMI：

其中，P＞0為未知的正定矩陣，ψ＞0,λ＞0,ρ₁＞0,ρ₂＞0,ρ₃＞0均為未知的正實數，M為已知的常數矩陣，X＝PK為所要求解的矩陣，I為單位矩陣；

利用MATLAB中的LMI工具箱求解公式(6)，得到矩陣P和X，從而得出控制器增益矩陣K＝P^-1X，其中，上標“-1”代表矩陣P的逆；

將求解出的增益矩陣K，代入實際的控制器中，獲得同步控制器。

步驟四：驅動系統加載密文信號得到疊加信號，通過網絡傳送到響應系統。

驅動系統產生三維的混沌信號x₁(k),x₂(k),x₃(k)，混沌吸引子x₁-x₂投影圖參見圖2，混沌吸引子x₁-x₃投影圖參見圖3，混沌吸引子x₂-x₃投影圖參見圖4。其中，信號x₃(k)與原始的密文信號s(k)相疊加產生疊加信號l(k)＝x₃(k)+s(k)，經過量化器模型處理后的三維信號q(x₁(k)),q(x₂(k)),q(l(k))通過網絡傳送到響應系統，其中，q(l(k))為量化后的疊加信號。

步驟五：在同步控制器作用下，使驅動系統和響應系統的同步。

響應系統接收到三維信號q(x₁(k)),q(x₂(k)),q(l(k))，其中，q(x₁(k)),q(x₂(k))傳送到同步控制器中，在同步控制器的作用下，使驅動系統和響應系統同步；響應系統產生同步信號y₃(k)，經量化器模型處理后為同步信號q(y₃(k))；

步驟六：由疊加信號和同步信號得到恢復的密文信號。

由量化后的疊加信號q(l(k))和同步信號q(y₃(k))做差，得到恢復的密文信號從而完成信號量化情形下的混沌神經網絡保密通信。

實施例1：采用本發明上述方法對密文信號進行仿真，密文信號為window7系統關機時的聲音信號。

采用的參數為：

采樣周期T＝0.02s；

量化精度Δ＝0.02；

驅動系統初始值x₀＝[0.1,0.2,-0.1]^T；

響應系統初始值y₀＝[1,2,3]^T；

常數矩陣

通過公式(6)求解出控制器增益矩陣

發送端原始的密文信號時域圖參見圖5，網絡傳輸通道中的加密信號時域圖參見圖6，接收端恢復的密文信號時域圖參見圖7，原始的密文信號s(k)與恢復的密文信號做差得到保密通信誤差參見圖8所示。

由圖5至圖8可知，網絡傳輸的疊加信號與原始的密文信號差別很大，具有很強的保密性。此外，在信號均勻量化情形下，接收端可以把密文信號良好的恢復出來，原始的密文信號與恢復的密文信號之間的誤差很小。

實施例2：采用本發明上述方法對密文信號進行仿真，密文信號為劉歡的歌曲《我和你》的聲音信號。

采用的參數為：

采樣周期T＝0.02s；

量化精度Δ＝0.02；

驅動系統初始值x₀＝[0.1,0.2,-0.1]^T；

響應系統初始值y₀＝[2,1.5,2]^T；

常數矩陣

通過公式(6)求解出控制器增益矩陣

發送端原始的密文信號時域圖參見圖9，網絡傳輸通道中的加密信號時域圖參見圖10，接收端恢復的密文信號時域圖參見圖11，原始的密文信號s(k)與恢復的密文信號做差得到保密通信誤差參見圖12所示。

由圖9至圖12可知，網絡傳輸的疊加信號與原始的密文信號差別很大，具有很強的保密性。此外，在信號均勻量化情形下，接收端可以把密文信號良好的恢復出來，原始的密文信號與恢復的密文信號之間的誤差很小。

以上所舉實施例僅用為方便舉例說明本發明，并非對本發明保護范圍的限制，在本發明所述技術方案范疇，所屬技術領域的技術人員所作各種簡單變形與修飾，均應包含在以上申請專利范圍中。