超混沌隱藏吸引子產生電路及其構建方法與流程
本發明涉及一種含有隱藏吸引子的憶阻超混沌系統,在原有的Lü系統的第一方程添加磁控憶阻項、第二方程添加線性反饋項和外部激勵項。實現了一種磁控憶阻類Lü系統超混沌隱藏吸引子產生電路。
背景技術:
1971年提出了一種新的二端電路元件-憶阻器,并且從理論上預測了憶阻電荷與磁通量關系的存在性。2008年,美國惠普公司的研究人員將憶阻元件首次電路實現。2009年希捷公司的研究人員再次發明了一種基于電子磁性的自旋憶阻系統。近年來,憶阻元件因其具有非線性和記憶性,在人工神經網絡、保密通信、存儲器、生物模擬的研究預示存在廣闊的應用前景。憶阻的出現使得延續摩爾定律成為了可能,其記憶特性、納米級尺寸、快速開關以及耗電量低等特點為其各種應用的研究打下了堅實的基礎。并且,隨著材料、電子、系統、自動化等學科的發展,憶阻的研究和應用將會成為越來越熱門的研究方向。
基于憶阻的非線性,越來越多的學者開始將其應用到混沌電路的產生中,從而在保密通信中有著許多應用。雖然惠普公司和希捷公司相繼發明了憶阻元件的電路實現方法,但是其高昂的造價和較大的技術實現難度使得憶阻還無法達到商業化生產的水平。這使得許多研究人員還無法直接獲得相關的憶阻器件進行各種科學研究,因此,利用電阻、電容、電感、運算放大器、模擬乘法器等分立元器件實現了多種憶阻模擬器,或者基于特殊拓撲形式的電路構建了若干廣義憶阻模擬器,為憶阻及其應用電路的建模分析和實驗觀察做出了重要貢獻。本文提出了一種磁控憶阻類Lü系統超混沌隱藏吸引子產生電路,進一步地拓展了憶阻模擬器的實現形式。并且,本申請提出在四維條件下獲得的憶阻超混沌電路,沒有平衡點,且能夠產生超混沌隱藏吸引子,使得該系統具有更為復雜的動力學特性,預期該憶阻系統在保密通信密鑰產生等方面的具有潛在的應用價值。新系統所生成的新穎且奇異的隱藏吸引子,不同于傳統的自激吸引子,因為新系統不存在平衡點,其吸引盆與任何不穩定平衡點不相交,它是近年來新發現且新定義的一類吸引子,得到了學術界的廣泛關注并取得了大量研究成果。因此,研究新憶阻系統的實現方法及其存在的隱藏吸引子有著重要的物理意義。
技術實現要素:
本發明所要解決的技術問題是構建一種用于磁控憶阻類Lü系統的超混沌隱藏吸引子產生電路及其構建方法。
為了解決上述技術問題,本發明提供了一種超混沌隱藏吸引子產生電路,包括:振蕩系統和磁控憶阻對應的等效實現電路;其中所述振蕩系統適于通過與等效實現電路相連以呈現相應隱藏振蕩現象。
進一步,所述磁控憶阻等效實現電路包括:積分器,乘法器Ma、乘法器Mb,加法運算電路;其中所述磁控憶阻等效實現電路的輸入端對應的狀態變量–vy經過積分器的積分運算后輸出狀態變量vw,且該狀態變量vw經過乘法器Ma后與狀態變量–vy通過乘法器Mb完成乘法運算后,再通過加法運算電路輸出–gW(vw)vy。
進一步,所述加法運算電路包括:與等效實現電路的輸入端相連的第一電阻R/gα,與第二乘法器輸出端相連的第二電阻R/gβ,且第一、第二電阻的另一端相連后作為等效實現電路的輸出端;其中設置相應控制參數α=4和β=0.18。
進一步,所述振蕩系統包括:第一、第二和第三積分通道;其中
第一積分通道內包括第一積分器,其有兩個輸入端,即
一輸入端適于接入狀態變量vx,且串聯一電阻R/a后接到運算放大器U1的反相輸入端;
另一輸入端適于接入狀態變量–vy,且串聯另一電阻R/a后接于運算放大器U1的反相輸入端,該輸入端還串聯所述磁控憶阻器后接于運算放大器U1的反相輸入端,運算放大器U1的反相輸入端和輸出端之間并聯電容C1,且運算放大器U1的同相輸入端接地;
所述運算放大器U1的輸出端適于輸出狀態變量vx;以及
設置相應控制參數a=36;
第二積分通道內包括第二積分器和一級反相器,其分別對應四個輸入端,即
一輸入端適于接入狀態變量vx,且串聯一電阻R/d后接于運算放大器U2的反相輸入端;
另一輸入端適于接入狀態變量v1,且串聯一電阻R/2后接于運算放大器U2的反相輸入端;
第三輸入端適于接入狀態變量–vy,且串聯一電阻R/b后接于運算放大器U2的反相輸入端;
第四輸入端適于接入外部激勵項–μ,且串聯一電阻2R后接于運算放大器U2的反相輸入端,運算放大器U2的反相輸入端和輸出端之間并聯電容C2,所述運算放大器U2的輸出端適于輸出狀態變量vy;
運算放大器U2的輸出端和運算放大器U3的反相輸入端之間串聯一阻值為36kΩ的電阻,運算放大器U3的反相輸入端和輸出端之間并聯另一阻值36kΩ的電阻,運算放大器U2和運算放大器U3的同相輸入端均接地;
所述運算放大器U3的輸出端適于輸出狀態變量–vy;以及
設置相應控制參數b=20、d=5、μ=0.1和v1=vxvz;
第三積分通道內包括第三積分器,其分別對應兩個輸入端,即
一輸入端適于接入狀態變量v2,且串聯另一電阻R/2后接于運算放大器U4的反相輸入端;
另一輸入端適于接入狀態變量vz,且串聯一電阻R/c后接于運算放大器U4的反相輸入端,運算放大器U4的反相輸入端和輸出端之間并聯電容C3,運算放大器U4的同相輸入端接地;
所述運算放大器U4的輸出端適于輸出狀態變量vz;以及
設置控制參數c=3和v2=–vxvy;并且
所述輸入端v1和v2分別對應乘法器M1和乘法器M2的輸出端,其中
乘法器M1的兩輸入端分別對應輸入端vx和vz;以及
乘法器M2的兩輸入端分別對應輸入端vx和-vy。
又一方面,本發明還提供了一種超混沌隱藏吸引子產生電路的構建方法,包括如下步驟
步驟S1,建立磁控憶阻對應的等效實現電路;
步驟S2,建立振蕩系統;以及
步驟S3,將等效實現電路接入振蕩系統內以呈現相應隱藏振蕩現象。
進一步,所述磁控憶阻等效實現電路包括:積分器,乘法器Ma、乘法器Mb,加法運算電路;其中
所述磁控憶阻等效實現電路的輸入端對應的狀態變量–vy經過積分器的積分運算后輸出狀態變量vw,且該狀態變量vw經過乘法器Ma后與狀態變量–vy通過乘法器Mb完成乘法運算后,再通過加法運算電路輸出–gW(vw)vy。
進一步,所述加法運算電路包括:與等效實現電路的輸入端相連的第一電阻R/gα,與第二乘法器輸出端相連的第二電阻R/gβ,且第一、第二電阻的另一端相連后作為等效實現電路的輸出端;其中
設置相應控制參數α=4和β=0.18。
進一步,所述振蕩系統包括:第一、第二和第三積分通道;其中
第一積分通道內包括第一積分器,其有兩個輸入端,即
一輸入端適于接入狀態變量vx,且串聯一電阻R/a后接到運算放大器U1的反相輸入端;
另一輸入端適于接入狀態變量–vy,且串聯另一電阻R/a后接于運算放大器U1的反相輸入端,該輸入端還串聯所述磁控憶阻器后接于運算放大器U1的反相輸入端,運算放大器U1的反相輸入端和輸出端之間并聯電容C1,且運算放大器U1的同相輸入端接地;
此時所述運算放大器U1的輸出端適于輸出狀態變量vx;以及
設置相應控制參數a=36;
第二積分通道內包括第二積分器和一級反相器,其分別對應四個輸入端,即
一輸入端適于接入狀態變量vx,且串聯一電阻R/d后接于運算放大器U2的反相輸入端;
另一輸入端適于接入狀態變量v1,且串聯一電阻R/2后接于運算放大器U2的反相輸入端;
第三輸入端適于接入狀態變量–vy,且串聯一電阻R/b后接于運算放大器U2的反相輸入端;
第四輸入端適于接入外部激勵項–μ,且串聯一電阻2R后接于運算放大器U2的反相輸入端,運算放大器U2的反相輸入端和輸出端之間并聯電容C2,所述運算放大器U2的輸出端適于輸出狀態變量vy;
運算放大器U2的輸出端和運算放大器U3的反相輸入端之間串聯一阻值為36kΩ的電阻,運算放大器U3的反相輸入端和輸出端之間并聯另一阻值36kΩ的電阻,運算放大器U2和運算放大器U3的同相輸入端均接地;
所述運算放大器U3的輸出端適于輸出狀態變量–vy;以及
設置相應控制參數b=20、d=5、μ=0.1和v1=vxvz;
第三積分通道內包括第三積分器,其分別對應兩個輸入端,即
一輸入端適于接入狀態變量v2,且串聯另一電阻R/2后接于運算放大器U4的反相輸入端;
另一輸入端適于接入狀態變量vz,且串聯一電阻R/c后接于運算放大器U4的反相輸入端,運算放大器U4的反相輸入端和輸出端之間并聯電容C3,運算放大器U4的同相輸入端接地;
所述運算放大器U4的輸出端適于輸出狀態變量vz;以及
設置相應控制參數c=3和v2=–vxvy;并且
所述輸入端v1和v2分別對應乘法器M1和乘法器M2的輸出端,其中
乘法器M1的兩輸入端分別對應輸入端vx和vz;以及
乘法器M2的兩輸入端分別對應輸入端vx和-vy。
本發明的有益效果是,本發明涉及磁控憶阻類Lü系統超混沌隱藏吸引子產生電路及其構建方法,其在原有的Lü系統的第一方程中添加磁控憶阻項,即第一積分通道;第二方程中添加線性反饋項和外部激勵項,即第二積分通道、第三方程保持不變,實現了一種超混沌隱藏吸引子產生電路,并且該電路系統具有結構簡單、易于理論分析和電路集成,可呈現出點吸引子、周期極限環、準周期極限環、混沌吸引子和超混沌吸引子等隱藏振蕩現象,有較好的工程應用價值。
附圖說明
下面結合附圖和實施例對本發明進一步說明。
圖1(a)磁控憶阻對應的等效實現電路的電路圖;圖1(b)振蕩系統的電路圖;
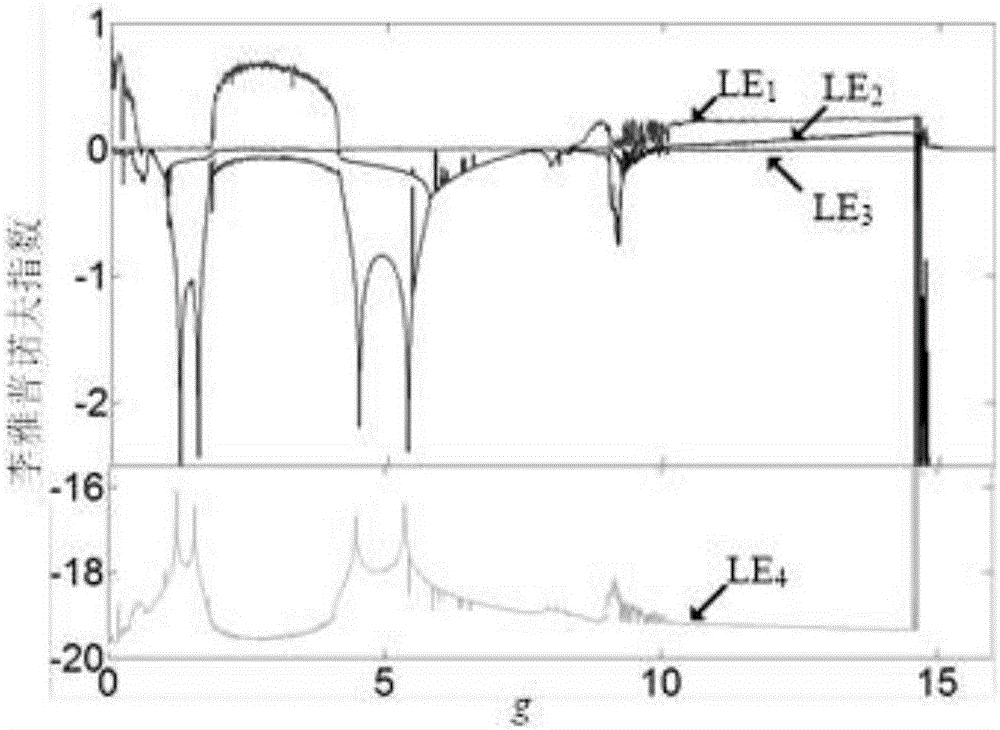
圖2磁控憶阻類Lü系統超混沌隱藏吸引子產生電路模型數值仿真得到的隨憶阻變化的李雅普諾夫指數圖,說明該電路存在復雜的動力學特性;
圖3磁控憶阻類Lü系統超混沌隱藏吸引子產生電路數值仿真得到的隱藏吸引子在x–z平面上的相軌圖,其中圖3(a)點吸引子;圖3(b)周期2極限環軌道;圖3(c)周期3極限環軌道;圖3(d)準周期極限環軌道;圖3(e)混沌軌道;圖3(f)超混沌軌道;
圖4磁控憶阻類Lü系統超混沌隱藏吸引子產生電路數值仿真得到的超混沌隱藏吸引子在4個相平面上的相軌圖,其中圖4(a)在x–z平面上;圖4(b)在x–y平面上;圖4(c)在x–w平面上;圖4(d)在w–z平面上;
圖5磁控憶阻類Lü系統超混沌隱藏吸引子產生電路實驗測量捕捉的隱藏吸引子在x–z平面上的相軌圖,其中圖5(a)點吸引子;圖5(b)周期2極限環軌道;圖5(c)周期3極限環軌道;圖5(d)準周期極限環軌道;圖5(e)混沌軌道;圖5(f)超混沌軌道;
圖6磁控憶阻類Lü系統超混沌隱藏吸引子產生電路實驗測量捕捉的超混沌隱藏吸引子在4個相平面上的相軌圖,其中圖6(a)在x–z平面上;圖6(b)在x–y平面上;圖6(c)在x–w平面上;圖6(d)在w–z平面上。
具體實施方式
現在結合附圖對本發明作進一步詳細的說明。這些附圖均為簡化的示意圖,僅以示意方式說明本發明的基本結構,因此其僅顯示與本發明有關的構成。
實施例1
如圖1(a)和圖1(b),本實施例1提供了一種超混沌隱藏吸引子產生電路,包括:振蕩系統和磁控憶阻對應的等效實現電路;其中所述振蕩系統適于通過與等效實現電路相連以呈現相應隱藏振蕩現象。
進一步,所述磁控憶阻等效實現電路包括:積分器,乘法器Ma、乘法器Mb,加法運算電路;其中所述磁控憶阻等效實現電路的輸入端對應的狀態變量–vy經過積分器運算后輸出狀態變量vw,且該狀態變量vw經過乘法器Ma后與狀態變量–vy通過乘法器Mb完成乘法運算后,再通過加法運算電路輸出–gW(vw)vy。
進一步,所述加法運算電路包括:與等效實現電路的輸入端相連的第一電阻R/gα,與第二乘法器輸出端相連的第二電阻R/gβ,且第一、第二電阻的另一端相連后作為等效實現電路的輸出端;其中設置相應控制參數α=4和β=0.18。
具體的,所述等效實現電路的連接方式為:其輸入端適于接入狀態變量–vy,且串聯電阻R/2后接運算放大器Ua的反相輸入端,運算放大器Ua的反相輸入端和輸出端之間并聯電容Ca,此時運算放大器Ua的輸出端適于輸出狀態變量vw;乘法器Ma的兩個輸入端都適于接入狀態變量vw,乘法器Ma的輸出端接乘法器Mb的一個輸入端;Mb的另一個輸入端適于接入狀態變量–vy,乘法器Mb的輸出端與所述等效實現電路輸出端之間串聯電阻R/gβ,狀態變量–vy與等效實現電路輸入端之間串聯電阻R/gα,此時憶阻輸出端輸出-gW(vw)vx;運算放大器Ua的同相輸入端接地;其中設置相應控制參數α=4和β=0.18。
所述磁控憶阻類Lü系統超混沌隱藏吸引子產生電路主電路如圖1所示,其中x,y,z和w為系統的四個狀態變量,vx,vy,vz和vw為系統對應電路的四個狀態變量并有如下關系,其中根據仿真結果考慮所用運放和乘法器的電壓范圍,對電壓狀態變量進行了一定的縮放
x=2vx/V,y=2vy/V,z=2vz/V,w=vw/V。
進一步,所述振蕩系統包括:第一、第二和第三積分通道;其中第一積分通道內包括第一積分器,其有兩個輸入端,即一輸入端適于接入狀態變量vx,且串聯一電阻R/a后接到運算放大器U1的反相輸入端;另一輸入端適于接入狀態變量–vy,且串聯另一電阻R/a后接于運算放大器U1的反相輸入端,該輸入端還串聯所述磁控憶阻器后接于運算放大器U1的反相輸入端,運算放大器U1的反相輸入端和輸出端之間并聯電容C1,且運算放大器U1的同相輸入端接地;所述運算放大器U1的輸出端適于輸出狀態變量vx;以及設置相應控制參數a=36;第二積分通道內包括第二積分器和一級反相器,其分別對應四個輸入端,即一輸入端適于接入狀態變量vx,且串聯一電阻R/d后接于運算放大器U2的反相輸入端;另一輸入端適于接入狀態變量v1,且串聯一電阻R/2后接于運算放大器U2的反相輸入端;第三輸入端適于接入狀態變量–vy,且串聯一電阻R/b后接于運算放大器U2的反相輸入端;第四輸入端適于接入外部激勵項–μ,且串聯一電阻2R后接于運算放大器U2的反相輸入端,運算放大器U2的反相輸入端和輸出端之間并聯電容C2,所述運算放大器U2的輸出端適于輸出狀態變量vy;運算放大器U2的輸出端和運算放大器U3的反相輸入端之間串聯一阻值為36kΩ的電阻,運算放大器U3的反相輸入端和輸出端之間并聯另一阻值36kΩ的電阻,運算放大器U2和運算放大器U3的同相輸入端均接地;所述運算放大器U3的輸出端適于輸出狀態變量–vy;以及設置相應控制參數b=20、d=5、μ=0.1和v1=vxvz;第三積分通道內包括第三積分器,其分別對應兩個輸入端,即一輸入端適于接入狀態變量v2,且串聯另一電阻R/2后接于運算放大器U4的反相輸入端;另一輸入端適于接入狀態變量vz,且串聯一電阻R/c后接于運算放大器U4的反相輸入端,運算放大器U4的反相輸入端和輸出端之間并聯電容C3,運算放大器U4的同相輸入端接地;所述運算放大器U4的輸出端適于輸出狀態變量vz;以及設置控制參數c=3和v2=–vxvy;并且所述輸入端v1和v2分別對應乘法器M1和乘法器M2的輸出端,其中乘法器M1的兩輸入端分別對應輸入端vx和vz;以及乘法器M2的兩輸入端分別對應輸入端vx和-vy。
三個積分通道與等效實現電路中通道所有相同標注的節點依次相連為一個四維振蕩系統。與振蕩系統中各積分電路各相同端口依次相連后,隨憶阻增益變化,可實現輸出周期極限環、準周期極限環、混沌吸引子和超混沌吸引子等隱藏振蕩現象。
實施例2
在實施例1基礎上,本實施例2還提供了一種超混沌隱藏吸引子產生電路的構建方法,包括如下步驟
步驟S1,建立磁控憶阻對應的等效實現電路;
步驟S2,建立振蕩系統;以及
步驟S3,將等效實現電路接入振蕩系統內以呈現相應隱藏振蕩現象。
進一步,所述磁控憶阻等效實現電路包括:積分器,乘法器Ma、乘法器Mb,加法運算電路;其中
所述磁控憶阻等效實現電路的輸入端對應的狀態變量–vy經過積分器的積分運算后輸出狀態變量vw,且該狀態變量vw經過乘法器Ma后與狀態變量–vy通過乘法器Mb完成乘法運算后,再通過加法運算電路輸出–gW(vw)vy。
進一步,所述加法運算電路包括:與等效實現電路的輸入端相連的第一電阻R/gα,與第二乘法器輸出端相連的第二電阻R/gβ,且第一、第二電阻的另一端相連后作為等效實現電路的輸出端;其中
設置相應控制參數α=4和β=0.18。
進一步,所述振蕩系統包括:第一、第二和第三積分通道;其中
第一積分通道內包括第一積分器,其有兩個輸入端,即
一輸入端適于接入狀態變量vx,且串聯一電阻R/a后接到運算放大器U1的反相輸入端;
另一輸入端適于接入狀態變量–vy,且串聯另一電阻R/a后接于運算放大器U1的反相輸入端,該輸入端還串聯所述磁控憶阻器后接于運算放大器U1的反相輸入端,運算放大器U1的反相輸入端和輸出端之間并聯電容C1,且運算放大器U1的同相輸入端接地;
此時所述運算放大器U1的輸出端適于輸出狀態變量vx;以及
設置相應控制參數a=36;
第二積分通道內包括第二積分器和一級反相器,其分別對應四個輸入端,即
一輸入端適于接入狀態變量vx,且串聯一電阻R/d后接于運算放大器U2的反相輸入端;
另一輸入端適于接入狀態變量v1,且串聯一電阻R/2后接于運算放大器U2的反相輸入端;
第三輸入端適于接入狀態變量–vy,且串聯一電阻R/b后接于運算放大器U2的反相輸入端;
第四輸入端適于接入外部激勵項–μ,且串聯一電阻2R后接于運算放大器U2的反相輸入端,運算放大器U2的反相輸入端和輸出端之間并聯電容C2,所述運算放大器U2的輸出端適于輸出狀態變量vy;
運算放大器U2的輸出端和運算放大器U3的反相輸入端之間串聯一阻值為36kΩ的電阻,運算放大器U3的反相輸入端和輸出端之間并聯另一阻值36kΩ的電阻,運算放大器U2和運算放大器U3的同相輸入端均接地;
所述運算放大器U3的輸出端適于輸出狀態變量–vy;以及
設置相應控制參數b=20、d=5、μ=0.1和v1=vxvz;
第三積分通道內包括第三積分器,其分別對應兩個輸入端,即
一輸入端適于接入狀態變量v2,且串聯另一電阻R/2后接于運算放大器U4的反相輸入端;
另一輸入端適于接入狀態變量vz,且串聯一電阻R/c后接于運算放大器U4的反相輸入端,運算放大器U4的反相輸入端和輸出端之間并聯電容C3,運算放大器U4的同相輸入端接地;
所述運算放大器U4的輸出端適于輸出狀態變量vz;以及
設置相應控制參數c=3和v2=–vxvy;并且
所述輸入端v1和v2分別對應乘法器M1和乘法器M2的輸出端,其中
乘法器M1的兩輸入端分別對應輸入端vx和vz;以及
乘法器M2的兩輸入端分別對應輸入端vx和-vy。
對實施例1和實施例2的具體實現原理進行展開說明如下:
數學建模:本發明基于磁控憶阻類Lü系統的數學模型
在式(1)中,x、y、z為3個狀態變量,a、b和c為3個控制參數。在式(1)基礎上,第一方程添加磁控憶阻項、第二方程添加線性反饋項和外部激勵項后,可建立磁控憶阻類Lü系統超混沌隱藏吸引子產生電路的無量綱方程為:
式(2)式有a、b、c、d和μ五個系統控制參數以及α和β兩個憶阻內部參數。在下面的分析中,設置a=36、b=20、c=3、d=5、μ=0.1、α=4和β=0.18,選擇憶阻增益g為磁控憶阻系統的唯一控制參數。因外部激勵項μ的存在,式(2)描述的憶阻系統不存在平衡點,因此該系統輸出的相軌圖均屬于隱藏吸引子。
在式(2)中,w為磁控憶阻內部無量綱狀態變量,且W(w)=(α+βw2)。基于運算放大器和模擬乘法器的純模擬電路可實現式(2)所描述的非線性動力學系統,其中,vx、vy、vz、vw分別代表4個積分電路通道的電容電壓狀態變量,其中根據(2)式數值仿真結果狀態變量的變化范圍太大,考慮到電路實現所用運放和乘法器的電壓范圍限制,對式(2)所描述的電壓狀態變量進行了一定的縮放:
x=2vx/V,y=2vy/V,z=2vz/V,w=vw/V (3)
RC為積分時間常數,且v1=vxvz和v2=–vxvy。因此,式(2)中的磁控憶阻類Lü系統超混沌隱藏吸引子產生電路原理圖如圖1所示,該電路狀態方程表示如下:
其中,本文選用的磁控憶阻器的數學模型為:
式(5)中,α和β為2個正實常數,vw為磁控憶阻的內部狀態變量,vy為憶阻的輸入電壓,iy為憶阻的輸出并用于第二積分通道中積分器的反向輸入。一種基于運算放大器和模擬乘法器實現的非理想磁控憶阻W(vw)的所述超混沌隱藏吸引子產生電路如圖1(a)所示,其中積分時間常數RC與圖1(b)的保持一致。至此,本發明構建了一種磁控憶阻類Lü系統超混沌隱藏吸引子產生電路的電路實現方案。
數值仿真如下:利用MATLAB仿真軟件平臺,可以對式(2)所描述的系統進行數值仿真分析。選擇龍格-庫塔(ODE45)算法對系統方程求解,可獲得此憶阻系統狀態變量的李雅普諾夫指數譜如圖2所示和隱藏吸引子相軌圖如圖3、4所示。當磁控憶阻增益g=16時,LE1=0、LE2=-2.982、LE3=-7.948、LE4=-8.077,由圖3(a)可見,磁控憶阻系統呈現點隱藏吸引子;當磁控憶阻增益g=1.7時,LE1=0、LE2=-0.06891、LE3=-0.594、LE4=-18.29,由圖3(b)可見,磁控憶阻系統呈現周期二隱藏極限環;當磁控憶阻增益g=5.96時,LE1=0、LE2=-0.2976、LE3=-0.299、LE4=-18.37,由圖3(c)可見,磁控憶阻系統呈現周期三隱藏極限環。當磁控憶阻增益g=7.95時,LE1=0、LE2=0、LE3=-0.1347、LE4=-18.83,由圖3(d)可見,磁控憶阻系統呈現準周期隱藏極限環。當磁控憶阻增益g=2.55時,LE1=0.6534、LE2=0、LE3=-0.06931、LE4=-19.53,由圖3(e)可見,磁控憶阻系統呈現隱藏混沌吸引子。當磁控憶阻增益g=13.4時,LE1=0.2411、LE2=0.1129、LE3=0、LE4=-19.32,由圖3(f)可見,磁控憶阻系統呈現隱藏超混沌吸引子。磁控憶阻系統的隱藏超混沌吸引子,對應的不同平面的MATLAB數值仿真相軌圖分別如圖4(a)(b)(c)(d)所示。毫無疑問在四維維度下的超混沌系統大大地提高了憶阻電路動力學特性的復雜性,對于憶阻系統在保密通信等方面的具有潛在的應用價值。由此表明,該電路可以通過調節電路憶阻增益參數值g產生不同的混沌信號,得到多種具有復雜動力學特性的混沌行為,實現了一種可行的新型憶阻超混沌隱藏吸引子信號發生器。
實驗驗證:本設計分立元件選用金屬膜電阻、精密可調電阻和獨石電容,分立器件選用供電電壓為±15V的OP07CP運算放大器和AD633JNZ模擬乘法器。實驗過程中,由Agilent Technologies DSO7054B數字存儲示波器完成實驗波形捕捉。其中,參考電阻和參考電容分別選擇為:R=36kΩ、C=100nF。此外,電阻Re和Rf是聯動可調的,其參數值分別為:Re=R/gα、Re=R/gβ。當增益g變化時,聯動可調電阻的參數值分別固定為:Re和Rf。憶阻系統(2)或是收斂到一個點的,或是周期的,或是準周期的,或是混沌的,或是超混沌的隱藏吸引子。隨著增益g變化的點、周期、準周期、混沌和超混沌隱藏吸引子在xz相平面上的投影如圖5所示。
對圖4(a)(b)(c)(d)數值仿真中的超混沌隱藏吸引子相軌圖進行了實驗驗證,實驗結果分別如圖6(a)(b)(c)(d)。
將圖5和6實驗測量結果與圖3和4數值仿真結果作比較,可發現兩者有著較好的一致性,由此驗證了憶阻系統的復雜動力學行為的存在性。該結果進一步證實了該系統可呈現出穩定的點吸引子、周期極限環、準周期極限環、混沌吸引子和超混沌引子等隱藏振蕩現象分析的正確性,電路實現一種磁控憶阻類Lü系統超混沌隱藏吸引子產生電路。
對比結果可以說明:實驗電路中觀測到的非線性現象與仿真結果具有較好的一致性,可以驗證理論分析和數值仿真的正確性。因此,本發明所構建的一種磁控憶阻類Lü系統超混沌隱藏吸引子產生電路具有科學的理論依據和物理上的可實現性,可對混沌電路研究到相關領域工程應用起到積極的推動作用。
以上述依據本發明的理想實施例為啟示,通過上述的說明內容,相關工作人員完全可以在不偏離本項發明技術思想的范圍內,進行多樣的變更以及修改。本項發明的技術性范圍并不局限于說明書上的內容,必須要根據權利要求范圍來確定其技術性范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!