一種考慮多普勒效應與IQ不平衡的多徑信道估計方法與流程
本發明涉及OFDM系統領域,更具體地,涉及一種考慮多普勒效應與IQ不平衡的多徑信道估計方法。
背景技術:
隨著科學技術的發展,人們對下一代寬帶無線通信系統有著更高速率、更高穩定性、更高移動性的同時減少成本、減少功率消耗的要求。而為了滿足高速率的要求,未來的技術發展將應用更高的載波頻率和使用更高階的信號星座圖(例如64QAM),這使得寬帶無線通信系統對于系統的移動性和I/Q不平衡變得更加敏感,I/Q不平衡在直接變頻接收機中體現得尤為明顯。
除了I/Q不平衡,系統的移動性(多普勒效應)也破壞了每個OFDM符號子載波的正交性,引入inter-carrier干擾(ICI)。在更高速率、更高載波頻率、更大OFDM塊持續時間的情況下干擾變得更多且更嚴重。因此本發明針對系統的移動性和I/Q不平衡提出新的信道估計方法,并根據信道估計結果對信號進行相應的補償,最后實現信號可靠性的提高。
為了減少前面提到的接收前端的I/Q不平衡,準確得估計相應的I/Q不平衡參數就至為重要,然而在多徑衰落的情況下,I/Q不平衡參數受到信道沖激響應(channel impulse response-CIR)的影響,使得對I/Q不平衡參數的估計變成一個更加有挑戰性的工作。
在設定信道的沖激響應h(n)在信號發送的過程中保持不變,則發送的OFDM信號sm和接收到的信號ym在去除循環前綴后之間的關系為ym=Uh*sm+wm,其中Uh表示信道的沖擊響應h(n)組成的N×N循環矩陣,h=[h(0),...,h(L-1)],L表示多徑信道的長度。由于Uh是循環矩陣的關系,因此可以對Uh進行相應的一些變化:Uh=FH*G*F,其中F為DFT矩陣,而G則是一個對角矩陣,且diag(G)=[g1,g2,...,gN]T與h(n)的DFT變換相同。
當考慮系統的移動性時,則信道的沖激響應h(n)在信號發送的過程中就不能保持不變了,這樣導致相鄰兩個符號進入信道時信道的沖激響應的值不相同,再根據發送的OFDM信號sm和接收到的信號ym在去除循環前綴后之間的關系表示為ym=Uh*sm+wm,這時的Uh就不再是一個循環矩陣,此時再對Uh進行相應的變化:Uh=FH*G*F,這時的G不再是一個對角矩陣。
然而,G的形式跟多普勒效應有著直接的關系,當多普勒偏移不存在時,G的主對角線不為零,其他的次對角線為0,當加入多普勒偏移后,次對角線也不為零,且多普勒偏移越嚴重,不為0的次對角線的條數就越多,如果只對G的主對角線進行估計的話則最后通過補償后的信號的誤碼率就會較大,正確估計主、次對角線上的數據后對其進行補償則信號的誤碼率就會減少。
技術實現要素:
本發明的目的在于改進現有技術忽略多普勒效應對信道的影響,綜合多普勒效應、發送端和接收端的I/Q不平衡影響來實現對多徑信道比較準確的估計。
為實現以上發明目的,采用的技術方案是:
一種考慮多普勒效應與IQ不平衡的多徑信道估計方法,包括以下步驟:
S1.設多徑信道發送端的輸入信號為sm,接收端對接收到的信號去除循環前綴后的輸出信號為rm,則輸入信號和輸出信號之間的關系表示為:
rm=(uturUh+vt*vrUh*)sm+(vturUh+ut*vrUh*)sm*+wm (1)
由于Uh=FH*G*F,式(1)進一步表示為:
rm=(uturFH×G×F+vt*vrFH×G×F*)sm+(vturFH×G×F+ut*vrFH×G×F*)sm*+wm (2)
其中,*表示數值或矩陣的共軛,H表示矩陣的共軛轉置;ut、vt表示發送端發送的過程中加入的I/Q不平衡參數,ur、vr表示接收端接收的過程中加入的I/Q不平衡參數,Uh表示表示信道的沖擊響應h(n)組成的N×N循環矩陣;F為DFT矩陣,G為包含三對角線的矩陣;wm為傳輸過程中引入的高斯白噪聲;
S2.將矩陣G進行拆解:
其中
S3.將FH×B1×F、FH×B2×F近似為單位陣,則式(2)可進一步表示為:
rm=[k1(Uh1+Uh+Uh2)+k2(Uh1+Uh+Uh2)*]p+[k3(Uh1+Uh+Uh2)+k4(Uh1+Uh+Uh2)*]p*+wm
其中,k1=utur,k2=vt*vr,k3=vtur,k4=ut*vr,Uh1=FH×H1×F,Uh=FH×G0×F,Uh2=FH×H2×F;
由于Uh1、Uh、Uh2均為循環矩陣,則存在Uh×p=P×h,其中p表示rm,h表示信道參數[h(0),...,h(L-1)],L表示多徑信道的長度;P表示序文向量p=[p0,p1,...,pN]T,N為序文向量的長度,則rm可進一步表示為:
rm=P(k1h1+k2h1*)+P*(k3h1*+k4h1*)+P(k1h+k2h*)+P*(k3h+k4h*)+P(k1h2+k2h2*)+P*(k3h2+k4h2*)+wm
S4.構造矩陣Pre=[P P*P P*P P*],設c=[c1T c2T c3T c4T c5T c6T]T,其中c1=k1h1+k2h1*;c2=k3h1+k4h1*;c3=k1h+k2h*;c4=k3h+k4h*;c5=k1h2+k2h2*;c6=k3h2+k4h2*;
則rm可表示為:rm=Pre×c+wm,由基于交替最小二乘法可得:
c=(PreH×Pre)-1×PreH×rm;
S5.定義K=[k1,k2,k3,k4]T,設令c=H×K+wm,根據基于交替最小二乘法可得K的估計值:Kls=(HH×H)-1×HH×c;
S6.將c1=k1h1+k2h1*的實部和虛部分離出來:
Re(c1)=[Re(k1)+Re(k2)]×Re(h1)+[Im(k1)-Im(k2)]×Im(h1);
Im(c1)=[Im(k1)+Im(k2)]×Re(h1)+[Re(k1)+Re(k2)]×Im(h1);
同理可得c2、c3、c4、c5、c6的表達式,則矩陣C可表示為:
C=[Re(c1)T Im(c1)T Re(c2)T Im(c2)T Re(c3)T Im(c3)T Re(c4)T Im(c4)T Re(c5)TIm(c5)T Re(c6)T Im(c6)T]T;
S7.令HLs=[Re(h1) Im(h1) Re(h) Im(h) Re(h2) Im(h2)]T;
將步驟S5獲得的Kls經過實虛部分離后得到KLS表示如下:
S8.則表達式c=H×K+Wm可表達為C=HLs×KLs+wm,根據基于交替最小二乘法可得:HLs=(KLsT×KLs)-1×KLsT×C;
S9.根據求解得到的HLs實現對信道參數h1、h、h2的估計。
優選地,在估計得到信道參數h1、h、h2后,根據信道參數h1、h、h2對信號進行相應的補償。
優選地,所述ut=cosθt+jαtsinθt,vt=αtcosθt+jsinθt。
優選地,所述ur=cosθr-jαrsinθr,vr=αrcosθr+jsinθr。
與現有技術相比,本發明的有益效果是:
本發明提供的信道估計方法將信道的多普勒效應與IQ不平衡考慮在內,并利用基于交替最小二乘法對信道的參數進行估計,在進行估計的過程中,對矩陣G的估計是考慮到其主、次對角線上的數據的,因此估計結果與實際的結果是非常接近的,本發明提供的方法能夠以較高的準確性來對信道實質的參數進行估計。
附圖說明
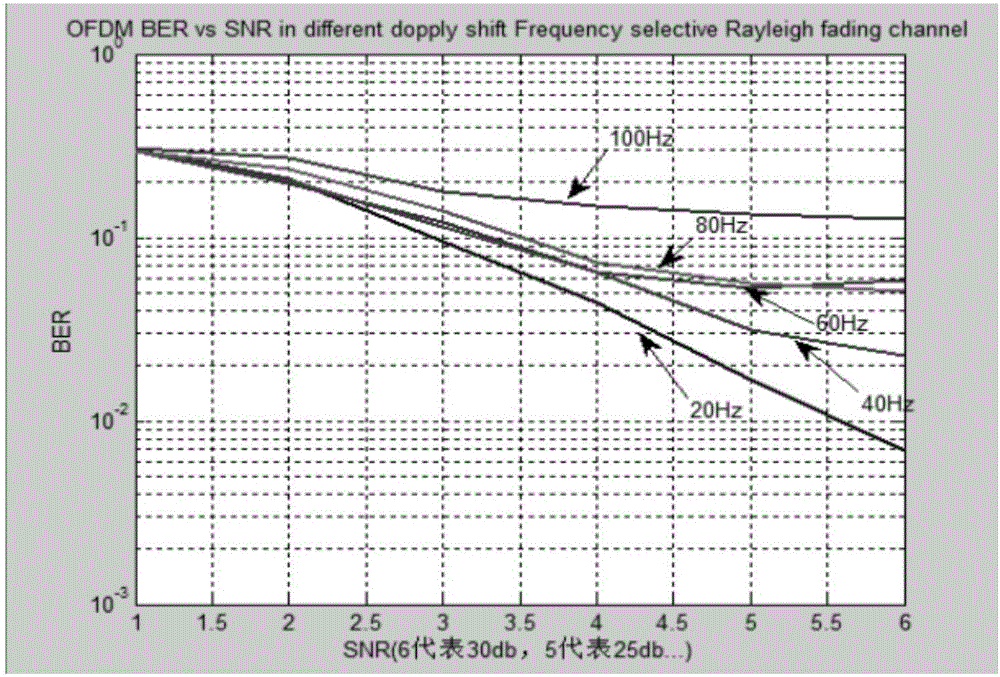
圖1為不同多普勒頻偏效應下的誤碼率示意圖。
圖2為原始信號經過調制后、進入信道和經過信道均衡后的星座圖。
圖3為實驗的結果示意圖。
圖4為OFDM工作的流程圖。
圖5為信道估計的流程圖。
具體實施方式
附圖僅用于示例性說明,不能理解為對本專利的限制;
以下結合附圖和實施例對本發明做進一步的闡述。
實施例1
如圖4所示,OFDM系統在進行數據的發送與接收時,一般包括以下步驟:
S1.隨機生成序文,將生成的序文進行16QAM調制得到調制信號;
S2.將調制后的信號進行IFFT變換,經過變換的信號升頻至2.4GHz,在升頻的過程加入發送端的I/Q不平衡參數ut、vt;(ut=cosθt+jαtsinθt,vt=αtcosθt+jsinθt)
S3.生成多徑信道,然后將升頻后的信號接入信道得到輸出信號,設多徑信道的長度為9,控制信道的多普勒頻偏為0Hz—100Hz測量在多個值下的情況;
S4.將從信道出來的信號降頻,在降頻過程中加入接收端的I/Q不平衡參數ur、vr,(ur=cosθr-jαrsinθr,vr=αrcosθr+jsinθr),再將信號進行FFT變換。其中,圖1為不同多普勒頻偏效應下的誤碼率示意圖。圖2為原始信號經過調制后、進入信道和經過信道均衡后的星座圖。
因此,要進行信道估計獲得信道實際上的信道參數時,則必需知道ut、vt、ur、vr、發送端的輸入信號sm、接收端的輸出信號rm。
在以上基礎上,如圖5所示,本發明提供的方法主要包括以下步驟:
第一步、設多徑信道發送端的輸入信號為sm,接收端對接收到的信號去除循環前綴后的輸出信號為rm,則輸入信號和輸出信號之間的關系表示為:
rm=(uturUh+vt*vrUh*)sm+(vturUh+ut*vrUh*)sm*+wm (1)
由于Uh=FH*G*F,式(1)進一步表示為:
rm=(uturFH×G×F+vt*vrFH×G×F*)sm+(vturFH×G×F+ut*vrFH×G×F*)sm*+wm (2)
其中,*表示數值或矩陣的共軛,H表示矩陣的共軛轉置;ut、vt表示發送端發送的過程中加入的I/Q不平衡參數,ur、vr表示接收端接收的過程中加入的I/Q不平衡參數,Uh表示表示信道的沖擊響應h(n)組成的N×N循環矩陣;F為DFT矩陣,G為包含三對角線的矩陣;wm為傳輸過程中引入的高斯白噪聲;
第二步、將矩陣G進行拆解:
其中
第三步、將FH×B1×F、FH×B2×F近似為單位陣,則式(2)可進一步表示為:
rm=[k1(Uh1+Uh+Uh2)+k2(Uh1+Uh+Uh2)*]p+[k3(Uh1+Uh+Uh2)+k4(Uh1+Uh+Uh2)*]p*+wm
其中,k1=utur,k2=vt*vr,k3=vtur,k4=ut*vr,Uh1=FH×H1×F,Uh=FH×G0×F,Uh2=FH×H2×F;
由于Uh1、Uh、Uh2均為循環矩陣,則存在Uh×p=P×h,其中p表示rm,h表示信道參數[h(0),...,h(L-1)],L表示多徑信道的長度;P表示序文向量p=[p0,p1,...,pN]T,N為序文向量的長度,則rm可進一步表示為:
rm=P(k1h1+k2h1*)+P*(k3h1*+k4h1*)+P(k1h+k2h*)+P*(k3h+k4h*)+P(k1h2+k2h2*)+P*(k3h2+k4h2*)+wm
第四步、構造矩陣Pre=[P P*P P*P P*],設c=[c1T c2T c3T c4T c5T c6T]T,其中c1=k1h1+k2h1*;c2=k3h1+k4h1*;c3=k1h+k2h*;c4=k3h+k4h*;c5=k1h2+k2h2*;c6=k3h2+k4h2*;
則rm可表示為:rm=Pre×c+wm,由基于交替最小二乘法可得:
c=(PreH×Pre)-1×PreH×rm;
第五步、定義K=[k1,k2,k3,k4]T,設
令c=H×K+wm;
根據基于交替最小二乘法可得K的估計值:Kls=(HH×H)-1×HH×c;
第六步、將c1=k1h1+k2h1*的實部和虛部分離出來:
Re(c1)=[Re(k1)+Re(k2)]×Re(h1)+[Im(k1)-Im(k2)]×Im(h1);
Im(c1)=[Im(k1)+Im(k2)]×Re(h1)+[Re(k1)+Re(k2)]×Im(h1);
同理可得c2、c3、c4、c5、c6的表達式,則矩陣C可表示為:
C=[Re(c1)T Im(c1)T Re(c2)T Im(c2)T Re(c3)T Im(c3)T Re(c4)T Im(c4)T Re(c5)TIm(c5)T Re(c6)T Im(c6)T]T;
第七步、令HLs=[Re(h1) Im(h1) Re(h) Im(h) Re(h2) Im(h2)]T;
將步驟S5獲得的Kls經過實虛部分離后得到KLS表示如下:
第八步、則表達式c=H×K+Wm可表達為C=HLs×KLs+wm,根據基于交替最小二乘法可得:HLs=(KLsT×KLs)-1×KLsT×C;
第九步、根據求解得到的HLs實現對信道參數h1、h、h2的估計。
上述方案中,本發明提供的信道估計方法將信道的多普勒效應與IQ不平衡考慮在內,并利用基于交替最小二乘法對信道的參數進行估計,在進行估計的過程中,對矩陣G的估計是考慮到其主、次對角線上的數據的,因此估計結果與實際的結果是非常接近的,本發明提供的方法能夠以較高的準確性來對信道實質的參數進行估計。
實施例2
本實施例在實施例1的基礎上,進行了具體的仿真實驗,圖3為實驗的結果示意圖。如圖3所示,當對矩陣G進行估計時,若只對其主對角線進行估計,那么得出的信道參數用于平衡信道后,信號的誤碼率是低于對主、次對角線估計得到的信道參數補償后的誤碼率的。因此本發明提供的方法能夠起到改善信道誤碼率的效果。
顯然,本發明的上述實施例僅僅是為清楚地說明本發明所作的舉例,而并非是對本發明的實施方式的限定。對于所屬領域的普通技術人員來說,在上述說明的基礎上還可以做出其它不同形式的變化或變動。這里無需也無法對所有的實施方式予以窮舉。凡在本發明的精神和原則之內所作的任何修改、等同替換和改進等,均應包含在本發明權利要求的保護范圍之內。
- 還沒有人留言評論。精彩留言會獲得點贊!