一種基于最大最小特征值之差的協作頻譜感知方法與流程

本發明屬于認知無線電技術領域，特別涉及一種用于認知無線電系統的基于最大最小特征值之差的協作頻譜感知方法。

背景技術：

隨著無線通信業務的快速增長，無線頻譜資源日趨緊張。由于現有的頻譜采用獨占的分配方式，只有主用戶才可以使用授權頻譜，即使主用戶處于空閑狀態其他用戶也無法使用該頻段。為了改善這一現象，認知無線電也就應運而生，作為一種智能的頻譜共享技術，能檢測出主用戶未被使用的空閑頻段，不影響主用戶的情況下允許其他用戶接入，從而提高頻譜的利用率。

頻譜感知技術是認知無線電的關鍵技術。常用的頻譜感知技術包括能量檢測方法、匹配濾波檢測法和循環平穩特征檢測法。由于能量檢測實現簡單，不需要知道主用戶信號的任何先驗知識，使得能量檢測成為最普遍的檢測方法之一。但是由于噪聲的影響，對微弱信號檢測能力較差，設定門限時需要知道噪聲方差，而現實環境中噪聲方差是時變的、不確定的。匹配濾波檢測是一種性能最優的檢測方法，但是必須已知主用戶的先驗信息，對不同類型的發射機信號，需要設計不同的匹配濾波器，增加了系統的復雜度。循環平穩特征檢測抗信噪性強，檢測性能好，但是計算量大，檢測時間長，降低了系統的準確度。

考慮到以上經典算法的諸多缺點。近年來，隨機矩陣理論(RMT)逐漸被應用于頻譜感知領域，許多優秀算法也相繼被提出，包括最大最小特征值算法(MME)、能量-最小特征值算法(EME)、基于協方差的特征值的幾何平均與算術平均值之比(AGM)算法。這些算法都有效的避免了噪聲不確定性帶來的影響，但大都采用漸近近似分布規律，所得到閾值表達式需進一步提高。

技術實現要素：

本發明的目的在于克服現有技術的缺點與不足，提供一種認知無線電系統中基于最大最小特征值之差的協作頻譜感知方法。本方法基于新的統計量，將最大最小特征值之差作為檢測統計量；所使用的門限值表達式是基于最小特征值的分布規律計算得到的，最小特征值的分布函數不基于漸近假設。推導所得的門限值表達式是基于虛警概率和協作用戶數的函數，在低樣本數的情況下可以更加準確的判斷出主用戶是否存在，既提高了系統的性能又降低了系統的復雜度。

本發明的目的通過下述技術方案實現：

(1)M個認知用戶對同一主用戶協同檢測，每個認知用戶接收到的信號進行N次采樣，則可以組成M×N的接收信號矩陣Y。

(2)根據上述接收信號矩陣Y，計算樣本協方差矩陣其中Y^H為信號矩陣Y的厄密特轉置矩陣。

(3)計算樣本協方差矩陣的特征值，并選擇其中的最大特征值λ_max與最小特征值λ_min之差作為檢測統計量Γ。

(4)算法理論基礎一

對于歸一化的樣本協方差矩陣最小特征值的概率密度函數可以表示為：

式中：

$C={\[\underset{m=1}{\overset{M}{\Π}}(N-m)!(M-m)!\]}^{-1}$

M_λ是一個(M-1)×(M-1)階的矩陣，矩陣中的元素可以表示為：

式中Γ(·,·)表示不完全Gamma函數：

R_Y′(N)最小特征值的分布函數可以表示為：

$F_{min}\left(\mathrm{\λ}\right)={\∫}_{-\mathrm{\∞}}^{\mathrm{\λ}}{f}_{min}\left(t\right)dt={\∫}_0^{\mathrm{\λ}}{f}_{min}\left(t\right)dt$

(5)算法理論基礎二

設隨機矩陣X中的元素滿足零均值獨立同分布，方差為σ²/N，則當M→∞,N→∞，且M/N＝β時，XX^H的ESD幾乎一定收斂到M-P律，它的概率密度函數為：

$f_{\mathrm{\β}}\left(x\right)={(1-{\mathrm{\β}}^{-1})}^{+}\mathrm{\δ}\left(x\right)+\frac{\sqrt{{(x-{\mathrm{\η}}_1)}^{+}{({\mathrm{\η}}_2-x)}^{+}}}{2\mathrm{\π}\mathrm{\β}x}$

式中：分別為最小特征值和最大特征值的收斂值，即λ∈[η₁,η₂]，σ²為方差，(a)⁺為0和a中去較大者，δ(x)為單位沖擊函數。

(6)根據算法理論基礎二，協方差矩陣的最大特征值收斂值可以表示為根據給定的虛警概率值，可以推導出判決閾值表達式：

所以，其中表示F_min(t)的反函數，σ²是噪聲方差。如果噪聲已知時，直接將其代入到閾值表達式中；若噪聲方差未知時，通過最小特征值對噪聲方差實時估計，將估計得到的噪聲方差代入閾值表達式中，為了減少利用最小特征值估計噪聲方差帶來的誤差，噪聲方差表達式可以表示為

(7)將得到的檢測統計量Γ與判決門限γ進行比較，當檢測統計量大于等于判決門限時，即Γ≥γ，表明當前頻譜資源被主用戶占用，認知用戶不能利用該頻譜資源。當檢測統計量小于判決門限時，即Γ＜γ，認為當前頻譜資源空閑，認知用戶可以利用該頻譜資源。

本發明相對于現有技術具有如下的優點及效果：

(1)以往基于隨機矩陣頻譜感知算法都需要在采樣點非常多的情況下實現，而本發明所提出的算法不需要大量的采樣點，降低了計算的復雜度以及設計檢測器所需的成本。

(2)以往的隨機矩陣頻譜感知算法由于需要的采樣點多，采用的檢測分布函數大都是采用大維漸近的分布理論，計算出來的閾值表達式不夠精確，降低了對主用戶的檢測準確度。本發明提供的檢測分布函數不是基于大維情況下的分布規律，而是根據采樣點較少時最小特征值的分布規律，其概率密度函數不基于漸近假設，推導所得的閾值表達式是基于虛警概率的函數，在小樣本情況下，其優越性得到了驗證。

附圖說明

圖1是本發明的頻譜感知方法的流程框圖；

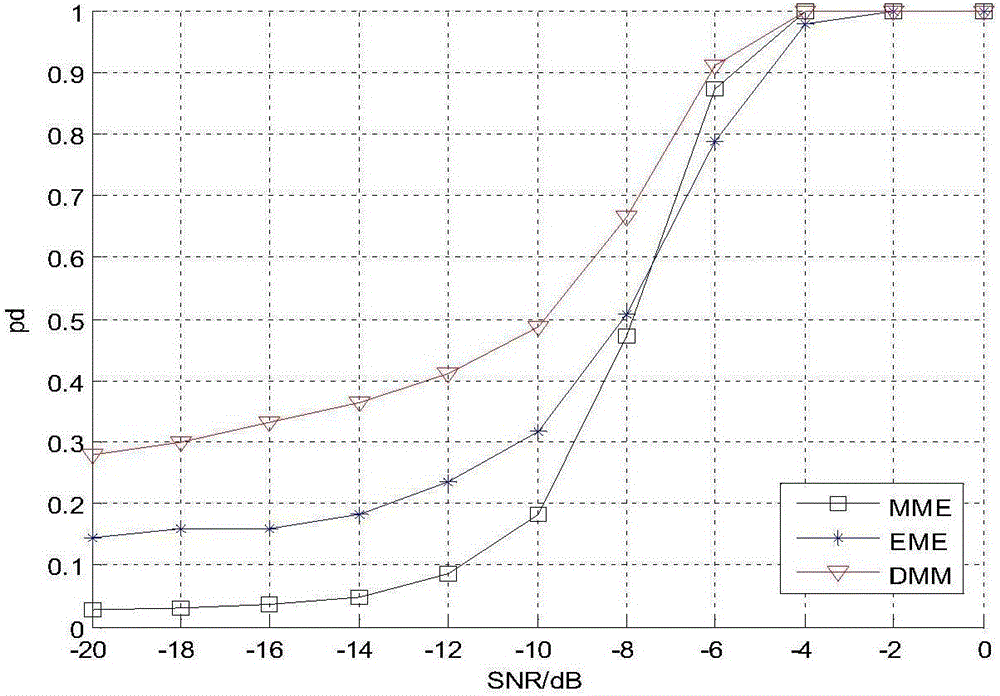
圖2是本發明與其他兩種算法的檢測概率-信噪比之間的關系對比圖。

具體實施方式

下面結合實施例及附圖對本發明作進一步詳細的描述，但本發明的實施方式不限于此。

實施例內容如下：

圖1為本實施例的一種基于最小特征值的協作頻譜感知方法流程圖

步驟1，計算接收信號矩陣Y：

M個認知用戶對主用戶協同檢測，對接收到的信號進行采樣得到信號X,每個認知用戶分別對接收到的信號采樣N次。

M個認知用戶采樣N次的信號矩陣可以表示為Y＝[y₁y₂…y_M]^T

其中y₁表示第一個認知用戶采樣N次所組成的一維向量。

步驟2，根據接收信號矩陣Y，計算樣本協防差矩陣

${\hat{R}}_y\stackrel{\mathrm{\Δ}}{=}\frac{1}{N}\underset{n=0}{\overset{N-1}{\Σ}}y\left(n\right)y^H\left(n\right)=\frac{1}{N}{\mathrm{YY}}^H,$

其中，(·)^H表示矩陣的厄密特轉置。

步驟3，計算樣本協方差的特征值λ₁,λ₂,…,λ_M，其中λ_i是協方差矩陣的第i個特征值，其中M為認知用戶的個數，選擇最大特征值與最小特征值的差λ_max-λ_min作為統計量Γ。

步驟4，單個認知用戶對主用戶信號進行檢測的情況，可以用統計學中的二元假設模型來表示，假設H₀表示主用戶不存在，H₁表示授權用戶存在，計算當主用戶存在時的判決閾值γ。

步驟5，求解分布函數表達式。對于歸一化的樣本協方差矩陣最小特征值的概率密度函數可以表示為：

式中：

$C={\[\underset{m=1}{\overset{M}{\Π}}(N-m)!(M-m)!\]}^{-1}$

M_λ是一個(M-1)×(M-1)階的矩陣，矩陣中的元素可以表示為：

式中Γ(·,·)表示不完全Gamma函數：

R_Y′(N)最小特征值的分布函數可以表示為：

$F_{min}\left(\mathrm{\λ}\right)={\∫}_{-\mathrm{\∞}}^{\mathrm{\λ}}{f}_{min}\left(t\right)dt={\∫}_0^{\mathrm{\λ}}{f}_{min}\left(t\right)dt$

步驟6，隨機矩陣最大特征值漸近分布規律。設隨機矩陣X中的元素滿足零均值獨立同分布，方差為σ²/N，則當M→∞,N→∞，且M/N＝β時，XX^H的ESD幾乎一定收斂到M-P律，它的概率密度函數為：

$f_{\mathrm{\β}}\left(x\right)={(1-{\mathrm{\β}}^{-1})}^{+}\mathrm{\δ}\left(x\right)+\frac{\sqrt{{(x-{\mathrm{\η}}_1)}^{+}{({\mathrm{\η}}_2-x)}^{+}}}{2\mathrm{\π}\mathrm{\β}x}$

式中：分別為最小特征值和最大特征值的收斂值，即λ∈[η₁,η₂]，σ²為方差，(a)⁺為0和a中去較大者，δ(x)為單位沖擊函數。

所以，協方差矩陣的最大特征值收斂值可以表示為

步驟7，求解閾值的表達式。

所以，其中表示F_min(t)的反函數，σ²是噪聲方差。如果噪聲已知時，直接將其代入到閾值表達式中；若噪聲方差未知時，通過最小特征值對噪聲方差實時估計，將估計得到的噪聲方差代入閾值表達式中，為了減少利用最小特征值估計噪聲方差帶來的誤差，噪聲方差表達式可以表示為

步驟8，判斷主用戶是否存在，如果統計量Γ大于或等于閾值γ，表示主用戶存在；否則，主用戶不存在。

步驟9，圖2是最大最小特征值(MME)、平均能量與最小特征值(ED-ME)以及本發明最大最小特征值之差(DMM)的檢測概率與信噪比之間的關系曲線對比圖。本實施例采用的是蒙特卡洛仿真，主用戶發射機的信號是BPSK調制信號，仿真過程中所涉及的參數有信號的采樣頻率f_s為1，采樣點數N為150，協作認知用戶的個數為4，虛警概率P_f為0.1。仿真結果表明本發明算法(DMM)在相同的環境下優于MME算法和EME算法，特別是在低信噪比時DMM算法明顯優于MME算法和EME算法。

上述實施例為本發明較佳的實施方式，但本發明的實施方式并不受上述實施例的限制，其他的任何未背離本發明的精神實質與原理下所作的改變、修飾、替代、組合、簡化，均應為等效的置換方式，都包含在本發明的保護范圍之內。