一種重疊頻分復用調制方法、裝置及系統與流程

本發明涉及通信領域，具體涉及一種重疊頻分復用調制方法、裝置及重疊頻分復用系統。

背景技術：

頻分復用FDM(Frequency Division Multiplexing)是一種讓多個占據較窄帶寬的信號共享一個較寬帶寬的技術。如圖1所示，各被利用的信號帶寬分別為B1，B2，B3，B4，….，當然它們也可以占據相同帶寬，△B為最小保護帶寬，實際保護帶寬可以寬裕一些。△B應大于所使用的解復用濾波器的過渡帶寬加上系統的最大頻率漂移及信道的最大頻率擴散量。這是最常見的頻分復用技術，現有的絕大多數的廣播系統、通信系統和雷達系統等都采用的是這種技術。這種技術的最大特點是被利用的信號頻譜之間是相互隔離的，不會存在相互干擾。

因此，傳統的觀點是相鄰信道之間在頻率域上不重疊，以避免相鄰信道之間產生干擾，但這種技術制約了頻譜效率的提高。現有技術的頻分復用技術的觀點是各信道之間不但不需要相互隔離，而且可以有很強的相互重疊，如圖2所示，現有技術將信道之間的重疊視為一種新的編碼約束關系，并根據該約束關系提出了相應的調制和解調技術，因此稱之為重疊頻分復用，這種技術使得頻譜效率隨重疊次數K成比例的增加，其中圖2中是K＝3的情況。

理論上，當采用重疊頻分復用技術進行數據傳輸時，重疊次數K可無限地增加，因此頻譜效率也可無限地增加，但在實驗室研究階段卻發現隨著重疊次數K的增加，雖然頻譜效率得到增加，但是傳輸功率隨之也增長，而傳輸功率的增長反過來在一定程度上也限制了重疊次數K的增加，從而也限制了頻譜效率的增加。

技術實現要素：

本申請提供一種重疊頻分復用調制方法、裝置及系統。

根據第一方面，一種實施例中提供一種重疊頻分復用調制方法，包括以下步驟：

根據設計參數生成一個頻域內波形平滑的初始包絡波形，其中，所述初始包絡波形為泰勒窗包絡波形或其演變窗函數的包絡波形；

根據重疊復用次數將所述初始包絡波形在頻域上按預定的頻譜間隔進行移 位，得到各子載波包絡波形；

將輸入的數字信號序列轉換成正負符號序列；

將所述正負符號序列中的符號與各自對應的子載波包絡波形相乘，得到各子載波的調制包絡波形；

將所述各子載波的調制包絡波形在頻域上進行疊加，得到頻域上的復調制包絡波形；

將所述頻域上的復調制包絡波形進行變換，得到時域上的復調制包絡波形。

根據第二方面，一種實施例中提供一種重疊頻分復用調制裝置，包括：

波形生成模塊，用于生成一個頻域內波形平滑的初始包絡波形，其中所述波形生成模塊生成的初始包絡波形為泰勒窗包絡波形或其演變窗函數的包絡波形；

移位模塊，用于根據重疊復用次數將所述初始包絡波形在頻域上按預定的頻譜間隔進行移位，得到各子載波包絡波形；

轉換模塊，用于將輸入的數字信號序列轉換成正負符號序列；

乘法模塊，用于將所述正負符號序列中的符號與各自對應的子載波包絡波形相乘，得到各子載波的調制包絡波形；

疊加模塊，用于將所述各子載波的調制包絡波形在頻域上進行疊加，得到頻域上的復調制包絡波形；

變換模塊，用于將所述頻域上的復調制包絡波形進行變換，得到時域上的復調制包絡波形。

根據第三方面，一種實施例中提供一種重疊頻分復用系統，包括發射機和接收機；

所述發射機包括：

上述的重疊頻分復用調制裝置，用于調制生成攜帶輸出信號序列的復調制包絡波形；

發射裝置，用于將所述復調制包絡波形發射到接收機；

所述接收機包括：

接收裝置，用于接收所述復調制包絡波形；

重疊頻分復用解調裝置，用于對接收的復調制包絡波形進行解調，最終經過譯碼得到最終的輸入比特序列。

依據上述實施例的重疊頻分復用調制方法、裝置及系統，由于生成的初始包絡波形為泰勒窗或其演變窗函數包絡波形，其在頻域內波形平滑，相應地，其在時域內能量集中且持續時間較短，因此經過其調制形成的復調調包絡波形 在時域能量集中且持續時間較短，因此其頻譜利用率高，信號傳輸速率也高，并且只需要較低的傳輸功率，被解調時具有較低的誤碼率。

附圖說明

圖1為傳統頻分復用技術中各信號共享一個較寬帶寬的波形示意圖；

圖2為現有重疊頻分技術中各信道之間重疊后形成的編碼約束關系示意圖；

圖3為本申請一種實施例中重疊頻分復用系統的結構示意圖；

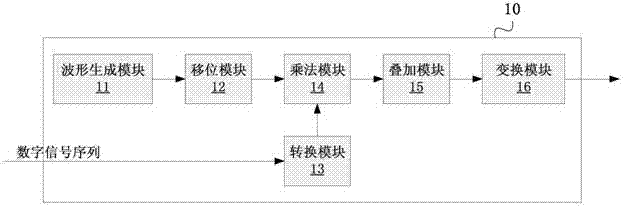
圖4為本申請一種實施例中重疊頻分復用調制裝置的結構示意圖；

圖5為本申請一種實施例中接收裝置的結構示意圖；

圖6為本申請一種實施例中重疊頻分復用解調裝置的結構示意圖；

圖7為本申請一種實施例中重疊頻分復用調制方法的流程示意圖；

圖8為本申請一種實施例中輸出信號序列確定方法的流程示意圖；

圖9為本申請一種實施例中K路波形復用的疊加原理示意圖；

圖10為本申請一種實施例中泰勒窗包絡波形的三種頻域圖；

圖11為本申請一種實施例中以泰勒窗包絡波形作為初始包絡波形調制得到的各子載波包絡波形和復調制包絡波形的三種頻域圖；

圖12為本申請一種實施例中以泰勒窗包絡波形作為初始包絡波形調制得到的復調制包絡波形的三種時域圖；

圖13為本申請一種實施例中3路波形復用的疊加原理示意圖；

圖14為本申請一種實施例中矩形窗包絡波形的頻域圖；

圖15為本申請一種實施例中以矩形窗包絡波形作為初始包絡波形調制得到的復調制包絡波形的時域圖；

圖16為本申請一種實施例中以矩形窗包絡波形作為初始包絡波形調制得到的復調制包絡波形的時域圖；

圖17為本申請一種實施例中輸入-輸出關系圖；

圖18為本申請一種實施例中節點狀態轉移圖；

圖19為本申請一種實施例中以泰勒窗一階導包絡波形作為初始包絡波形調制得到的復調制包絡波形的三種頻域圖；

圖20為本申請一種實施例中以泰勒窗一階導包絡波形作為初始包絡波形調制得到的各子載波包絡波形和復調制包絡波形的三種頻域圖

圖21為本申請一種實施例中以泰勒窗一階導包絡波形作為初始包絡波形調制得到的復調制包絡波形的三種時域圖。

具體實施方式

下面通過具體實施方式結合附圖對本發明作進一步詳細說明。

在對重疊頻分復用技術研究中，發明人發現傳輸功率的增長主要跟被復用信號(即調制窗函數)的頻譜有關，并非如理論上所設想的對復用信號頻譜的形狀、帶寬沒有任何要求。雖然現有技術中存在很多窗函數，理論上可自由采用各種窗函數對傳輸的正負符號序列進行調制，但由于矩形窗相較于其它窗函數在產生、設計和應用上更容易、成本更低，因此目前在進行信號調制時優先采用矩形窗，而矩形波的頻譜波形在兩側較陡峭，從而其在時間域上能量不集中，持續時間過長，因此復用波形系統性能很差，導致所需的傳輸功率和誤碼率都很高。

基于上述發現，在本發明實施例中，在應用重疊頻分復用技術時采用一種優于矩形波的窗函數對傳輸的正負符號序列進行調制。

請參考圖3，重疊頻分復用系統包括發射機1和接收機2。

發射機1包括重疊頻分復用調制裝置10和發射裝置20，其中，重疊頻分復用調制裝置10用于調制生成攜帶輸出信號序列的復調制包絡波形，發射裝置20用于將上述復調制包絡波形發射到接收機2。

請參考圖4，重疊頻分復用調制裝置10包括波形生成模塊11、移位模塊12、轉換模塊13、乘法模塊14、疊加模塊15和變換模塊16。

波形生成模塊11用于根據設計參數生成一個頻域內波形平滑的初始包絡波形。在一實施例中，設計參數至少包括初始包絡波形的帶寬寬度。

移位模塊12用于根據重疊復用次數將初始包絡波形在頻域上按預定的頻譜間隔進行移位，得到各子載波包絡波形。在一實施例中，頻譜間隔為子載波頻譜間隔△B，其中子載波頻譜間隔△B＝B/K，B為初始包絡波形的帶寬，K為重疊復用次數。在一實施例中，所述子載波頻譜間隔△B大于或等于系統采樣的倒數。

轉換模塊13用于將輸入的數字信號序列轉換成正負符號序列。在一實施例中，轉換模塊13將輸入的數字信號序列轉換成正負符號序列具體為：將輸入的數字信號序列中的0轉換為+A，數字信號序列中的1轉換為-A，以形成正負符號序列并輸出。例如，取A＝1，在一具體實施例中，轉換模塊13采用BPSK調制方式，將輸入的{0，1}比特序列經過調制轉換成{+1，-1}的符號序列。

乘法模塊14用于將上述正負符號序列中的符號與各自對應的子載波包絡波形相乘，得到各子載波的調制包絡波形。

疊加模塊15用于將上述各子載波的調制包絡波形在頻域上進行疊加，得到頻域上的復調制包絡波形。

變換模塊16用于將上述頻域上的復調制包絡波形變換到到時域上的復調制包絡波形。在一具體實施例中，變換模塊16可以采用傅氏反變換，將上述頻域上的復調制包絡波形變換成時域上的復調制包絡波形。

上述調制生成的復調制包絡波形攜帶有與轉換得到的正負符號序列對應的輸出信號序列，此輸出信號序列由各頻譜間隔的輸出信號組成，各頻譜間隔的輸出信號為各頻譜間隔內的調制包絡波形的運算值疊加后的結果，當調制包絡波形由正符號與子載波包絡波形相乘得到時，其運算值為+1，由負符號與子載波包絡波形相乘得到時，其運算值為-1。

返回參考圖3，接收機2包括接收裝置30和重疊頻分復用解調裝置40，其中，接收裝置30用于接收發射裝置20發送的上述復調制包絡波形，重疊頻分復用解調裝置40用于對接收的復調制包絡波形進行解調譯碼。

請參考圖5，接收裝置30包括符號同步模塊31和數字信號處理模塊32。

符號同步模塊31用于對接收的復調制包絡波形在時間域形成符號同步。

數字信號處理模塊32用于對各個符號時間區間的接收信號進行取樣、量化，使之變為接收符號序列。

請參考圖6，重疊頻分復用解調裝置40包括頻譜模塊41、頻率分段模塊42、卷積編碼模塊43和數據檢測模塊44。

頻譜模塊41用于將上述時間域上的接收符號序列進行變換以形成接收信號頻譜。在一具體實施例中，頻譜模塊41采用傅氏變換，將上述時間域上的接收符號序列變換成接收信號頻譜。

頻率分段模塊42用于將接收信號頻譜在頻域以子載波頻譜間隔△B進行分段得到接收信號分段頻譜。

卷積編碼模塊43用于對各子載波頻譜間隔△B內的接收信號分段頻譜進行卷積編碼，得到接收信號頻譜與發射機1中經輸入的數字信號序列轉換成的正負符號序列之間的一一對應關系。

數據檢測模塊44用于根據上述一一對應關系，檢測出上述正負符號序列。

請參考圖7，本申請還公開了一種重疊頻分復用調制方法，其包括以下步驟：

步驟S11、根據設計參數生成一個頻域內波形平滑的初始包絡波形。在一實施例中，設計參數至少包括初始包絡波形的帶寬寬度。

步驟S12、根據重疊復用次數將所述初始包絡波形在頻域上按預定的頻譜間 隔進行移位，得到各子載波包絡波形。在一實施例中，頻譜間隔為子載波頻譜間隔△B，其中子載波頻譜間隔△B＝B/K，B為初始包絡波形的帶寬，K為重疊復用次數。在一實施例中，所述子載波頻譜間隔△B大于或等于系統采樣的倒數。

步驟S13、將輸入的數字信號序列轉換成正負符號序列。在一實施例中，步驟S13將輸入的數字信號序列轉換成正負符號序列具體為：將輸入的數字信號序列中的0,1轉換為±A，A取值為非0任意數，以形成正負符號序列。例如，取A為1時，在一具體實施例中，步驟S13采用BPSK調制方式，將輸入的{0，1}比特序列經過調制轉換成{+1，-1}的符號序列。

步驟S14、將上述正負符號序列中的符號與各自對應的子載波包絡波形相乘，得到各子載波的調制包絡波形。

步驟S15、將上述各子載波的調制包絡波形在頻域上進行疊加，得到頻域上的復調制包絡波形。

步驟S16、將上述頻域上的復調制包絡波形變換到時域上的復調制包絡波形。在一具體實施例中，步驟S16可以采用傅氏反變換，將上述頻域上的復調制包絡波形變換成時域上的復調制包絡波形。

上述調制生成的復調制包絡波形攜帶有與轉換得到的正負符號序列對應的輸出信號序列，如圖8所示，此輸出信號序列可通過以下步驟確定：

步驟S17、當調制包絡波形由正符號與子載波包絡波形相乘得到時，令該調制包絡波形的運算值為+1，當調制包絡波形由負符號與子載波包絡波形相乘得到時，令該調制包絡波形的運算值為-1；

步驟S18、對于每個頻譜間隔，將位于該頻譜間隔內的調制包絡波形的運算值疊加，得出該頻譜間隔的輸出信號，從而形成輸出信號序列。

下面再以一個實際的例子對上述內容加以解釋說明。

不妨令輸入的數字信號序列轉換成的正負符號序列為X＝{X₀，X₁，…,X_N-1}，可以看到，正負符號序列的長度為N，N為正整數。

對該正負符號序列X＝{X₀，X₁，…,X_N-1}的重疊頻分復用調制過程如下：

在步驟S11中根據設計參數生成一個頻域內波形平滑的初始包絡波形H(f)。

在步驟S12中根據重疊復用次數將所述初始包絡波形在頻域上按預定的頻譜間隔進行移位，得到各子載波包絡波形。在一實施例中，具體地，將初始包絡波形H(f)分別頻移0到N-1個子載波頻譜間隔△B，得到N個子載波包絡波形，其中第i個子載波包絡波形為H(f-i*ΔB)，0≦i≦N-1；子載波頻譜間隔△B＝B/K，B為初始包絡波形H(f)的帶寬，K為重疊復用次數。

在步驟S14中將上述正負符號序列中的符號與各自對應的子載波包絡波形相乘，得到各子載波的調制包絡波形。在一實施例中，具體地，將上述正負符號序列的N個符號與各符號對應的子載波包絡波形相乘，得到N個經過子載波調制的調制包絡波形，其中第i個調制包絡波形為X_i*H(f-i*ΔB)，0≦i≦N-1。

在步驟S15中將上述各子載波的調制包絡波形在頻域上進行疊加，得到頻域上的復調制包絡波形

在步驟S16中將上述頻域上的復調制包絡波形S(f)進行變換，得到時域上的復調制包絡波形S(t)。

上述調制生成的復調制包絡波形S(f)和S(t)均攜帶有與正負符號序列X＝{X₀，X₁，…,X_N-1}對應的輸出信號序列S＝{S₀，S₁，…,S_N-1}。輸出信號序列S＝{S₀，S₁，…,S_N-1}可由圖8中的步驟S17與步驟S18進行確定。在一實施例中，具體地，請參考圖9，為K路波形復用的疊加原理示意圖，其呈四邊形形狀。其中每一行的項表示一個所要發送的符號X_i與對應的子載波包絡波形H(f-i*ΔB)相乘后形成的調制包絡波形X_i*H(f-i*ΔB)的K個采樣點，在同一列的項表示這些采樣點位于同一個頻譜間隔內，可進行疊加，得出該頻譜間隔的輸出信號，從而形成輸出信號序列。在本實施例中，系數A₀到A_K-1都令其為1。

實施例一

本實施例中，初始包絡波形為泰勒(Taylor)窗包絡波形，泰勒(Taylor)窗包絡波形在頻域內波形平滑。

下面以一個具體的例子來加以說明。

不妨以重疊復用次數K＝3，輸入的數字信號序列轉換成的正負符號序列X＝{-1，+1，+1，-1，+1，+1，+1，-1}為例，其中X₁＝-1，X₂＝+1，X₃＝+1，X₄＝-1，X₅＝+1，X₆＝+1，X₇＝+1，X₈＝+1，可以看到，正負符號序列X的長度N＝8。

在步驟S11中，根據設計參數生成一個泰勒(Taylor)窗包絡波形H(f)，在一實施例中，泰勒(Taylor)窗包絡波形H(f)的帶寬B＝63，如圖10所示，圖10(a)為當nbar＝4,sll＝-30時，泰勒(Taylor)窗包絡波形H(f)的頻域圖；圖10(b)為當nbar＝6,sll＝-50時，泰勒(Taylor)窗包絡波形H(f)的頻域圖；圖10(c)為當nbar＝8,sll＝-80時，泰勒(Taylor)窗包絡波形H(f)的頻域圖，其中在matlab中，泰勒(Taylor)窗包絡波形可用以下函數進行生成w＝taylorwin(n,nbar,sll)。從圖10中可以看到，隨著nbar的增加，泰勒(Taylor)窗包絡波形H(f)的波形起點越來越趨近于0，最高點的值越來越大，波形也越來越平滑；隨著sll的增加，頻域中旁瓣衰減越來越大。

在步驟S12中，根據重疊復用次數K將泰勒(Taylor)窗包絡波形H(f)在頻域上按預定的頻譜間隔進行移位，得到各子載波包絡波形。具體地，將泰勒(Taylor)窗包絡波形H(f)分別頻移0到7個子載波頻譜間隔△B，得到8個子載波包絡波形，其中第i個子載波包絡波形為H(f-i*ΔB)，0≦i≦7；子載波頻譜間隔△B＝B/K＝63/3＝21。

在步驟S14中，將正負符號序列X中的8個符號與各自對應的子載波包絡波形相乘，得到各子載波的調制包絡波形，其中第i個子載波包絡波形為X_i*H(f-i*ΔB)，0≦i≦7，各子載波包絡波形的頻域圖如圖11所示，其中，圖11(a)、(b)和(c)分別為由圖10(a)、(b)和(c)中的初始包絡波形調制得而到的調制包絡波形，在圖11中，波形1、2和3表示相乘后的各子載波包絡波形的頻域圖。

在步驟S15中，將上述各子載波的調制包絡波形在頻域上進行疊加，得到頻域上的復調制包絡波形如圖11所示，其中，圖11(a)、(b)和(c)還分別為由圖10(a)、(b)和(c)中的初始包絡波形調制得而到的復調制包絡波形，其中波形4為復調制包絡波形S(f)的頻域圖。

在步驟S16中，將上述頻域上的復調制包絡波形S(f)進行變換，得到時域上的復調制包絡波形S(t)，S(t)＝ifft(S(f))，ifft為傅里葉反變換函數。時域上的復調制包絡波形S(t)如圖12所示，其中，圖12(a)、(b)和(c)分別為由圖10(a)、(b)和(c)中的初始包絡波形調制得而到的復調制包絡波形的時域圖。可以看到，其在時間域上能量集中且持續時間短，其中圖12的橫坐標表示采樣點，縱坐標表示功率，單位為dB。最后將此時域上的復調制包絡波形S(t)發送出去。

此復調制頻譜信號S(f)和S(t)均攜帶有與正負符號序列X＝{-1，+1，+1，-1，+1，+1，+1，-1}對應的輸出信號序列S＝{S₀，S₁，…,S₇}。輸出信號序列是通過步驟S17和步驟S18進行計算得來的。在一實施例中，參照圖9中K路波形復用的疊加原理示意圖，將復用次數K，系數A₀到A₂以及符號X₁到X₇的值都代入其中，可得到圖13的3路波形復用疊加圖，從而計算出與正負符號序列X＝{-1，+1，+1，-1，+1，+1，+1，-1}對應的輸出信號序列S＝{-1，0，+1，+1，+1，+1，+3，+1}。

從圖10中可以看到，泰勒(Taylor)窗包絡波形H(f)當nbar＝4,sll＝-30時，其在頻域由0.4開始，最高點的值為1.55；當nbar＝8,sll＝-80時，其在頻域由0.01開始，最高點的值為2.38，隨著nbar越來越大，sll越來越小，泰勒(Taylor)窗包絡波形在頻域也越來越平滑，這導致由其頻域線性疊加后形 成的復調制包絡波形S(f)在頻域上的波形也越來越平滑，從圖11中可以清楚地看到這一點，頻域上波形平滑的復調制包絡波形S(f)轉換成時域上的復調制包絡波形S(t)后，復調制包絡波形S(t)在時域上能量越集中且持續時間越短，從圖12中可以清楚地看到這一點。因此，被調制后進行發送的復調制包絡波形，其在頻域上波形平滑，在時域上能量集中且持續時間短，使得本申請的重疊頻分復用調制方法、裝置及系統具有優好的性能，下面具體說明。

如圖14為矩形窗包絡波形的頻域圖，可以看到，其帶寬較寬，在頻域上由1開始處，頻譜不平滑，很陡峭，這導致由其作為初始包絡波形進行調制而形成的復調制包絡波形在頻域上也不平滑，從圖15中可以清楚地看到這一點，從而使得該復調制包絡波形在時域上能量分散且持續時間較長，從圖16中可以清楚地看到這一點。

因此，從圖中可以看出，相比由矩形窗包絡波形作為初始包絡波形調制而得到的復調制包絡波形，由泰勒(Taylor)窗包絡波形作為初始包絡波形調制而得到的復調制包絡波形，其頻域占用帶寬一樣，但時域上能量集中持續時間短，從而使得本申請的頻譜利用率得到了提高，同時，時域上能量集中持續時間短，又使得本申請的傳輸速率得到了提高，另外，由泰勒(Taylor)窗包絡波形作為初始包絡波形調制而得到的復調制包絡波形在頻域很平滑，使得本申請在對頻域上的波形進行波形切割的精度高，降低了誤碼率。

由發射機1發送的上述由泰勒(Taylor)窗包絡波形作為初始包絡波形調制而得到時域上的復調制包絡波形S(t)，可由接收機2進行接收和解調。具體地，先對接收到的復調制包絡波形在時間域形成符號同步；接著，對各個符號時間區間的接收信號進行取樣、量化，使之變為接收符號序列；接著，將上述時間域上的接收符號序列進行變換以形成接收信號頻譜；接著，將接收信號頻譜在頻域以子載波頻譜間隔△B進行分段得到接收信號分段頻譜。經過上述處理后，頻譜波形切割得到的接收符號序列為S＝{-1，0，+1，+1，+1，+1，+3，+1}，即是復調制頻譜信號S(f)和S(t)攜帶的與正負符號序列X＝{-1，+1，+1，-1，+1，+1，+1，-1}對應的輸出信號序列S＝{-1，0，+1，+1，+1，+1，+3，+1}。最后就是根據一定的譯碼算法對切割后的頻譜波形進行譯碼。在一實施例中，具體地，是根據圖17中的輸入-輸出關系圖和圖18中的節點狀態轉移圖，進行符號之間的前后比較，得到節點轉移路徑，從而進行譯碼。具體地，請返回參照圖17，向上的樹枝(路徑)為表示輸入+1，向下的樹枝表示輸入-1，仔細觀察可發現，在第三枝以后該樹圖就變成重復的了，因為凡是從標記為a的節點輻射出的樹枝都有同樣的輸出，該結論對節點b、c、d也同樣適用。它們不外 乎是如下幾種可能，如圖18所示，從圖中可以看出從節點a只能轉移到(經輸入+1)節點a及(經輸入-1)節點b，同時b只能到(輸入+1)c及(輸入-1)d，c只能到(輸入+1)a及(輸入-1)b，d只能到(輸入+1)c及(輸入-1)d。產生這種現象的原因很簡單，因為只有相鄰K個符號才會形成相互“干擾”。所以當頻率域第K位數據輸入到信道時，最早來的第1位數據已經移出最右邊的一個頻率間隔了。因此信道的輸出除了取決于現頻率數據的輸入，還決定于前K-1個頻率數據的輸入。本實施例中，節點狀態轉移路徑為圖17中的加黑粗線，節點轉移路徑為-1(接收符號序列為S的第一個符號為-1)->b->c->a->b->c->a->a->b，根據此轉移關系即求出輸入的符號序列為{-1，+1，+1，-1，+1，+1，+1，-1}，可以看到，譯碼后得出的符號序列即為正負符號序列X。

實施例二

相比實施例一，本實施例中，初始包絡波形為頻域內波形平滑的泰勒(Taylor)窗演變窗函數的包絡波形，比如泰勒(Taylor)窗脈沖成型連乘函數、各階導數、各階導數之和等一系列關于泰勒(Taylor)窗脈沖成型的函數形式的包絡波形。

下面以初始包絡波形為泰勒(Taylor)窗一階導包絡波形為例，進行詳細說明。

仍以實施例一中重疊復用次數K＝3，正負符號序列X＝{-1，+1，+1，-1，+1，+1，+1，-1}為例。

在步驟S11中，根據設計參數生成一個泰勒(Taylor)窗一階導包絡波形H(f)，在一實施例中，泰勒(Taylor)窗一階導包絡波形H(f)的帶寬B＝63，如圖19所示，為泰勒(Taylor)窗一階導包絡波形H(f)的三種頻域圖，其中圖19(a)為當nbar＝4,sll＝-30時，泰勒(Taylor)窗一階導包絡波形H(f)的頻域圖；圖19(b)為當nbar＝6,sll＝-50時，泰勒(Taylor)窗一階導包絡波形H(f)的頻域圖；圖19(c)為當nbar＝8,sll＝-80時，泰勒(Taylor)窗一階導包絡波形H(f)的頻域圖。

在步驟S12中，根據重疊復用次數K將泰勒(Taylor)窗一階導包絡波形H(f)在頻域上按預定的頻譜間隔進行移位，得到各子載波包絡波形。具體地，將泰勒(Taylor)窗一階導包絡波形H(f)分別頻移0到7個子載波頻譜間隔△B，得到8個子載波包絡波形，其中第i個子載波包絡波形為H(f-i*ΔB)，0≦i≦7；子載波頻譜間隔△B＝B/K＝63/3＝21。

在步驟S14中，將正負符號序列X中的8個符號與各自對應的子載波包絡波形相乘，得到各子載波的調制包絡波形，其中第i個子載波包絡波形為X_i*H(f-i*ΔB)，0≦i≦7，各子載波包絡波形的頻域圖如圖20所示，其中，圖20(a)、(b)和(c)分別為由圖19(a)、(b)和(c)中的初始包絡波形調制得而到的調制包絡波形，在圖20中，波形1、2和3表示相乘后的各子載波包絡波形的頻域圖。

在步驟S15中，將上述各子載波的調制包絡波形在頻域上進行疊加，得到頻域上的復調制包絡波形如圖20所示，其中，圖20(a)、(b)和(c)中的波形4還分別為由圖19(a)、(b)和(c)中的初始包絡波形調制得而到的復調制包絡波形。

在步驟S16中，將上述頻域上的復調制包絡波形S(f)進行變換，得到時域上的復調制包絡波形S(t)，S(t)＝ifft(S(f))，如圖21所示，圖21(a)、(b)和(c)分別為由圖19(a)、(b)和(c)中的初始包絡波形調制得而到的復調制包絡波形的時域圖，可以看到，其在時間域上能量集中且持續時間短，其中圖12的橫坐標表示采樣點，縱坐標表示功率，單位為dB。最后將此時域上的復調制包絡波形S(t)發送出去。

從圖19可以看到，泰勒(Taylor)窗一階導包絡波形H(f)頻譜平滑，這導致由其頻域線性疊加后形成的復調制包絡波形S(f)在頻域上的波形也很平滑，這點從圖20中可以清楚看到。頻域上波形平滑的復調制包絡波形S(f)轉換成時域上的復調制包絡波形S(t)，復調制包絡波形S(t)在時域上能量集中且持續時間短，這點由圖21可以清楚看出，且隨著nbar的增加,sll的減少，復調制包絡波形在頻域上越平滑，在時域上能量越集中持續時間越短。因此，被調制后進行發送的復調制包絡波形，其在頻域上波形平滑，在時域上能量集中且持續時間短，使得本申請的重疊頻分復用調制方法、裝置及系統具有優好的性能。相比選用矩形窗包絡波形作為初始包絡波形的系統，本申請選用頻域上波形平滑的泰勒(Taylor)窗一階導包絡波形作為初始包絡波形，基于與實施例一相似的理由，使得本申請頻譜利用率高，信號傳輸速率也高，并且只需要較低的傳輸功率，被解調時具有較低的誤碼率。

本申請各實施例，針對現在有重疊頻分復用波形(即調制窗函數，也就是初始包絡波形)進行分析，成功地找到了一種適用于重疊頻分復用調制方法、裝置和系統的頻域波形函數，此頻域波形函數要求頻域上波形平滑，從而其轉換到時域后能量集中且持續時間短，使用此頻域波形函數作為初始包絡波形后， 調制得到的復調制包絡波形在頻域同樣波形平滑，在時域上能量集中且持續時間短，從而使得本申請的重疊頻分復用調制方法、裝置和系統在重疊復用次數K一定時，其相對于矩形窗函數作為初始包絡波形的系統，頻譜利用率和傳輸速度提到了大幅提高，傳輸功率和誤碼率得到了大幅降低。

以上應用了具體個例對本發明進行闡述，只是用于幫助理解本發明，并不用以限制本發明。對于本發明所屬技術領域的技術人員，依據本發明的思想，還可以做出若干簡單推演、變形或替換。