修復多節點失效的MDS陣列碼編碼以及解碼方法與流程

【
技術領域：
】本發明涉及數據處理領域，尤其涉及一種修復多節點失效的mds陣列碼編碼以及解碼方法。
背景技術：
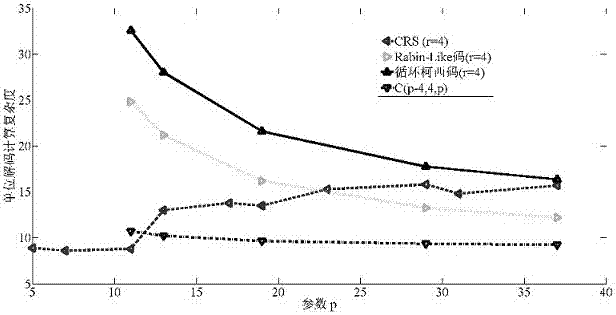
：隨著計算機網絡應用的迅速發展，網絡信息數據量變得越來越大，海量信息存儲變得尤為重要，持續增長的數據存儲壓力推動著整個存儲市場的快速發展。分布式存儲以其高性價比、低初期投資、按需付費等優越的特點日益成為當今大數據存儲的主流技術。當前，分布式存儲系統的存儲節點失效已經成為一種常態。當系統所部署的存儲節點變得不可靠時，必須引入冗余來提高節點失效時的可靠性。引入冗余最簡單的方法就是對原始數據直接備份，直接備份雖然簡單但是其存儲效率和系統可靠性不高，而通過編碼引入冗余的方法可以提高其存儲效率，增強系統的可靠性。因此分布式存儲的高概率可用性、可靠性以及安全性等均是分布式存儲系統的關鍵技術問題。在目前的存儲系統中，編碼方法一般采用mds碼，mds碼可以達到存儲空間效率的最優化，一個(n,k)mds碼需要將一個原始數據文件分成k個大小相等的數據塊，通過線性編碼生成n個互不相關的編碼塊，并由n個節點存儲n個編碼塊。若n個編碼塊中包含原始的k個數據塊，其它n-k個編碼塊稱為冗余塊，包含k個數據塊的mds碼稱為系統mds碼。mds碼滿足mds屬性：即從n個編碼塊中取任意k個即可解碼出原始的k個數據塊。這種編碼技術在提供有效的網絡存儲編碼中占有重要的地位，特別適合應用于存儲大的文件以及檔案數據備份。在分布式存儲系統中，把數據按某種方式編碼，并把編碼結果存儲在n個存儲節點中，這一過程稱為編碼過程。數據接收者只需連接并下載n個存儲節點中的任意k個存儲節點的數據即可恢復出原始數據，這一過程稱為數據重建過程或解碼過程。不同的mds碼有不同的編碼、解碼計算復雜度。復雜度越高，計算量越大，計算時所消耗的時間就越長。設計出一種好的mds碼，能夠降低計算量，縮短工作時間，減少資源的消耗，節省系統運行時需要的成本，使得運算和存儲更加靈活。mds陣列碼是mds碼的一種，其特征是編解碼過程中僅僅用到簡單的二進制異或操作，因此可以很容易且高效的在系統中實現。本發明即是一種能容納任意n-k個編碼塊的丟失，編碼、解碼計算復雜度低的二進制系統mds陣列碼。evenodd碼，引自論文[m.blaum,j.brady,j.bruck,andj.menon,“evenodd:anefficientschemefortoleratingdoublediskfailuresinraidarchitectures,”ieeetransactionsoncomputers,vol.44,no.2,pp.192–202,1995]。evenodd碼是能容納2個編碼塊丟失的mds陣列碼。在evenodd碼中，其要求數據塊個數必須為質數，冗余塊個數為2。evenodd碼的編碼過程只需要簡單的二進制異或運算，并且兩個檢驗塊的每個冗余比特均是通過斜率為0和1的直線經過的信息比特異或結果。但是，evenodd碼存在著不可拓展性的缺陷：evenodd碼只有兩個檢驗塊，因此最多只能恢復兩個存儲節點失效的情況，不易于拓展。文獻[m.blaum,j.bruck,anda.vardy.mdsarraycodeswithindependentparitysymbols.inieeetransactionsoninformationtheory,vol.42,no.2,pp.529-542,1996]給出了evenodd碼的擴展，但是滿足mds屬性的條件非常苛刻，且滿足mds屬性的冗余塊個數(n-k)最大為8。crs碼，全稱是cauchyreed-solomon碼，引自論文[plank,j.s.,xu,l.optimizingcauchyreed-solomoncodesforfault-tolerantnetworkstorageapplications.inieeeinternationalsymposiumonnetworkcomputingandapplications,pp.173–180,2006]。它是基于有限域和cauchy矩陣構造的mds系統陣列碼，可以容納任意的n-k個編碼塊的丟失。在編碼、解碼過程中，它把一個有限域乘法運算轉換為多個二進制異或運算。但是，crs碼依然存在著編碼、解碼計算復雜度高的缺點：crs碼在編解碼過程中，把有限域乘法運算轉換為多個二進制異或運算，因為二進制異或運算的個數就反應了其編解碼計算復雜度，然而其對應的二進制異或運算的個數在編解碼過程中是不可控的、很高的。對于一般的參數k和n，如何設計其編解碼計算方法，降低二進制異或個數，即編解碼計算復雜度，是crs碼急需解決的一大缺陷。技術實現要素：為了解決現有技術中的問題，本發明提供了一種修復多節點失效的mds陣列碼編碼以及解碼方法，解決現有技術中編解碼計算復雜度高的問題。本發明是通過以下技術方案實現的：設計、制造了一種修復多節點失效的mds陣列碼編碼，其組成部分為c(k，r，p)碼，通過構建一個(p-1)×(k+r)的矩陣來存儲原始信息數據塊和冗余塊，其中p為質數，且p大于k和r，k和r小于為小于p大于0的任意整數；k列稱為信息列，其對應為k個數據塊；r列為冗余列，其對應為r個冗余塊，c(k，r，p)碼中的加法和減法運算均為異或運算。作為本發明的進一步改進：c(k，r，p)碼的構造過程為：給定k(p-1)個信息比特，計算并添加k個校驗比特，得到k個數據多項式，通過計算出編碼多項式，存儲多項式的次數為從0到p-2的多項式的系數。作為本發明的進一步改進：存儲在第j信息列的p-1個信息比特和其校驗比特表示的第一數據多項式為sj(x)＝s0,j+s1,jx+…+sp-2,jxp-2+sp-1,jxp-1，其中，si,j表示陣列碼c(k,r,p)的第j信息列的第i個比特；第三編碼多項式為作為本發明的進一步改進：c(k，r，p)碼中的除法按以下方式進行：為每個數據多項式計算一個除法運算，然后把相應的數據多項式除法運算的結果相加。作為本發明的進一步改進：c(k，r，p)碼為二進制柯西陣列碼，其生成矩陣為g＝[ic]，其中矩陣i表示k×k的單位陣，矩陣c為的k×r柯西矩陣，本發明同時提供了一種修復多節點失效的mds陣列碼編碼的解碼方法，包括如下步驟：當陣列碼c(k,r,p)中有ρ≤r個列丟失時，設γ個信息列a1,a2,...,aγ和δ個冗余列b1,b2,...,bδ丟失，其中1≤a1＜a2＜...＜aγ≤k，1≤b1＜b2＜...＜bγ≤r，k≥γ≥0，r≥δ≥0且γ+δ＝ρ≤r，把存活的沒有丟失的信息列表示為m＝{1,2,...,k}\{a1,a2,...,aγ}，把沒有丟失的冗余列表示為p＝{1,2,...,r}\{b1,b2,...,bδ}，首先下載存活的沒有丟失的k-γ個信息列i1,i2,...,ik-γ∈m，和γ個冗余列l1,l2,...,lγ∈p，恢復出丟失的γ個信息列，然后把丟失冗余列的編碼向量與k個數據多項式相乘計算出丟失的冗余多項式。作為本發明的進一步改進：為信息列iτ添加一個校驗比特并形成數據多項式其中τ＝1,2,...,k-γ；為冗余列lh添加比特零并形成編碼多項式其中，h＝1,2,...,γ；分別為γ個編碼多項式減去k-γ個數據多項式所得到的多項式為，通過求解線性方程組解出丟失的γ個數據多項式，其中線性方程組為；然后獲得γ個丟失的信息列。作為本發明的進一步改進：丟失的δ個冗余列通過相應的編碼向量與k個信息多項式相乘得到。本發明的有益效果是：能修復任意n-k個節點失效且編解碼計算復雜度較低的新cauchy陣列碼，提高了系統的容錯性。通過二進制異或運算實現了新cauchy陣列碼的編解碼，與crs碼相比，編解碼過程的計算復雜度更低。【附圖說明】圖1為本發明陣列碼c(p-4,4,p)、循環柯西碼和crs碼在r＝4時的單位編碼計算復雜度示意圖；圖2為本發明陣列碼c(p-4,4,p)和、rabin-like碼、循環柯西碼和crs碼在r＝4時的單位解碼計算復雜度示意圖；圖3為本發明陣列碼c(p-5,5,p)、循環柯西碼和crs碼在r＝5時的單位解碼計算復雜度示意圖。【具體實施方式】下面結合附圖說明及具體實施方式對本發明進一步說明。縮略語和關鍵術語定義mdsmaximumdistanceseparable最大距離可分離rdprow-diagonalparity行對角線校驗一種修復多節點失效的mds陣列碼編碼，其組成部分為c(k，r，p)碼，通過構建一個(p-1)×(k+r)的矩陣來存儲原始信息數據塊和冗余塊，其中p為質數，且p大于k和r，k和r小于為小于p大于0的任意整數；k列稱為信息列，其對應為k個數據塊；r列為冗余列，其對應為r個冗余塊，c(k，r，p)碼中的加法和減法運算均為異或運算。c(k，r，p)碼的構造過程為：給定k(p-1)個信息比特，計算并添加k個校驗比特，得到k個數據多項式，通過計算出編碼多項式，存儲多項式的次數為從0到p-2的多項式的系數。存儲在第j信息列的p-1個信息比特和其校驗比特表示的第一數據多項式為sj(x)＝s0,j+s1,jx+…+sp-2,jxp-2+sp-1,jxp-1，其中，si,j表示陣列碼c(k,r,p)的第j信息列的第i個比特；第三編碼多項式為c(k，r，p)碼中的除法按以下方式進行：為每個數據多項式計算一個除法運算，然后把相應的數據多項式除法運算的結果相加。c(k，r，p)碼為二進制柯西陣列碼，其生成矩陣為g＝[ic]，其中矩陣i表示k×k的單位陣，矩陣c為的k×r柯西矩陣，本發明同時提供了一種修復多節點失效的mds陣列碼編碼的解碼方法，包括如下步驟：當陣列碼c(k,r,p)中有ρ≤r個列丟失時，設γ個信息列a1,a2,...,aγ和δ個冗余列b1,b2,...,bδ丟失，其中1≤a1＜a2＜...＜aγ≤k，1≤b1＜b2＜...＜bγ≤r，k≥γ≥0，r≥δ≥0且γ+δ＝ρ≤r，把存活的沒有丟失的信息列表示為m＝{1,2,...,k}\{a1,a2,...,aγ}，把沒有丟失的冗余列表示為p＝{1,2,...,r}\{b1,b2,...,bδ}，首先下載存活的沒有丟失的k-γ個信息列i1,i2,...,ik-γ∈m，和γ個冗余列l1,l2,...,lγ∈p，恢復出丟失的γ個信息列，然后把丟失冗余列的編碼向量與k個數據多項式相乘計算出丟失的冗余多項式。為信息列iτ添加一個校驗比特并形成數據多項式其中τ＝1,2,...,k-γ；為冗余列lh添加比特零并形成編碼多項式其中，h＝1,2,...,γ；分別為γ個編碼多項式減去k-γ個數據多項式所得到的多項式為通過求解線性方程組解出丟失的γ個數據多項式，其中線性方程組為然后獲得γ個丟失的信息列。丟失的δ個冗余列通過相應的編碼向量與k個信息多項式相乘得到。本發明中，這種新的基于二進制多項式環和cauchy矩陣構造的mds陣列碼針對現有的mds碼一般容納存儲節點失效個數少、編解碼計算復雜度高等問題，提出來了一種能修復任意n-k個節點失效且編解碼計算復雜度較低的新cauchy陣列碼，提高了系統的容錯性。通過二進制異或運算實現了新cauchy陣列碼的編解碼，并且與crs碼相比，編解碼過程的計算復雜度更低。簡稱這種新cauchy陣列碼為c(k,r,p)碼，本文的所有的加法運算和減法運算均指二進制異或運算，其中r＝n-k。c(k,r,p)碼通過構建一個(p-1)×(k+r)的矩陣來存儲原始信息數據塊和冗余塊，其中p為質數，且p大于k和r，k和r小于為小于p大于0的任意整數。c(k,r,p)碼的前k列稱為信息列，對應為k個數據塊，后r列為冗余列，對應為r個冗余塊。在一實施例中，c(k,r,p)碼的構造過程如下：令i＝0,1,...,p-2，j＝1,2,...,k，用si,j表示陣列碼c(k,r,p)的第j信息列的第i個比特。令i＝0,1,...,p-2，l＝1,2,...,r，用ci,j表示陣列碼c(k,r,p)的第l冗余列的第i個比特。對于存儲在第j信息列的p-1個信息比特s0,j,s1,j,…,sp-2,j，定義校驗比特sp-1,j為sp-1,j＝s0,j+s1,j+…+sp-2,j。令j＝1,2,...,k，把存儲在第j信息列的p-1個信息比特和其校驗比特表示為數據多項式sj(x)＝s0,j+s1,jx+…+sp-2,jxp-2+sp-1,jxp-1。(1)同樣的，令l＝1,2,...,r，定義冗余列l的校驗比特cp-1,l為cp-1,l＝c0,l+c1,l+…+cp-2,l，并把存儲在第l冗余列的p-1個冗余比特和其校驗比特表示為編碼多項式cl(x)＝c0,l+c1,lx+…+cp-2,lxp-2+cp-1,lxp-1。(2)因此，現在有多項式環f2[x]/(1+xp)中的k個數據多項式和r個編碼多項式。而r個編碼多項式是由以下等式計算而得注意，以上計算均是多項式環f2[x]/(1+xp)中的運算。因此，陣列碼c(k,r,p)的生成矩陣為g＝[ic]，其中矩陣i表示k×k的單位陣，矩陣c為的k×r柯西矩陣二進制柯西陣列碼c(k,r,p)的編碼過程可以描述如下。給定k(p-1)個信息比特，計算并添加k個校驗比特，得到k個如式(1)所示的數據多項式。通過計算出式(3)所示的編碼多項式，忽略這些多項式中次數為p-1的項，然后存儲多項式的次數為從0到p-2的多項式的系數。在陣列碼c(k,r,p)的編碼過程中，需要在多項式環f2[x]/(1+xp)中計算很多形如的除法運算，其中多項式s(x)有偶數個項，b是小于素數p的一個正整數。在以下引理中給出了如何有效的計算這種除法運算。引理1.在多項式環f2[x]/(1+xp)中，多項式s(x)＝s0+s1x+…+sp-1xp-1有偶數個項，給定正整數b和等式其中b是小于素數p的一個正整數。則可以通過以下等式計算出多項式c(x)＝c0+c1x+…+cp-1xp-1的系數。證明：通過把等式s(x)＝c(x)(1+xb)展開有，選擇多項式c(x)的一個系數為0，然后多項式c(x)的其它系數可以通過以上等式迭代的計算出。具體的講，令系數cp-1等于0，然后可以計算出cp-b-1＝sp-1和cb-1＝sb-1。多項式c(x)的其它系數均可以通過一個異或運算迭代的計算出。證畢。由引理1的證明過程知，在計算多項式c(x)的系數過程中需要p-3個異或。以參數k＝2，r＝2，p＝5為例，介紹柯西陣列碼c(2,2,5)的編碼過程。在這個例子中，有兩個數據多項式，如式(5)和式(6)所示。s1(x)＝s0,1+s1,1x+s2,1x2+s3,1x3+(s0,1+s1,1+s2,1+s3,1)x4式(5)s2(x)＝s0,2+s1,2x+s2,2x2+s3,2x3+(s0,2+s1,2+s2,2+s3,2)x4式(6)兩個編碼多項式c1(x)和c2(x)由以下式(7)所示的等式計算而得。根據引理1，在以上計算編碼多項式的過程中，每個除法運算均涉及2個異或運算。表1列出了該例子的信息列比特和冗余列比特。在計算二進制柯西陣列碼的編碼多項式中，首先需要為每個數據多項式計算一個除法運算，然后把相應的數據多項式除法運算的結果相加。表1陣列碼c(2，2，5)的信息列和冗余列信息列1信息列2冗余列1冗余列2s0，1s0，2(s0，1+s1，1+s3，1)+(s0，2+s2，2)(s0，1+s1，1+s3，1)+(s0，2+s3，2)s1，1s1，2s1，1+(s0，2+s1，2+s2，2+s3，2)s1，1+s2，2s2，1s2，2(s0，1+s1，1+s2，1+s3，1)+s2，2(s0，1+s1，1+s2，1+s3，1)+s0，2s3，1s3，2(s1，1+s3，1)+(s0，2+s2，2+s3，2)(s1，1+s3，1)+(s0，2+s1，2+s3，2)在又一實施例中，陣列碼c(k，r，p)的解碼過程如下：當二進制柯西陣列碼的一些數據列丟失時，想要從其他存活的數據列中下載數據并解碼出丟失的數據。稱這一過程為解碼過程。本節給出陣列碼c(k，r，p)的一種快速解碼方法，這種方法是基于柯西矩陣的lu分解。該解碼方法適用于任意數據列的丟失。首先來介紹柯西矩陣的lu分解。給定2k個互不相等的變量x1，x2，...，xk，y1，y2，...，yk，柯西方陣被定義為如式(8)所示。文獻[t.boros，t.kailathandv.olshevsky.afastparallelbjorck-pereyra-typealgorithmforsolvingcauchylinearequations.elsevierlinearalgebraandltsapplications，vol.1999，302(1)：265-293.]中給出了柯西方陣的逆矩陣并提出了柯西矩陣逆矩陣的lu分解，主要結論如下。定理2.柯西方陣c(x1：k，y1：k)的逆矩陣可以被分解為式(9)所示。其中式(10)和式(11)滿足。其中i＝1,2,...,k-1，和式(12)滿足。dk＝diag{(x1-y1)(x2-y2)…(xk-yk)}式(12)舉例說明，當k＝2時，柯西逆矩陣c(x1:2,y1:2)-1可以分解為式(13)所示。基于定理2的結論，提出了一種快速求解柯西矩陣形式的線性方程組的方法。給定一個k×k柯西矩陣形式的線性方程組c(x1:k,y1:k)z＝b，其中z＝(z1,z2,...,zk)t和b＝(b1,b2,...,bk)t均是長度為k的列向量。當給定向量b＝(b1,b2,...,bk)t和矩陣c(x1:k,y1:k)的值時，可以求解出向量z＝(z1,z2,...,zk)t的值，為式(14)所示。算法的偽代碼請見算法1。在算法1中，需要處理三種運算：(i)多項式bl和xi的乘積，(ii)除法運算bl/(xj-yj-i)，(iii)多項式的加法運算bi+bj。可以統計算法1中共有5k(k-1)次第一種類型乘法運算，k(k-1)次第二種類型除法運算和k+3k(k-1)次第三種類型加法運算。對應到陣列碼c(k,r,p)的解碼過程中，算法1中的xi和yi均被x的冪所代替，而變量bl和則被多項式環f2[x]/(1+xp)中的一個多項式代替。算法1中所有的類型二除法運算均可以通過引理1給出的方法計算出，且一個除法運算涉及p-3次異或運算。對于第一種類型乘法運算，在多項式環f2[x]/(1+xp)中，一個多項式乘以xi就是這個多項式的循環移位i位，因此沒有涉及異或運算。在多項式環f2[x]/(1+xp)中，兩個多項式相加會用到p次異或運算。在算法1中，步驟5到7是計算矩陣的右矩陣和列向量b的乘積，共有3(k-i)個多項式加法運算，其計算復雜度最多為3p(k-i)次異或。步驟8到10則是計算矩陣的左矩陣和列向量b的乘積，其計算復雜度最多為3k(k-1)(p-3)/2次異或。因此，步驟5到10，計算矩陣和列向量b的乘積的計算復雜度最多為3pk(k-1)/2+3k(k-1)(p-3)/2次異或。步驟12到14是計算對角矩陣dk和以上步驟得到的多項式向量的乘積，其計算復雜度最多為p+(k-1)(p-2)次異或。步驟16到18是計算矩陣的右矩陣和以上步驟得到的多項式向量的乘積，其計算復雜度最多為(k-3)k(k-1)/2次異或。步驟19到26則是計算矩陣的左矩陣和以上步驟得到的多項式向量的乘積，其計算復雜度最多為k(k-1)(3p-4)/2次異或。所以，在多項式環f2[x]/(1+xp)中，算法1的計算復雜度最多為式(15)所示。考慮上文給出的例子，兩個編碼多項式是通過以下等式計算出式(16)所示等式。假設兩個數據多項式分別為s1(x)＝1+x和s2(x)＝x+x3。那么，可以得出其兩個編碼多項式分別為c1(x)＝x和c2(x)＝x+x2+x3。根據定理1，這個2×2的柯西矩陣可以分解為式(17)所示。可以驗證兩個數據多項式可以由兩個編碼多項式通過以下等式計算出式(18)。在求解兩個編碼多項式的過程中，有32個異或運算。當陣列碼c(k,r,p)中有ρ≤r個列丟失時，接下來描述陣列碼的解碼過程。假設γ個信息列a1,a2,...,aγ和δ個冗余列b1,b2,...,bδ丟失，其中1≤a1＜a2＜...＜aγ≤k，1≤b1＜b2＜...＜bγ≤r，k≥γ≥0，r≥δ≥0且γ+δ＝ρ≤r。把存活的沒有丟失的信息列表示為式(19)。m＝{1,2,...,k}\{a1,a2,...,aγ}式(19)把沒有丟失的冗余列表示為式(20)。p＝{1,2,...,r}\{b1,b2,...,bδ}式(20)首先下載存活的沒有丟失的k-γ個信息列i1,i2,...,ik-γ∈m，和γ個冗余列l1,l2,...,lγ∈p，恢復出丟失的γ個信息列，然后把丟失冗余列的編碼向量與k個數據多項式相乘計算出丟失的冗余多項式。下面詳細的介紹其解碼過程。對于τ＝1,2,...,k-γ，首先為信息列iτ添加一個校驗比特并形成數據多項式如式(21)。對于h＝1,2,...,γ，為冗余列lh添加比特零并形成編碼多項式如式(22)令式(23)分別為γ個編碼多項式減去k-γ個數據多項式所得到的多項式，則有式(24)。其中h＝1,2,...,γ。然后，可以通過求解以下線性方程組解出丟失的γ個數據多項式。如式(25)所示。通過調用算法1，可以得到γ個丟失的信息列。然后，丟失的δ個冗余列可以通過相應的編碼向量與k個信息多項式相乘得到。下面來分析編解碼的復雜度。下面統計下二進制柯西陣列碼的解碼復雜度。為k-γ個信息列添加校驗比特并形成數據多項式用到了(k-γ)(p-2)次異或運算。計算式子(22)所表示的γ個多項式需要γ((k-γ)(p-3)+(k-γ)(p-1))＝γ(k-γ)(2p-4)次異或運算。在求解γ×γ柯西形式的線性方程組時用到了4γ2p-3γp-5γ2+3γ+2次異或運算。在恢復δ個冗余列時需要δ(k(p-3)+(k-1)(p-1))次異或運算。因此，解碼出γ個信息列和δ個冗余列的解碼計算復雜度dγ，δ，為式(26)。次異或運算。當沒有冗余列丟失，僅僅有信息列丟失時，解碼復雜度為式(27)所示次異或運算。dγ＝(k-γ)(p-2)+γ(k-γ)(2p-4)+4γ2p-3γp-5γ2+3γ+2式(27)。為方便比較，定義單位編碼復雜度為編碼過程中涉及到的異或運算的個數除以信息比特的個數，單位解碼復雜度為解碼過程中涉及到的異或運算的個數除以信息比特的個數。相比于之前的編碼方案，比如evenodd碼，陣列碼c(k,r,p)的編解碼復雜度幾乎不變，但卻能大大提升系統的容錯能力，最多能修復任意r個節點失效；相比于crs碼，陣列碼c(k,r,p)在同樣能恢復多個節點失效的同時，編解碼復雜度均很低。其次，c(k,r,p)碼對原始信息數據塊的數量不固定，取值更加靈活。而且，c(k,r,p)碼的構造過程和重建過程均只涉及異或運算，所以計算復雜度很低、計算開銷很小，很大程度上降低了系統計算時延，節省時間和資源，能減少成本的消耗，適合實際的存儲系統；c(k,r,p)碼可以滿足mds屬性，在節省存儲空間的同時，又讓系統能夠容納多個結點故障，增加了數據的容錯性和穩定性。編碼計算復雜度：在陣列碼c(k,r,p)中，有k個信息列，r個冗余列。首先，為每個信息列計算一個校驗比特形成數據多項式，需要k(p-2)次異或運算。然后，根據編碼計算公式計算出r個編碼多項式。在計算每個編碼多項式的過程中，需要計算k個除法運算，根據引理8知需要個k(p-3)異或運算。另外，根據引理1的結論，除法運算所得多項式的次數為p-1的系數為0。因此，在計算每個編碼多項式的過程中的k-1個加法運算，需要(k-1)(p-1)次異或運算。所以，計算一個編碼多項式需要的異或個數e1為式(28)所示。e1＝k(p-3)+(k-1)(p-1)式(28)計算r個冗余列需要的計算量er，為式(29)所示。er＝k(p-2)+r(2kp-4k-p+1)式(29)二進制柯西陣列碼c(k,r,p)的單位編碼計算復雜度nec(k,r,p)，為式(30)。當給定冗余列的個數r時，循環柯西(circulantcauchy)陣列碼[c.schindelhauerandc.ortolf.maximumdistanceseparablecodesbasedoncirculantcauchymatrices.structuralinformationandcommunicationcomplexity.springer,2013,3(1):334-345.]的單位編碼計算復雜度為式(31)所示。為了公平的比較柯西陣列碼的編碼復雜度，令參數k等于p-r，因此有陣列碼c(k,r,p)的單位編碼計算復雜度為式(32)所示。當r＝4時，對陣列碼c(p-4,4,p)，令k＝p-4。當p取值范圍從11到47時，陣列碼c(p-4,4,p)、循環柯西陣列碼和crs碼的單位編碼計算復雜度如圖1。對于crs碼，令k＝p-4。在圖1中，crs碼的數值均是1000次運行數據的平均值。圖1的結果表明陣列碼c(p-4,4,p)的單位編碼計算復雜度是三種陣列碼中最低的，而crs碼的計算復雜度是三種陣列碼中最大的。解碼計算復雜度：同樣的，令k＝p-r，陣列碼c(p-r,r,p)的單位解碼計算復雜度ndc(p-r,r,p)，為式(33)所示。當r＝4時，rabin-like碼[g.l.feng,r.h.deng,f.bao,etal.newefficientmdsarraycodesforraid.partii.rabin-likecodesfortoleratingmultiple(≥4)diskfailures.ieeetransactionsoncomputers,2006,54(12):1473-1483]的解碼計算復雜度為p(9k+95)異或運算，而當r大于4時，其解碼計算復雜度會很大且作者并沒有給出精確地異或個數。當循環柯西陣列碼中有r個信息列丟失時，其單位解碼計算復雜度ndcc，為式(34)所示。當r＝4時，且當參數p取值范圍從11到37時，陣列碼c(p-4,4,p)、rabin-like碼、柯西循環碼和crs碼的單位解碼計算復雜度如圖2。圖2的結果表明，循環柯西碼、rabin-like碼和陣列碼c(p-4,4,p)均是隨著參數p的增加而減少，而crs碼則是隨著參數p的增加而增加。這是因為crs碼的解碼優化算法對參數值小時性能較好，而當參數值較大時，其優化效果不佳。因此，當參數較大時，crs碼的解碼計算復雜度是最大的，而當參數較小時，crs碼的解碼計算復雜度相對較低。在陣列碼c(p-4,4,p)、rabin-like碼和柯西循環碼中，陣列碼c(p-4,4,p)的解碼計算復雜度是最低的，無論是當參數p取值小還是取值大。當r＝5時，且當參數p取值范圍從11到59時，陣列碼c(p-5,5,p)、柯西循環碼和crs碼的單位解碼計算復雜度如圖3。與r等于4的情況類似，crs碼的解碼計算復雜度隨著參數p的增加而變大，而陣列碼c(p-5,5,p)和柯西循環碼的計算復雜度則隨著參數p的增加而變小。在所有測試的數據點，陣列碼c(p-5,5,p)的解碼計算復雜度均是最低的。當參數p大于47時，crs碼的解碼計算復雜度大于循環柯西碼的解碼計算復雜度。相反，當參數p小于47時，crs碼的解碼計算復雜度則小于循環柯西碼的解碼計算復雜度。陣列碼c(k,r,p)相比于其他mds碼，如crs碼，最大的優勢在于其編碼計算復雜度和解碼計算復雜度都低很多，而且對于原始信息數據塊的數量沒有固定，可取2到p內的任意整數。相比于能恢復兩個結點的evenodd碼，陣列碼c(k,r,p)在編解碼復雜度幾乎不變的情況下，提高了系統的容錯性，最多能修復任意r個節點失效。陣列碼c(k,r,p)擁有較優的編解碼復雜度，同時大大提升了系統的容錯能力，而且對原始信息數據塊的數量沒有固定，可取2到p內的任意整數，更加靈活，達到存儲開銷與系統可靠性的最優折中。以上內容是結合具體的優選實施方式對本發明所作的進一步詳細說明，不能認定本發明的具體實施只局限于這些說明。對于本發明所屬
技術領域：
的普通技術人員來說，在不脫離本發明構思的前提下，還可以做出若干簡單推演或替換，都應當視為屬于本發明的保護范圍。當前第1頁12