一種風電接入的電力系統等值簡化方法與流程

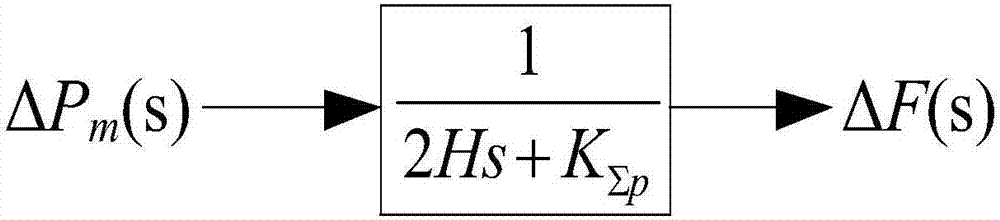
本發明涉及電力系統
技術領域：
，特別是涉及一種風電接入的電力系統等值簡化方法。
背景技術：
：近年來，風電已經成為世界上發展最快的新能源發電方式。電力系統中風電滲透率逐漸提高。由于雙饋機組(3型)和全整流型風電機組(4型)具有故障率低、可靠性強、功率調節方便等優點，已逐漸成為風力發電的主流機型。這兩種風電機組通過換流器并網，風電機組的轉速以及輸出功率隨著風速變化而變化，與電網頻率解耦。但當電力系統突然失去發電機組時，這兩種風電機組不能像常規同步機組依靠機組的大慣性響應能力和一次調頻備用容量滿足頻率響應指標要求。隨著電力系統風電滲透率的升高，電力系統的頻率響應能力將逐漸下降，頻率穩定性將迎來很大挑戰。因此，對實際系統頻率響應的評估顯得尤為重要。時域仿真法(逐步積分法)可用于評估系統的頻率響應。該方法將電力系統各元件之間的拓撲關系形成全系統模型，建立一組微分方程組，以穩態工況和潮流解為初值，求解擾動下的數值解，逐步求得系統狀態變量和代數變量隨時間的變化曲線。這種方法適用于大規模的電力系統，可適用于各種元件模型。但是全系統時域仿真逐步積分計算速度較慢，仿真時間較長，評估的效率較低。為解決以上問題，文獻《alow-ordersystemfrequencyresponsemodel》提出了將實際電力系統用等值簡化模型代替的思想，并具有一定的精度。但該文獻提出的等值簡化模型僅僅適用于純汽輪機和調速器模型的電力系統。文獻《含風電的電力系統頻率動態分析》提出了風電參與的頻率調節系統等值簡化模型。但是并沒有給出模型的具體等值方法，以及等值簡化模型參數的聚合方法，也沒有給出等值簡化模型在不同場景下的等值精度。技術實現要素：針對現有技術中存在不足，本發明提供了一種風電接入的電力系統等值簡化方法，本發明是通過以下技術手段實現上述技術目的的。一種風電接入的電力系統等值簡化方法，其特征在于，包括如下步驟：步驟1：建立實際電力系統的等值簡化模型；實際電力系統的等值簡化模型由發電機及負荷模型、汽輪機和調速器模型、水輪機和調速器模型、風電機組模型的等值簡化模型構成；所述發電機及負荷模型的等值簡化模型搭建方法為：將發電機及負荷模型中的負荷以靜態數學模型表示為：其中，pn為基準點穩態運行負荷有功功率，qn為基準點穩態運行負荷無功功率；p為負荷實際有功功率；q為負荷實際無功功率；δf為系統頻率與額定頻率fn的偏差；a0為恒功率有功負荷功率占總有功功率的百分比；a0′為恒功率無功負荷功率占總無功功率的百分比；a1為恒電流有功負荷功率占總有功功率的百分比；a'1為恒電流無功負荷功率占總無功功率的百分比；a2為恒阻抗有功負荷功率占總有功功率的百分比；a'2為恒阻抗無功負荷功率占總無功功率的百分比；kσp為負荷有功頻率調節效應系數；kσq為負荷無功頻率調節系數；a0+a1+a2＝1；a'0+a'1+a'2＝1；當實際電力系統中有n組發電機及負荷模型時，將n組發電機及負荷模型等效為一組發電機及負荷模型，實際電力系統的功率平衡關系為：對上式進行拉普拉斯變換可得：發電機及負荷等值簡化模型傳遞函數為：上式中，δpm為實際電力系統等值發電機機械功率的變化；δpe為實際電力系統等值發電機電磁功率的變化；kσ為實際電力系統負荷的頻率調節效應系數；fave為平均頻率，h為實際電力系統總的慣性時間常數，δf為實際電力系統的頻率變化量，其中：式中，fave為平均頻率；fi為每臺機組工作頻率；hi為實際電力系統中每臺發電機的慣性時間常數；pmi為每臺發電機機械功率；pei為每臺發電機電磁功率，pm為實際電力系統中發電機總機械功率，pe為實際電力系統中發電機總電磁功率。所述汽輪機和調速器模型，其等值簡化模型搭建方法為：當實際電力系統中有n′組汽輪機和調速器模型時，將n′組汽輪機和調速器模型等效為一組汽輪機和調速器模型，傳遞函數如下：其中，tr是汽輪機等值再熱時間常數，fh為汽輪機高壓缸穩態輸出功率占汽輪機總輸出功率的比例，r為調速器等值調差系數，s為傳遞函數自變量；調速器等值調差系數r可等值計算如下：其中，ri為實際電力系統中每臺調速器調差系數；pni為實際電力系統中每臺發電機的額定容量。所述水輪機和調速器模型，其等值簡化模型為：當實際電力系統中有n″組水輪機和調速器模型時，將n″組水輪機和調速器模型等效為一組水輪機和調速器模型，傳遞函數如下：其中，tw是水輪機等值水流時間常數，tr是水輪機和調速器模型中調速器等值時間常數，rt為實際電力系統中暫態下降補償等值系數，r為調速器等值調差系數，s為傳遞函數自變量；當實際電力系統中有n″組水輪機和調速器模型時，實際電力系統中暫態下降補償等值系數rt計算如下：其中rti表示每組水輪機和調速器模型的暫態下降補償等值系數。所述風電機組模型，其等值簡化模型搭建方法為：當實際電力系統中有n″′組風電機組模型時，將n″′組風電機組模型等效為一組風電機組模型，則虛擬慣量控制和下垂控制增發的功率之和為：其中，hv為實際電力系統等值虛擬慣性時間常數，kv為等值下垂系數；δpmn3(t)是實際電力系統中風電機組虛擬慣量控制和下垂控制增發的有功功率。對上式進行拉普拉斯變換可得風電機組模型的傳遞函數：g2′(s)＝2hvs+kv。步驟2：根據聚合公式對實際電力系統的等值簡化模型的參數進行聚合；所述參數分別為汽輪機等值再熱時間常數tr、水輪機和調速器模型中的調速器等值時間常數tr、水輪機和調速器模型中的水輪機等值水流時間常數tw，所述聚合公式為：其中，n′、n″分別表示實際電力系統中的汽輪機和調速器模型、水輪機和調速器模型以的數量。步驟3：計算實際電力系統的等值簡化模型的調頻能力；所述實際電力系統的等值簡化模型的調頻能力的計算公式為：其中，pmi為實際電力系統中具備一次調頻能力的每臺原動機輸出功率，km1、km2、km3分別表示實際電力系統中汽輪機和調速器模型、水輪機和調速器模型以及風電機組模型的調頻能力。步驟4：計算實際電力系統的等值簡化模型的穩態頻率偏差和頻率初始下降率；切除實際電力系統中一臺發電機，則實際電力系統有功缺額δpa，δpa(s)＝δpa/s；則實際電力系統的頻率偏差δf為：其中，g1(s)、g2(s)、g3(s)、g4(s)分別為發電機及負荷模型、風電機組模型、水輪機和調速器模型、汽輪機和調速器模型參與實際電力系統頻率調節的傳遞函數；根據終值定理，實際電力系統的等值簡化模型的穩態頻率偏差δf為:式中，kt＝km1+km2+r·kv·km3；發電機提供的功率δpm為：根據上式可求得實際電力系統的等值簡化模型的頻率初始下降率：本發明的有益效果在于：1、所建立的實際電力系統的等值簡化模型可代替實際電力系統，從而將復雜的實際電力系統簡化。實現了通過簡單模型來研究復雜系統的效果。2、所建立的實際電力系統的等值簡化模型在頻率響應評估時，可以大大減小計算規模。很大程度上縮短了全系統時域仿真的時間，提高了評估效率。3、所建立的實際電力系統的等值簡化模型在進行參數聚合時，以汽輪機和調速器模型、的功率為基準進行加權聚合，很大程度上提高了等值的可信度與精確性。4、提出的實際電力系統的實際電力系統中各模型調頻能力的計算方法，改進了傳統的粗略計算方法，使得等值簡化模型在進行頻率響應評估時與實際電力系統更加接近，更加精確。5、所建立的實際電力系統的等值簡化模型適用于發電機及負荷模型、汽輪機和調速器模型、水輪機和調速器模型、風電機組模型頻率調節的研究，適用范圍較廣。附圖說明圖1為本發明所述的實際電力系統的發電機及負荷模型的等值簡化模型。圖2為本發明所述的實際電力系統的汽輪機和調速器模型的等值簡化模型。圖3為本發明所述的實際電力系統的水輪機和調速器模型的等值簡化模型。圖4為本發明所述的實際電力系統的風電機組模型參與調頻的等值簡化模型。圖5為本發明所述的實際電力系統的風電機組模型的等值簡化模型。圖6為本發明所述的實際電力系統的等值簡化模型。圖7為本發明所述的實際電力系統。具體實施方式下面結合附圖以及具體實施例對本發明作進一步的說明，但本發明的保護范圍并不限于此。一種風電接入的電力系統等值簡化方法，其特征在于，包括如下步驟：步驟1：如圖6所示，建立實際電力系統的等值簡化模型；實際電力系統的等值簡化模型由發電機及負荷模型、汽輪機和調速器模型、水輪機和調速器模型、風電機組模型的等值簡化模型構成；如圖1所示，所述發電機及負荷模型的等值簡化模型搭建方法為：將發電機及負荷模型中的負荷以靜態數學模型表示為：其中，pn為基準點穩態運行負荷有功功率，qn為基準點穩態運行負荷無功功率；p為負荷實際有功功率；q為負荷實際無功功率；δf為系統頻率與額定頻率fn的偏差；a0為恒功率有功負荷功率占總有功功率的百分比；a′0為恒功率無功負荷功率占總無功功率的百分比；a1為恒電流有功負荷功率占總有功功率的百分比；a'1為恒電流無功負荷功率占總無功功率的百分比；a2為恒阻抗有功負荷功率占總有功功率的百分比；a'2為恒阻抗無功負荷功率占總無功功率的百分比；kσp為負荷有功頻率調節效應系數；kσq為負荷無功頻率調節系數；a0+a1+a2＝1；a'0+a'1+a'2＝1；負荷以靜態數學模型表示反映了當實際電力系統頻率變化時，負荷的有功功率、無功功率隨電壓和頻率變化的規律。當實際電力系統中有n組發電機及負荷模型時，將n組發電機及負荷模型等效為一組發電機及負荷模型，實際電力系統的功率平衡關系為：對上式進行拉普拉斯變換可得：發電機及負荷等值簡化模型傳遞函數為：上式中，δpm為實際電力系統等值發電機機械功率的變化；δpe為實際電力系統等值發電機電磁功率的變化；kσ為實際電力系統負荷的頻率調節效應系數；fave為平均頻率，h為實際電力系統總的慣性時間常數，δf為實際電力系統的頻率變化量，其中：式中，fave為平均頻率；fi為每臺機組工作頻率；hi為實際電力系統中每臺發電機的慣性時間常數；pmi為每臺發電機機械功率；pei為每臺發電機電磁功率，pm為實際電力系統中發電機總機械功率，pe為實際電力系統中發電機總電磁功率。如圖2所示，所述汽輪機和調速器模型，其等值簡化模型搭建方法為：汽輪機和調速器模型最主要的環節，就是利用液壓原理控制汽輪機汽門開度的執行環節，調節汽輪機的輸入功率。若實際電力系統只進行一次調頻，則調速器等值調差系數r起主導作用，當實際電力系統中有n′組汽輪機和調速器模型時，將n′組汽輪機和調速器模型等效為一組汽輪機和調速器模型，傳遞函數如下：其中，tr是汽輪機等值再熱時間常數，fh為汽輪機高壓缸穩態輸出功率占汽輪機總輸出功率的比例，r為調速器等值調差系數，s為傳遞函數自變量；調速器等值調差系數r可等值計算如下：其中，ri為實際電力系統中每臺調速器調差系數；pni為實際電力系統中每臺發電機的額定容量。如圖3所示，所述水輪機和調速器模型，其等值簡化模型為：水輪機和調速器模型是通過控制水輪機水門的開度，從而調節水輪機的輸入功率的目的。在實際電力系統中，水輪機和調速器模型中調速器等值時間常數tr和調速器等值調差系數r對實際電力系統的頻率調節起到主導作用，在對水輪機和調速器模型進行等值簡化模型建立時，可只考慮tr和r。當實際電力系統中有n″組水輪機和調速器模型時，將n″組水輪機和調速器模型等效為一組水輪機和調速器模型，傳遞函數如下：其中，tw是水輪機等值水流時間常數，tr是水輪機和調速器模型中調速器等值時間常數，rt為實際電力系統中暫態下降補償等值系數，r為調速器等值調差系數，s為傳遞函數自變量；當實際電力系統中有n″組水輪機和調速器模型時，實際電力系統中暫態下降補償等值系數rt計算如下：其中，rti表示每組水輪機和調速器模型的暫態下降補償等值系數。如圖5所示，所述風電機組模型，其等值簡化模型搭建方法為：當出現大規模風電機組模型并網時，實際電力系統頻率穩定性將面臨很大挑戰。為解決這個問題，可以通過實際電力系統頻率偏差δf的下垂控制和頻率變化率df/dt的虛擬慣量控制來模擬風電機組模型的等值簡化模型的慣性響應和一次調頻，風電機組模型的等值簡化模型的控制環節仍然包含df/dt微分環節和δf比例環節兩個部分，df/dt微分環節和δf比例環節分別對實際電力系統的頻率變化率和頻率偏差起作用，調節原理如圖4所示。當實際電力系統中有n″′組風電機組模型時，將n″′組風電機組模型等效為一組風電機組模型，則虛擬慣量控制和下垂控制增發的功率之和為：其中，hv為實際電力系統等值虛擬慣性時間常數，kv為等值下垂系數；δpmn3(t)是實際電力系統中風電機組虛擬慣量控制和下垂控制增發的有功功率。對上式進行拉普拉斯變換可得風電機組模型的傳遞函數：g2′(s)＝2hvs+kv。步驟2：根據聚合公式對實際電力系統的等值簡化模型的參數進行聚合；所述參數分別為汽輪機等值再熱時間常數tr、水輪機和調速器模型中的調速器等值時間常數tr、水輪機和調速器模型中的水輪機等值水流時間常數tw，所述聚合公式為：其中，n′、n″分別表示實際電力系統中的汽輪機和調速器模型、水輪機和調速器模型以的數量。步驟3：計算實際電力系統的等值簡化模型的調頻能力；所述實際電力系統的等值簡化模型的調頻能力的計算公式為：其中，pmi為實際電力系統中具備一次調頻能力的每臺原動機輸出功率，km1、km2、km3分別表示實際電力系統中汽輪機和調速器模型、水輪機和調速器模型以及風電機組模型的調頻能力。步驟4：計算實際電力系統的等值簡化模型的穩態頻率偏差和頻率初始下降率；切除實際電力系統中一臺發電機，則實際電力系統有功缺額δpa，δpa(s)＝δpa/s；則實際電力系統的頻率偏差δf為：其中，g1(s)、g2(s)、g3(s)、g4(s)分別為發電機及負荷模型、風電機組模型、水輪機和調速器模型、汽輪機和調速器模型參與實際電力系統頻率調節的傳遞函數；根據終值定理，實際電力系統的等值簡化模型的穩態頻率偏差δf為:式中，kt＝km1+km2+r·kv·km3；發電機提供的功率δpm為：根據上式可求得實際電力系統的等值簡化模型的頻率初始下降率：實施例在pss/e34.1軟件中搭建實際電力系統，進行仿真分析。對比不同情形下所建立的等值簡化模型與實際電力系統頻率特性。實際電力系統如圖7所示。研究實際電力系統中的含有汽輪機和調速器模型、水輪機和調速器模型、風電機組模型，以及發電機及負荷模型在不同案例下所建立的等值簡化模型，并檢測實際電力系統頻率響應評估的正確性。具體情形如下表。表一：6組研究案例表二：實際電力系統和實際電力系統的等值簡化模型的最低點頻率及最低點頻率的相對誤差研究案例案例1案例2案例3等值簡化模型49.7980hz49.7532hz49.6434hz實際電力系統49.8135hz49.7711hz49.6524hz相對誤差8.31％7.82％2.59％研究案例案例4案例5案例6等值簡化模型49.6981hz49.7051hz49.7483hz實際電力系統49.7004hz49.7041hz49.7409hz相對誤差2.56％0.34％2.86％表三：實際電力系統和實際電力系統的等值簡化模型的穩態頻率及穩態頻率的相對誤差表四：實際電力系統和實際電力系統的等值簡化模型的頻率評估時間研究案例案例1案例2案例3等值簡化模型2.52s2.30s2.20s實際電力系統24.60min25.90min26.50min研究案例案例4案例5案例6等值簡化模型2.30s2.55s2.174s實際電力系統28.51min30.87min33.10min表一給出了6組不同研究案例，表二給出了每組研究案例實際電力系統及其等值簡化模型的最低點頻率、實際電力系統與其等值簡化模型之間的最低點頻率的相對誤差，表三給出了實際電力系統和實際電力系統的等值簡化模型的穩態頻率及穩態頻率的相對誤差，可以看出實際電力系統與其等值簡化模型之間，無論是最低點頻率的相對誤差還是穩態頻率的相對誤差均控制在10％以內；如表四所示，實際電力系統和實際電力系統的等值簡化模型的頻率評估時間，可知，實際電力系統的頻率評估時間遠大于實際電力系統的等值簡化模型的頻率評估時間。由此，可知本發明所述的實際電力系統的等值簡化模型具有較高的精度，并大大減少全系統時域仿真的時間，提高了評估效率，很大程度上提高了評估效率。所述實施例為本發明的優選的實施方式，但本發明并不限于上述實施方式，在不背離本發明的實質內容的情況下，本領域技術人員能夠做出的任何顯而易見的改進、替換或變型均屬于本發明的保護范圍。當前第1頁12