基于場景解耦和異步迭代的多目標隨機動態經濟調度方法與流程

本發明涉及一種用于省級電力系統日前運行調度的基于場景解耦和異步迭代的多目標隨機動態經濟調度方法，屬于電氣工程技術領域。

背景技術：

風電場接入電力系統后的動態經濟調度問題實際上是一個隨機優化問題。這方面早期的研究是利用機會約束模型和魯棒優化模型。機會約束模型考慮隨機性不夠精確，而魯棒優化模型的計算結果偏于保守。近期，美國阿貢國家實驗室對隨機規劃的相關研究的思路是采用場景樹模型生成大量隨機誤差場景，用巨型計算機對該問題進行精確計算。目前，國內電網有功調度執行的是節能發電調度模式，目標函數只有一個或是幾個目標函數的加權和。調度運行方式需要兼顧經濟性和環保性，但有時這兩個目標會互相沖突，即，只考慮某個目標時，另一個目標就無法達到較優的指標。所以在經濟調度模型中同時優化兩個及兩個以上目標函數的做法能為調度員或決策者帶來方便。

將基于場景法的隨機動態經濟調度模型當應用到中國某省級電網時，用蒙特卡洛法生成1000個采樣場景，變量數達到了16,432,417；等式約束數量為99,101；不等式約束數量為115,319,756，即使采用關鍵線路搜索法處理網絡約束，不等式約束數量也為49,686,237。這個非線性規劃問題的規模仍然十分巨大。如果要為電網調度中心提供方便而考慮多目標問題時，計算規模進一步擴大。但是，采用一些商業軟件如gams/conopt求解器或傳統內點法均不能求解這個問題。

技術實現要素：

針對現有技術的不足，本發明提出了一種基于場景解耦和異步迭代的多目標隨機動態經濟調度方法，其能夠有效求解省級電力系統的多目標隨機動態調度問題。

本發明解決其技術問題采取的技術方案是：一種基于場景解耦和異步迭代的多目標隨機動態經濟調度方法，它包括以下步驟：

1)給定相關計算參數；

2)建立多目標隨機動態經濟調度模型；

3)采用場景解耦和異步迭代改進內點法求解多目標隨機動態經濟調度模型。

進一步地，在步驟1)中，所述相關計算參數包括常規發電機組成本系數及出力上下限參數，輸電支路阻抗及容量參數，抽水蓄能機組運行參數，以及電力系統的負荷和風電功率參數。

進一步地，其特征是，在步驟2)中，

所述多目標隨機動態經濟調度模型中的目標函數為：

①購電費用

第一個目標是最小化預測場景的購電費用，定義如下：

其中，ag是第g^th臺常規機組的購電費用；awind是風電場的購電費用；為預測場景中第g^th臺機組在時段t的出力；為預測場景中第w^th個風電場在時段t的調度出力；ng和nw是常規機組臺數和系統的并網風電場個數；

②污染氣體排放量

第二個目標是最小化常規機組的污染氣體排放量，定義如下：

其中，b2,g，b1,g和b0,g是第g^th臺常規機組的排放系數；所述常規機組的污染氣體至少包括so2和nox氣體；

所述多目標隨機動態經濟調度模型中的基本約束為：

①功率平衡約束：

忽略有功網損，預測場景和誤差場景中的有功功率平衡約束定義如下：

其中，是預測場景和誤差場景中第g^th臺常規機組的在時段t的出力；為預測場景和誤差場景中第w^th個風電場在時段t的調度出力；pmt為負荷節點m在時段t的負荷；nd是負荷節點數目，t和ns均為正整數；

②常規機組出力約束：

a)預測場景和誤差場景中的常規機組出力上下限約束，表達如下：

其中，pgmax和pgmin是第g^th臺常規機組的出力上下限；

b)預測場景和誤差場景中的爬坡/滑坡約束，表達如下：

其中，rug和rdg分別是第g^th臺常規機組的爬坡/滑坡系數；δt為動態調度兩相鄰時刻的時間間隔；

c)場景轉移約束

場景轉移約束表示從預測場景到誤差場景，常規機組的可調度裕度，表達如下：

其中，δt’為第g^th臺常規機組為適應風電出力預測誤差所需的調度響應時間；

③風場出力約束：

當系統備用不足或是由于靠近風場的并網處的線路傳輸容量的限制，棄風是不可避免的，所以風場出力約束表達如下：

④抽水蓄能電站的相關約束：

抽水蓄能機組每個時刻只能在發電、抽水和停機中其中一種工況下工作，表達如下：

其中，和分別表示第r^th座抽蓄電站在t時段的發電和抽水功率；prgmax和prpmax分別表示分別表示第r^th座抽蓄電站相應的發電和抽水功率上限；nps表示抽蓄電站的數量；

⑤網絡傳輸約束：

預測場景和誤差場景中電網線路上的有功傳輸上下限約束表示為：

其中，plmax為線路l的最大傳輸容量上限；nl為線路條數；為預測場景和誤差場景中線路l上時段t的傳輸功率。

進一步地，在常規機組出力約束條件中，動態調度兩相鄰時刻的時間間隔δt為15分鐘，第g^th臺常規機組為適應風電出力預測誤差所需的調度響應時間δt’為15分鐘。

進一步地，在抽水蓄能電站的相關約束條件中，抽水消耗電量和發出電量的平衡關系約束可表示為：

其中，抽水和發電之間有能量損耗，ξ為能量轉換效率參數，取ξ＝75％；

網絡傳輸約束條件采用直流潮流模型表示為：

其中，glg，flw，hlg和dld分別代表線路l與常規機組，風電場，抽蓄電站和負荷之間的有功功率傳輸因子。

進一步地，多目標隨機動態經濟調度模型的緊湊表達形式為：

minf(x⁰)＝{f1(x⁰),f2(x⁰)}(12)

s.t.g0(x⁰)＝0(13)

gs(x^s)＝0s＝1,2,...,ns(14)

其中，f1(·)和f2(·)分別為目標函數(1)和目標函數(2)；x⁰表示預測場景中常規機組、風電場和抽水蓄能電站出力向量；x^s表示誤差場景中常規機組、風電場和抽水蓄能電站出力向量；式(13)表示預測場景中的等式約束，即s＝0時的式(3)、式(8)和式(9)；式(14)表示誤差場景中的等式約束，即s＝1,2,…,ns時的式(3)、式(8)和式(9)；式(15)代表式式(4)-式(7)、式(10)以及式(8)中的不等式約束。

進一步地，所述步驟3)包括以下步驟：

31)從兩目標問題向單目標問題的轉化；

32)采用內點法求解單目標問題；

33)采用場景解耦和異步迭代求解修正方程；

34)并行求解最優解。

進一步地，所述步驟31)的具體過程為：

①目標函數的規格化：

由于兩個目標函數具有不同的量綱，做如下規格化處理：

其中，和表示兩規格化的目標函數；f1(x^1*)和f2(x^2*)表示最優解，即烏托邦點；f1(x^2*)和f2(x^1*)表示目標空間中的最劣解；

②生成烏托邦線上均勻分布的點：

假設把烏托邦線分成m段，烏托邦線上的等距離點按照如下公式生成：

其中，β1和β2是兩端點的權重系數，j＝0,1,2,...,m：

其中，m＝20；

③搜索均勻分布的帕累托最優解

通過由式(17)產生的等距點的法向量與帕累托前沿相交，得到均勻分布的帕累托最優解，法向量是從烏托邦線上到帕累托前沿上點的向量，法向量的表達式如下：

其中，e＝[1,1]^t；

進一步推導，帕累托前沿上的點由下式表示：

其中，λ表示和之間的距離；

帕累托點可由求解以下單目標模型得到：

min(-λ)(21)

g0(x⁰)＝0(23)

gs(x^s)＝0s＝1,2,...,ns(24)

如果點沿著烏托邦線移動，通過求解由式(21)～式(25)組成的單目標問題來獲得一組均勻分布的點，這些點就是帕累托最優解，其中，j＝0,1,2,…,20。

進一步地，所述步驟32)的具體過程為：

合并式(22)和式(23)，并且對不等式(25)引入松弛變量sh，sh≥0，由式(21)～式(25)組成的單目標問題改寫成以下形式：

min(-λ)(26)

s.t.g(x⁰,λ)＝0(27)

gs(x^s)＝0s＝1,2,...,ns(28)

非線性原對偶內點法中的增廣拉格朗日函數表示如下：

其中，y、ys和yh為拉格朗日乘子向量；nh是式(29)中不等式約束的數量；μ是壁壘參數，μ≥0；s＝1,2,…,ns。

根據karush-kuhn-tucker最優性條件，對增廣拉格朗日函數式(30)求偏導，得到一組非線性方程組，再用牛頓法求解可得到簡化修正方程組；

按預測場景和誤差場景的順序對簡化后的修正方程和變量進行排序，得到如下其系數矩陣具有對角加邊結構的簡化修正方程組：

其中，δz0＝[(δx⁰)^t,(δy)^t,δλ]^t；δzs＝[(δx^s)^t,(δys)^t]^t；l0、ls和ms是對稱稀疏矩陣；s＝1,2,…,ns。

進一步地，所述步驟33)的具體過程為：

將式(31)方程等效地解耦為ns+1個低維的方程組，即：

運用同步迭代的方法將式(32)和式(33)轉化為如下形式：

式中，s＝1,2,…,ns。

進一步地，所述步驟34)的具體過程為：首先根據nbi法計算兩個端點，然后再計算烏托邦線上其它點的帕累托最優解。

本發明的有益效果如下：

本發明對系數矩陣具有對角加邊形式的高維修正方程進行場景解耦，將高維修正方程的求解等價分解為若干個(分別與預測場景與采樣場景對應)低維線性方程的求解。在求解這些低維線性方程時采用異步迭代技術，從而避免產生稠密矩陣，使得整個計算過程中矩陣都是稀疏的，并實施并行計算。

本發明采用法線邊界交叉(nbi)法和內點法求解多目標優化調度問題，較好地兼顧了電網運行的經濟性和環保性，是一個具有較高運行效益的調度方案。

本發明利用場景法將多目標隨機動態經濟調度問題轉化為大規模多目標確定性動態經濟調度問題，再借助法線邊界交叉(nbi)法將其轉化為一系列大規模單目標非線性規劃問題，并用非線性原對偶內點法求解。在應用非線性原對偶內點法求解這些大規模單目標非線性規劃問題過程中，按照場景順序排列的簡化修正方程的系數矩陣具有對角加邊結構。因此可對其實施解耦，并采用異步塊迭代法對解耦后的低維修正方程組進行求解，可應用于求解某省級電力系統的多目標隨機動態調度問題。

附圖說明

圖1為本發明的方法流程圖；

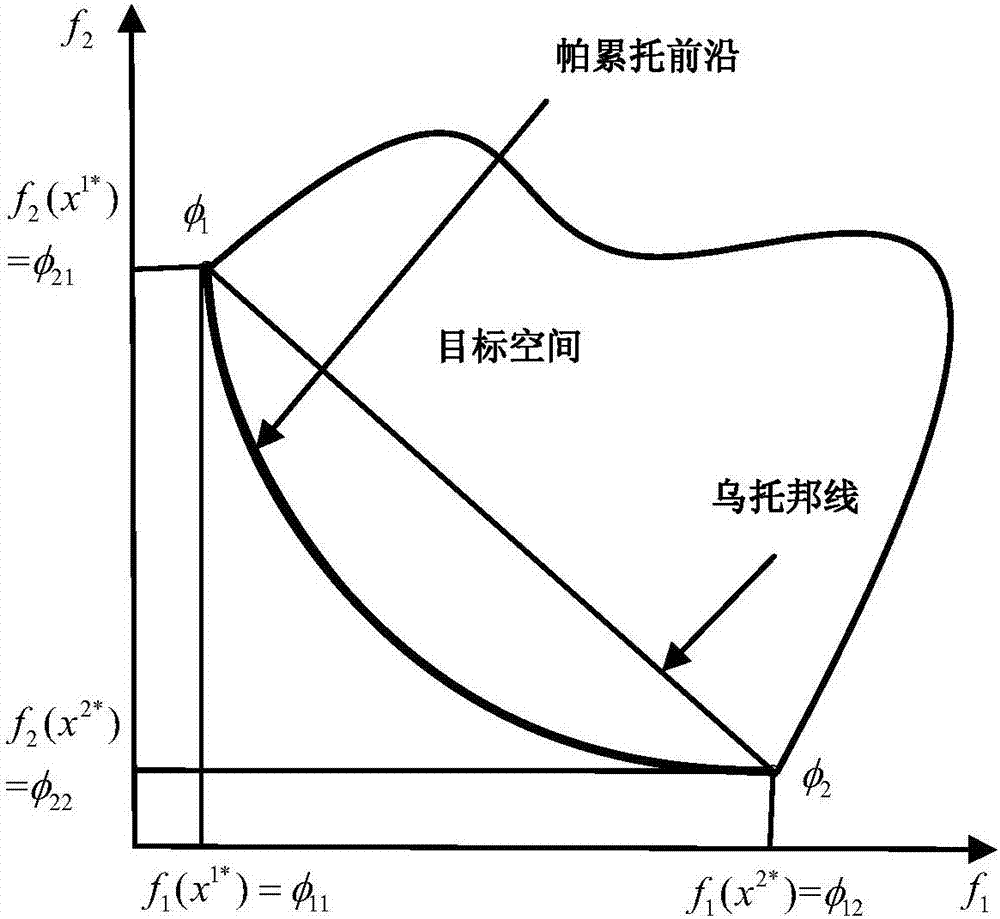
圖2為目標空間中的帕累托前沿和烏托邦線示意圖；

圖3為規格化目標空間中的帕累托前沿和烏托邦線示意圖；

圖4為帕累托前沿上最優解的求解順序示意圖；

圖5為單個帕累托最優解的并行計算架構示意圖。

具體實施方式

為能清楚說明本方案的技術特點，下面通過具體實施方式，并結合其附圖，對本發明進行詳細闡述。下文的公開提供了許多不同的實施例或例子用來實現本發明的不同結構。為了簡化本發明的公開，下文中對特定例子的部件和設置進行描述。此外，本發明可以在不同例子中重復參考數字和/或字母。這種重復是為了簡化和清楚的目的，其本身不指示所討論各種實施例和/或設置之間的關系。應當注意，在附圖中所圖示的部件不一定按比例繪制。本發明省略了對公知組件和處理技術及工藝的描述以避免不必要地限制本發明。

如圖1所示，本發明的一種基于場景解耦和異步迭代的多目標隨機動態經濟調度方法，它包括以下步驟：

1)給定相關計算參數；

2)建立多目標隨機動態經濟調度模型；

3)采用場景解耦和異步迭代改進內點法求解多目標隨機動態經濟調度模型。

在步驟1)中，所述相關計算參數包括常規發電機組成本系數及出力上下限參數，輸電支路阻抗及容量參數，抽水蓄能機組運行參數，以及電力系統的負荷和風電功率參數。

在步驟2)中，優化調度模型中的目標函數為：

①購電費用

第一個目標是最小化預測場景的購電費用，定義如下：

其中，ag是第g^th臺常規機組的購電費用；awind是風電場的購電費用；為預測場景中第g^th臺機組在時段t的出力；為預測場景中第w^th個風電場在時段t的調度出力；ng和nw是常規機組臺數和系統的并網風電場個數。

②污染氣體排放量

第二個目標是最小化常規機組的污染氣體排放量(以為so2，nox主)，定義如下：

其中，b2,g，b1,g和b0,g是第g^th臺常規機組的排放系數。

所述步驟(2)中，優化調度模型中的基本約束為：

①功率平衡約束：

忽略有功網損，預測場景和誤差場景中的有功功率平衡約束定義如下：

其中，是預測場景和誤差場景中第g^th臺常規機組的在時段t的出力；為預測場景和誤差場景中第w^th個風電場在時段t的調度出力；pmt為負荷節點m在時段t的負荷；nd是負荷節點數目。

②常規機組出力約束：

a)預測場景和誤差場景中的常規機組出力上下限約束，表達如下：

其中，pgmax和pgmin是第g^th臺常規機組的出力上下限。

b)預測場景和誤差場景中的爬坡/滑坡約束，表達如下：

其中，rug和rdg分別是第g^th臺常規機組的爬坡/滑坡系數；δt為動態調度兩相鄰時刻的時間間隔，在具體實施過程中，δt取15分鐘。

c)場景轉移約束

該約束表示從預測場景到誤差場景，常規機組的可調度裕度，表達如下：

其中，δt’為第g^th臺常規機組為適應風電出力預測誤差所需的調度響應時間，在具體實施過程中，δt’取15分鐘。

③風場出力約束：

當系統備用不足或是由于靠近風場的并網處的線路傳輸容量的限制，棄風是不可避免的。所以，風場出力約束表達如下：

④抽水蓄能電站的相關約束：

抽水蓄能機組每個時刻只能在一種工況下工作：發電，抽水，停機。在數學表達上如下所示：

其中，和分別表示第r^th座抽蓄電站在t時段的發電和抽水功率；prgmax和prpmax分別表示分別表示第r^th座抽蓄電站相應的發電和抽水功率上限；nps表示抽蓄電站的數量。

在實際運行中，不僅要滿足出力上下限約束，還要確保一天中的發電量和抽水量匹配，即抽水消耗電量和發出電量要平衡。發抽(抽水消耗電量和發出電量)平衡的關系約束可表示為：

其中，抽水和發電之間有能量損耗，ξ為能量轉換效率參數，在具體實施過程中，取ξ＝75％。

⑤網絡傳輸約束：

預測場景和誤差場景中電網線路上的有功傳輸上下限約束可表示為：

其中，plmax為線路l的最大傳輸容量上限；nl為線路條數；為預測場景和誤差場景中線路l上時段t的傳輸功率。約束采用直流潮流模型表示為：

其中，glg，flw，hlg和dld分別代表線路l與常規機組，風電場，抽蓄電站和負荷之間的有功功率傳輸因子。

由式(1)～式(11)描述的多目標隨機動態經濟調度模型可以改寫成以下緊湊表達形式：

minf(x⁰)＝{f1(x⁰),f2(x⁰)}(12)

s.t.g0(x⁰)＝0(13)

gs(x^s)＝0s＝1,2,...,ns(14)

其中，f1(·)和f2(·)表示兩個目標函數方程(1)～(2)；x⁰表示預測場景中常規機組，風電場和抽水蓄能電站出力向量；x^s(s＝1,2,…,ns)表示誤差場景中常規機組，風電場和抽水蓄能電站出力向量；式(13)表示預測場景中的等式約束，即s＝0時的式(3)，(8)和(9)；式(14)表示誤差場景中的等式約束，即s＝1,2,…,ns時的式(3)，(8)和(9)；式(15)代表式(4)-(7)，(10)以及(8)中的不等式約束。

所述步驟3)包括以下步驟：

(1)從兩目標問題向單目標問題的轉化

2顯示了式(12)～(15)所描述的兩目標問題的目標空間中的帕累托前沿和烏托邦線，目標函數f1和f2是坐標系的兩軸。x^1*和x^2*表示兩個單目標優化問題的最優解，對應圖中兩點φ1(f1(x^1*),f2(x^1*))和φ2(f1(x^2*),f2(x^2*))。這兩個單目標問題為在考慮約束(12)～(15)的情況下分別最小化f1和f2。φ1和φ2組成了帕累托前沿的兩個端點，它們的連線叫做烏托邦線。

①目標函數的規格化：

由于兩個目標函數具有不同的量綱，為避免產生數值問題，目標空間需要做如下規格化處理：

其中，和表示兩規格化的目標函數；f1(x^1*)和f2(x^2*)表示最優解，即，烏托邦點；f1(x^2*)和f2(x^1*)表示目標空間中的最劣解。

所以規格化以后目標函數的范圍為[0,1]，如圖3所示。

②生成烏托邦線上均勻分布的點：

如圖3所示，是從到的向量。假設把烏托邦線分成m段，烏托邦線上的等距離點按照如下公式生成：

其中，β1和β2是兩端點的權重系數：

在具體實施過程中，m設為20，這樣烏托邦線上就有21個等距離點。

③搜索均勻分布的帕累托最優解

通過由式(17)產生的等距點的法向量與帕累托前沿相交，我們就能得到均勻分布的帕累托最優解。圖3中，法向量是從烏托邦線上到帕累托前沿上點的向量，表達式如下：

其中，e＝[1,1]^t。

進一步推導，帕累托前沿上的點可由下式表示：

其中，λ表示和之間的距離；

綜上所述，原多目標問題轉化為了一系列單目標問題。帕累托點yj可由求解以下單目標模型得到：

min(-λ)(21)

g0(x⁰)＝0(23)

gs(x^s)＝0s＝1,2,...,ns(24)

如果點沿著烏托邦線移動，通過求解由式(21)～(25)組成的單目標問題來獲得一組均勻分布的點，這些點就是帕累托最優解。

(2)采用內點法求解單目標問題

合并式(22)和(23)，并且對不等式(25)引入松弛變量sh(sh≥0)。那么，由式(21)～(25)組成的單目標問題可以改寫成以下形式：

min(-λ)(26)

s.t.g(x⁰,λ)＝0(27)

gs(x^s)＝0s＝1,2,...,ns(28)

非線性原對偶內點法中的增廣拉格朗日函數表示如下：

其中，y，ys(s＝1,2,…,ns)和yh為拉格朗日乘子向量；nh是式(29)中不等式約束的數量；μ是壁壘參數，μ≥0。

根據karush-kuhn-tucker(kkt)最優性條件，對增廣拉格朗日函數(30)求偏導，得到一組非線性方程組，再用牛頓法求解可得到簡化修正方程組。按預測場景和誤差場景的順序對簡化后的修正方程和變量進行排序，我們可得到如下其系數矩陣具有對角加邊結構^[88]的簡化修正方程組：

其中，δz0＝[(δx⁰)^t,(δy)^t,δλ]^t；δzs＝[(δx^s)^t,(δys)^t]^t(s＝1,2,…,ns)；l0，ls(s＝1,2,…,ns)和ms(s＝1,2,…,ns)是對稱稀疏矩陣。

此處需要注意的是，當求解兩端點與求解前沿上的其他帕累托點時，式(31)系數矩陣的維數是不同的，即，分別為(t·(ng+nw+2·nps)+t+nps+1)·(ns+1)和(t·(ng+nw+2·nps)+t+nps+1)·(ns+1)+3。當求解兩端點時，矩陣l0，ls和ms都是相同的，為t·(ng+nw+2·nps)+t+nps+1。但是當求解前沿上的其他帕累托點時，矩陣l0的維數變為t·(ng+nw+2·nps)+t+nps+4，此時矩陣ls和ms的維數不變。

(3)采用場景解耦和異步迭代求解修正方程：

雖然大型電力系統的多目標隨機動態經濟調度問題是一個高維模型，但是用內點法求解后，其系數矩陣具有對角加邊的特性。因此，可以將該方程等效地解耦為ns+1個低維的方程組，即：

運用同步迭代的方法將式(32)和(33)轉化為如下形式：

雖然l0，ls和ms都是稀疏矩陣且式(35)可以并行計算，但在第(k+1)次迭代時，計算式(34)中的稠密矩陣將占用大量的內存和cpu。這也是同步迭代的主要劣勢。然而，異步迭代^[92]可以避免這個劣勢。如果我們采用異步迭代求解式(32)和(33)，迭代中所用到的矩陣將都是稀疏的。假設初次迭代中δz0＝0，第(k+1)次迭代時，式(32)和(33)可轉化為如下形式：

顯然，式(37)也可以并行計算。

(4)并行求解最優解：

步驟3)中算法的編譯環境為matlab2014b，并行計算集群包括16臺dellm620刀片機。每臺刀片機配備至強e5-2650處理器(每塊處理器為8核8線程)128gb內存，還配備有infiniband網絡和萬兆光纖。infiniband網絡和萬兆光纖用于計算時的數據交換，文件共享和遠程控制。該集群操作系統為windowsserver2012r2。

根據建立的建立多目標隨機動態經濟調度模型，不同帕累托最優解之間的計算是相互獨立的。根據nbi法先計算兩端點，如圖4所示，首先根據nbi法計算兩個端點，然后再計算烏托邦線上其它點帕累托最優解。在計算帕累托最優解過程中采用并行線程進行求解。當求解單個帕累托最優解或兩端點中的其中一個時，按照圖5所示進行計算節點和頭節點中的數據交換過程，其中，nthr表示當求解單個帕累托最優解時所需的并行線程數量。

本發明對系數矩陣具有對角加邊形式的高維修正方程進行場景解耦，將高維修正方程的求解等價分解為若干個(分別與預測場景與采樣場景對應)低維線性方程的求解。在求解這些低維線性方程時采用異步迭代技術，從而避免產生稠密矩陣，使得整個計算過程中矩陣都是稀疏的，并可以實施并行計算。

本發明采用法線邊界交叉(nbi)法和內點法求解多目標優化調度問題，較好地兼顧了電網運行的經濟性和環保性，是一個具有較高運行效益的調度方案。

本發明所建立模型在由16個dellm620刀片機組成集群上進行仿真計算，并行實現了高維修正方程的場景解耦及異步迭代，該方法可以應用于省級電網的日前隨機經濟調度計算。

以上所述只是本發明的優選實施方式，對于本技術領域的普通技術人員來說，在不脫離本發明原理的前提下，還可以做出若干改進和潤飾，這些改進和潤飾也被視為本發明的保護范圍。