一種考慮負序分量的MMC系統簡化電磁暫態建模方法與流程
本發明屬于輸配電技術領域,尤其涉及一種考慮負序分量的mmc系統簡化電磁暫態建模方法。
背景技術:
電壓源換流器型直流輸電(voltagesourceconverterhighvoltagedirectcurrent,vsc-hvdc)在可再生能源并網、分布式發電并網、孤島供電、城市配網供電等方面具有較大的技術優勢,模塊化多電平換流器(modularmultilevelconverter,mmc)是vsc-hvdc拓撲的一種,具有模塊化設計、擴展性好、開關頻率低、波形質量好等優點,是目前vsc輸電工程實踐的主要拓撲結構。由于柔性直流輸電系統含有較高開關頻率的電力電子器件,詳細的電磁暫態仿真會受到仿真速度和規模的限制,因此研究適用于大規模交直流混聯系統的mmc簡化電磁暫態模型,不僅可以為系統穩定性研究提供基礎,還可為電網中長期規劃提供分析工具,具有重要的工程實際意義。
目前對mmc系統的簡化電磁暫態建模工作大部分基于穩態運行工況。當交流系統考慮負序電壓時,由于換流器的開關函數作用,mmc內部會產生正序、負序、零序分量,大大增加了mmc建模的復雜度。目前國內外提出的考慮負序分量的mmc系統簡化電磁暫態模型,沒有詳細考慮控制系統對mmc換流器的影響,或是忽略mmc內部詳細的動態過程。
技術實現要素:
針對上述問題,本發明提供了一種考慮負序分量的mmc系統簡化電磁暫態建模方法,包括:
步驟1、根據mmc的內部動態特性,確定abc靜止坐標系下考慮負序分量的mmc換流站內部子模塊電容電壓和橋臂電流的解析表達式;
步驟2、根據平均開關函數模型,建立dq旋轉坐標系下考慮負序分量的mmc換流站及其交直流系統的簡化電磁暫態模型;
步驟3、根據實際運行工況下的控制策略,建立包含相序分離環節、正序及負序電流矢量控制器的控制系統簡化電磁暫態模型;
步驟4、根據所述的mmc換流站及其交直流系統的簡化電磁暫態模型、控制系統簡化電磁暫態模型,建立得到考慮負序分離的mmc系統的簡化電磁模型。
所述步驟1中abc靜止坐標系下考慮負序分量的橋臂電流包括:直流分量、基頻正序、基頻負序、二倍頻正序、二倍頻負序、二倍頻零序分量,表達式如下:
式中,ipa、ina分別為a相上、下橋臂電流;idca為a相橋臂電流的直流分量;is+、is-、β1+、β1-分別為交流電流正序、負序分量的幅值和相角;icir+、icir-、icir0、β2+、β2-、β20分別為橋臂二倍頻正序、負序、零序電流的幅值和相角,ω為角頻率,t為時間。
所述abc靜止坐標系下考慮負序分量的mmc換流站內部子模塊電容電壓包括:直流分量、基頻正序、基頻負序、基頻零序、二倍頻正序、二倍頻負序、二倍頻零序分量,如下式所示:
式中,ucpa、ucna分別為a相子模塊上、下橋臂電容電壓,uc_dca為a相子模塊電容電壓的直流分量,uc1+、uc1-、uc10,uc2+、uc2-、uc20,θ1+、θ1-、θ10,θ2+、θ2-、θ20分別為基頻正序、基頻負序、基頻零序,二倍頻正序、二倍頻負序、二倍頻零序分量的幅值和相角,ω為角頻率,t為時間。
所述步驟2中開關函數模型如下式所示:
式中,s為平均開關函數,c為子模塊電容,uc為該橋臂子模塊電容電壓,iarm為橋臂電流,uarm為橋臂電壓,n為橋臂的子模塊級聯個數。
所述上、下橋臂的平均開關函數計算如下
式中,開關函數中的基頻負序分量是由于負序電流矢量控制疊加產生,sx中x=p,n,分別為上、下橋臂的平均開關函數,當上式中取兩個“-”號時,表示上橋臂的平均開關函數,取兩個“+”號表示下橋臂的平均開關函數,ω為角頻率;m+、m-分別為正序、負序調制比;ɑ+、ɑ-分別為a相基頻正負序分量的相角,b相、c相平均開關函數中基頻正序分量的相位依次滯后2π/3,而基頻負序分量依次超前2π/3。
所述的a相子模塊電容電壓的直流分量的簡化電磁暫態模型為:
所述的子模塊電容電壓基頻正序分量的簡化電磁暫態模型為:
所述的子模塊電容電壓基頻負序分量的簡化電磁暫態模型為:
所述的子模塊電容電壓基頻零序分量的簡化電磁暫態模型為:
所述的子模塊電容電壓二倍頻正序分量的簡化電磁暫態模型為:
所述的子模塊電容電壓二倍頻負序分量的簡化電磁暫態模型為:
所述的子模塊電容電壓二倍頻零序分量的簡化電磁暫態模型為:
式中,ucd+、ucq+為換流器交流出口正序電壓的dq分量;ucd-、ucq-為換流器交流出口負序電壓的dq分量;isd+、isq+、isd-、isq-為交流相電流基頻正序、基頻負序的dq分量;icird+、icirq+、icird-、icirq-為橋臂環流二倍頻正序、二倍頻負序的dq分量;icirx0、iciry0為橋臂二倍頻零序電流的xy分量;uc_1d+、uc_1q+、uc_1d-、uc_1q-、uc_2d+、uc_2q+、uc_2d-、uc_2q-分別為子模塊電容電壓基頻正序、基頻負序、二倍頻正序、二倍頻負序的dq分量;uc_1x0、uc_1y0、uc_2x0、uc_2y0為子模塊電容電壓基頻零序、二倍頻零序的xy分量;idcb、idcc為b、c相橋臂電流的直流分量;udc為換流器直流側電壓。
所述的a相橋臂電流直流分量的簡化電磁暫態模型為:
所述的橋臂電流基頻正序分量的簡化電磁暫態模型為:
所述的橋臂電流基頻負序分量的簡化電磁暫態模型為:
所述的橋臂電流二倍頻正序分量的簡化電磁暫態模型為:
所述的橋臂電流二倍頻負序分量的簡化電磁暫態模型為:
所述的橋臂電流二倍頻零序分量的簡化電磁暫態模型為:
式中,udc是udc的直流分量;udc_cir0是udc的二倍頻零序分量;usd+、usq+為等值交流系統電壓的正序分量;usd-、usq-為等值交流系統電壓的負序分量;等效電感leq是換流變壓器漏抗lt與1/2的橋臂電抗larm之和,即leq=lt+larm/2,同理,等效電阻req是換流變壓器電阻rt與1/2的橋臂電阻rarm之和,即req=rt+rarm/2。
所述步驟3中相序分離環節的簡化電磁暫態模型為:
其中,
所述的正序電流矢量控制器的控制系統簡化電磁暫態模型為:
其中,
所述的負序電流矢量控制器的控制系統簡化電磁暫態模型為:
鎖相環的簡化電磁暫態模型為:
本發明的有益效果在于:本發明考慮交流側存在負序分量時,在dq旋轉坐標系下基于開關函數建立了包括子模塊電容電壓波動正負零序分量、內部環流正負零序分量的mmc換流站簡化電磁暫態模型,同時考慮相序分離環節、正序及負序電流矢量控制的影響,最后得到了包含交流系統、mmc換流站和控制系統的mmc系統簡化電磁暫態模型。該模型可以方便的研究負序分量以及負序控制在mmc換流站內的動態過程,并為系統參數設計和穩定性分析提供研究基礎。
附圖說明
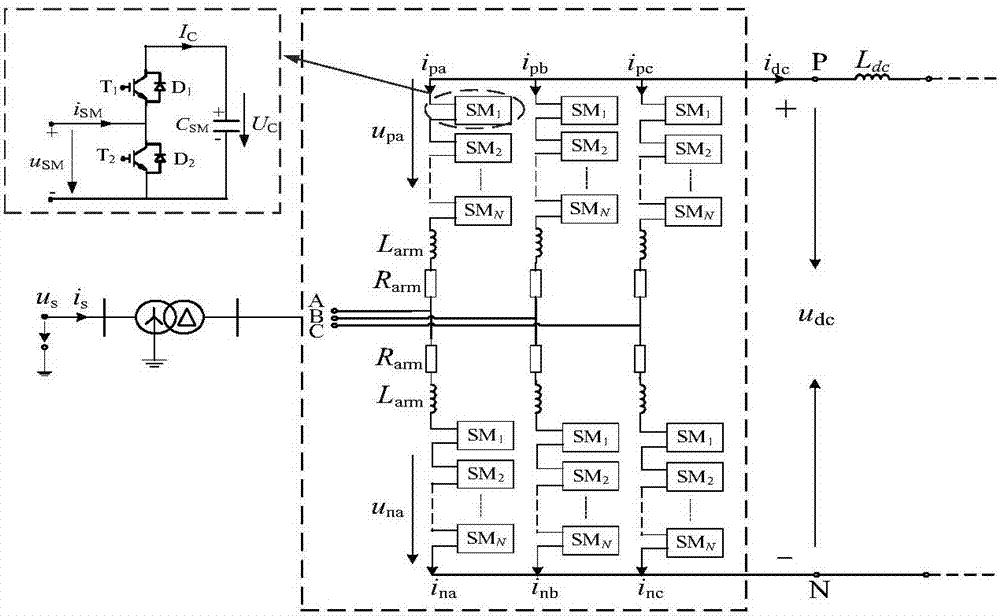
圖1:本發明實施例中mmc系統示意圖;
圖2:本發明實施例中mmc的工作原理圖;
圖3:本發明實施例中mmc站級控制結構圖;
圖4:本發明實施例中mmc系統各部分連接圖;
具體實施方式
下面結合附圖,對實施例作詳細說明。
圖1是本發明的mmc系統示意圖,圖中,mmc換流站通過換流變壓器連接交流系統,換流變壓器采用y/△接線方式,以阻斷交流系統零序分量傳遞到閥側。圖1中:rs、ls為交流系統等值電阻和等值電感;us為等值交流系統的電壓;is為系統側電流;udc1為直流電壓。
圖2是本發明的mmc的工作原理圖。每個換流器有六個橋臂,每個橋臂由n個相同的級聯子模塊(sub-module,sm)、橋臂電抗器larm和橋臂等效電阻rarm串聯而成,在換流器出口配置限流電抗器ldc抑制直流故障電流。圖2中:upj、unj、ipj、inj(j=a,b,c,下同)分別為上、下橋臂電壓和橋臂電流,其中p表示上橋臂,n表示下橋臂;udc為換流器直流出口電壓;idc為直流電流。
為了簡化分析,本實施方式基于以下假設
1)在電容平衡控制的作用下,各橋臂子模塊電容電壓基本完全一致。
2)電平數較高時,只考慮開關函數中的直流分量和基頻分量。
3)忽略高次諧波,考慮橋臂電流和子模塊電容電壓的主要諧波分量。
4)換流器交流出口電壓、交流相電流、橋臂環流、子模塊電容電壓各序分量都是正弦波。
當交流側有負序分量注入時,直流電流在三相橋臂間不再均勻分布,由于mmc上、下橋臂對稱,可以近似認為基頻正序電流和基頻負序電流在上、下橋臂間平分,二倍頻正序和二倍頻負序電流在橋臂間環流,二倍頻零序電流則流向直流側,造成直流電壓的二倍頻波動。由于y/△接線方式的變壓器阻斷了零序電流的通路,所以本發明暫不考慮基頻零序電流分量。忽略三階及以上分量,三相靜止坐標系下考慮負序分量的橋臂電流主要由直流分量、基頻正序、基頻負序、二倍頻正序、二倍頻負序、二倍頻零序分量組成,表達式如下:
式中,ipa、ina分別為a相上、下橋臂電流;idca為a相橋臂電流的直流分量;is+、is-、β1+、β1-分別為交流電流正序、負序分量的幅值和相角;icir+、icir-、icir0、β2+、β2-、β20分別為橋臂二倍頻正序、負序、零序電流的幅值和相角。
忽略三階及以上分量,所述三相靜止坐標系下考慮負序分量的子模塊電容電壓主要由直流分量、基頻正序、基頻負序、基頻零序、二倍頻正序、二倍頻負序、二倍頻零序分量組成,以a相為例表示為:
式中,uc_dca為a相子模塊電容電壓的直流分量,uc1+、uc1-、uc10,uc2+、uc2-、uc20,θ1+、θ1-、θ10,θ2+、θ2-、θ20分別為基頻正序、基頻負序、基頻零序,二倍頻正序、二倍頻負序、二倍頻零序分量的幅值和相角。
開關函數模型如下式所示:
式中,s為平均開關函數,c為子模塊電容,uc為該橋臂子模塊電容電壓,iarm為橋臂電流,uarm為橋臂電壓,n為橋臂的子模塊級聯個數。
采用工程上常用的最近電平逼近調制,以a相為例,上、下橋臂的平均開關函數計算如下
式中,開關函數中的基頻負序分量是由于負序電流矢量控制疊加產生。sx(x=p,n)為上、下橋臂的平均開關函數,當式(4)取“-”號時,表示上橋臂的平均開關函數,“+”號表示下橋臂的平均開關函數,ω為角頻率;m+、m-為正序、負序調制比;ɑ+、ɑ-分別為基頻正負序分量的相角。b相、c相平均開關函數中基頻正序分量的相位依次滯后2π/3,而基頻負序分量依次超前2π/3。
通過橋臂電流和開關函數可得子模塊電容電壓的簡化電磁暫態模型,即將式(4)(1)代入式(3)并分別將等式右側用dq分量(或xy分量)表示:
1)子模塊電容電壓直流分量的簡化電磁暫態模型
2)子模塊電容電壓基頻正序分量的簡化電磁暫態模型
3)子模塊電容電壓基頻負序分量的簡化電磁暫態模型
4)子模塊電容電壓基頻零序分量的簡化電磁暫態模型
5)子模塊電容電壓二倍頻正序分量的簡化電磁暫態模型
6)子模塊電容電壓二倍頻負序分量的簡化電磁暫態模型
7)子模塊電容電壓二倍頻零序分量的簡化電磁暫態模型
式中,ucd+、ucq+為換流器交流出口正序電壓的dq分量;ucd-、ucq-為換流器交流出口負序電壓的dq分量;isd+、isq+、isd-、isq-為交流相電流基頻正序、基頻負序的dq分量;icird+、icirq+、icird-、icirq-為橋臂環流二倍頻正序、二倍頻負序的dq分量;icirx0、iciry0為橋臂二倍頻零序電流的xy分量;uc_1d+、uc_1q+、uc_1d-、uc_1q-、uc_2d+、uc_2q+、uc_2d-、uc_2q-分別為子模塊電容電壓基頻正序、基頻負序、二倍頻正序、二倍頻負序的dq分量;uc_1x0、uc_1y0、uc_2x0、uc_2y0為子模塊電容電壓基頻零序、二倍頻零序的xy分量;idcb、idcc為b、c相橋臂電流的直流分量;udc為換流器直流側電壓。
由子模塊電容電壓和開關函數可得橋臂電壓的表達式,再由kvl得到橋臂電流的動態模型,所以,將式(2)(4)代入式(3)求得橋臂電壓:
式中,由于三相橋臂子模塊電容電壓直流分量不相等,基頻分量中的
以a相為例,式(12)右側的各項表達式為
1)直流電流
由于流過三相橋臂的直流電流不再相等,需要分別表示出三相橋臂電流的直流分量。對j相(j=a,b,c)橋臂與直流側構成的回路,應用kvl得:
其中,udc是udc的直流分量。分別將uarm_dcj的表達式(13)代入式(20),并用dq分量表示,得三相直流電流的簡化電磁暫態模型為(以a相為例):
2)基頻不對稱分量
橋臂電壓中的基頻不對稱分量由三相子模塊電容電壓直流分量不相等引起,使用對稱分量法變成對稱的三序基波分量。同理,將變換后所得的基頻正序分量加入下述3),基頻負序分量加入下述4)中,并一起聯立kvl,使用相應的坐標變換轉換到dq系統。
3)交流電流正序分量
對交流側列kvl得:
式中,us+為等值交流系統電壓的正序分量;等效電感leq是換流變壓器漏抗與1/2的橋臂電抗之和,即leq=lt+larm/2,同理,req=rt+rarm/2。
聯立式(15)和(22)進行基頻正序的坐標變換到dq坐標系下:
4)交流電流負序分量
對交流回路的kvl有:
式中,us-為等值交流系統電壓的負序分量。將式(16)代入(24)并通過基頻負序的坐標變換到dq坐標系下:
5)橋臂環流二倍頻正序分量
由橋臂環流回路的kvl:
將橋臂電壓的二倍頻正序分量表達式(17)代入式(26),并通過二倍頻正序的坐標變換得:
6)橋臂環流二倍頻負序分量
由橋臂環流回路的kvl:
將橋臂電壓二倍頻負序分量(式(18))代入式(28),并通過二倍頻負序坐標變換到dq坐標系下:
7)二倍頻零序分量
二倍頻零序電流流向直流側引起直流電壓的二倍頻波動,由直流側kvl得:
其中,udc_cir0是udc的二倍頻零序分量,又由于
聯立式(19)、(30)與(31)得
直流側通過限流電抗器連接負載。橋臂電流中的直流分量和二倍頻零序分量流向直流側,由圖1、圖2得直流側的簡化電磁暫態模型為:
udc1=rdcidc(34)
idc=idca+idcb+idcc(36)
本發明采用圖3所示的典型的mmc站級控制結構,其中相序分離環節采用多重復系數濾波器法分別提取交流母線處的正負序電流。
1)相序分離環節的簡化電磁暫態模型
如圖3,ω0是正序基波角頻率;ωi是截止頻率;iɑ、iβ是αβ坐標系下的交流母線電流;iɑ+、iβ+、iɑ-、iβ-分別是分離后的交流母線電流正負序分量。相序分離環節基于αβ坐標系,為統一坐標系,需將各變量轉換到dq坐標系下:
其中,
式中,isdm+、isqm+、isdm-、isqm-是相序分離后交流母線正、負序電流的dq分量,θ是pll輸出相角。
2)正序電流矢量控制器的簡化電磁暫態模型
其中,
3)負序電流矢量控制器的簡化電磁暫態模型
4)鎖相環的簡化電磁暫態模型
聯立mmc換流站及交直流側的簡化電磁暫態模型和控制系統的簡化電磁暫態模型,即式(5)—(42),最終得到mmc系統的簡化電磁暫態模型(40階),各部分之間的連接關系如圖4所示。
上述實施例僅為本發明較佳的具體實施方式,但本發明的保護范圍并不局限于此,任何熟悉本技術領域的技術人員在本發明揭露的技術范圍內,可輕易想到的變化或替換,都應涵蓋在本發明的保護范圍之內。因此,本發明的保護范圍應該以權利要求的保護范圍為準。
- 還沒有人留言評論。精彩留言會獲得點贊!