考慮多風場預測誤差時空相關性的儲能容量優化配置方法與流程

本發明涉及一種考慮多風場預測誤差時空相關性的儲能容量優化配置方法。

背景技術：

由于資源與環境問題日益嚴峻，以風能為首的新能源開發和利用在全球范圍內受到廣泛關注，并持續保持快速發展水平。根據全球風能理事會(gwec)發布的全球風能數據，截止到2015年，全球風電裝機容量達到433gw且2016年又將增加60gw。我國風電裝機容量截止2015年達到145.4gw，比2014年增長了21.2％。然而，由于風電機組出力的不確定性和波動性，風電大規模并網必將對電力系統安全、可靠、穩定和經濟運行帶來巨大挑戰。

隨著儲能技術的發展，安裝儲能系統(ess)被看作減小風電機組隨機性和不確定性影響的有效方法。然而，由于目前多數類型的儲能價格依然相對較為昂貴，優化儲能容量是當前儲能應用中的一個關鍵性問題。目前，關于風電場儲能的優化配置問題，學者們進行了大量的有益的研究工作。

但是，現有的研究僅針對單一風場，并未考慮多風場之間的相關關系。而距離較近的風電場之間的風電功率預測誤差具有非常強的相關性，這一特性將直接影響風電功率的總體波動特性、儲能配置結果的經濟性與有效性。

預測誤差的時空相關性分析時風儲系統研究的重要基礎，準確分析風場間時空相關性對于確定合理的儲能容量十分重要，因此有必要對考慮預測誤差特性和時空相關性的儲能優化配置進行進一步研究，尤其是現有的考慮誤差分布的儲能容量優化研究存在以下問題：

(a)并未同時考慮風場之間的時空相關性；

(b)利用線性方法擬合預測誤差無法保持數據的原始分布特性，用于規劃儲能會錯誤估計所需容量；

(c)均未提到預測誤差時間相關性和空間相關性如何影響風儲系統容量配置和成本效益。

技術實現要素：

本發明為了解決上述問題，提出了一種考慮多風場預測誤差時空相關性的儲能容量優化配置方法，本發明基于多場景分析方法，以儲能系統綜合成本效益最優為目標，建立考慮多風場間風電功率預測誤差時空相關性的儲能容量優化模型。

為了實現上述目的，本發明采用如下技術方案：

一種考慮多風場預測誤差時空相關性的儲能容量優化配置方法，通過對比分析參數和非參數兩種方法對預測誤差的擬合效果，選取擬合精度最高的kde方法進行誤差擬合；采用copula理論的多風電場預測誤差時空相關性建模方法，根據多風場間實際空間相關關系，得到多風場預測誤差聯合分布函數，利用kde方法擬合預測誤差的邊緣分布函數；基于多場景分析方法，以儲能系統投資成本和運行成本最小為目標，建立考慮多風場間預測誤差時空相關性的儲能容量優化模型。

進一步的，所述預測誤差為功率實際值減去預測值，且位于[-1,1]之間的數據。

進一步的，分別利用正態分布、t分布和kde方法擬合預測誤差來進行風功率預測誤差分析，確定最優擬合方法。

進一步的，進行多風電場預測誤差時空相關性分析，風電場之間的距離越近，其預測誤差線性相關系數越大，時空相關性越強。

進一步的，采用copula理論的多風電場預測誤差時空相關性建模的具體過程包括：

(1)生成n風場功率預測誤差矩陣，假設每風場有t個時間段，每個時間段內有t個觀測值，構建預測誤差矩陣；

(2)利用kde擬合方法計算預測誤差邊緣分布；

(3)利用最大似然估計法對normal/tcopula函數參數進行估計，其中normalcopula函數參數為t×t秩相關矩陣ρ，tcopula函數參數為t×t秩相關矩陣和自由度；

(4)利用normal/tcopula方程計算得到多風場預測誤差聯合分布函數。

進一步的，根據構建的normal/tcopula生成的聯合分布函數進行反變換，生成預測誤差場景。

進一步的，利用向后縮減技術對原始場景進行縮減，尋找最接近原始系統的場景，計算確定的每個場景的棄風能量和損失能量。

進一步的，蓄電池儲能容量優化的目標為補償風電功率預測誤差和使儲能系統投資成本與風儲系統運行成本最小以實現綜合效益最優。

進一步的，利用折中方法考慮投資成本和運行成本間的對立關系以實現風儲系統的優化運行，運行成本包括棄風成本和損失成本，兩者隨額定容量和充放電功率的變化而變化。

進一步的，蓄電池儲能容量優化的約束條件包括蓄電池約束和輸出功率約束，蓄電池約束又包括充電功率約束和放電功率約束。

與現有技術相比，本發明的有益效果為：

(1)本發明利用kde擬合各時間段預測誤差的概率分布函數和多元聯合分布函數的邊緣分布函數，擬合效果最好；

(2)本發明建立基于copula函數的預測誤差時空相關性模型，得到多風場預測誤差的聯合分布函數，該聯合分布包含了各風場的時間相關性和風場間的空間相關性；

(3)本發明構建了考慮風電場時空相關性的儲能容量規劃模型。該模型也考慮了投資成本與運行成本間的對立關系，模型目標是實現風儲系統的最優綜合效益；

(4)算例計算結果證明了對bess容量進行優化可以有效補償風電功率預測誤差以及減小預測方法局限的影響；通過對計算結果進行對比分析，預測誤差時空相關性對于bess配置有顯著影響，風電場間的空間相關性越強，風儲系統綜合成本效益越好，對風電功率預測誤差的補償效果越好。

附圖說明

構成本申請的一部分的說明書附圖用來提供對本申請的進一步理解，本申請的示意性實施例及其說明用于解釋本申請，并不構成對本申請的不當限定。

圖1是本發明實施例中四個風電場地理位置分布圖；

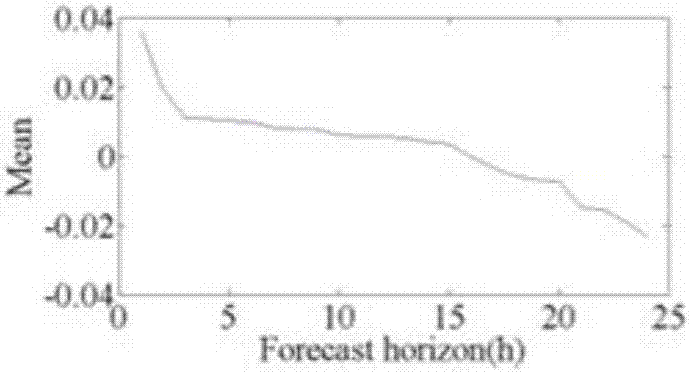
圖2(a)-圖2(d)是本發明a風場24小時預測誤差均值、方差、偏度與峰度計算結果圖；

圖3(a)-圖3(d)是本發明a風場分別提前1小時、提前7小時、提前8小時和提前24小時預測誤差概率密度分布直方圖和利用normal分布，t分布以及kde方法得到的擬合概率密度函數；

圖4(a)-圖4(d)是本發明a風場分別提前1小時、提前7小時、提前8小時和提前24小時預測誤差擬合分布函數與經驗分布函數qq圖；

圖5是本發明預測誤差的線性相關結構圖；

圖6是本發明場景生成步驟圖；

圖7是本發明a風場第一天功率觀測值、預測值和置信區間示意圖；

圖8(a)-圖8(d)是本發明a風場第一天預測誤差場景縮減結果，其中，(a)不考慮時空相關性；(b)時空相關性最強；(c)時間相關性最強空間相關性較強，(d)時間相關性最強空間相關性最弱；

圖9是本發明a風場原始預測誤差曲線和經過不同時空相關性的儲能補償后的預測誤差曲線圖。

具體實施方式：

下面結合附圖與實施例對本發明作進一步說明。

應該指出，以下詳細說明都是例示性的，旨在對本申請提供進一步的說明。除非另有指明，本發明使用的所有技術和科學術語具有與本申請所屬技術領域的普通技術人員通常理解的相同含義。

需要注意的是，這里所使用的術語僅是為了描述具體實施方式，而非意圖限制根據本申請的示例性實施方式。如在這里所使用的，除非上下文另外明確指出，否則單數形式也意圖包括復數形式，此外，還應當理解的是，當在本說明書中使用術語“包含”和/或“包括”時，其指明存在特征、步驟、操作、器件、組件和/或它們的組合。

正如背景技術所介紹的，現有技術中存在并未同時考慮風場之間的時空相關性以及利用線性方法擬合預測誤差無法保持數據的原始分布特性，用于規劃儲能會錯誤估計所需容量的不足，為了解決如上的技術問題，本申請提出了一種考慮多風場預測誤差時空相關性的儲能容量優化配置方法。

主要貢獻如下：

1)提出了基于copula函數的預測誤差高維建模方法，建立多風場預測誤差的聯合分布函數，該聯合分布包含了各風場的時間相關性和風場間的空間相關性。

2)基于預測誤差的聯合分布，本發明考慮儲能系統的投資成本與運行成本兩者間對立關系，基于多場景技術，對儲能容量進行優化配置，使風儲系統的綜合效益達到最優。

3)通過對比分析預測誤差時空相關性對風電場儲能配置有顯著影響，風電場間的空間相關性越強，風儲系統綜合成本效益越好，對風電功率預測誤差的補償效果越好。

本申請的一種典型的實施方式中，所用數據來自冀北地區的四個風電場，其地理位置分布如圖1所示，四個數據集合分別為a、b、c和d。每個數據集包含2013年全年數據，并根據各自裝機容量進行歸一化處理。本發明采用文獻liangz,liangj,wangc,etal.short-termwindpowercombinedforecastingbasedonerrorforecastcorrection[j].energyconversionandmanagement,2016,119:215-226提出的風電功率方法預測風功率得到8688個預測功率數據和相應的預測誤差。預測誤差等于功率實際值減去預測值，且位于[-1,1]之間。

圖2為a風場24小時預測誤差的均值、方差、偏度與峰度計算結果，bcd三風場的計算結果圖如附錄圖1—圖3所示。由圖2(a)-圖2(d)可知，圖2(a)各時段預測誤差的均值均不為零；圖2(b)隨著預測區間增大，預測誤差的方差逐漸減小；圖2(c)預測誤差大于2h后的偏度系數均小于零，表示對應時間段的預測誤差分布為左偏，且隨著預測區間的增大，偏度系數絕對值逐漸增大，表示拖尾越長；圖2(d)峰度隨著預測區間的增大而減小，表示誤差分布形態逐漸變緩，且峰度系數均大于3，表示誤差分布有明顯的厚尾特征。因此，a風場24小時預測誤差形態呈現尖峰、厚尾、拖尾的特征，為了更加清晰地分析預測誤差的特征，本發明利用不同擬合方法計算并繪制預測誤差的概率分布，如圖3(a)-圖3(d)所示，為a多風場提前1小時、7小時、8小時和24小時的預測誤差概率密度分布直方圖和利用正態分布、t分布和kde方法擬合的概率密度函數對比圖，可知，隨著預測區間的增大，(a)預測誤差概率密度分布曲線逐漸由凸變平；(b)基于正態分布的概率密度函數與預測誤差的經驗概率密度函數之間的區別逐漸增大，而基于kde的概率密度分布與經驗概率密度函數之間無明顯差別；(e)當預測區間大于7小時時，t分布由于最大似然估計發散而無法擬合預測誤差；(f)預測誤差的概率密度分布的尾部逐漸變厚。

qq圖是用來擬合分布函數與經驗分布函數之間的距離，若兩者都重合或者接近于45°直線，說明擬合度較高。圖4(a)-圖4(d)為a風場提前1小時、7小時、8小時和24小時預測誤差擬合分布函數與經驗分布函數qq圖，可以看出kde擬合分布函數最接近45°直線，擬合效果最好。基于以上分析，本發明選用kde方法擬合copula函數的邊緣分布函數。

預測誤差線性相關結構如圖5所示。圖5表示相鄰時間區間的預測誤差具有很強的時間相關性。結合圖1的四風場地理位置分布，ab兩風場距離最小，其最大線性相關系數為0.6425，因此ab兩風場預測誤差時空相關性最強。ac兩風場的最大線性相關系數為0.4338，其距離大于ab間距離。ad兩風場相距最遠，其最大線性相關系數為0.06536，幾乎沒有相關性。因此，風電場距離越近，其預測誤差線性相關系數越大，時空相關性越強。

copula函數提供了一種構造不同獨立變量的聯合分布的方法，該分布包含了隨機變量的相關關系并且能夠捕捉其非線性相關關系。

數學上，sklar定理強調任何多元聯合分布可以寫成單變量的邊緣分布和一個描述變量間相關結構的copula函數。假設x1,x2,…xn為隨機變量，其邊緣分布函數為f1(x1),f2(x2),…,ft(xt)，且均遵循以下均勻分布：

f1(x1)～u(0,1),f2(x2)～u(0,1),…,fn(xn)～u(0,1)(2)

根據sklar定理，f1(x1),f2(x2),…,ft(xt)的聯合分布為：

f(x1,x2,…,xt)＝c(f1(x1),f2(x2),…,ft(xt))(3)

其中c即為copula函數。

由于normal/tcopula可以用于多元建模，允許任何邊緣分布和正定矩陣，因此本發明利用normal/tcopula函數建立日前預測誤差多元分布函數。normal/tcopula函數如式(4)(5)所示：

f(x1,x2,…,xt；ρ)＝c(f1(x1),f2(x2),…,ft(xt)；ρ)

＝φρ(φ^-1(f1(x1)),φ^-1(f2(x2)),…,φ^-1(ft(xt)))(4)

f(x1,x2,…,xt；ρ,k)＝c(f1(x1),f2(x2),…,ft(xt)；ρ,k)

＝tρ,k(tk^-1(f1(x1)),tk^-1(f2(x2)),…,tk^-1(ft(xt)))(5)

其中，

φ^-1標準正態分布的分布函數的反函數

φρ標準正態分布的分布函數

ρ對稱正定矩陣

t分布的分布函數的反函數

tρ,kt分布的分布函數

k自由度

利用copula理論的多風場風電功率預測誤差建模步驟

基于以上分析，n風場預測誤差的高維建模步驟如下。

1)生成n風場功率預測誤差矩陣。假設每風場有t個時間段，每個時間段內有t個觀測值。則預測誤差矩陣可由式(6)表示。

其中為第n個風電場t時間段第t個預測誤差值。

2)利用kde擬合方法計算預測誤差邊緣分布。擬合結果形式如式(7)所示。

3)利用最大似然估計法對normal/tcopula函數參數進行估計。normalcopula函數參數為t×t秩相關矩陣ρ，tcopula函數參數為t×t秩相關矩陣ρ和自由度k。

4)利用normal/tcopula方程計算得到多風場預測誤差聯合分布函數(jcdf)。

在由normal/tcopula生成的聯合分布函數的基礎上，可生成預測誤差場景。圖6為多場景的生成步驟，其中ppre為風電功率預測值。根據圖6可生成m-t維風電功率預測誤差場景。

為減小模型規模提高運算效率，有必要對中生成的場景進行縮減。本發明利用向后縮減技術對原始場景進行縮減。以尋找最接近原始系統的場景。

蓄電池儲能容量優化的目的為：(a)補償風電功率預測誤差；(b)使儲能系統投資成本與風儲系統運行成本最小以實現綜合效益最優。本發明利用折中方法考慮投資成本和運行成本間的對立關系以實現風儲系統的優化運行。運行成本包括棄風成本和損失成本，兩者隨額定容量和充放電功率的變化而變化。為更加有效的分析風電功率預測誤差的時空相關性對蓄電池儲能容量優化配置的影響，本發明分析當地的風況并選取特征最為明顯的月份作為研究對象。

縮減場景數之后，每個場景的棄風能量和損失能量如式(8)(9)所示。

式(8)與(9)中

ci,bessn＝max(ci,bess(t))-min(ci,bess(t))(15)

pi,bessn＝max(pi,besscen,|pi,bessden|)(16)

對于第i個場景，其中

si,su1(t)布爾量，用于描述由充電功率限制產生的棄風能量

si,su2(t)布爾量，用于描述由蓄電池額定容量限制產生的棄風能量

si,sh1(t)布爾量，用于描述由放電功率限制產生的損失能量

si,sh1(t)布爾量，用于描述由蓄電池最小容量限制產生的損失能量

t時間尺度

pi(t)t時刻的風電功率

參考輸出功率區間

pi,besscen額定充電功率

pi,ce(t)t時刻的充電功率

pi,bessden額定放電功率

pi,de(t)t時刻的放電功率

ci,bess(t)t時刻的荷電狀態

ci,bessn額定容量

dod放電深度

xi,c(t)0-1變量，表示t時刻的充電功率

xi,d(t)0-1變量，表示t時刻的放電功率

本發明釩電池為例進行具體分析說明，其相關參數如表1所示。

表1釩電池參數

儲能配置的目標函數是風儲系統的成本最小。每個場景下的目標函數為：

minf＝ksuρ1wi,su+kshρ2wi,sh

+kin(ρcci.bessn+ρppi.bessn+rs)(17)

對于第i個場景，其中

ρ1棄風能量對應單價

ρ2損失能量對應單價

ρc額定容量對應單價

ρp額定功率對應單價

rs儲能系統安裝成本

ksu棄風能量成本系數

ksh損失能量成本系數

kin投資成本系數

約束條件包括蓄電池約束和輸出功率約束：

充電功率約束：

放電功率約束：

輸出功率約束：

分別計算m個場景的優化結果，其額定容量和充放電功率如下：

其中pi為第i個場景的概率。

為驗證提出的儲能配置模型，在求出式(21)—式(23)額定容量和充放電功率的基礎上，將其作為b中模型的已知量，利用風電功率實測數據作為模型的輸入量(即上述模型中的pi(t))，計算棄風成本、損失成本和最優綜合成本。

為分析預測誤差時空相關性對風儲系統綜合成本效益的影響以及證明上述方法的有效性和可行性，本發明對風電場30天數據，設計以下4個算例為a風電場配置儲能：(a)不考慮預測誤差的時空相關性；(b)考慮ab兩風場間預測誤差時空相關性最強的情況；(c)考慮ac兩風場間預測誤差較強空間相關性以及風場自身的時間相關性的情況；(d)考慮ad兩風場間預測誤差最弱空間相關性和風場自身的時間相關性的情況。根據第四部分提出的蓄電池儲能優化模型，需要首先確定輸出功率參考值。假設輸出功率參考值為一個區間，該區間由相應的預測誤差分布。圖7為a風場第一天的參考功率，由圖7可以看出輸出功率的范圍隨著預測區間增加而增大。

根據基于normal/tcopula得到的多元聯合分布函數，可分別得到每個算例中各個時間段的1000個場景，并利用向后縮減法將1000個場景縮減為10個。

圖8(a)-圖8(d)為場景縮減后的10個場景：圖8(a)不考慮時空相關性；圖8(b)時空相關性最強；圖8(c)時間相關性最強空間相關性較強，圖8(d)時間相關性最強空間相關性最弱。可以看出，所有場景均隨預測區間的增大而呈現發散趨勢。對比四個算例的場景縮減圖，不考慮時空相關性時的場景波動最為劇烈，隨著空間相關性的增強，場景波動隨之減弱。

本發明利用gams平臺對第三部分提出的優化模型進行計算。充電功率、放電功率和額定容量計算結果如表3所示。由表3可以看出：(a)與其他三種算例相比，不考慮預測誤差時空相關性時額定充電功率和額定放電功率絕對值最大；(b)考慮時空相關性時，額定容量比不考慮時空相關性的算例1大得多；(c)比較算例2、算例3和算例4，額定充電功率和額定放電功率的絕對值隨著空間相關性的減弱而增大；(d)考慮時空相關性時，額定容量隨著空間相關性的減弱而減小；(e)基于tcopula計算得到的額定充電功率和額定放電功率的絕對值大于由normalcopula求得的結果；(f)由tcopula計算得到的額定容量比基于normalcopula得到的要小。

表3儲能優化模型額定充放電功率和額定容量優化計算結果

表4為運行成本和最優綜合成本。由表4可以看出，(a)算例1基于kde計算得到的運行成本和綜合成本最大；(b)考慮預測誤差時空相關性的算例中，運行成本與綜合成本均隨著空間相關性的減弱而增大；(c)對于算例2、算例3和算例4，基于tcopula的計算結果均小于由normalcopula計算得到的結果。

表4運行成本和綜合成本計算結果

圖9為原始預測誤差曲線和經過儲能補償的預測誤差曲線。由上圖可明顯看出為風電場配置儲能可以有效補償預測誤差，且風電場間預測誤差的空間相關性越強，補償效果越好。

總之，若不考慮風電功率短期預測誤差的時空相關性，則會導致額定容量被高估、充放電功率被低估。若考慮預測誤差時空相關性，不同空間相關性的綜合成本效益差異明顯，風電場間的空間相關性越強，風儲系統綜合成本效益越好，對風電功率預測誤差的補償效果越好。

以上所述僅為本申請的優選實施例而已，并不用于限制本申請，對于本領域的技術人員來說，本申請可以有各種更改和變化。凡在本申請的精神和原則之內，所作的任何修改、等同替換、改進等，均應包含在本申請的保護范圍之內。

上述雖然結合附圖對本發明的具體實施方式進行了描述，但并非對本發明保護范圍的限制，所屬領域技術人員應該明白，在本發明的技術方案的基礎上，本領域技術人員不需要付出創造性勞動即可做出的各種修改或變形仍在本發明的保護范圍以內。