基于二層規劃考慮電壓穩定性的交直流系統無功優化方法與流程
本發明涉及電力系統無功優化領域,尤其是涉及一種考慮全面、可靠性高、邏輯結構清晰、實用合理的考慮電壓穩定性的交直流系統無功優化方法。
背景技術:
近年來,我國大力推進發展特高壓交流、直流系統。截止到2016年末,我國已擁有了世界上唯一同時運行特高壓交、直流的電網。相比傳統輸電系統,特高壓直流輸電三個方面優勢突出:大容量長距離輸送電能;快速調節直流線路功率,改善系統運行的穩定性;聯接兩個不同步或頻率不同的電網。這些優點使得直流輸電受到愈來愈多的重視,電網所占比例不斷增大,交直流混聯的電網運行方式已成為我國電網發展的典型特征。
直流系統的換流器在運行的過程中,從交流系統吸收大量無功功率,在直流換流站附近需要近安裝無功補償設備提供無功功率以保證充足的無功功率。此外,由于直流輸電輸入大量電能,代替了大量本地火電機組,使得電網電壓支撐能力下降,電壓穩定日益凸顯。如何處理好交直流混合電力系統無功優化,同時確保系統的電壓穩定,是目前所需要應對的新問題。
二層規劃,是多層規劃的一種特殊形式。將具有兩個層次的系統問題進行綜合考慮,上層問題和下層問題都有各自的目標函數和約束條件,上層決策變量通過自身的決策變量指導下層決策,下層決策問題以上層決策變量作為參數,在自身可行域范圍內進行決策,并將其最優值或最優解反饋至上層,上層模型再次進行優化求解,如此反復求解,從而實現上下層的相互聯系和相互制約。
技術實現要素:
本發明的目的是為了克服上述現有技術存在的缺陷,而提供一種基于二層規劃方法考慮電壓穩定裕度的交直流系統無功優化方法。
本發明的目的可以通過以下技術方案來實現:
一種基于二層規劃方法考慮電壓穩定裕度的交直流系統無功優化方法,用以尋求滿足經濟性和可靠性的無功優化方案:
采用二層規劃方法建立交直流系統無功優化二層模型,包括上層模型和下層模型,并分別確定上層模型和下層模型的目標函數和約束條件;
采用遺傳算法和原始-對偶內點法的混合算法求解上層數學模型獲取最優的無功優化方案;
采用了連續潮流算法和遺傳算法的混合優化算法求解下層數學模型求解交直流系統的最大電壓穩定裕度。
其中,所述的上層模型以系統有功網損最小作為目標函數,以正常運行狀態下的潮流等式約束、以及一系列不等式約束條件構成。
所述的下層模型以系統的電壓穩定裕度最大為目標函數,以潮流等式約束、不等式約束為約束條件。
與現有技術相比,本發明具有以下優點:
本發明中提出的基于二層規劃方法,構建了交直流混合系統無功優化數學模型。利用二層規劃方法構建考慮電壓穩定裕度的交直流系統無功優化二層優化數學模型,在對系統進行無功優化的同時,使得節點電壓分布得到了改善,有效確保電力系統的電壓在合理的范圍內。
本發明的上層模型以系統有功網絡損耗最小為目標函數,下層模型以系統節點的電壓穩定裕度最大為目標函數,尋求滿足經濟性和可靠性的無功優化方案。上層模型算法采用了跟蹤中心軌跡內點法和遺傳算法(GA)相結合的混合算法,以彌補內點法和遺傳算法各自的缺點,能有效處理交直流系統中存在的大量連續變量和離散變量,同時保證計算的收斂性。下層模型采用了連續潮流算法和遺傳算法的混合優化算法求解系統的電壓裕度。數學模型和優化方法具有準確性、有效性,以及較快的收斂速度。
附圖說明
圖1為本發明所述交直流系統無功優化方法中混合算法的流程圖。
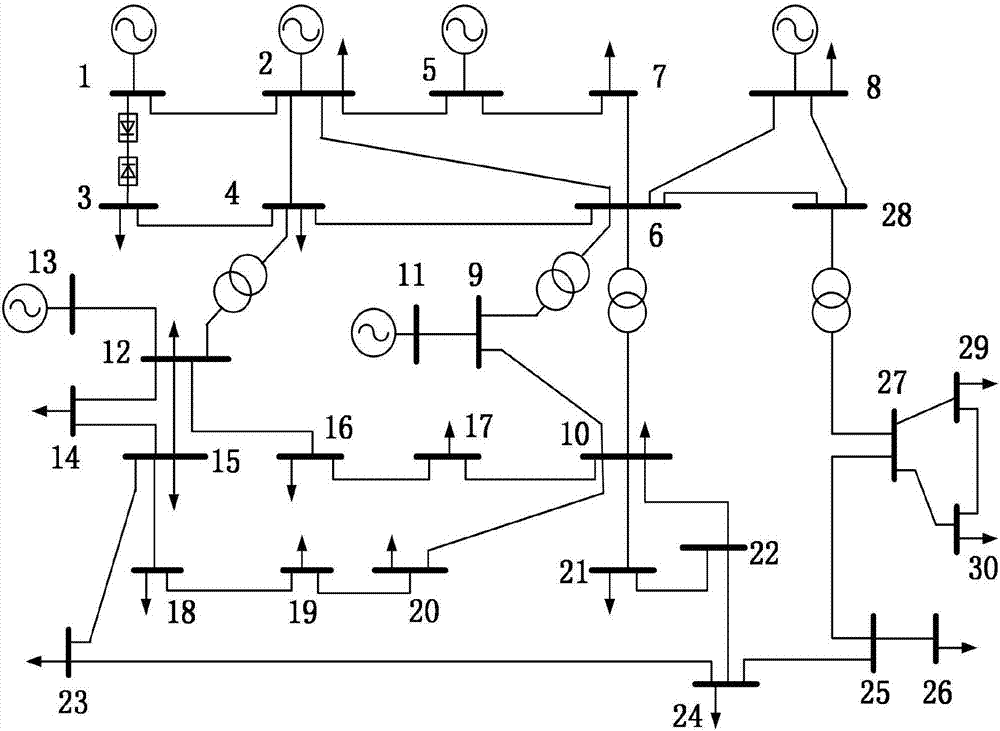
圖2為使用本發明優化的一個實施例的結構圖。
具體實施方式
下面結合附圖和具體實施例對本發明進行詳細說明。
根據二層規劃理論,建立考慮電壓穩定裕度的交直流系統無功優化數學模型;上層模型是以系統有功網損最小作為目標函數,以正常運行狀態下的潮流等式約束、以及一系列不等式約束條件構成,根據模型特點上層采用了遺傳算法和原始-對偶內點法結合的混合優化算法;下層模型以系統的電壓穩定裕度最大為目標函數,以潮流等式約束、不等式約束為約束條件構成,采用遺傳算法和連續潮流算法相結合的混合算法。通過上下層的交替迭代求解模型得到最優方案。
上層模型的目標函數為:
正常運行狀態下的潮流等式約束:
不等式約束條件約束為:
Ui,min≤Ui≤Ui,max i=1,...,N
QCi,min≤QCi≤QCi,max i=1,...,NC
PGi,min≤PGi≤PGi,max i=1,...,NG
QGi,min≤QGi≤QGi,max i=1,...,NG
式中:Ploss為系統的有功網絡損耗;nL為系統中的支路總數;Gk(i,j)為系統第k條支路的電導;Ui、Uj分別為系統節點i和j的節點電壓;θij為節點i和j之間的相角差;Rd為直流線路電阻;Id為直流線路電流;Gij、Bij為節點i和j之間線路的電導和電納;PGi、PDi分別為節點i發電機有功出力和負荷有功,QGi、QDi、QCi分別為節點i發電機無功出力、負荷無功以及無功補償功率;Pti(DC)、Qti(DC)分別為交流系統輸入節點i處換流器的有功、無功功率;s為直流系統系數,節點表示交流節點時s=0,當節點連接整流器時s=1,當節點連接逆變器時s=-1,Ui,max、Ui,min和QCi,max、QCi,min分別是節點電壓上下限和補償電容組上下限,Nc為電容器組數;PGi,max、PGi,min和QGi,max、QGi,min分別發電機有功、無功出力上下限。
所述的下層模型以系統的電壓穩定裕度最大為目標函數,以潮流等式約束、不等式約束為約束條件,則有:
下層模型的目標函數為:
max λ
潮流等式約束:
PGi=PGi(0)(1+λkGi)
不等式約束條件:
KTi,min≤KTi≤KTi,max i=1,...,NT
式中λ為系統電壓穩定裕度,PDi(0)、QDi(0)為節點i的基本負荷,kDi、kGi分別表示隨著λ變化,負荷變化率、發電機出力變化的乘子,S為規定λ適當比例的視在功率;為節點i負荷變化的功率因數角;KTi、KTi,max、KTi,min分別為有載調壓變壓器的變比及上下限,NT為變壓器臺數。
圖1為本實施例混合算法的流程圖。如圖2所示的實施例中,模擬的電力系統采用以標準的IEEE30節點系統為基礎改進的交直流混合系統,該系統現有30個節點、41條線路,其中支路1-3為直流線路,節點1為逆變端,節點3為整流端。
本實施例中上層求解無功優化采用遺傳算法和原始-對偶內點法結合的混合優化算法,下層求解系統的最大負荷裕度采用遺傳算法和連續潮流算法相結合的混合算法。具體步驟為:
第一步:生成初始種群:對上層模型交流系統離散變量:對發電機無功出力、無功補償電容器組數,以及直流系統決策變量編碼,形成初始種群P1;
第二步:計算個體適應度V1:利用內點法和遺傳算法的混合算法求解種群P1中個體的適應度V1(交流系統和直流系統之間采用交替迭代法求解),并根據個體適應值進行排序;
第三步:依次執行采用精英策略的選擇操作、染色體多點交叉操作、染色體多點變異操作,生成新的子代;
第四步:求得上層最優解F1,將相應的上層交流離散變量及直流控制變量作為下層初始系統參數代入下層數學模型;
第五步:下層優化過程以系統變壓器的變比作為優化變量進行編碼,生成初始種群P2;
第六步:利用連續潮流算法和遺傳算法相結合的混合算法求解交直流系統的電壓穩定裕度,計算個體適應度V2,并排序;
第七步:采取與第三步相同的操作,獲得子代種群;
第八步:求得下層最優解F2及相應的變壓器的變比,轉至第一步的操作,將下層求得變壓器變比代入上層模型作為上層初始參數;
第九步:重復循環以上操作:若經多次上下層優化后系統的有功網損偏差滿足要求則結束計算,否則不收斂。
盡管本發明的內容已經通過上述優選實施例作了詳細介紹,但應當認識到上述的描述不應被認為是對本發明的限制。在本領域技術人員閱讀了上述內容后,對于本發明的多種修改和替代都將是顯而易見的。因此,本發明的保護范圍應由所附的權利要求來限定。
- 還沒有人留言評論。精彩留言會獲得點贊!