MEES中永磁同步電機反推自適應直接轉矩控制方法與流程

本發明屬于電機技術領域，涉及以機械彈性儲能箱為負載的永磁同步電機的控制方法，由其是一種MEES中永磁同步電機反推自適應直接轉矩控制方法。

背景技術：

機械彈性儲能裝置的儲能元件為機械彈性儲能箱，其內部結構為蝸卷彈簧的并列。通過永磁同步電機(Permanent Magnet Synchronous Motor，PMSM)的驅動實現電能到機械彈性勢能的轉換與存儲。在儲能過程中儲能箱的轉矩和轉動慣量連續時變，特別是儲能箱反向作用力矩隨儲能過程的進行而逐漸變大，如果電機輸出轉矩不能快速匹配，可能導致儲能箱帶著電機反轉，損毀電機。同時轉動慣量的時變特性可能造成電機轉速的抖震，影響儲能箱的機械性能和破壞儲能過程的平穩性。蝸卷彈簧作為大型剛性機械部件，需要一種自治性較強的控制系統，保證儲能時永磁同步電動機在低速下平穩運行。

技術實現要素：

本發明的目的在于針對現有的電機控制方案對時變負載控制性能的不足，提供一種反推自適應直接轉矩控制方法,實現儲能控制系統的平穩運行。

本發明所述問題是以下述技術方案實現的：

一種MEES中永磁同步電機反推自適應直接轉矩控制方法，所述方法首先建立由機械彈性儲能箱、PMSM、變頻器依次連接而成的機械彈性儲能系統的數學模型；然后設計遺忘因子遞推最小二乘辨識算法辨識儲能箱轉矩和轉動慣量，實時更新控制對象參數，并結合其辨識結果設計速度、轉矩、磁鏈反推控制器，同時設計自適應控制方法，消除辨識誤差對控制系統的影響，保證儲能系統能在低速下平穩運行。

上述為帶機械彈性儲能裝置的PMSM反推自適應直接轉矩控制方法，所述方法包括以下步驟：

a.根據PMSM的實際運行參數，建立機械彈性儲能裝置的數學模型：

T＝T₀+cδ＝T₀+cωt

其中：T為蝸簧箱機械轉矩，J為蝸簧箱轉動慣量，T₀為蝸簧箱初始轉矩，ω、δ分別為蝸簧芯軸的轉速和轉過的角度，c為蝸簧轉矩系數，E、l、b和h分別為蝸簧的材料彈性模量、長度、寬度和厚度，t為時間，J_e為蝸簧完全釋放時的轉動慣量，n為蝸簧箱總的儲能圈數，u_α、u_β為定子α、β軸電壓，i_α、i_β為定子電流α、β軸分量，L為定子電感，ψ_α、ψ_β為定子磁鏈α、β軸分量，ψ為定子磁鏈，R為定子相電阻，n_p為轉子極對數，ω為轉子機械角速度，T_e為電磁轉矩，B_m為粘滯阻尼系數，E_α、E_β為電機的反電動勢α、β軸分量。

b.蝸簧箱轉矩和轉動慣量同時辨識：

Δω(k)＝ω(k)-ω(k-1)

式中，T為蝸簧箱機械轉矩，J為蝸簧箱轉動慣量，n_p為轉子極對數，是θ的估計值，K和P分別為增益矩陣和協方差矩陣，ψ_α、ψ_β為定子磁鏈α、β軸分量，i_α、i_β為定子電流α、β軸分量，λ是遺忘因子，和蝸簧箱轉動慣量和轉矩的辨識值，T_s為采樣周期，k為采樣點，和表示和的辨識誤差，I為單位矩陣。

c.反推自適應直接轉矩控制器設計

e_θ＝θ-θ_ref

e_ω＝ω-ω_ref

e_T＝T-T_ref

e_ψ＝ψ-ψ_ref

E_α＝-ωψ_fsinθ

E_β＝ωψ_fcosθ

式中，θ_ref、ω_ref、T_ref和ψ_ref分別為θ、ω、T和ψ的參考值，θ、ω、T和ψ分別為儲能箱工作圈數，電機轉子角速度，儲能箱轉矩和轉子磁鏈，e_θ、e_ω、e_T和e_ψ為誤差變量，分別為θ_ref的一、二、三階導數，為的導數，k_θ、k_ω、k_T、k_ψ為正的控制增益，L為定子電感，ψ_α、ψ_β為定子磁鏈α、β軸分量，i_α、i_β為定子電流α、β軸分量，E_α、E_β為電機的反電動勢α、β軸分量，ψ_f為轉子永磁磁鏈，T_e為電磁轉矩，為u_α、u_β的參考值。

c.將控制電壓和輸入到PMSM數學模型，實現對PMSM的控制。

本發明的優點和積極效果：

1、本發明充分利用了直接轉矩控制控制的優點，并引入了辨識和反推自適應控制算法，使控制系統具有更好的動態性能。

2、本發明針對蝸簧儲能特點，設計了遺忘因子最小二乘法遞推辨識算法同時辨識轉矩和轉動慣量；并且基于辨識結果設計反推自適應直接轉矩控制器。試驗結果表明，本發明實現了永磁同步電機的高精度控制，保證機械彈性儲能系統平穩高效的儲能。

附圖說明

下面結合附圖對本發明作進一步說明。

圖1是機械彈性儲能機組儲能部分系統模型；

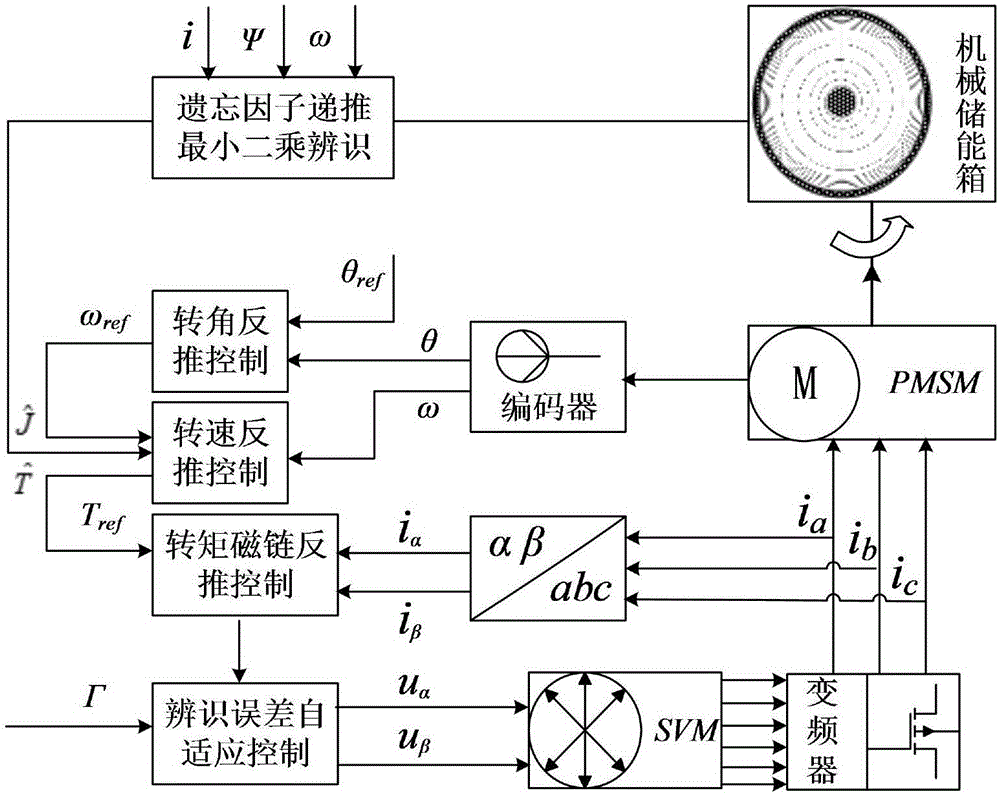
圖2是反推自適應直接轉矩控制實現框圖；

圖3(a)是儲能箱轉矩辨識效果曲線圖；

圖3(b)是儲能箱轉動慣量辨識效果曲線圖

圖4是儲能箱工作圈數曲線圖；

圖5是電機轉速變化曲線圖；

圖6是轉矩跟蹤變化曲線圖；

圖7是電機相電流變化曲線圖；

文中各符號為：T為蝸簧箱機械轉矩，J為蝸簧箱轉動慣量，T₀為蝸簧儲能時的初始轉矩，δ儲能箱轉過的角度，c為蝸簧轉矩系數，E、L、b和h分別為儲能蝸簧的材料彈性模量、長度、寬度和厚度，t為時間，J_e為蝸簧完全釋放時的轉動慣量，n為蝸簧總的儲能圈數，u_α、u_β為定子α、β軸電壓，i_α、i_β為定子α、β軸電流，L為定子電感，ψ_α、ψ_β為定子磁鏈α、β軸分量，ψ為定子磁鏈，R為定子相電阻，n_p為轉子極對數，ω為轉子機械角速度，T_e為電磁轉矩，B_m為粘滯阻尼系數，E_α、E_β為電機的反電動勢α、β軸分量，是θ的估計值，K和P分別為增益矩陣和協方差矩陣，λ是遺忘因子，和蝸簧箱轉動慣量和轉矩的辨識值，T_s為采樣周期，k為采樣點，和表示和的辨識誤差，θ_ref、ω_ref、T_ref和ψ_ref分別為θ、ω、T和ψ的參考值，e_θ、e_ω、e_T和e_ψ為誤差變量，分別為θ_ref的一、二、三階導數，為的導數，k_θ、k_ω、k_T、k_ψ為正的控制增益，ψ_f為轉子永磁磁鏈，為u_α、u_β的參考值。

具體實施方式

本發明由以下技術方案實現：

1.機械彈性儲能系統數學建模

機械彈性儲能裝置儲能部分模型如圖1所示，電網通變頻器和PMSM相連，通過本發明控制策略，驅動PMSM實現的平穩儲能。

在儲能過程中，永磁同步電動機運行于電動機機狀態，永磁同步電動機在α、β軸坐標系下的數學模型可寫為：

定子電流方程

定子磁鏈方程

轉子運動方程

電磁轉矩方程

式中：i_α、i_β為定子α、β軸電流，L為定子電感，ψ_α、ψ_β為定子磁鏈α、β軸分量，ψ為定子磁鏈，R為定子相電阻，n_p為轉子極對數，ω為轉子機械角速度，u_α、u_β為定子電壓α、β軸分量，T為蝸簧箱機械轉矩，J為蝸簧箱轉動慣量，T_e為電磁轉矩，B_m為粘滯阻尼系數，E_α、E_β為電機的反電動勢。

儲能時，蝸簧箱作為負載，根據材料力學知識，其數學模型可通過機械轉矩T和轉動慣量J予以描述，如式(5)和(6)所示。

T＝T₀+cδ＝T₀+cωt (5)

其中，T₀為蝸簧儲能時的初始轉矩，ω、δ分別為蝸簧芯軸的轉速和轉過的角度，c為蝸簧轉矩系數，是一個常量，對于矩陣截面的蝸簧，E、b、h和l分別表示蝸簧材料的彈性模量、寬度、厚度和長度，t為時間，J_e為蝸簧完全釋放時的轉動慣量，n為蝸簧總的工作圈數。式(5)和式(6)表明，儲能過程中，作為負載的渦卷彈簧轉矩不斷增大，轉動慣量則逐漸減小。

公式(1)到(6)就構成了機械彈性儲能機組儲能部分全系統數學模型。

2.控制方案設計

2.1蝸簧箱轉矩和轉動慣量的同時辨識

鑒于遺忘因子遞推最小二乘法辨識的優越性，將其應用于實時辨識蝸簧箱的轉矩和轉動慣量。忽略B_m，PMSM轉子運動方程(3)可離散化為：

式中，T_s為采樣周期，k為采樣點。

令Δω(k)＝ω(k+1)-ω(k)，式(7)可表示為：

式中，

基于式(8)，采用帶遺忘因子的最小二乘算法去辨識θ，可得：

式中，式中，是θ的估計值，K和P分別為增益矩陣和協方差矩陣，λ是遺忘因子，需選擇接近于1的正數，通常不小于0.9，根據本文的實際情況，選擇λ＝0.9。

根據式(7)至式(11)，能夠辨識出蝸簧負載的轉矩和轉動慣量，分別用和表示。

2.2反推自適應控制器設計

根據反推控制原理，定義誤差變量e_θ、e_ω、e_T和e_ψ如下：

式中，θ_ref、ω_ref、T_ref和ψ_ref分別為θ、ω、T和ψ的參考值參考值。首先選取第一個lyapunov函數V₁如下：

對其求導可得：

取虛擬控制函數：

則：

其中，k_θ為正的控制增益。

將式(16)代入式(14)，可得：

選取第二個lyapunov函數V₂如下：

對其求導數，可得：

取：

假設：

則：

取虛擬控制函數：

其中：是β₁，β₂，β₃的估計值，假設：的估計誤差，定義

將(22)、(21)代入(19)可得：

其中:

選取第三個lyapunov函數V₃如下：

對其求導數，可得：

K₃＝2(ψ_αu_α+ψ_βu_β-Rψ_αi_α-Rψ_βi_β)

取：

其中：

其中：

將(27)、(26)代入(25)可得：

最終，lyapunov函數V₄如下：

其中：

且t₁,t₂,t₃＞0

對其求導可得：令：代入上式可得：

由于V有界，根據Barbalat定理，可得：

即e_θ,e_ω,e_T當t→∞時趨近于零，即工作圈數，角速度，轉矩均能跟蹤給定值。實施例子

對提出的控制方法進行實驗分析。永磁同步電動機有關參數為：定子每相電阻R＝2.875Ω；定子電感L＝0.05H；永磁體磁通ψ_f＝0.38Wb；轉子極對數n_p＝10；粘滯阻尼系數B_m＝0.0005N/rad/s；轉動慣量0.001kg·m²；蝸簧箱的設計與制造基于國標JB/T 7366-1994完成，使用蝸簧材料的參數為：彈性模量E＝2×10¹¹N/m²；寬度b＝0.050m；厚度h＝0.0018m；長度L＝14.639m；蝸簧轉矩系數c＝3.95N·m；蝸簧初始轉矩T₀＝5N·m，完全釋放后的轉動慣量J_e＝0.030kg·m²；彈簧總工作圈數n＝20r。定子磁鏈幅值為0.38Wb，PMSM速度參考信號采用如式(32)所示指令，運行時間為10min

ω_ref＝2r/min (32)

反推自適應直接轉矩控制參數取值為：k_θ＝0.01、k_ω＝3.37、k_T＝4.44、k_ψ＝10t₁＝4.52、t₂＝4.78、t₃＝1853.7，設計的反推控制器為：

其中：

利用實驗平臺進行實驗驗證，實驗結果如圖3至圖7。圖3可以看出辨識方法快速有效，辨識誤差較小。圖4可以看出工作圈數呈線性變化，無明顯的抖動，儲能過程比較平穩。圖5為轉速曲線，控制系統能夠較快的將轉速調整至給定值。圖6位電機輸出轉矩曲線，可以看出，電機轉矩能夠快速跟蹤儲能箱轉矩，保證儲能過程的平穩。圖7位定子A、B相電流曲線，電流幅值隨儲能過程的進行而逐漸增大，符合設計原理。總體上說，控制系統能夠快速匹配電機轉矩和儲能箱轉矩，實現儲能過程的控制要求。