一種混合交易模式下的網損分攤方法與流程

本發明涉及電力市場中網損分攤領域，具體涉及一種混合交易模式下的網損分攤方法。

背景技術：

在未來輸電開放的市場框架下，需解決的問題之一是如何將輸電損耗在輸電用戶(電能的生產方和使用方)中分攤，即輸電損耗分攤問題。雖然在電力市場的交易過程中，輸電網損耗成本只占全部成本中很小的一部分(一般來講輸電系統功率損耗占整個輸送容量的2-5％)，但其累計效應不容忽視，且網損分攤對于提高輸電定價有效性以及引導輸電用戶合理利用輸電資源具有重要作用，需要對其進行重點研究，以盡可能提高市場效率。

網損分攤方法的確定應以電力市場交易模式為前提，并在盡量滿足公平合理、快速高效、收支平衡、過程透明、經濟信號五條網損分攤原則的基礎上進行。目前應用較多的交易模式有：聯營交易模式、雙邊交易模式及聯營—雙邊混合交易模式，其中，聯營—雙邊混合交易模式符合我國大部分地區的實際情況。交易模式的不同關乎網損分攤的對象問題，在確定網損分攤方法時應首先予以考慮。

至今存在多種網損分攤方法，其中較經典的有五種，由于其不同的特點而適用于不同的交易類型。平均網損系數法是最早在電力工業聯營模式中采用的網損分攤方法，各發電機/負荷根據其功率占系統總發電功率/負荷功率的比例來分攤網損，但是存在交叉補貼現象，且不能將網損分攤至雙邊交易。潮流追蹤法可對各個支路功率如何分配至發電機/負荷節點進行詳細計算，但是在復雜電力網絡中進行潮流追蹤所需的數據量和計算量非常龐大，且無法追蹤雙邊交易對網損的影響。合同路徑法是針對電力市場中雙邊合同實施的網損分攤方法，假定電能只在合同中規定的連續路徑中流過，但是忽略了輸配電潮流對非合同路徑的影響，并且由于聯營模式不存在合同路徑而應用受限。邊際網損系數法根據節點注入功率的單位變化引起全網網損變化量的大小對各節點進行網損分攤，但是存在著所分攤網損可能存在巨大波動使得用戶風險提高、網損費用的過度回收等問題，且交易次序會對最終的分攤結果產生影響。基于博弈論的網損分攤方法利用了電力市場環境下交易與合作博弈模型的相似性對網損進行分攤，不受交易追加次序的影響，但是分攤過程的復雜性隨著交易個數的增長而迅速增大，在實際網絡中的運用受到一定限制。

技術實現要素：

本發明提供一種混合交易模式下的網損分攤方法，其目的是將聯營交易看作一筆交易，以直流潮流為假設前提，按照各個交易在每條支路上的潮流占比對精確計算的交流網損進行分攤，適用于聯營交易和雙邊交易混合交易模式。

本發明的目的是采用下述技術方案實現的：

一種混合交易模式下的網損分攤方法，其改進之處在于，包括：

分別獲取混合交易中雙邊交易和聯營交易在網絡結構中的潮流分布；

分別確定混合交易中雙邊交易和聯營交易在網絡結構中的分攤網損。

優選的，獲取混合交易中雙邊交易在網絡結構中的潮流分布，包括：

利用網絡轉換法將所述網絡結構轉換為樹狀網絡結構，并獲取所述網絡結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣；

根據混合交易中雙邊交易在所述樹狀網絡結構的潮流分布獲取混合交易中雙邊交易在所述網絡結構的潮流分布。

進一步的，所述利用網絡轉換法將所述網絡結構轉換為樹狀網絡結構，并獲取所述網絡結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣，包括：

獲取所述網絡結構的最小生成樹結構，并確定所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布間的關聯矩陣；

消除所述網絡結構的最小生成樹結構的環流，將所述網絡結構的最小生成樹結構轉換為樹狀網絡結構，并確定所述網絡結構的最小生成樹結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣；

利用所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布間的關聯矩陣和所述網絡結構的最小生成樹結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣確定所述網絡結構與所述樹狀網絡結構間的關聯矩陣。

進一步的，所述獲取所述網絡結構的最小生成樹結構，并確定所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布間的關聯矩陣，包括：

根據下式(1)獲取所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布的關聯矩陣C₁₂：

式(1)中，n為所述網絡結構中支路總數，fⁿ為所述網絡結構中第n個支路的潮流，p為所述網絡結構的最小生成樹結構中樹支總數，f′^p為所述網絡結構的最小生成樹結構中第p個樹支的潮流，q為所述網絡結構的最小生成樹結構中環流總數，f″^q為所述網絡結構的最小生成樹結構中第q個環流的潮流，n＝p+q。

進一步的，采用Kruskal算法、Boruvka算法或Prim算法獲取所述網絡結構的最小生成樹結構。

進一步的，所述消除所述網絡結構的最小生成樹結構的環流，將所述網絡結構的最小生成樹結構轉換為樹狀網絡結構，并確定所述網絡結構的最小生成樹結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣，包括：

所述網絡結構的最小生成樹結構滿足：Δ₂＝X₂₂·F²，其中，Δ₂為所述網絡結構的最小生成樹結構中電壓相角差，X₂₂為所述網絡結構的最小生成樹結構中阻抗矩陣，所述網絡結構的最小生成樹結構的潮流分布F²＝[F_ibt,F_ic]^T，所述網絡結構的最小生成樹結構的樹支的潮流分布F_ibt＝[f′¹...f′^p]^T，所述網絡結構的最小生成樹結構的環流的潮流分布F_ic＝[f″¹...f″^q]^T，p為所述網絡結構的最小生成樹結構中樹支總數，f′^p為所述網絡結構的最小生成樹結構中第p個樹支的潮流，q為所述網絡結構的最小生成樹結構中環流總數，f″^q為所述網絡結構的最小生成樹結構中第q個環流的潮流；

所述網絡結構的最小生成樹結構中電壓相角差其中，Δ_ibt為所述網絡結構的最小生成樹結構中樹支支路相角差；

所述網絡結構的最小生成樹結構中阻抗矩陣其中，X₁₁為所述網絡結構中支路電抗矩陣，C₁₂為所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布的關聯矩陣；

將所述網絡結構的最小生成樹結構中阻抗矩陣X₂₂拆分為四部分，則

利用所述網絡結構的最小生成樹結構的樹支的潮流分布F_ibt表示所述網絡結構的最小生成樹結構的環流的潮流分布F_ic，公式為：

式(2)中，X_{ic_ibt}為所述網絡結構的最小生成樹結構中阻抗矩陣X₂₂的左下部分，X_{ic_ic}為所述網絡結構的最小生成樹結構中阻抗矩陣X₂₂的右下部分，

將所述網絡結構的最小生成樹結構的潮流分布F²＝[F_ibt,F_ic]^T中的環流的潮流分布F_ic用所述網絡結構的最小生成樹結構的樹支的潮流分布F_ibt表示，即其中，I為單位矩陣，F_ibt＝F³，F³為所述樹狀網絡結構的潮流分布；

則所述網絡結構的最小生成樹結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣

進一步的，按下式(3)確定所述網絡結構與所述樹狀網絡結構間的關聯矩陣C₁₃：

C₁₃＝C₁₂·C₂₃ (3)

式(3)中，C₁₂為所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布的關聯矩陣，C₂₃為所述網絡結構的最小生成樹結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣。

8.如權利要求2所述的方法，其特征在于，根據下式(4)獲取混合交易中雙邊交易在所述網絡結構的潮流分布F¹：

F¹＝C₁₃·F³ (4)

式(4)中，C₁₃為所述網絡結構與所述樹狀網絡結構間的關聯矩陣，F³為混合交易中雙邊交易在所述樹狀網絡結構的潮流分布。

優選的，獲取混合交易中聯營在網絡結構中的潮流分布，包括：

按下式(5)建立網絡結構的節點導納矩陣B：

式(5)中，i、j∈[1,m]，m為網絡結構的節點總數，B(i,i)為所述節點導納矩陣B的第i行第i列元素，B(i,j)為所述節點導納矩陣B的第i行第j列元素，x_ij為節點i與j之間的電抗；

在m個節點中隨機選取一個節點k作為平衡節點，令節點k的電壓相角為零，并刪除所述節點導納矩陣B中節點k對應的行和列的元素，獲取網絡結構中除節點k外節點的導納矩陣B₀；

獲取網絡結構中除節點k外節點的阻抗矩陣X，其中，

獲取網絡結構中除節點k外節點的電壓相角列矢量θ，其中，θ＝XP^sp，P^sp為網絡結構中除節點k外節點的注入功率列矢量；

按下式(6)獲取混合交易中聯營在網絡結構中的潮流分布：

式(5)中，F_ij為節點i與j之間的直流潮流，θ_i為節點i的電壓相角，θ_j為節點j的電壓相角，x_ij為節點i與j之間的電抗，若i＝k，則θ_i＝0，若j＝k，則θ_j＝0，k∈[1,m]。

優選的，所述分別確定混合交易中雙邊交易和聯營交易在網絡結構中的分攤網損，包括：

按下式(7)確定混合交易中第t組雙邊交易在網絡結構中的分攤網損ΔP_t：

式(7)中，s∈[1,n]，n為網絡結構中支路總數，為混合交易中第t組雙邊交易在網絡結構中第s條支路的潮流，為混合交易中聯營交易在網絡結構中第s條支路的潮流，為網絡結構中第s條支路的有功網損；

按下式(8)確定混合交易中聯營交易在網絡結構中的分攤網損ΔP_p：

本發明的有益效果：

本發明提供的技術方案簡單易行，其流程化思想可為進一步的程序開發打下基礎，由于關聯矩陣的獲取只與網絡結構有關，與交易情況無關，因此，避免了交易中多次潮流計算，且不用考慮交易的交叉影響。該方法考慮了某些交易產生的逆向流，并對提供反向潮流的交易給予了鼓勵。方法綜合反映了交易量與交易各方的電氣距離等因素，并且最終的分攤結果是收支平衡的，實現了每筆交易對系統總交流網損的公平分攤，充分體現誰使用誰付錢，用多少付多少的分攤原則。由于方法是按每筆交易在每條支路潮流所占比例來分攤網損，對于市場參與者來說較易接受，可為實際系統中電力交易提供一定參考。

附圖說明

圖1是本發明一種混合交易模式下的網損分攤方法的流程圖；

圖2是本發明實施例中參考系1結構示意圖；

圖3是本發明實施例中參考系2結構示意圖；

圖4是本發明實施例中參考系3結構示意圖；

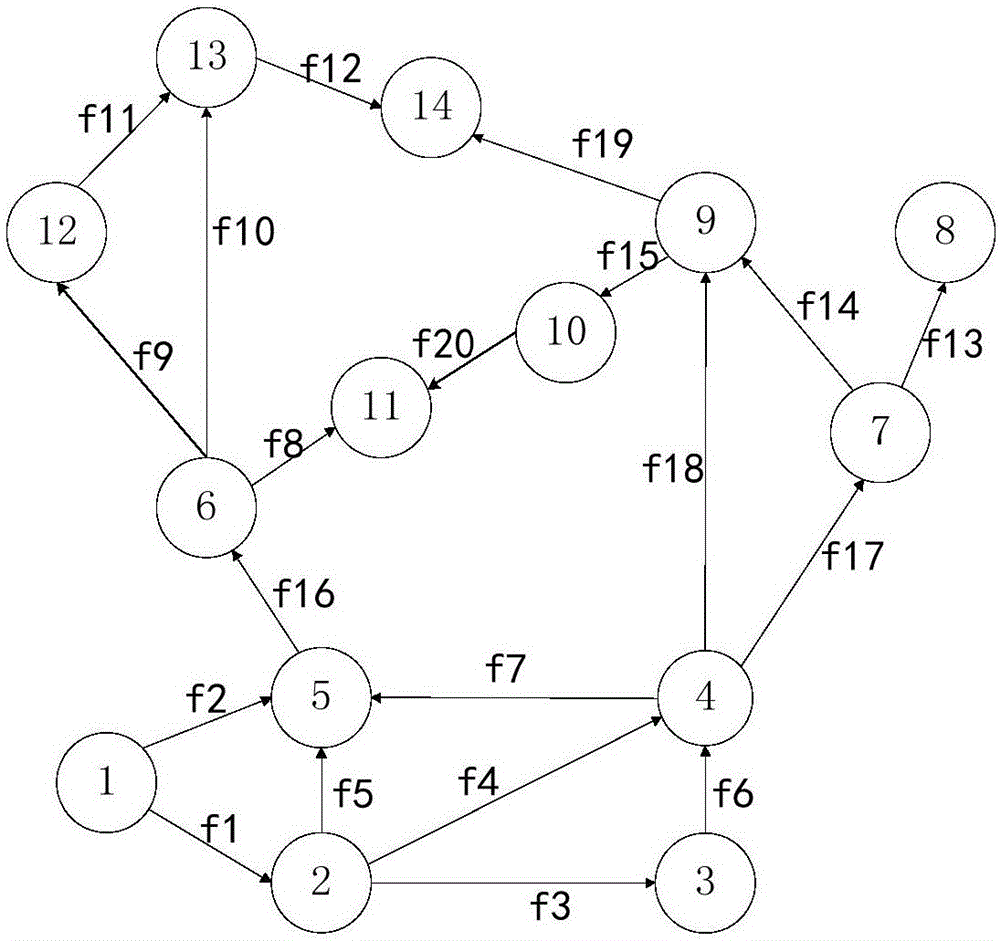
圖5是本發明實施例中IEEE 14節點標準網絡結構示意圖。

具體實施方式

下面結合附圖對本發明的具體實施方式作詳細說明。

為使本發明實施例的目的、技術方案和優點更加清楚，下面將結合本發明實施例中的附圖，對本發明實施例中的技術方案進行清楚、完整地描述，顯然，所描述的實施例是本發明一部分實施例，而不是全部的實施例。基于本發明中的實施例，本領域普通技術人員在沒有做出創造性勞動前提下所獲得的所有其它實施例，都屬于本發明保護的范圍。

本發明提供的一種混合交易模式下的網損分攤方法，如圖1所示，包括：

101.分別獲取混合交易中雙邊交易和聯營交易在網絡結構中的潮流分布；

102.分別確定混合交易中雙邊交易和聯營交易在網絡結構中的分攤網損。

具體的，所述混合交易包括雙邊交易和聯營交易，假設取混合交易中雙邊交易為k組，混合交易中聯營交易為1組，則所述步驟101中，獲取所述混合交易中各組雙邊交易在網絡結構中的潮流分布，包括：

利用網絡轉換法將所述網絡結構轉換為樹狀網絡結構，并獲取所述網絡結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣；

根據混合交易中雙邊交易在所述樹狀網絡結構的潮流分布獲取混合交易中雙邊交易在所述網絡結構的潮流分布。

進一步的，每筆雙邊交易合同中由于確定了固定的發電商、用電商、交易功率和合同路徑，因此所有雙邊交易組成了一個金融性網絡，可用“運輸網絡”對其進行建模。運輸網絡的特點是“商品”可以按照預先指定的路徑由一個節點傳輸到另一個節點，通常可用加權有向圖表示。而電力網絡與普通運輸網絡最大的不同在于電功率在線路上的傳輸受線路阻抗限制，遵循基爾霍夫定律，導致了電功率不能僅僅在預先指定的路徑——即合同路徑上傳輸，而是會分布在整個電網絡上，合同路徑之外的潮流被稱作“環流”。為了對雙邊交易進行有效建模，消去環流影響，需將網狀的電網絡通過一系列等效計算轉化成樹狀網，樹狀網由于每兩個節點間有且只有一條通路從而能夠有效地對雙邊交易進行簡單描述，這個轉化過程就被稱作網絡轉換法。因此，所述利用網絡轉換法將所述網絡結構轉換為樹狀網絡結構，并獲取所述網絡結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣，包括：

獲取所述網絡結構的最小生成樹結構，并確定所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布間的關聯矩陣；

消除所述網絡結構的最小生成樹結構的環流，將所述網絡結構的最小生成樹結構轉換為樹狀網絡結構，并確定所述網絡結構的最小生成樹結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣；

利用所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布間的關聯矩陣和所述網絡結構的最小生成樹結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣確定所述網絡結構與所述樹狀網絡結構間的關聯矩陣。

其中，所述網絡結構的潮流分布，即為網絡結構的支路潮流，所述網絡結構的最小生成樹結構的潮流分布，即為所述網絡結構的樹枝潮流和環流，所述樹狀網絡結構的潮流分布，即為所述網絡結構的等效樹支潮流，該樹支潮流是根據交易情況直接賦值的；

網絡轉換法實現了網狀網絡到樹狀網絡的等效轉化，整個轉化包含三個參考系和兩步變換過程。參考系1代表所述網絡結構，網絡上每條支路的有功潮流用矢量F¹表示，支路兩端電壓相角差記為矢量Δ₁，支路阻抗矩陣記為X₁₁(由于假設條件中電阻遠小于電抗，因此X₁₁主對角線上僅考慮支路電抗)；參考系2是介于網狀網絡和樹狀網絡之間的網絡模型，即上述操作過程中所述網絡結構的最小生成樹結構，由承載雙邊交易的樹支和代表環流的基本回路組成，同樣的，有功潮流記為F²，電壓相角差記為Δ₂，阻抗矩陣記為X₂₂，參考系1與參考系2之間的關聯矩陣記為C₁₂；參考系3代表完全消去環流影響的樹支網絡，即上述操作過程中的所述樹狀網絡結構，同樣可用三個基本特征量描述：F³、Δ₃與X₃₃，參考系2到參考系3的轉換矩陣記為C₂₃。

根據基爾霍夫定律與功率守恒定律，每兩個參考系中的基本量具有如下關系：

具體的，所述獲取所述網絡結構的最小生成樹結構，并確定所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布間的關聯矩陣，包括：

根據下式(1)獲取所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布的關聯矩陣C₁₂：

式(1)中，n為所述網絡結構中支路總數，fⁿ為所述網絡結構中第n個支路的潮流，p為所述網絡結構的最小生成樹結構中樹支總數，f′^p為所述網絡結構的最小生成樹結構中第p個樹支的潮流，q為所述網絡結構的最小生成樹結構中環流總數，f″^q為所述網絡結構的最小生成樹結構中第q個環流的潮流，n＝p+q。

其中，可以采用Kruskal算法、Boruvka算法或Prim算法獲取所述網絡結構的最小生成樹結構。

即參考系1到參考系2的轉化，例如，如圖2所示，參考系1為IEEE 14節點標準算例，支路的電抗參數已知，網絡中每條支路潮流及假設方向用實線箭頭表示。參考系1到參考系2的轉化是將原網狀網絡轉化成樹狀網絡與環流的疊加，而一旦樹支被選擇出來，環流即被唯一確定。考慮到由于樹支的選取只對中間過程產生影響，不會影響最終的潮流運算結果，并且考慮到潮流總是趨向于流經阻抗最小的支路，因此樹支的選取按照圖論里“最小生成樹”原則進行。

最小生成樹，即各邊電抗之和最小的生成樹，構造準則有3條：

(1)必須只使用該網絡中的邊來構造最小生成樹。

(2)必須使用且僅使用n-1條邊來連接網絡中的n個頂點。

(3)不能使用產生回路的邊。

構造最小生成樹的算法目前發展已較為成熟，主要有：Kruskal算法、Boruvka算法和Prim算法，其中Kruskal算法主要適用于稀疏圖，Boruvka算法與Kruskal算法類似，Prim算法主要適用于稠密圖，可根據圖的稀疏程度選擇合適的算法。

在此運用Prim算法構造最小生成樹，結果如圖3中實線箭頭所示；樹支以外的支路稱之為連支，在圖3中用虛線箭頭表示。每當在樹上加一條連支時，將使相應的兩個節點之間增加一條由所加連支構成的路徑，則必然形成一個回路。只含有一條連支的回路稱為基本回路，在網絡轉換法中稱之為“環流”，由于各基本回路彼此包含有不同的連支，因此環流是相互獨立的，且環流的方向與連支的方向相同，如圖3所示。至此，網絡中實際的物理潮流F¹已被分解為樹支潮流F^ibt與環流F^ic的代數和，方向相同為正，方向相反為負。再例如，原網絡中的f¹可被分解為f^1’減去f^c1，f^c1符號為負是因為f^c1與f¹方向相反。將20條原網絡支路潮流分別用樹支潮流與環流表示：

其中，F¹＝[f¹，f²，f³，…，f¹⁹，f²⁰]^T表示原網絡20條支路潮流，F²＝[f^1’，f^2’，…，f^13’，f^c1，…，f^c7]^T＝[F^ibt∣F^ic]^T，F^ibt＝[f^1’，f^2’，…，f^13’]^T表示樹支潮流，F^ic＝[f^c1，…，f^c7]^T表示環流。至此，原網絡支路潮流已經被樹支潮流與環流所表示，即完成了參考系1到參考系2的轉換。

所述消除所述網絡結構的最小生成樹結構的環流，將所述網絡結構的最小生成樹結構轉換為樹狀網絡結構，并確定所述網絡結構的最小生成樹結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣，包括：

所述網絡結構的最小生成樹結構滿足：Δ₂＝X₂₂·F²，其中，Δ₂為所述網絡結構的最小生成樹結構中電壓相角差，X₂₂為所述網絡結構的最小生成樹結構中阻抗矩陣，所述網絡結構的最小生成樹結構的潮流分布F²＝[F_ibt,F_ic]^T，所述網絡結構的最小生成樹結構的樹支的潮流分布F_ibt＝[f′¹...f′^p]^T，所述網絡結構的最小生成樹結構的環流的潮流分布F_ic＝[f″¹...f″^q]^T，p為所述網絡結構的最小生成樹結構中樹支總數，f′^p為所述網絡結構的最小生成樹結構中第p個樹支的潮流，q為所述網絡結構的最小生成樹結構中環流總數，f″^q為所述網絡結構的最小生成樹結構中第q個環流的潮流；

所述網絡結構的最小生成樹結構中電壓相角差其中，Δ_ibt為所述網絡結構的最小生成樹結構中樹支支路相角差；

所述網絡結構的最小生成樹結構中阻抗矩陣其中，X₁₁為所述網絡結構中支路電抗矩陣，C₁₂為所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布的關聯矩陣；

將所述網絡結構的最小生成樹結構中阻抗矩陣X₂₂拆分為四部分，則

利用所述網絡結構的最小生成樹結構的樹支的潮流分布F_ibt表示所述網絡結構的最小生成樹結構的環流的潮流分布F_ic，公式為：

式(2)中，X_{ic_ibt}為所述網絡結構的最小生成樹結構中阻抗矩陣X₂₂的左下部分，X_{ic_ic}為所述網絡結構的最小生成樹結構中阻抗矩陣X₂₂的右下部分，

將所述網絡結構的最小生成樹結構的潮流分布F²＝[F_ibt,F_ic]^T中的環流的潮流分布F_ic用所述網絡結構的最小生成樹結構的樹支的潮流分布F_ibt表示，即其中，I為單位矩陣，F_ibt＝F³，F³為所述樹狀網絡結構的潮流分布；

則所述網絡結構的最小生成樹結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣

即參考系2到參考系3的轉化，為將參考系2轉化為參考系3，需消去環流影響，即可將環流用樹支潮流線性表示。在參考系2中，存在如下等式關系：

Δ₂＝X₂₂·F²

進一步可詳細寫為：

由于遵循KVL，環流的電壓相角差為零，因此上式是線性相關的，可得到如下關系式：

將環流F^ic寫成了樹支潮流F^ibt的表達式，因此，可將參考系2中的7個環流全部用樹支潮流表示，即得到了參考系2到參考系3的關聯矩陣，轉換過程如下式所示：

即：

F²＝C₂₃·F³

通過環流的消除，參考系2被轉化為僅含樹支潮流的參考系3，如圖4所示。

參考系3消除了KVL的影響，且兩節點之間有且只有一條通路，因此可看作上文所說的“運輸網絡”。而關聯矩陣C₁₂與C₂₃記錄了轉化過程中潮流的等效變化過程，存儲了參考系1向參考系3轉化的唯一信息，因此，由原網絡到樹狀網絡的轉化過程可由關聯矩陣C₁₃表示，按下式(3)確定所述網絡結構與所述樹狀網絡結構間的關聯矩陣C₁₃：

C₁₃＝C₁₂·C₂₃ (3)

式(3)中，C₁₂為所述網絡結構的潮流分布與所述網絡結構的最小生成樹結構的潮流分布的關聯矩陣，C₂₃為所述網絡結構的最小生成樹結構的潮流分布與所述樹狀網絡結構的潮流分布間的關聯矩陣。

根據下式(4)獲取混合交易中雙邊交易在所述網絡結構的潮流分布F¹：

F¹＝C₁₃·F³ (4)

式(4)中，C₁₃為所述網絡結構與所述樹狀網絡結構間的關聯矩陣，F³為混合交易中雙邊交易在所述樹狀網絡結構的潮流分布。

根據每組雙邊交易情況依次對F³進行賦值后，經過與關聯矩陣的相乘即可得到每組雙邊交易在原網絡中的潮流分布。且C₁₃的求取與交易情況無關，只與網絡拓撲結構有關，因此當交易情況變化時不需要重復求取，大大簡化了計算過程。

聯營交易與雙邊交易的交易特點有較大差異，雙邊交易是點對點交易，每組雙邊交易有其對應的發電商與用電商；而參與聯營交易的發電商與用電商不存在一一對應關系，是通過統一的“電力庫”進行電力買賣，只能保證電力是收支平衡的。因此當整個網絡中同時存在這兩種交易模式時，必須將二者區別對待。雙邊交易處理方法是基于直流潮流假設，由于直流潮流具有可疊加性，因此使用直流潮流法計算聯營交易在原網絡上的潮流分布，所得結果可與雙邊交易統一考慮從而進行下一步的網損分攤。獲取混合交易中聯營在網絡結構中的潮流分布，包括：

按下式(5)建立網絡結構的節點導納矩陣B：

式(5)中，i、j∈[1,m]，m為網絡結構的節點總數，B(i,i)為所述節點導納矩陣B的第i行第i列元素，B(i,j)為所述節點導納矩陣B的第i行第j列元素，x_ij為節點i與j之間的電抗；

在m個節點中隨機選取一個節點k作為平衡節點，令節點k的電壓相角為零，并刪除所述節點導納矩陣B中節點k對應的行和列的元素，獲取網絡結構中除節點k外節點的導納矩陣B₀；

獲取網絡結構中除節點k外節點的阻抗矩陣X，其中，

獲取網絡結構中除節點k外節點的電壓相角列矢量θ，其中，θ＝XP^sp，P^sp為網絡結構中除節點k外節點的注入功率列矢量；

按下式(6)獲取混合交易中聯營在網絡結構中的潮流分布：

式(5)中，F_ij為節點i與j之間的直流潮流，θ_i為節點i的電壓相角，θ_j為節點j的電壓相角，x_ij為節點i與j之間的電抗，若i＝k，則θ_i＝0，若j＝k，則θ_j＝0，k∈[1,m]。

針對兩種交易模式的不同特點用不同的方法分別求得每組雙邊交易和聯營交易在網絡中的潮流分布，接下來要結合交易的具體數據建立網損分攤模型并根據各組交易在總交易中的潮流占比來對每條支路的交流網損進行分攤，所述步驟102，包括：

按下式(7)確定混合交易中第t組雙邊交易在網絡結構中的分攤網損ΔP_t：

式(7)中，s∈[1,n]，n為網絡結構中支路總數，為混合交易中第t組雙邊交易在網絡結構中第s條支路的潮流，為混合交易中聯營交易在網絡結構中第s條支路的潮流，為網絡結構中第s條支路的有功網損；

其中，為按照交流潮流計算得到的；

按下式(8)確定混合交易中聯營交易在網絡結構中的分攤網損ΔP_p：

根據如圖5所示的IEEE 14節點標準網絡交易的實際數據求得最終的網損分攤結果，節點1、2、3、6、8為發電機節點，其它節點為負荷節點，參與雙邊交易和聯營交易節點及其交易量如表1和表2所示：

表1 IEEE-14節點系統的雙邊交易數據

表2 IEEE-14節點系統的聯營交易數據

按照上文所述方法計算各筆雙邊交易和聯營交易(看作一筆交易)在每條支路上潮流所占比例(也即各筆交易在每條支路上網損所占比例)與最終計算所得分攤的總網損如表3和表4所示。

表3各筆雙邊交易和聯營交易支路潮流(網損)占比

表4各筆雙邊交易和聯營交易應當分攤的總網損

由表3可以看出，就每一條支路來說，不僅將各筆交易在每條支路潮流上的占比求和結果為1，并且潮流(網損)占比有正有負。在實際，存在多個交易同時利用一條線路、而且某些交易在該線路中引起了逆向潮流的情況，由該發明方法計算得到的該筆交易在支路上的潮流(網損)占比呈負值。客觀上，這就表示給提供反向潮流的交易給予了鼓勵，給其分攤了較少的費用甚至分攤負的費用，這符合反向潮流的存在可以增大輸電系統的輸送能力、在一些線路上減小輸電損耗的實際情況。由表4可以看出，每筆交易應分攤的網損可綜合反映其交易量與交易各方的電氣距離等因素，同時，將各筆交易應分攤的網損求和，數值等于系統總的交流網損。這就說明，本專利所提出的方法是合理的，并且是收支平衡的，不至于電網公司過多地回收網損費用，也易于交易各方接受。

最后應當說明的是：以上實施例僅用以說明本發明的技術方案而非對其限制，盡管參照上述實施例對本發明進行了詳細的說明，所屬領域的普通技術人員應當理解：依然可以對本發明的具體實施方式進行修改或者等同替換，而未脫離本發明精神和范圍的任何修改或者等同替換，其均應涵蓋在本發明的權利要求保護范圍之內。