一種主配網故障恢復優化調度的方法與流程
本發明涉及電力系統故障恢復領域,特別是涉及一種主配網故障恢復優化調度的方法。
背景技術:
故障恢復技術是電網事故響應決策技術的核心部分。電網事故響應決策技術是指當主網和配網實際發生故障后,將電網的實時運行狀態與預設的電網運行狀態相匹配,得到該運行狀態下電網的故障最優恢復控制策略,自主快速地向主網運行人員和配網運行人員提供緊急恢復控制策略,以提高電網整體的運行穩定性。然而電網事故響應決策匹配的整個過程由于復雜程度和不確定因素等限制,難以用數學模型來描述。近年來,隨著人工智能技術的不斷發展,以支持向量機技術、決策樹技術和人工神經網絡技術為代表的人工智能技術在電力系統領域得到廣泛應用。基于人工智能技術的電網事故響應決策算法無需建立詳細的電力系統模型,而是從大量的樣本中獲取電網運行狀態的知識,通過類比和機器學習等功能精細規則,實現事故自主匹配響應和決策,因此人工智能技術在電網事故響應決策中的研究具有重要意義。
目前,人工智能技術已經廣泛在電力系統故障恢復中廣泛使用。天津大學的林濟鏗、余貽鑫等人提出了一種新型的決策樹-人工神經網絡混合機構模式改進神經網絡訓練學習,實現電力系統動態安全評價。清華大學的戴遠航、閔勇等人提出在安全域的概念下基于多支持向量機技術進行電力系統暫態穩定評估的方法,利用了網格法對支持向量機進行參數尋優并訓練支持向量機,綜合訓練后的支持向量機,實現電力系統暫態穩定評估。現有技術中提出應用支持向量機模型,依照關鍵斷面是否出現對電網安全 運行支持分層,對海量電網運行狀態進行分類,形成不同形式的精細規則,建立電網安全運行知識庫。華北電力大學的陳小平、顧雪平等人在網絡重構的基礎上,提出了基于遺傳模擬退火算法的負荷恢復計劃制定方法,利用增廣潮流引入系統頻率的計算,采用罰函數的形式處理各種系統約束,通過適應值函數的計算得到系統允許條件下的最優恢復路徑和最大允許恢復負荷量。此外,以基于SCADA信息快速判別電網穩定薄弱環節為目標,提出基于決策樹的產生式穩定判別規則提取方法,實現電力系統暫態穩定評估。
然而,采用人工智能的技術求解主配網一體化的故障恢復問題,效率并不高,且不能保證求解的結果一定是最佳的求解結果。采用主配網全局優化模型來求解主配網一體化的故障恢復問題,不僅規模非常龐大,涉及主配網多個電壓等級,而且由于一般而言主配網分別采用單相和三相模型,問題模型非常復雜。主網中的變壓器抽頭和電容電抗器為離散控制變量,而且配網中存在開關打開和閉合這個離散控制變量,模型本身也不具有封閉的表達形式,不可能統一求解。
技術實現要素:
為解決上述技術問題,本發明將問題分解為一個主網和多個配網各自獨立的子優化問題及其通過主配網之間的分解協調來求解,從而降解了電網的求解規模,提高計算效率和精確性。
本發明的目的是提供一種將主網和配網的優化調度問題分開迭代計算,計算效率高、計算準確性高的主配網故障恢復優化調度的方法。
為實現上述發明目的,本發明提供的技術方案是:
一種主配網故障恢復優化調度的方法,包括以下步驟:步驟一、求解主網的故障恢復優化調度子問題,將公共耦合節點(Point of Common Coupling,PCC)點的狀態變量傳遞給各個配網;
步驟二、依據主網傳遞的PCC點的狀態變量,求解連接主網的各個配網的故障優化子問題,并將PCC點的狀態變量返回給主網;
步驟三、判斷PCC點的前后誤差,如果誤差超過收斂依據,返回步驟一,在收斂依據范圍內則結束計算。
進一步地,在步驟一中,主網層的優化調度子問題的數學模型寫為:
min CT
s.t.fT,p(xpcc,xT)=0
fT,q(xpcc,xT)=0
PT,j,min≤PT,g,j≤PT,j,max
VT,i,min≤VT,i≤VT,i,max
IT,l(xT,xpcc)≤IT,l,max
kT,min≤kT,g≤kT,max
其中,CT為主網的目標函數;xpcc為PCC點的狀態變量,xT為主網的狀態變量,fT,p(xpcc,xT)為不含PCC點的主網潮流方程;PT,g,j為主網中第j個發電機的有功出力,PT,g,min和PT,g,max為發電機的有功出力上下限;QT,g(xT,xpcc)為主網中發電機的無功出力,QT,g和為發電機的無功出力上下限;VT,i為主網中第i個節點的電壓,VT,i,max和VT,i,min為該節點的電壓上下限;為主網中第i條線路的電流值,為該線路的電流上限;kT,g為主網變壓器抽頭的檔位,kT,min和kT,max為主網的變壓器抽頭的上下限;QT,C為主網電容器投切的無功功率,和QT,C為電容器投切的上下限。
進一步地,在步驟一中,主網層智能體優化調度子問題的求解,采用原對偶內點法內嵌二次罰函數,進行松弛變量、拉格朗日乘子和各變量初值的初始化后迭代計算,公式為
其中,I表示單位矩陣;L、U、S為松弛變量l、u、s組成的對角矩陣;Z、W、T為拉格朗日乘子z、w、t組成的對角矩陣;x為狀態變量;y為拉格朗日乘子;和q(x)為不等式約束的導數矩陣;為等式約束的導數矩陣;
其他的有
Ly=h(x)=0
Lz=g(x)-l-g=0
Lt=q(x)+s-μe=0
其中,g和為不等式約束的上下限;μ為障礙函數。
進一步地,在步驟一中,變壓器抽頭和電容電抗等離散控制變量,采用內嵌二次罰函數法進行處理,離散控制的虛擬費用使用基于正曲率二次罰函數進行模擬;
在滿足最優解處起作用的電壓不等式約束集被基本鎖定時,以及離散控制變量的矯正量Δb需小于一個門檻值δ時,將二次罰函數引入。
進一步地,在步驟一中,自動修正罰子大小的公式為:
式中,μmax和μmin分別是最大、最小離散罰子(其數值分別可取100和10);Step為迭代步長。
當離散變量b1在罰函數作用下向中心b1運動時,罰子自動增大,使其加快到達b1;當b1向相反方向運動時,罰子自動減小,而使其加快向全局最優方向運動。
進一步地,在步驟一中,在內點法最優潮流解算過程中,當第k次主迭代完成以后,按以下步驟執行:
步驟3a判斷一階最優化條件是否已滿足。是則結束解算,否則繼續;
步驟3b判斷離散變量是否已越上或下邊界,是則引入邊界罰函數處理,否則繼續;
步驟3c判斷離散變量是否已引入了罰函數,是則轉入步驟3e,否則繼續;
步驟3d判斷離散罰函數引入的條件是否已滿足,是則繼續,否則轉入步驟3f;
步驟3e計算罰子幅值;
步驟3f引入二次罰函數,進行離散化處理;
步驟3g繼續第K+1次主迭代,回到步驟3a。
進一步地,在步驟二中,解決配網的供電區內分布式電源與負荷的優化調度子問題,數學模型為:
min CD,i
ΔPDR,j≤ΔPDR,j,max
其中,CD,i表示第i個配網的目標函數;和分別為PCC點的潮流方程的有功功率方程和無功功率方程,xT為主網的狀態變量,為第i個配網的PCC點的狀態變量,為第i個配網的狀態變量;和為第i個配網不含PCC點潮流方程的有功功率方程和無功功率方程;為配網變壓器抽頭的檔位,和為配網的變壓器抽頭的上下限;為第i個配網中電容器的投入無功功率,和為電容器投入的上下限; 為第i個配電網中分布式電源DG有功出力,和為DG的有功出力上下限;表示第i個配網中所有DG需滿足的不等式約束,因不同DG類型而異;ΔPDR,j,max和ΔPDR,j分別為第j個需求側響應的最大可控功率和實際調節功率值;為配網中第j個節點的電壓,和 為該節點的電壓上下限;為配網中第i條線路的電流值, 為該線路的電流上限;為網絡拓撲約束,即保證重構后的配網依然為輻射狀的連通網絡,無孤島存在,和為第i個配網的電導和電納約束。
進一步地,在步驟二中,配網智能體子優化問題的目標函數為
CD,i=ω1Cldsd+ω2CDG+ω3Closs+ω4Cbal+ω5CDR+ω5Cbreaker
式中,ω表示子目標的權重系數,Cldsd表示最小失負荷的目標函數,CDG表示發電經濟性的目標函數;Closs表示有功損耗的目標函數,Cbal表示負荷均衡化率的目標函數,CDR表示需求側響應的目標函數,Cbreaker表示最小開關動作次數目標函數。
進一步地,在步驟二中,采用分支定界-原對偶內點法求解配網層智能體優化調度子問題,通過分支使離散變量逐步逼近離散值,得到僅含連 續變量的優化松弛子問題,采用原對偶內點法進行求解,并將不滿足約束的子問題進行剪支。
進一步地,在步驟三中,判斷PCC點的前后誤差的公式為:
式中,ε為收斂精度,為PCC點的電壓幅值。
采用上述技術方案,本發明具有如下有益效果:
第一,本發明的技術方案將主網和配網的優化調度問題分開迭代計算但綜合考慮了主網和配網之間的相互影響,提高計算效率的同時也保證了計算的準確性。
第二,本發明將主配網一體化的故障恢復問題分解為一個主網和多個配網各自獨立的子優化問題,通過主配網之間的分解協調來求解,降低計算量,提高計算精準性,更加可靠地保障電網運行的安全性。
附圖說明
圖1為本發明實施例中罰幅修正的函數圖;
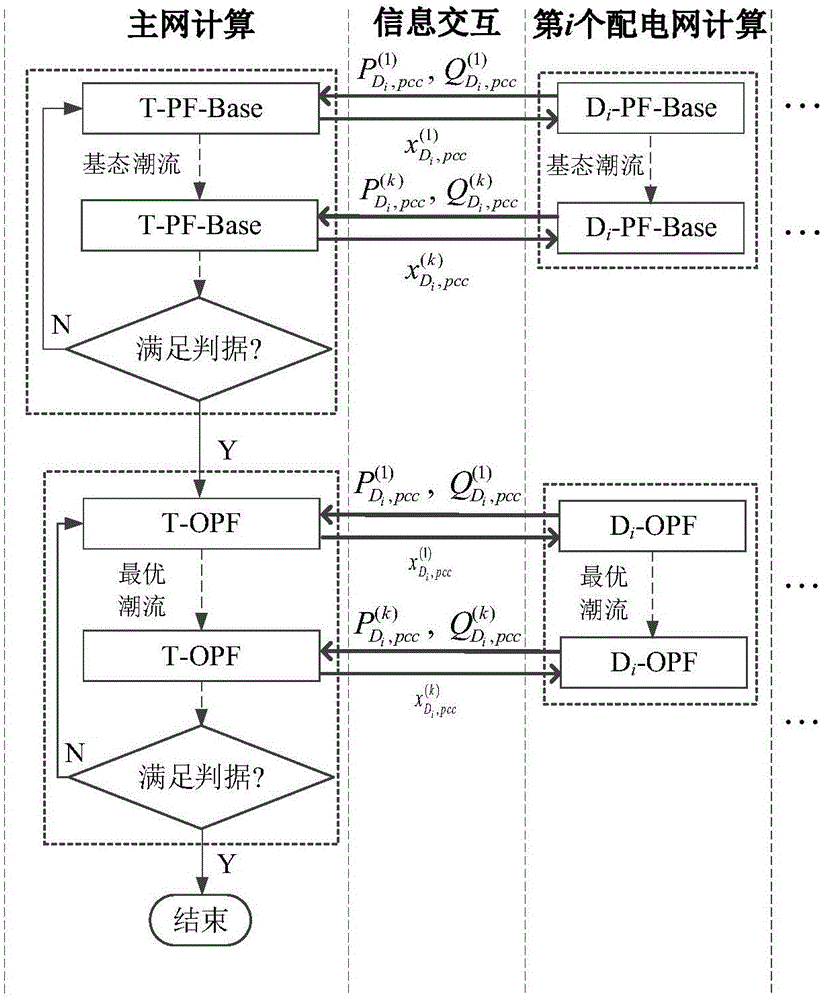
圖2為本發明實施例中主配網一體化分布式最優潮流的計算流程圖;
圖3為本發明實施例中開關狀態分支方法的示意圖;
圖4為本發明實施例中另一種開關狀態分支方法的示意圖。
具體實施方式
為了使本發明的目的、技術方案及優點更加清楚明白,下面結合附圖及實施例,對本發明進行進一步詳細說明。應當理解,此處所描述的結構圖及具體實施例僅用以解釋本發明,并不用于限定本發明。
本發明提供了一種主配網故障恢復優化調度的方法,包括以下步驟:
步驟一、求解主網的故障恢復優化調度子問題,將邊界點PCC點的狀態變量傳遞給各個配網;
步驟二、依據主網傳遞的PCC點的狀態變量,求解連接主網的各個配網的故障優化子問題,并將PCC點的狀態變量返回給主網;
步驟三、判斷PCC點的前后誤差,如果誤差超過收斂依據,返回步驟一,在收斂依據范圍內則結束計算。
實施例1
在步驟一中,主網的優化調度子問題的數學模型可寫為:
min CT
s.t.fT,p(xpcc,xT)=0
fT,q(xpcc,xT)=0
PT,j,min≤PT,g,j≤PT,j,max
VT,i,min≤VT,i≤VT,i,max
IT,l(xT,xpcc)≤IT,l,max
kT,min≤kT,g≤kT,max
優選地,主網的目標函數可以為網損最小:
CT=Closs
目標函數也可以為控制成本最小:
其中,cT,g,j為主網中第j臺發電機的控制成本系數。
主網智能體的優化調度子問題實質上就是一個典型的輸電網OPF問題。其求解時,與各配網接口處的PCC節點類型為PQ節點,等值負荷功率已知,由配網智能體優化子問題的結果給定。
主網層智能體優化調度子問題的求解是混合整數規劃問題,本發明采用原對偶內點法內嵌二次罰函數的方法來求解。先假定所有變量為連續變量,且控制變量和狀態變量合寫為:
將子問題模型中的目標函數簡寫為f(x),等式約束簡寫為h(x)=0,不等式約束簡寫為不等式約束可簡寫為q(x)≤0。在用原對偶內點法進行計算時,首先引入松弛變量u=[u1,…,ur]T,l=[l1,…,lr]T, 將上述不等式約束轉化為等式約束:
g(x)-l=g
q(x)+s=ξ
其中:ξ為極小的正數,可取為障礙常數μ與全1列向量e的乘積。引入障礙函數項,則原問題的優化目標函數式轉化為:
當松弛變量u、l、s靠近邊界時,上式將趨于無窮大,因此滿足極小值不會在邊界上取得。綜上可得到僅含等式約束的優化問題,其包含互補約束的拉格朗日函數為:
其中:y=[y1,…,ym]T,z=[z1,…,zr]T,w=[w1,…,wr]T,為各變量對應的拉格朗日乘子。為求得原問題的極小值,對變量及乘子的偏導數均需等于零,即:
Ly=h(x)=0
Lz=g(x)-l-g=0
Lt=q(x)+s-μe=0
其中:l,u,s,z>0,w,t<0。其中L、U、Z、W、S及T分別為以向量l、u、z、w、s及t各元素為對角元構成的對角矩陣。L=diag(l1,…,lr),U=diag(u1,…,ur),Z=diag(z1,…,zr),W=diag(w1,…,wr), 由及可以得到μ=(lTz-uTw-sTt)/(2r+2ng),定義對偶間隙Gap=lTz-uTw-sTt,則μ=Gap/(2r+2ng)。為提高算法收斂性,引入中心參數σ(σ∈(0,1)),令μ=σGap/(2r+2ng),本發明中σ取0.1。
采用牛頓-拉夫遜法求解式非線性方程組,得到修正方程組:
將上式寫成矩陣形式,并通過列變換得到下式:
式中:
含變量Δx、Δy的修正方程組矩陣維數顯著減少,且其余變量可直接回代計算得到。在進行松弛變量、拉格朗日乘子、各變量初值等初始化之后進行迭代計算,各變得到的修正量不斷更新,最終得到最優解。
對于變壓器抽頭和電容電抗等離散控制變量,需要采用內嵌二次罰函數法進行處理。采用基于正曲率二次罰函數的模型來模擬離散控制的虛擬費用。同樣,這一附加于優化費用之上的虛擬費用將迫使離散控制變量靠在某一個分級上。
容易得到在b1的鄰域內的二次罰函數及其一階、二階導數為:
上式中,μi是對應于bi的正數罰子。將二次罰函數π(bi)引入到增廣的拉格朗日函數中,實際上是在解算中將其一階導數項加入右端梯度向量中,二階導數項加入到左端系數矩陣中相應的對角元上。加之變壓器變比t對應的對角元在客觀上是小主元,則兩類離散控制變量都造成了W陣的“病態”。這樣,當采用上述正曲率二次罰函數模型進行離散化處理后,隨著正數罰子μi的引入,不但離散化處理的既定目的可以達到,而且可以取代原來基于加強矩陣正定性的軟懲罰的作用,使內點法系數矩陣的正定性真正得到加強。
選擇在解算中的什么時機將二次罰函數引入的標準將有利于解算的快速正確收斂。在解算開始時就引入顯然是不利的,因為此時罰函數帶來的虛擬費用必然對全局優化的費用降低起到不適當的干擾作用;同理,等到求到一個最優解之后再引入罰函數的作法也是不好的,因為這將延緩了解算的收斂。引入的最佳時機應當有以下兩個條件被滿足:
1)最優解處起作用的電壓不等式約束集(即Binding V-Set)被基本鎖定;
2)離散控制變量的矯正量Δb需小于一個門檻值δ。
數值試驗表明,一般在第3次主迭代后,Binding V-Set能被基本鎖定。Δb的變化規律則與所采用的改善穩定性的軟懲罰策略有關系。在采用上述的改進的軟懲罰策略后,一般也在第3次主迭代后滿足要求:δ=Step/8
圖1為罰幅修正的函數圖,如圖1所示,當引入罰函數以后,變量b將可能有兩種變化趨勢:一是沿著罰函數起作用的方向靠向所屬的鄰域中心;二是沿著罰函數起作用的反方向靠向另一端。顯然,在后一種情形 下,離散罰函數的作用是消極的,應當減弱或者取消。這一現象是很常見的,而能否很好地處理這一現象則是評價一個離散化模型優劣的關鍵。采用如下線性函數來自動修正罰子的大小。先定義變量bi到其鄰域中心b1的距離bx1=|bi-b1|。則當bi在內時有:
其中,μmax,μmin分別是最大、最小離散罰子(其數值分別可取100和10)。由此產生的作用是,當離散變量bi在罰函數作用下向中心b1運動時,罰子自動增大,使其加快到達b1;當b1向相反方向運動時,罰子自動減小,而使其加快向全局最優方向運動。
圖2為本發明實施例中主配網一體化分布式最優潮流的計算流程圖,如圖2所述,在內點法最優潮流解算過程中,當第K次主迭代完成以后,按以下步驟執行。
a)判斷一階最優化條件是否已滿足。是則結束解算,否則繼續;
b)判斷離散變量是否已越上/下邊界,是則引入邊界罰函數處理,否則繼續;
c)判斷離散變量是否已引入了罰函數,是則轉e),否則繼續;
d)判斷離散罰函數引入的條件是否已滿足,即(1)迭代次數大于3;
(2)Δbi<δ=Step/8。是則繼續,否則轉步驟f;
e)計算罰子幅值;
f)引入二次罰函數,進行離散化處理;
g)繼續第K+1次主迭代,回到a)。
實施例2
本發明的步驟二:
配網的供電區內分布式電源與負荷的優化調度子問題
第i個配網智能體的供電區內分布式電源與負荷的優化調度是通過切換聯絡開關與分段開關的狀態,以恢復非故障失電區的連通,并優化連通后的潮流,實現配電網的安全穩定運行。其數學模型可寫為:
min CD,i
ΔPDR,j≤ΔPDR,j,max
其中,網絡拓撲約束,即保證重構后的配網依然為輻射狀的連通網絡,無孤島存在,ΔPDR,j,max和ΔPDR,j分別為第j個需求側響應的最大可控功率和實際調節功率值。
本發明將可控的DG作為研究對象,其數學模型表示為PQ模型。配網智能體子優化問題的目標函數為(忽略下標i):
CD,i=ω1Cldsd+ω2CDG+ω3Closs+ω4Cbal+ω5CDR+ω5Cbreaker
本式中,ω1,ω2,ω3,ω4,ω5,ω6為6個子目標的權重系數。其中,最小失負荷的目標函數Cldsd為:
式中:Nld是配電網中的負荷總數。
DG發電經濟性的目標函數為:
式中:NR是配電網中的支路總數;ri是支路i的電阻;Ii為流過支路i的電流,ki為開關i的狀態,0表示開關斷開,1表示開關閉合。
有功損耗的目標函數為:
式中:NR是配電網中的支路總數;ri是支路i的電阻;Ii為流過支路i的電流,ki為開關i的狀態,0表示開關斷開,1表示開關閉合。
負荷均衡化率的目標函數為:
式中:Si、Si,max分別表示支路i的視在功率和容量。
需求側響應的目標函數為:
式中:NDR表示配網中需求側響應的個數;cDR,j為第j個需求側響應的成本。
最小開關動作次數目標函數為:
式中:Nbreaker為配網中可控開關個數,Bj表示第j個開關的狀態,1表示動作,0表示維持原狀態。
配網優化調度子問題的求解采用分支定界-原對偶內點法求解配網層智能體優化調度子問題的關鍵在于通過分支使離散變量逐步逼近離散值,得到僅含連續變量的優化松弛子問題,采用原對偶內點法進行求解,并將不滿足約束的子問題進行剪支。
(1)分支過程
在分支前應先對所有離散變量進行分支排序。由于電容電抗投切直接改變系統的無功大小,而變壓器變比只改變系統的潮流分布,所以在分支次序上優先考慮電容電抗。又由于離散變量歸整后的變化量越大,越有可能引起解位置的變化,所以在上述基礎上優先分支偏離大的離散變量。
采用的分支方法為變元二分法,即對未取得離散值的離散變量引入界約束,形成兩個新的松弛子問題。圖3為分支方法的示意圖,如圖3所示,方法引入界約束。
圖中為離散變量xi在區間[xi,min,xi,max]上的連續解,Ii為xi的一個離散值,且但是對于聯絡開關與分段開關的狀態而言,只有0和1兩個狀態,是上述分支方法的一種特殊情況,可按照圖4所示方法進行分支,圖中為離散變量ki在區間[0,1]上的連續解。
(2)子問題的原對偶內點法求解
引入界約束后的松弛子問題中聯絡開關或者分段開關為0或者1,而變壓器變比和電容電抗補償值在其界約束內是作為連續變量進行求解的,因此松弛子問題實際上是一個僅含連續變量的優化問題。
(3)剪支過程
當采用原對偶內點法求解出松弛子問題后,需對滿足剪支準則的子問題進行剪支。優化問題中有以下4條剪支準則:1)子問題不可行;2)子問題已取得所有離散變量的整數解;3)子問題中聯絡開關或者分段開關的取值不滿足配網拓撲約束;4)子問題目標值大于等于上界值。
首先將各離散變量固定為該初值,對其進行無功優化,得到一個整數可行解。由于該整數解中各離散變量均無法調節,其質量勢必劣于算法所得優化解,因此可將該整數解作為原問題的上界。然后采用圖4所示的方法進行剪支判斷。UB為上界解中對應目標值,紅色圓點為所有變量均取得整數解且待判斷的子問題,obj(T)為其目標值。按下式進行比較:
obj-UB<0
通過剪支過程可以刪除一些不滿足配網拓撲約束條件以及在未完成所有離散變量求整前目標函數已經大于上界的子問題,減少不必要的計算。
(4)算法步驟
本發明提出的基于分支定界-原對偶內點法的優化算法步驟如下:
a)建立數學模型;
b)將離散變量值固定為初值,進行只含連續變量的優化,得到原問題上界;
c)依次對待分支隊列BP中的子問題進行分支,采用原對偶內點法求解各松弛子問題,并對是否所有離散變量取得離散值進行判斷,若是,則轉g);若否,則將其加入下次分支隊列XP中;
d)針對子問題所得解的不同情況進行如下處理:
i)若子問題中聯絡開關或分段開關取得離散值,則判斷其是否滿足配網的拓撲約束;
ii)若子問題中聯絡開關或分段開關未取得離散值,則繼續;
e)根據剪支準則對下次待分支隊列XP中的各子問題進行剪支處理。
f)用剪支后的XP更新BP。
g)判斷待分支隊列BP是否為空:若是,則從已得整數可行解中取出目標值最小的解作為最優解;否則轉至步驟d)。
在本發明的步驟三中:
主配網一體化分布式優化的具體計算,利用主、配電網最優潮流分布式交替迭代完成計算。在主網Agent中求解可得各PCC點狀態變量xpcc,并將其傳遞給各個配電網;第i個配電網(i=1,2,…,n)以為根節點狀態變量求解可得其他節點的狀態變量計算PCC點等值負荷功率和 后將其返回主網;主網收到各PCC點的等值負荷功率后重復上述步驟進行計算,直至滿足如下收斂條件:
其中,ε為收斂精度,為PCC點的電壓幅值。最終通過主、配電網間PCC點處電氣量的交換實現主配網一體化故障恢復優化控制的計算。
以上所述實施例僅表達了本發明的實施方式,其描述較為具體和詳細,但并不能因此而理解為對本發明專利范圍的限制。應當指出的是,對于本領域的普通技術人員來說,在不脫離本發明構思的前提下,還可以做出若干變形和改進,這些都屬于本發明的保護范圍。因此,本發明專利的保護范圍應以所附權利要求為準。
- 還沒有人留言評論。精彩留言會獲得點贊!