一種特大流域暴雨洪水分類及類型識別方法

本發明屬于洪水分類及識別，涉及到一種利用洪水空間組成對場次洪水劃分類型并進行識別的方法，尤其涉及一種特大流域暴雨洪水分類及類型識別方法。

背景技術：

1、洪水作為一種復雜的自然現象，既具有確定性又具有隨機性，洪水發生頻率、強度和影響范圍都可能隨著氣候變化和人類活動而發生變化，不同類型洪水的發展過程和影響范圍都有所不同（turkington?t.,?breinl?k.,?ettema?j.,?et?al.?a?new?flood?typeclassification?method?for?use?in?climate?change?impact?studies[j].?weatherand?climate?extremes,?2016,14(c),1-16.），從而影響水庫調度方式，制約著洪水資源利用效率。根據一定的原則對洪水類型進行劃分，并在調控過程中實時識別、分類調度，是認識流域洪水規律、緩解防洪興利矛盾的有效途徑，能夠在保障防洪標準的不降低的前提下，有效提高洪水資源利用潛力。

2、目前洪水分類研究主要集中于中小流域，更多的研究是根據洪水發生后的特征信息，如洪量、洪峰、洪水歷時等，基于洪水場次的共同點和差異點之間的自然分類標準，將洪水過程分成多種類型，然后應用于分類預報以提高預報精度。這些研究大多以中小流域的整場洪水過程為研究對象，以過程指標進行相似性劃分，對特大流域的洪水分類及在洪水發展過程中實時識別洪水類型的研究較少。特大流域涵蓋了廣闊的地理區域，具有流域面積大、地形類型豐富、暴雨天氣系統多、干支流水系復雜的特點。洪水受到地形特征、水庫調度、產匯流機制等多種復雜因素的影響，這些因素相互作用，使洪水的形成和發展具有高度復雜性，使得干支流水系在同一出口斷面的流量過程差異明顯，僅依賴洪水過程指標進行洪水分類，洪水間相似性偏低，將產生大量離散點。然而，同一出口斷面場次洪水組成的總體格局相似，依據各干支流洪水組成差異進行分類，可以有效劃分洪水類型并區分主來水區。

3、洪水分類主要有三種方法，分別為成因分析法、智能優化法和聚類分析法。成因分析法從洪水的物理成因入手，研究其相關規律，把具有相似性特征的洪水分為一類，能夠將復雜的問題分解成更小的部分，具有直觀性強的優點，但成因分析需要依賴專家的經驗和判斷，具有一定的主觀性；智能優化算法包括人工神經網絡算法、人工蜂群算法、混合蛙跳算法等，解決了洪水分類過程的魯棒性問題，具有高效性和全局搜素能力（陳春梅,王正元,屈娜.人工智能優化算法綜述[j].大學,2020,(26):71-72.），常被廣大學者用來優化算法以提高分類精度，但需要根據具體問題的特性選擇合適的智能優化算法，如果選擇不當可能導致效果不佳；聚類分析法基于統計學理論，應用普通數學方法或者模糊數學方法，利用數據本身的特征進行分析，能夠在不需要先驗知識的情況下找到數據中的結構和模式進行聚類。聚類算法簡單、易于理解、可操作性強，對于該算法存在對初始參數及數據異常值敏感的問題，可以通過算法優化和數據審查的方式進行改善，梁宇生等（梁宇生，楊曉芳，胡丹.模糊聚類分析在水文預報中的研究及應用[j].數學學習與研究，2018(19),149.）在曹娥江流域運用加權模糊c均值聚類算法進行洪水分類時提前采用isodata?聚類算法確定聚類數。因此聚類?算法逐步成為洪水分類領域中行之有效的主流方法，dinesh（dinesh?s..fuzzy?classification?of?simulated?droughts?and?floods?of?water?bodies[j].journal?of?applied?sciences,?2007,?7(18):?2610-2616.）通過模糊聚類對多個流域的歷史洪水過程進行分類，證明了該方法在不同流域中的良好適用性。目前洪水分類上主要以系統聚類、k-means聚類和模糊聚類為主。

4、洪水識別則是通過獲得的相關降雨、洪水等信息，結合流域已有的長期歷史洪水數據，檢索與當前洪水相似的歷史洪水過程或洪水類型。目前的洪水識別研究多集中于使用洪水發生后的特征信息進行識別，對于如何提前識別洪水類型的研究較少。暴雨洪水指的是由于短時間內強降雨引起的洪水現象，洪水形成過程與高強度降雨的形成和發展息息相關，因此以洪水的主要成因（即暴雨量）為先驗識別指標，提前識別即將發生洪水的類型，能夠根據歷史上相似的洪水提供的信息預測未來洪水的有關特征，或參考歷史上相似洪水的處理方案構建未來洪水的處理方案。

5、以下對生物辨識智能卡模塊研究及數據預測研究領域的進行闡述：

6、在生物辨識智能卡模塊的研究領域，現有的模塊通常結合了接觸和非接觸的通信接口，不僅僅用于身份驗證，還能支持財務交易、訪問控制等多種功能，設計實現了多種智能卡功能的集成，能滿足多種應用需要。隨著技術的進步和對用戶體驗的重視，生物辨識模塊越來越多地被集成到智能卡中，同時模塊的厚度和體積被設計得更小，減少了模塊的尺寸和復雜性，提高了安裝的便捷性，保障了用戶便利。隨著社會發展，電子支付和身份驗證需求的日益增長，生物辨識智能卡的市場需求將持續上升，該方向的研究將向著更高的集成度、更強的安全性和更好的用戶體驗方向發展。

7、在數據預測領域，尤其是施工數據預測方面，機器學習算法（如支持向量機、神經網絡等）在數據預測中普遍應用，這些算法能夠處理復雜的非線性關系，并從大量歷史數據中提取有用的信息，許多預測模型現在能實時接收和處理新數據，從而動態調整預測結果，提高預測的時效性和準確性。研究者們為了進一步的提高預測準確性，探索將多種算法結合，形成混合模型以供使用，這類研究可以在優化模型參數的同時提高模型的泛化能力。值得注意的是，數據質量直接影響到預測模型的表現，因此，對數據預處理（如去噪、填補缺失值、標準化等）在整個預測過程中顯得尤為重要。

技術實現思路

1、針對現有技術的不足，本發明提供一種典型洪水分類及動態識別的方法。該方法基于場次洪水的組成特征，分別構建了以降雨及洪水為分類指標的場次洪水分類方式，驗證了利用降雨信息識別洪水類型的可能性及準確性，并最終于實時調度運行中應用降雨信息對洪水類型進行動態識別。該分類及識別方法充分考慮了洪水地區組成差異較大的問題，能夠提前確定洪水類型，為水庫調度決策提供決策依據。

2、為了達到上述目的，本發明采用的技術方案如下：

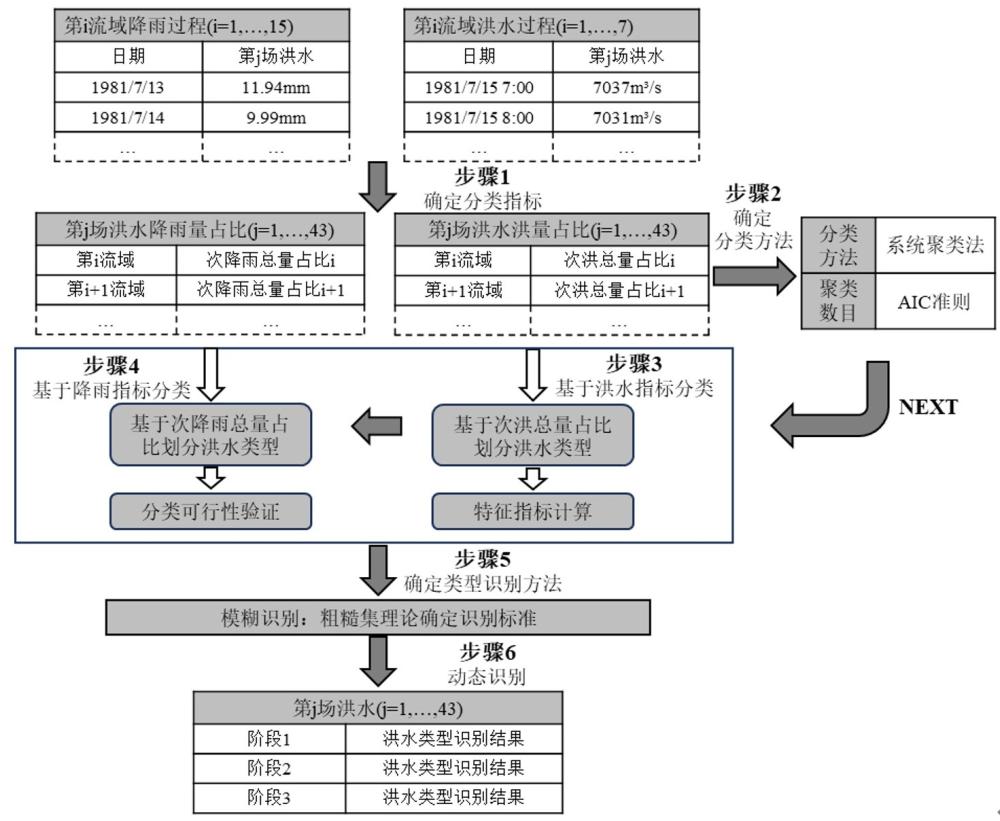
3、一種特大流域暴雨洪水分類及類型識別方法，所述識別方法首先，確定并計算用于分類的降雨及洪水相關指標；其次，基于洪水分類指標對場次洪水進行分類并解析各類洪水過程的形態、速率、強度特征；再次，基于降雨指標對場次洪水進行分類并驗證利用降雨信息分類的可行性及準確性；最后，根據場次洪水分類結果生成基于降雨信息的決策規則并分三個階段進行洪水類型動態識別。場次洪水分類及識別流程示意圖如附圖1所示。包括以下步驟：

4、第一步，確定并計算分類使用的降雨及洪水相關指標；

5、結合特大流域面積大、支流及區間多、來水過程復雜的特點，以洪水組成作為分類指標進行分類。本發明所述的分類指標包括洪水分類指標和降雨分類指標兩種。

6、采用次洪總量占比作為洪水分類指標，該洪水分類指標計算如公式（1）所示，

7、?；（1）

8、其中，是第個流域在第場洪水的洪水總量占比，是第子流域，是第場洪水；是第個子流域在第場洪水中匯入控制斷面的洪量；是第場洪水出口斷面的總洪量。

9、采用次降雨總量占比作為降雨分類指標，該降雨分類指標計算如公式（2）所示，

10、?；（2）

11、其中，是第個分區在第場洪水的累計次降雨總量占比，是第分區；是第個分區在第場洪水的總降雨深；是第分區的流域面積。

12、其中，使用次洪總量占比和次降雨總量占比兩個指標進行分類的過程是相互獨立。

13、第二步，基于次洪總量占比對洪水進行分類；

14、步驟2.1）本發明以場次洪水為樣本，采用系統聚類法，利用樣本之間距離最近原則，對場次洪水進行類型劃分；

15、首先，在步驟2.1）中，?涉及到分類數量的確定，以明確最佳分類數。本發明采用aic（赤池信息）準則判定場次洪水應分為幾種類型最合理。aic指數計算如公式（3）所示，

16、?；(3)

17、其中，aic是判斷最佳分類數的指數，最小aic值對應為最佳分類數；是通過系統聚類得到的類型數目；是分類結果的對數似然函數的最大值；l是似然函數。

18、進一步的，所述步驟2.1）中基于系統聚類法劃分場次洪水類型的過程如下所示：

19、（2.1.1）采用歐式距離計算各場次洪水之間的距離。計算如公式（4）所示，

20、<mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>d</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mrow><mi>jj</mi><mi>'</mi></mrow></msub></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>=</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mo>[</mo><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true"><munderover><mo>∑</mo><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>k</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>=</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mn>1</mn></mstyle></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>b</mi></mstyle></mstyle></munderover><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mo>(</mo><mstyle displaystyle="true" mathcolor="#000000"><mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mrow><mstyle displaystyle="true" mathcolor="#000000"><mi>j</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>k</mi></mstyle></mrow></msub></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>?</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>x</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msub><mrow /><mrow><mstyle displaystyle="true" mathcolor="#000000"><mi>j</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>'</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>k</mi></mstyle></mrow></msub></mstyle></mstyle><mo>)</mo></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msup><mrow /><mstyle displaystyle="true" mathcolor="#000000"><mn>2</mn></mstyle></msup></mstyle></mstyle></mstyle></mstyle></mstyle><mo>]</mo></mstyle><mstyle displaystyle="true" mathcolor="#000000"><msup><mrow /><mrow><mstyle displaystyle="true" mathcolor="#000000"><mn>1</mn></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>/</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mn>2</mn></mstyle></mrow></msup></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>(</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>j</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>=</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mn>1</mn></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mn>2</mn></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>.</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>.</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>.</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>c</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>j</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>'</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>=</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mn>1</mn></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mn>2</mn></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>?</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>,</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>c</mi></mstyle><mstyle displaystyle="true" mathcolor="#000000"><mi>)</mi></mstyle></mstyle>?；(4)

21、其中，是第、兩場洪水間的歐式距離；是第場洪水的第個指標；是第場洪水的第個指標；是洪水分類指標總數。

22、通過計算場次洪水間的歐式距離得到距離矩陣：

23、；?(5)

24、（2.1.2）采用類平均距離計算各種類型洪水間的距離。計算如公式（6）和公式（7）所示，

25、；?(6)

26、其中，定義是第類洪水，是第類洪水；是兩類洪水距離的平均；和分別是類和類中的洪水樣本數；表示類中的樣本，表示類中的樣本；定義為任意一類洪水，為兩類洪水合并后的新洪水類型；當和合并為的時候，任意一類洪水與的距離為：

27、；?(7)

28、其中，是和的距離；是和的距離；是類中的洪水樣本數。

29、（2.1.3）根據公式（5）計算得到的整個流域內的任意兩場洪水間的距離，取其中距離最小的兩兩場洪水合并為一類洪水；根據公式（6）計算得到的各類洪水間的距離，合并距離最近的兩類洪水成新的洪水類型；再根據公示（7）計算任意一類洪水與新洪水類型的距離；然后返回步驟(2.1.2)，如此循環，直至各場洪水合并為最佳aic指數對應的類型數。

30、步驟2.2）根據第一步確定的洪水分類指標（次洪總量占比）和步驟2.1）的分類方法，對各場次洪水進行分類得到四種類型的洪水。所述的四種類型的洪水具體為岷沱江及嘉陵江遭遇型、烏江及干流區間遭遇型、嘉陵江型、嘉陵江及寸三區間遭遇型。

31、步驟2.3）基于步驟2.2）得到的場次洪水分類結果，進行四種類型洪水的特征解析，其中，不同類型洪水在形態、流量過程等方面存在差異，故選擇每種類型洪水的形態指標、速率指標、強度指標分析各類型洪水的特征。

32、進一步的，所述步驟2.3）中形態指標、速率指標、強度指標包含的具體指標及其計算如下所示：

33、所述形態指標有洪峰時間偏度、流量變差系數、高脈沖歷時占比，計算如公式（8）-公式（10）所示，

34、?；?(8)

35、其中，是洪峰時間偏度，是漲洪歷時，是洪水總歷時。反映了場場次洪水中洪峰出現的相對時間，取值越小，表明洪峰出現時刻越靠前。

36、<mstyle displaystyle="true" mathcolor="#000000"><mi>cv</mi><mi>=</mi><mfrac><mrow><mi>σ</mi><mrow><mo>[</mo><mrow><mi>q</mi><mrow><mo>(</mo><mi>t</mi><mo>)</mo></mrow></mrow><mo>]</mo></mrow></mrow><msub><mi>q</mi><mi>av</mi></msub></mfrac></mstyle>?；(9)

37、其中，是流量變差系數，是場次洪水過程，<mstyle displaystyle="true" mathcolor="#000000"><mi>σ</mi><mrow><mo>[</mo><mrow><mi>q</mi><mrow><mo>(</mo><mi>t</mi><mo>)</mo></mrow></mrow><mo>]</mo></mrow></mstyle>是次洪過程標準差，是次洪過程的平均流量。取值越大，表明洪水過程越陡峭、尖瘦。

38、；?(10)

39、其中，是高脈沖歷時占比，是流量值大于75%洪峰流量值的洪水過程的持續時間。取值越大，表明洪峰形態越寬，高水量洪水過程持續時間越長。

40、所述速率指標有漲洪速率、落洪速率，計算如公式（11）和公式（12）所示，

41、?；(11)

42、其中，是漲洪速率，和分別是次洪洪峰流量和起漲流量，是洪水起漲時刻，是洪峰出現時刻。取值越大，表明洪水起漲速度越快，易在短時間內形成災害性洪水。

43、?；(12)

44、其中，是落洪速率，是次洪終止流量，是洪水終止時刻。

45、所述強度特征指標有洪水總量和洪峰流量。

46、每一類型的洪水通過公式（8）-（12）得到形態指標3種、速率指標2種、強度指標2種。

47、步驟2.4）比對步驟2.3）得到的每一類型洪水的7種指標與歷史洪水的特征描述，若不同類型的典型洪水與歷史特征描述相符，則認為分類合理，得到分類結果準確的結論；若不同類型的典型洪水與歷史特征描述不相符，則認為分類與實際不符，洪水分類結果不適用于后續的洪水類型識別工作，應返回第一步，調整洪水分類指標、分類方法等，重新劃分場次洪水類型。

48、第三步，基于次降雨總量占比對洪水進行分類；

49、步驟3.1）本發明以場次洪水對應的場次降雨為樣本，采用系統聚類法，利用樣本之間距離最近原則，對場次降雨進行類型劃分；所述步驟3.1）中基于系統聚類法劃分場次洪水類型的過程與步驟2.1）保持一致；

50、步驟3.2）根據第一步確定的降雨分類指標（次降雨總量占比）和步驟3.1）的分類方法，對各場次洪水對應的場次降雨進行分類得到四種類型的洪水。所述的四種類型的洪水具體為岷沱江及嘉陵江遭遇型、烏江及干流區間遭遇型、嘉陵江型、嘉陵江及寸三區間遭遇型。

51、第四步，對第二步和第三步洪水分類結果進行可行性驗證；

52、若第二步得到的基于次洪總量占比的準確分類結果與第三步得到的基于次降雨總量占比的分類結果重疊度達到85%及以上，認為第三步基于降雨指標（次降雨總量占比）分類是可行的，應繼續進行第五步的洪水類型識別工作；反之則認為不可使用次降雨總量占比為洪水分類、識別的判別指標，應重新選擇指標、重新分類、重新進行可行性驗證。

53、第五步：確定用于洪水類型識別的方法；

54、在進行洪水類型識別時，指標較多且不同類型的洪水之間界限不明確，模糊邏輯提供了一種處理不確定性和模糊性的有效工具，適合于處理洪水事件中具有不同類型特征的數據。本發明采用模糊識別中的粗糙集理論，挖掘分類指標與洪水類型間的隱含關系，確定對洪水類型進行識別的決策規則，并分為三個階段對洪水的類型進行識別。

55、所述的應用粗糙集理論對洪水類型進行識別的過程如下所示：

56、步驟5.1）屬性選擇與簡約；

57、利用粗糙集理論的屬性約簡方法，計算降雨分類指標的屬性重要度去除冗余屬性，求得降雨分類指標的核屬性，提取出對于不同洪水類型最具決策性的次降雨總量占比，重要度越大說明該次降雨總量占比對分類的能力越強。

58、步驟5.2）確定下近似和上近似；

59、基于步驟5.1）提取的最具決策性的次降雨總量占比，計算每種洪水類型的下近似和上近似，確定每種洪水類型的典型特征和邊界。其中，下近似是指包含所有可能被歸類為某一洪水類型的樣本的最小集合；上近似是指排除所有不可能被歸類為某一洪水類型的樣本后的最大集合。

60、步驟5.3）確定決策規則；

61、基于步驟5.2）確定的下近似和上近似，推導出用于識別洪水類型的決策規則。

62、步驟5.4）應用和實施；

63、基于步驟5.3）確定的決策規則，分三個階段識別實際的場次洪水過程所對應的洪水類型。

64、進一步的，步驟5.4）所述的洪水識別的三個階段如下所示：

65、階段1：尚未產生落地雨，完全利用預報降雨信息進行洪水類型識別；

66、階段2：降雨不斷發展，由于每個類型洪水的主降雨區不低于兩個，因此在前期存在高強度降雨區域的子流域不高于兩個時，結合實測降雨和后續的降雨預報信息（該專利使用的預報產品為ecmwf），對洪水類型進行識別；

67、階段3：各區域高強度降雨已生成，降雨強度減小，此時結合實測降雨和預報降雨信息，對洪水進行識別，不同場次洪水的該節點的時間區間存在差別。

68、第六步：基于降雨信息進行洪水類型動態識別；

69、根據第五步確定的洪水類型識別的決策規則，結合預報降雨信息（該專利使用的預報信息是歐洲中期天氣預報中心(ecmwf)的預報降雨數據）和落地雨信息，對場次洪水過程所屬的洪水類型進行動態識別。

70、與現有技術相比，本發明具有以下優點和效果：

71、本發明給出了基于組成的分類方式，確定了識別的決策規則，提出了利用降雨信息對洪水類型進行動態識別的方法。根據以上過程，該方法分別使用次洪總量占比和次降雨總量占比進行分類，使用預報降雨和落地雨進行洪水類型的動態識別，因此該識別方法能夠在洪水發生發展中分段識別類型，具有實時性的優點，能夠提前判斷，輔助提早決策。