一種基于凍融貝葉斯優化技術的模擬電路成品率優化方法

本發明屬于集成電路可制造性設計，涉及集成電路可制造性設計中模擬電路成品率優化，具體涉及一種基于凍融貝葉斯優化技術的模擬電路成品率優化方法。本方法明顯優于現有技術方法，能大幅減少模擬電路成品率優化所需仿真次數。

背景技術：

1、現有技術公開了隨著半導體制造工藝特征尺寸縮小至納米尺度，工藝擾動對模擬電路的性能、成品率產生了很大影響。為了應對模擬電路設計中日益嚴峻的可靠性挑戰，工業界近來越來越關注模擬電路成品率優化問題[1]。一般而言，模擬電路成品率優化采用迭代優化循環，在每一次迭代優化步驟中，設計人員需調整設計參數，如晶體管尺寸等，然后執行耗時的成品率分析。由于成品率分析(工藝角或蒙特卡洛仿真)需要執行約上千次仿真才能保證分析結果準確，因此整個模擬電路成品率優化的時間成本極高。考慮到產品上市時間日益縮短，減少模擬電路成品率優化的整體仿真時間成為最迫切需求。

2、現有技術中，關于模擬電路成品率優化問題，目前主要的方法包括以下三類。

3、基于工藝角的方法[2]-[4]，該方法優化給定模擬電路在幾個工藝角下的“最差”性能。盡管這種處理方式避免了代價高昂的成品率分析過程，但它們的優化結果精度不高，且經常導致過度設計。此外，若工藝空間維度很高，這種方法搜索“最差”性能的代價高昂。

4、基于蒙特卡洛(monte?carlo，mc)的方法，由于其高精度和通用性被廣泛使用。文獻[5，6]將最佳計算預算分配(optimal?computational?budget?allocation，ocba)技術應用于mc加速，利用進化算法進行優化問題求解。文獻[7]采用核密度估計方法進行成品率建模，并提出了一種多起點期望最大化算法來解決該問題。文獻[8]提出了一種自適應成品率分析方法，并利用基于加權期望提升函數的貝葉斯優化算法尋找最優設計。文獻[9]在文獻[8]的基礎上進一步采用結合神經網絡的高斯過程回歸和最大值熵搜索方法進行優化。盡管貝葉斯優化方法在之前的研究中已經顯示出一定的優勢，但所需的總仿真次數過多。例如，目前最先進的方法[8]和[9]一次成品率優化需要600020000次仿真，這對于稍大規模的模擬電路而言，在時間上是難以接受的。

5、基于代理模型(surrogate?model)的方法，文獻[10]試圖建立一個電路性能的代理模型來代替昂貴的電路仿真，從而降低成品率優化的成本。然而，這些方法往往需要大量的仿真樣本點來保證建模的準確性，并且建模所需的樣本點數量隨工藝空間維度指數增長[8]，因此在finfet先進工藝下建模的難度極大。

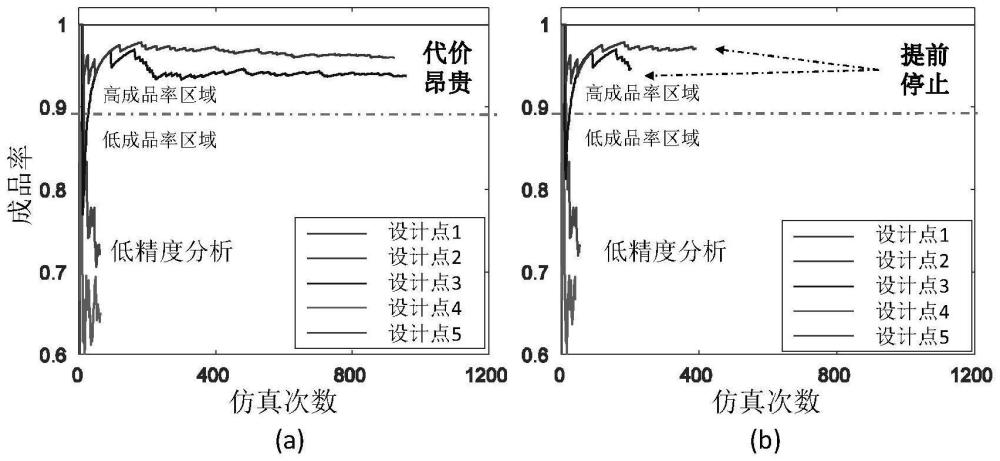
6、事實上，模擬電路成品率分析可以設置不同的分析精度，并且對于不同成品率設計點應當執行不同精度的成品率分析，例如在文獻[8]中，對低成品率設計點執行低精度成品率分析，以節省仿真資源。如圖1所示，其中x軸是仿真次數，y軸是成品率，不同的曲線對應不同的設計點。圖1(a)為文獻[8]的傳統貝葉斯優化方法，圖1(b)為本發明提出的凍融貝葉斯優化方法。在圖1(a)中，低成品率設計點4和5只進行低精度的成品率分析以節省仿真次數，但對于高成品率的設計點，例如設計點2和3，文獻[8]必須執行高精度成品率分析來區分它們，產生巨大的仿真成本。為了克服上述問題，凍融貝葉斯優化的基本思想是：收集潛在高成品率設計點并逐步提高其成品率分析精度，而不是立即執行高精度成品率分析。一旦找到更高成品率的設計點，那些收集的潛在高成品率設計點的分析過程就可以提前終止。這就是凍融貝葉斯優化方法能夠提升優化效率的原因。如圖1(b)所示，由于找到更高成品率設計點1，被臨時凍結的高成品率設計點2和3的成品率分析過程可提前終止。

7、針對現有模擬電路成品率優化方法中優化效率低的問題，本技術擬提出一種基于凍融貝葉斯優化技術的模擬電路成品率優化方法。本方法較現有技術方法，能大幅減少模擬電路成品率優化所需仿真次數。

8、與本發明相關的現有技術有，

9、[1]g.gielen，t.eeckelaert，e.martens，and?t.mcconaghy,“automatedsynthesis?of?complex?analog?circuits，”in?european?conference?on?circuittheory?and?design，2007

10、[2]r.schwencker,f.schenkel，m.pronath，and?h.graeb，“analog?circuitsizing?using?adaptive?worst-case?parameter?sets，”in?proc.date，2002.

11、[3]m.barros，j.guilherme，and?n.horta，“analog?circuits?optimizationbased?on?evolutionary?computation?techniques，”integration，the?vlsi?journal，2010.

12、[4]m.sengupta，s.saxena，l.daldoss，g.kramer,s.minehane，and?j.cheng，“application-specific?worst?case?corners?using?response?surfaces?andstatistical?models,”ieee?tcad,2005

13、[5]b.liu，f.v.fernandez，and?g.g.gielen，“efficient?and?accuratestatistical?analog?yield?optimization?and?variation-aware?circuit?sizingbased?on?computational?intelligence?techniques，”ieee?tcad，2011.

14、[6]i.guerra-gomez，e.tlelo-cuautle，and?l.g?de?1a?fraga，“ocba?in?theyieldoptimization?of?analog?integrated?circuits?by?evolutionary?algorithms，”in?proc.iscas，2015

15、[7]m.wang，f.yang，c.yan，x.zeng，and?x.hu，“efficient?bayesian?yieldoptimization?approach?for?analog?and?sram?circuits，”in?proc.dac，2017.

16、[8]m.wang，w.lv，f.yang，c.yan，w.cai，d.zhou，and?x.zeng，“efficient?yieldoptimization?for?analog?and?sram?circuits?via?gaussian?process?regression?andadaptive?yield?estimation，”ieee?tcad，2018.

17、[9]s.zhang，f.yang，d.zhou，and?x.zeng，“bayesian?methods?for?the?yieldoptimization?of?analog?and?sram?circuits，”in?proc.aspdac，2020.

18、[10]s.basu，b.kommineni，and?r.vemuri，“variation-aware?macromodelingand?synthesis?of?analog?cireuits?using?spline?center?and?range?method?anddynamically?reduced?design?space，”in?proc.vlsidesign，2009.

19、[11]b.liu，d.zhao，p.reynaert，and?g?g.e.gielen，“gaspad：a?general?andefficient?mm-wave?integrated?circuit?synthesis?method?based?on?surrogatemodel?assisted?evolutionary?algorithm，”ieee?tcad，2014

20、[12]w.lyu，p.xue，f.yang，c.yan，z.hong，x.zeng，and?d.zhou，“an?efficientbayesian?optimization?approach?for?automated?optimization?of?analogcircuits.”ieee?tcas?i，2017.

21、[13]c.k.williamis?and?c.e.rasmussen，gaussian?processes?for?machinelearning.mit?press?cambridge，ma，2006，vo1.2，no.3.

22、[14]k.swersky，j.snoek，and?r.p.adams，“freeze-thaw?bayesianoptimization，”arxiv?preprint，2014.

23、[15]m.schonlau，w.j.welch，and?d.r.jones，“global?versus?local?search?inconstrained?optimization?of?computer?models，”lecture?notes-monograph?series，1998

24、[16]j.nocedal，and?s.wright，numerical?optimization.springer?science&business?media.2006

25、[17]p.hennig?and?c.jschuler，“entropy?search?for?information-effficient?global?optimization，”journal?of?machine?learning?research,2012。

技術實現思路

1、本發明的目的在于針對現有模擬電路成品率優化方法中優化效率低的問題，提出一種模擬電路成品率優化方法。具體涉及一種基于凍融貝葉斯優化技術的模擬電路成品率優化方法。本方法較現有技術方法，能大幅減少模擬電路成品率優化所需仿真次數。

2、本發明將模擬電路成品率優化問題建模為帶約束的單目標優化問題；通過求解模擬電路tt工藝角下性能優化問題，搜索剛好滿足性能約束的設計點，并將這些點作為凍融貝葉斯優化熱啟動的初始點；采用凍融高斯過程回歸方法對成品率建模并預測漸進成品率；采用結合加權期望提升函數(wei)和熵搜索函數(es)兩種獲取函數的貝葉斯優化方法，平衡優化過程中的利用和探索，對漸進成品率進行優化，不斷迭代直到成品率滿足要求或達到最大迭代次數。

3、本發明中，

4、首先，為了提升不同設計點仿真資源分配的效率，利用凍融技術，在模擬電路成品率優化的迭代循環中，對某個模擬電路設計點的成品率分析不是一次性完成，而是逐漸提高其分析精度。

5、其次，為了提高成品率預測的準確性，采用凍融高斯過程回歸方法對成品率建模并預測漸進成品率，并提出利用加權期望提升函數(wei)和熵搜索函數(es)的貝葉斯優化方法，平衡優化過程中的利用和探索，對漸進成品率進行優化，逐漸提升工藝空間中成品率分析的準確性。

6、第三，為了利用模擬電路tt工藝角性能和成品率的相關性，利用模擬電路性能優化問題求解技術，搜索剛好滿足性能約束的設計點，將獲得的設計點作為先驗知識加入模型訓練集中，可以提高建模和優化效率。

7、本發明的方法有效利用了貝葉斯優化方法采樣效率高的優勢和凍融技術的靈活性，大幅降低所需仿真時間，相比現有技術的方法，在不降低優化精度的條件下，仿真時間加速比為247～573倍。

8、具體的，本發明一種基于凍融貝葉斯優化技術的模擬電路成品率優化方法，其流程圖如圖2所示，其包括，

9、輸入參數：

10、1.模擬電路網表；

11、2.工藝參數的概率分布密度函數；

12、3.電路性能指標的失效閾值ci，i＝1，...，k，其中k為關心的電路性能指標的數量，并假設對第i個性能yi，如果仿真結果yi≥ci則認為電路成功，否則為失敗；

13、4.凍融高斯過程模型的初始數據集的點數ninit；凍融貝葉斯優化的最大迭代次數nmax；最優成品率候選集大小nb；調用模擬電路性能優化解法器的最大仿真次數npre；成品率分析時每批仿真點數目nbatch。

14、輸出結果：

15、模擬電路成品率優化得到的最優設計參數和成品率值。

16、更具體的，具體步驟包括：

17、步驟1：將模擬電路成品率優化問題建模為帶約束的單目標優化問題；

18、步驟2：通過求解模擬電路tt工藝角下性能優化問題，迭代搜索剛好滿足性能約束的設計點，并選擇其中ninit個設計點作為凍融貝葉斯優化熱啟動的初始點；

19、步驟3：對步驟2得到的ninit個初始設計點執行低精度成品率分析，建立初始數據集；并選擇其中概率意義下成品率最高的nb個點，加入最優成品率候選集b(basket)；

20、步驟4：采用凍融高斯過程回歸方法對成品率建模并預測漸進成品率；

21、步驟5：采用加權期望提升函數(wei)和熵搜索函數(es)作為獲取函數的貝葉斯優化方法，對漸進成品率進行優化，不斷迭代直到成品率滿足要求或達到最大迭代次數nmax，最終得到最優設計參數和相應的成品率結果。

22、本發明步驟1中，本發明提出將模擬電路成品率優化問題建模為帶約束的單目標優化問題。

23、對于模擬電路而言，設計參數是指晶體管的長、寬、電容值、電阻值等可由電路設計師控制的變量。工藝參數是指由芯片制造廠提供的閾值電壓等表征工藝擾動的變量。本專利涉及的成品率是指由工藝擾動產生的成品率。

24、針對一個模擬電路，設計參數x是設計空間d中的dx維向量，表示晶體管的長寬等可由電路設計師控制的變量。工藝參數s是工藝空間v中的ds維向量，表示閾值電壓等變量，其概率分布通常由工藝廠商提供，且滿足正態分布。不失一般性假設，工藝參數彼此獨立并且和設計參數無關，s的概率密度函數(probabilityden?sity?function，pdf)為

25、

26、給定設計參數和工藝參數(x，s)∈(d，v)，x∈d，s∈v，通過spice仿真可以獲得關心的電路性能y＝[y1，y2，…，yk]t，相應的閾值條件c＝[c1，c2，…，ck]t由設計師確定。只有當電路性能滿足所有的條件時，即yi≥ci，i＝1，…，k，才認為它是合格的，否則認為它失效。給定設計參數x，模擬電路成品率y(x)定義為

27、y(x)＝∫vi(x，s)p(s)ds??(2)

28、其中，指標函數i(x，s)＝and(yi≥ci)，i＝1，…，k，and(·)表示邏輯函數and。

29、模擬電路成品率優化問題是要找到具有最大成品率y的設計點x*，即

30、

31、實踐中，一個合理的模擬電路設計應當保證該電路在tt工藝角下滿足所有性能指標。通過添加這個約束，可以減小算法的搜索空間，提升收斂速度。因此，模擬電路成品率優化問題可形式化定義為：

32、

33、其中yi(x，tt)為待優化模擬電路在tt工藝角下設計參數為x時的第i個性能值。

34、本發明步驟2中，本發明提出通過求解模擬電路tt工藝角下性能優化問題，迭代搜索剛好滿足性能約束的設計點，并選擇其中ninit個設計點作為凍融貝葉斯優化熱啟動的初始點。具體包括以下子步驟：

35、步驟21：根據模擬電路成品率和tt工藝角下性能的折衷關系，將模擬電路成品率優化初始解的構造，轉化為模擬電路tt工藝角下性能優化問題。

36、由于模擬電路tt工藝角下性能優化的代價遠小于成品率優化，例如模擬電路一次性能優化一般僅需要幾百次仿真[11，12]，而一次成品率優化往往需要幾千至幾萬次仿真，因此應當從模擬電路性能優化中挖掘隱藏的知識，用以指導成品率優化。

37、圖6是一個比較器電路，它的成品率和tt工藝角下性能的關系如圖3所示，其中d1軸是比較器電路中晶體管m17的寬度，左邊縱坐標是比較器電路的成品率，右邊縱坐標是-voff，其中voff是在30℃下具有200mhz采樣頻率的失調電壓，其失效閾值為voff≤30mv。從圖3可以看出，具有最佳性能voff的設計點并不是成品率最優點，相反，那些恰好滿足性能約束的設計點可能具有更優的成品率，如d1＝8的設計點。

38、因此基于模擬電路成品率和tt工藝角下性能的折衷關系，本發明將模擬電路成品率優化初始解的構造，轉化為模擬電路tt工藝角下性能優化問題：

39、

40、其中該公式含義是搜索性能略大于約束閾值的設計點，ωi是給定的權重，代表第i個性能指標的重要性。∈是一個常系數，用于衡量tt工藝角下標稱性能yi(x，tt)與閾值ci之間的距離。本發明根據經驗設置ωi＝1，i∈1..k和

41、步驟22：采用文獻[12]提出的加權期望提升貝葉斯優化算法weibo求解步驟2.1定義的模擬電路tt工藝角下性能優化問題，記錄所有迭代優化中產生的設計點。

42、文獻[12]提出的weib?o(weighted?expected?improvement?basedbayesianoptimization)方法主要包含兩個部分：高斯過程(gaussian?process，gp)模型[13]和加權期望提升函數。在每次迭代中，利用當前的訓練數據構建高斯過程模型，然后基于該概率模型預測的后驗分布計算加權期望提升函數。通過最大化獲取函數，該方法旨在平衡利用和探索之間的權衡，即下一個采樣設計位于模型預測成品率高(利用)和/或模型預測不確定性大(探索)的地方。在對該設計進行仿真獲得其電路性能值后，將這個新樣本加入數據集。反復執行這些步驟，直到達到設置的性能優化解法器的最大迭代次數npre，記錄所有迭代優化中產生的設計點。

43、步驟23：從步驟2.2迭代優化產生的設計點中，選擇標稱性能滿足失效閾值并且具有最小f(x)值的ninit個點，作為凍融貝葉斯優化熱啟動的初始點。

44、本發明步驟3中，對步驟2得到的ninit個初始設計點執行低精度成品率分析，建立初始數據集：并選擇其中概率意義下成品率最高的nb個點，加入最優成品率候選集b(basket)。

45、本發明針對步驟2得到的ninit個初始設計點xinit，采用通用性強的mc方法，分配nbatch采樣點，執行低精度成品率分析，獲得相應的低精度成品率值，建立初始數據集。mc方法基于s的概率密度函數p(s)在工藝空間采n個樣本點si，i＝1，…，n，通過統計其中合格樣本的數量，計算成品率為

46、

47、成品率估計的方差與估計值ymc(x)和采樣點數n的關系為：

48、

49、其中置信水平kγ為常數。例如，kγ＝1.645對應90％的置信度。

50、從上述初始數據集x＝xinit中，選出nb個概率意義下成品率最高的設計點加入最優成品率候選集b中。具體選擇的標準為：

51、

52、本發明步驟4中，本發明采用凍融高斯過程回歸方法對成品率建模并預測漸進成品率。

53、傳統高斯過程模型[13]是一種非參數化概率模型，它在成品率y上定義了一個聯合高斯分布：

54、

55、其中μ為均值向量，一般取0，σ為協方差矩陣，矩陣元素由核函數k(xi，xj)決定。gp模型的核函數通常使用徑向基核函數(radial?basis?function，rbf)或matern-5/2核函數，本專利使用的核函數為matern-5/2核函數，其形式如下：

56、

57、其中xi，xj為設計空間中兩個設計點，r2＝(xi-xj)tλ-1(xi-xj)，λ＝diag(l1，…，ln)，li，i∈1..n，n為建模的點數，σf和li均為模型的超參數，可以通過極大似然法求得，即可得到一個確定的gp模型。

58、對于一個確定的gp模型和當前數據集{x，y}，x＝{xi，i＝1，…，n}，該模型能夠預測一個新設計點x0成品率的后驗均值μ(x0)和方差σ2(x0)為：

59、

60、其中k(x0，x)＝[k(x0，x1)，k(x0，x2)，…，k(x0，xn)]t。

61、對模擬電路成品率優化而言，優化過程中需要反復凋用成品率分析，因此降低成品率分析成本是提高算法整體效率的重要途徑之一。事實上，模擬電路成品率分析可以設置不同的分析精度，并且對于不同成品率設計點應當執行不同精度的成品率分析。本發明提出利用凍融技術，在模擬電路成品率優化的迭代循環中，對某個模擬電路設計點的成品率分析不是一次性調用高精度的成品率分析，而是逐漸提高其分析精度。具體來說，當第一次選中某個設計點時，我們為其分配一批少量的仿真點數，對其進行粗糙成品率分析。如果該設計點以后再次被選中，我們將添加更多批次的仿真樣本以逐漸提高其成品率分析精度。由于本發明采用的分析方法基于mc采樣，隨著仿真樣本數量增加，估算的成品率逐漸收斂。為了預測該成品率最終收斂的結果，即漸進成品率，我們采用凍融高斯過程回歸方法對成品率建模并預測漸進成品率。

62、給定當前數據集中的設計點集表示為設計點xi分配j批仿真點后計算得到的成品率值，表示在設計點xi采樣的批次數。是一個ti維矢量，代表一條針對設計點xi的成品率分析精度不斷提高的曲線，ti＝[1，…，ti]對應gi的相應采樣序列。為了對每條分析曲線建立相應的代理模型，本發明使用了文獻[14]中提出的凍融貝葉斯優化思想，采用了其定義的針對收斂曲線建模的核函數即對于有：

63、

64、其中α和β是兩個超參數。當或很大時，的值將趨于常數。

65、模擬電路成品率的凍融高斯過程建模和漸進成品率預測的方法如下：

66、首先，針對每個設計點xi，對其成品率分析精度不斷提高的曲線gi建立一個獨立的高斯過程模型：

67、

68、其中yi表示設計點xi的漸進成品率，由公式(14)定義；1i表示元素均為1的列向量；矩陣的元素值通過核函數計算得到。

69、考慮到在設計空間中，不同設計點之間成品率的相關性，漸進成品率yi被聯合建模為：

70、

71、其中y＝{y1，y2，…，yn}，先驗均值m＝[m1，m2，…，mn]是個常數向量，其元素mi是gi，i＝1，…，n的均值。矩陣kxx的元素值通過matern-5/2核函數計算得到。

72、然后，所有分析曲線的聯合分布為：

73、

74、圖4展示了凍融高斯過程回歸方法對成品率建模的基本思想。圖中每條曲線代表給定設計xi下的成品率分析曲線gi。可以看出，成品率分析過程在整個優化中以一種迭代的方式執行，而不是一次性調用高精度的成品率分析。每條曲線由建模，其中漸進成品率yi又由聯合建模，將所有分析曲線聯合起來。

75、為了訓練凍融高斯過程模型(15)，需要計算其對數似然函數，即：

76、

77、其中表示包含所有成品率分析曲線的向量。o＝blockdiag(11，12，…，1n)是一個塊對角矩陣，它的塊1i是一個長度為ti元素全為1的向量。也是一個塊對角矩陣。γ是一個n維的向量，其元素q＝dia,g(q1，…，qn)是一個對角矩陣，其元素const為常數。采用極大似然法可以獲得中的超參數α和β，以及kxx中的超參數σf和li，i∈1..n。

78、最后，利用貝葉斯推斷，可以得到當前所有設計點xi，i＝1..n的漸進成品率y的后驗分布：

79、

80、此外，對于一個新設計點xa，預測其漸進成品率y(xa)的后驗均值μ(y(xa))和方差σ2(y(xa))為：

81、

82、

83、圖5顯示了凍融高斯過程模型和傳統高斯過程模型的擬合準確度比較。橫坐標是設計空間，縱坐標是成品率。傳統高斯過程模型將當前成品率作為擬合對象，即它們試圖擬合圖中黃點a，而凍融高斯過程模型首先預測漸進成品率(例如圖中a′)，然后以漸進成品率為擬合對象預測新設計的成品率。從圖中可以看出，凍融高斯過程模型的擬合結果a′相比干傳統高斯過程模型的擬合結果a更接近真實成品率。這也驗證了本發明所采用凍融模型的有效性。

84、本發明步驟5中，采用加權期望提升函數(wei)和熵搜索函數(es)作為獲取函數的貝葉斯優化方法，對漸進成品率進行優化，不斷迭代直到成品率滿足要求或達到最大迭代次數nmax，最終得到最優設計參數和相應的成品率結果。具體包括以下子步驟：

85、步驟51：基于凍融高斯過程建模得到的模擬電路成品率模型，以模型的加權期望提升函數wei作為優化目標，建立優化問題。

86、在貝葉斯優化中，通過定義獲取函數將高斯過程概率模型提供的后驗均值和方差結合為單一的函數，并通過對獲取函數進行優化來尋找下一個可能的最優點。本發明首先采用加權期望提升函數[15]作為優化目標，指導優化過程中的利用和探索。

87、假設τ為當前找到的最優成品率，y(x)為凍融高斯過程模型預測的漸進成品率，則它相對于最優值的提升為i(y(x))＝max(0，y(x)-τ)，提升的期望為

88、ei(x)＝e[i(y(x))]＝σ(x)(λφ(λ)+φ(λ))????(20)

89、其中λ＝(τ-μ(x))/σ(x)，μ(x)和σ(x)為y(x)的后驗均值與標準差，φ(·)和φ(·)為標準正態分布的cdf和pdf函數。為了處理約束，電路性能滿足約束的概率作為ei函數的權重，得到wei獲取函數為：

90、wel(x)＝pf(x)·el(x)??(21)

91、其中，

92、步驟52：基于多起始點bfgs(multiple?starting?point?broyden-fletcher-goldfarb-shanno，msp-bfgs)[16]全局優化算法對wei函數進行優化，得到下一個最優設計點

93、步驟53：從和最優成品率候選集b中選擇一個具有最高熵搜索函數es值的設計點

94、給定觀測數據x*代表未知的全局最優成品率設計點。es函數從信息論的角度出發，試圖找到最大化x*信息增益的設計點，定義為[17]

95、

96、h(px*)＝-px*·log(px*)??(23)

97、其中h()為交叉熵，d′o＝do∪(x，y(x))，其中y(x)為設計點x的預測漸進成品率。和分別表示在觀測數據集do和do′下，設計空間中設計點成為全局最優成品率設計點x*的概率分布。

98、由于和沒有解析形式，本發明使用mc方法來近似估計es函數值。首先利用馬爾科夫蒙特卡洛(markov?chain?monte?carlo，mcmc)采樣法，以wei函數為目標分布進行采樣，從中挑選100個具有最大wei值的設計點。在當前數據集do下，預測漸進成品率服從公式(18)和(19)定義的后驗分布，針對每個設計點按照公式(18)和(19)定義的后驗分布進行一次隨機采樣，得到向量重復500次隨機采樣，即可得到矩陣表示第j列中最大的元素，p*表示100個設計點成為最優成品率設計點的概率向量，其元素p*i為

99、

100、其中，當時，否則為0。p*即為的mc近似。

101、將和最優成品率候選集b中的設計點，分別加入do得到do′。重復上述步騾，即可得到的mc近似。

102、利用公式(22)，計算和最優成品率候選集b中設計點的熵搜索函數es值，選擇具有最高es值的設計點作為

103、步驟5.4：針對分配nbatch個仿真點進行成品率分析。

104、本發明中，如果即新設計點是最有希望成為最優設計的點，則最優成品率候選集b中設計點的成品率分析過程將被暫時凍結，并在新設計點上執行一批nbatch個仿真點的粗糙成品率分析。否則，為最優成品率候選集b中某個候選設計點，則對該點執行一批nbatch個仿真點的成品率分析，進一步提升該點成品率分析的準確度。

105、步驟55：將步驟54新得到的數據點加入數據集中，并根據公式(8)在當前數據集上重新構造最優成品率候選集b。若成品率未滿足要求并且迭代次數k小于最大迭代次數nmax，則跳轉至步驟4，進行迭代優化；否則優化結束，輸出最優設計參數和相應的成品率結果。

106、本發明提供了利用凍融高斯過程回歸模型對模擬電路成品率建模，預測漸進成品率的方法。本方法還包括通過求解一個tt工藝角模擬電路性能優化問題，搜索剛好滿足性能約束的設計點，并將這些點作為凍融貝葉斯優化熱啟動的初始點，可進一步提高成品率優化的收斂速度。經實驗結果表明，本方法明顯優于現有技術方法，能大幅減少模擬電路成品率優化所需仿真次數。

107、本發明的優點在于：

108、1)提出將凍融貝葉斯優化技術應用于模擬電路的成品率優化，自動引導設計空間的搜索，逐步提高工藝空間的成品率分析準確度，充分利用了貝葉斯優化的高采樣效率和凍融技術的靈活性，提升模擬電路成品率優化效率；2)通過在成品率優化框架中求解一個tt工藝角下標稱性能優化問題，有效挖掘電路性能中隱藏的先驗信息，進一步降低成品率優化的仿真成本；3)實驗結果表明，本發明與現有技術的模擬電路成品率優化方法相比，在不降低優化精度的條件下，仿真時間加速比為2.47～573倍。