一種用料最省的同型容器陣的制作方法

本實用新型涉及建造技術領域，尤其涉及一種用料最省的同型容器陣。

背景技術：

在海產品養殖領域中，漁民需要建造多個相互隔離的養殖池，一方面將自己家的養殖池與別人家的隔離開來，另外也將不同種類的海產品分隔開來。當單個養殖池的容積一定時，需要考慮如何設計池子的形狀或結構，以達到用料最省的目的。

在化工行業中，化工企業往往需要根據不同的產品、訂單、工期等因素，在廠區建造許多化學反應池。對于同一規格型號的反應池，同樣需要考慮設計池子的形狀及結構，使用料最省，從而節省成本。

分析上述養殖池和化學反應池的問題背景可知：

(1)無論是養殖池，還是化學反應池，其形狀構造都可以用幾何體進行描述；

(2)建造池子所用材料的厚度相對于池子面積的量級，可以忽略，因此用料多少僅與池子的面積有關。

(3)建造池子時，不需要真正的建造上表面，只需要建造側面和底面，所以所述的“用料最省”就是指池子的側面與底面面積之和最小。

(4)一般建造養殖池和化學反應池時，其厚度是均勻的。且池壁的拐角處，用料厚度的重疊造成的數量損失為0，這是因為材料的厚度相對于池子的體積和面積來說是一個很小的量，可以不考慮用料厚度的重疊造成的數量損失。

技術實現要素：

有鑒于此，本實用新型提供了一種用料最省的同型容器陣，在單個容器的體積一定的條件下，通過容器形狀結構的設計，使其表面積最小。且所有容器的上表面開口處于同一個平面中，以充分利用空間。

為了解決上述技術問題，本實用新型是這樣實現的：

一種用料最省的同型容器陣，包括：該容器陣由多個上表面開口的單個容器組成；單個容器的幾何體形狀為一個尖底的正六棱柱；每個單個容器的上端面為一個正六邊形，正六邊形的邊長為V為容器幾何體的體積；容器的6個棱邊包括3個長棱和3個短棱，長棱和短棱兩兩相間；長棱的長度為短棱的長度為6個棱邊采用三個向內傾斜的菱形相連，三個菱形最后匯聚在一點，該點即為正六棱柱尖底的尖部。

其中，所有容器的上端面處于同一水平面，且以正六邊形的邊作為連接。

其中，所述容器為養殖池或化學反應池或化學試管。

有益效果：

利用本實用新型提出的方案所建造的同型容器陣，能在保證體積一定的情況下所用的材料最少。

而且，由于所建的容器上端面是正六邊形，在所有容器都緊挨著的情況下，可以保證所有容器上端面所構成的平面沒有任何空余地方，能最大限度的利用空間。

附圖說明

圖1為正六邊形填滿一個平面的示意圖；

圖2為正六棱柱體的結構示意圖；

圖3為倒立后的正六棱柱體的結構示意圖；

圖4為尖頂正六棱柱體的構造過程示意圖；

圖5為尖頂正六棱柱體的結構示意圖；

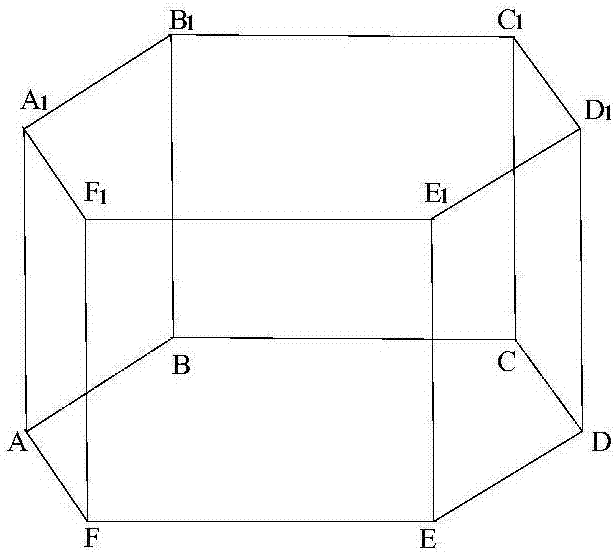
圖6為本實用新型提出的尖底正六棱柱池子的結構示意圖。

具體實施方式

下面結合附圖并舉實施例，對本實用新型進行詳細描述。

本實用新型提供了一種用料最省的同型容器陣，其基本思想是：該容器陣由多個上表面開口的單個容器組成；單個容器的幾何體形狀為一個尖底的正六棱柱；每個單個容器的上端面為一個正六邊形，容器的6個棱邊包括3個長棱h和3個短棱Ld，長棱和短棱兩兩相間；6個棱邊采用三個向內傾斜的菱形相連，三個菱形最后匯聚在一點，該點即為正六棱柱尖底的尖部。

下面對本實用新型的原理進行詳細描述。

1、確定池子投影的輪廓

對于“幾何體的體積一定，表面積最小”的問題，可將幾何體投影到二維平面中，就變成是“面積一定，周長最小”問題。根據幾何知識可知，對于多邊形，包圍同樣的面積，正多邊形的周長最短。所以，設計的池子上端面應該是正多邊形。

2、確定正多邊形的邊數

分析正多邊形的特點可知，能夠填滿一個二維無限平面的正多邊形只有三角形、正方形和正六邊形。證明過程如下：

因為正n邊形的每個內角值為：

如果正n邊形能夠填滿一個無限平面，在交點處會有整數Z個正n邊形的頂點交于一點，則有：

對于上式，只有n＝3或4、或6時，Z為合理的正整數。也就是說，正多邊形的邊數只能為正三角形、正四邊形或正六角形，這三種情況中的一種。

假設上述正多邊形的面積為S，對于正三角形，設其邊長為L3，則有：

根據上式可以解得：

此時，正三角形的周長C3為：

對于正四邊形，設其邊長為L4，則有：

S＝L₄×L₄

根據上式可以解得：

此時，正四邊形的周長C4為：

對于正六邊形，設其邊長為L6，則有：

根據上式可以解得：

此時，正六邊形的周長C6為：

可見，在面積一定的情況下，正六邊形的周長最小。

所以池子在高度方向上的輪廓形狀就確定為正六棱柱體。如附圖1所示，為一組正六邊形組成的平面。

3、確定正六棱柱體的邊長和高度

在正六棱柱體的體積一定的條件下，需要確定其底面的邊長和高度，使其表面積最小。

設正六棱柱體的體積為V，邊長為a，高度為h。那么，正六棱柱體的底面積S_d為：

正六棱柱體的體積V可以表示為：

則正六棱柱體的高h可以表示為：

設正六棱柱體的表面積為S_b，其包括1個底面面積S_d和6個側面面積S_c，可以表示為：

要使得正六棱柱體在體積一定的條件下，表面積最小，就需要選取合適的a值，使得S_b達到最小值。通過對S_b求導，得出：

令S_b’＝0，得出：

此時，

特別的，可以得出：

因此，可以得出如下結論：如果單個正六棱柱的體積為常數V，那么正六棱柱表面積最小時，邊長為高為正六棱柱的高與邊長之比為如附圖2所示，為一個正六棱柱結構體。

4、正六棱柱體底面修正

附圖2所示的正六棱柱體，上端面A₁B₁C₁D₁E₁F₁是空的，不需要用料建設，而下底面ABCDEF是實的，需要用料建設。為了論述的方便，將附圖2所示的正六棱柱上下翻轉180度來進行分析，如附圖3所示。

對于附圖3所示的結構，沿著對角線AC，斜向做切面ACP₁，將頂點B所在部分切下，得到一個三棱錐BACP₁，然后以直線AC為轉軸，將三棱錐BACP₁向上旋轉180度，其過程如附圖4所示。旋轉后得到的結構如附圖5所示，三棱錐的頂點B會旋轉至正六邊形的中心點O處；三棱錐BACP₁旋轉前的面ABC，旋轉后與三角形ACO重合；P點處于正六邊形ABCDEF中心點O正上方，且線段PO與線段BP₁長度相等，三棱錐BACP₁的P₁點旋轉后與P點重合。所以三棱錐旋轉后的面ACP₁就是附圖5中所示的面ACP；根據對稱的特性可知，三棱錐BACP₁旋轉前的面ACP₁與三棱錐旋轉后得到的面ACP共面。

同樣的，如附圖4所示，分別沿著對角線EC和AE，重復上述操作過程。就會得到如附圖5所示的尖頂正六棱柱體。顯然四邊形APCP₁、APEP₃、CPEP₂是全等的菱形。

對于附圖5中的尖頂正六棱柱體，其表面積由6個全等側面CP₁B₁C₁等和3個全等菱形頂面APCP₁構成。即：

S＝6·S(CP₁B₁C₁)+3·S(APCP1)

在附圖4中，四邊形CP₁B₁C₁的面積可用矩形BCC₁B₁減去三角形BCP₁得到，令∠BCP₁＝θ，有：

附圖5中，菱形APCP₁的邊長其中的一條對角線在等腰三角形AP₁C里面，有：

所以：

所以菱形APCP₁的面積為：

綜合以上分析得出，尖頂正六棱柱體的表面積為：

令x＝tanθ

記：

由于附圖4中所示的正六棱柱ABCDEF-A₁B₁C₁D₁E₁F₁的邊長a和高h在前面的論述中已經確定。于是，在這里求尖頂正六棱柱體表面積S的最小值問題，就等價于求f(x)的最小值問題，對f(x)求導，得到：

令f′(x)＝0，得到：

故:

即

所以，當時，尖頂正六棱柱表面積S取最小值。

5、結構參數計算

令附圖5中斜向菱形APCP₁的內角∠PCP1＝α，根據以上分析過程，可知：

故：

利用幾何關系，可推導出：

α＝∠PCP1＝70.5°

令尖頂正六棱柱的短棱B₁P₁的長度為Ld，可得：

Ld＝B₁P₁＝BB₁-BC·tanθ＝h-a·tanθ

將步驟(3)中計算得到的邊長a和長棱h的值，以及步驟(4)中計算得到的的結論代入上式，可得：

令尖頂正六棱柱體的頂點P到正六邊形ABCDEF的垂直高度為Hp，則有：

6、翻轉

將附圖5所示的尖頂正六棱柱體再上下翻轉180度，成為尖底正六棱柱體，如附圖6所示，則為本實用新型所要建造的池子的結構。

即本實用新型的解決方案是：

本實用新型的解決方案是：

所述單個池子，其上端面為一個正六邊形，整個池子的幾何體的形狀為一個尖底的正六棱柱，即該池子從上方投影在二維平面后，是一個正六邊形。根據需要，依次布置構建多個池子，所有池子的上端面處于同一水平面，且將整個平面布滿，所有池子所構成的上平面之間沒有多余的空隙。

設單個幾何體的體積為V，則每個幾何體的構造過程為：

(1)先根畫出一個正六邊形區域，該正六邊形區域做為池子的上表面正六邊形的邊長a為

(2)以上述正六邊形各邊的交點為基礎，向下建造長棱h和短棱Ld。其中長、短棱兩兩相間，長棱長度為短棱長度為

(3)以長棱和短棱下方的端點為基礎，建造3個斜向菱形，斜向菱形平面由對應的一個短棱端點和兩個長棱端點確定(三點確定一個平面)，并且把這3個點作為菱形的3個相鄰頂點，建造時保持菱形的內角為70.5°，三個菱形的第四個點共點，距離上表面投影在正六邊形的中心。

(4)根據需要，依次構建多個完全相同的池子。任意兩個相鄰的池子，其上端面共用一個邊，并相應的共用有該邊向下延伸的側壁。

綜上所述，以上僅為本實用新型的較佳實施例而已，并非用于限定本實用新型的保護范圍。凡在本實用新型的精神和原則之內，所作的任何修改、等同替換、改進等，均應包含在本實用新型的保護范圍之內。