鐵路鋼箱梁橋溫度梯度模式評價方法與流程

本發明屬于橋梁溫度檢測技術領域，具體涉及到一種鐵路鋼箱梁橋溫度梯度模式的評價方法。

背景技術：

鋼箱梁橋是長期暴露在自然環境中的結構物，在長期的使用過程中必然受到太陽輻射及其周圍環境氣溫等的影響，這些都會影響到橋梁結構的溫度分布，產生溫度梯度，從而產生溫度變形，當鋼箱梁橋內外約束阻礙結構的變形時就會產生相當大的溫度應力，因此在橋梁結構中的溫度效應不容忽視；而研究鋼橋結構的溫度效應前，首先應對鋼橋結構的溫度梯度進行研究，給出適合于我國的溫度梯度模式。

鋼箱梁橋溫度荷載形成的根本原因在于太陽能量的傳輸和地球自身的運動，以及當地氣象環境、地理條件。橋梁結構上的溫度作用分為均勻溫度作用和梯度溫度作用。梯度溫度作用又可分為豎向溫度梯度作用和橫向溫度梯度作用。溫度梯度作用在橋梁結構上會引起溫度自約束應力，即結構內部纖維間溫度不同，產生的應變差受到纖維間相互約束而引起應力。橋梁結構在日照作用下產生顯著溫度效應的現象最早于20世紀50年代由前聯邦德國學者發現。近幾十年來，國內外都發生了由溫度應力導致橋梁結構發生嚴重損壞的事故。

國內外學者對橋梁結構溫度作用的早期研究均集中于混凝土橋梁，提出了一系列研究方法并取得了一些研究成果。但隨著橋梁結構設計理論的日益成熟與施工技術的發展，大跨度鐵路鋼箱梁橋的使用日益增加，亟需對鐵路鋼箱梁橋的溫度分布進行規定，以保證鐵路鋼箱梁橋施工和使用過程中的安全。而我國鐵路橋涵設計規范對于鐵路鋼箱梁橋設計溫差標準值尚無明確規定，原因在于得到具有一定重現期的截面溫差標準值需要建立在長期廣泛的現場實測的基礎上，所獲得的實測數據數量龐大且后期數據處理工作量巨大。

我國現行的《鐵路橋梁鋼結構設計規范》對鋼梁溫度梯度取值沒有進行規定。同時，我國現行的《公路橋涵設計通用規范》(jtgd60—2004)規定的溫度梯度模式參照美國aashto規范而得，且只給出了鋪裝后混凝土梁與鋼-混組合梁的日照溫度梯度。工程設計一般參照英國橋梁規范bs-5400對結構溫度效應進行估算，然而，由于各國的日照、氣象、地理環境等影響橋梁結構溫度分布的外在環境因素的不同，bs-5400溫度梯度曲線不一定適用于中國的橋梁結構。因此，在對某鐵路鋼箱梁進行長期的溫度監測之后，對溫度數據進行有效的整理分析以得到適用于鐵路鋼箱梁橋溫度梯度模式是非常必要的。

技術實現要素：

本發明所要解決的技術問題在于提供一種鐵路鋼箱梁橋溫度梯度模式評價方法，目的在于得到適用于我國鐵路鋼箱梁橋的溫度梯度模式。

本發明的技術方案是由以下步驟實現的：

(1)在鋼箱梁橋腹板和頂板上布置溫度測點并采集溫度，每次采集時間間隔為2～5分鐘；

(2)將采集獲得的鋼箱梁橋溫度進行分析，找出腹板各測點的日極值溫差值所對應時刻的溫度數據，以溫度為橫坐標，腹板測點間的距離為縱坐標，作出梯度散點圖，并采用最小二乘法進行曲線擬合，得到豎向溫度梯度曲線；找出頂板各測點的日極值溫差值所對應時刻的溫度數據，以溫度為橫坐標，頂板測點間的距離為縱坐標，作出梯度散點圖，并采用最小二乘法進行曲線擬合，得到橫向溫度梯度曲線；

(3)將得到的溫度梯度曲線簡化成折線，為溫度梯度模式；

(4)得到豎向溫度梯度模式腹板各折點的日極值溫差值和橫向溫度梯度模式頂板各折點的日極值溫差值；

腹板各折點日極值溫差值為各折點處測點溫度值減去腹板測點最低溫度值，頂板各折點的日極值溫差值為頂板各折點處測點溫度值減去頂板測點最低溫度值；

(5)對鋼箱梁橋的頂板和腹板各個折點的日極值溫差值進行統計分析，得到溫差概率分布直方圖，再對直方圖進行概率擬合，得到日極值溫差概率密度函數；

統計頂板和腹板各個折點的日極值溫差值并輸入到計算機，應用origin8.0數理統計分析軟件分別做出頂板和腹板的各折點的日極值溫差值的概率直方圖，再分別對頂板和腹板各折點的日極值溫差值的概率直方圖進行函數擬合，得到對應的概率密度函數f(x)；

(6)通過概率密度函數p0，計算設計基準期為100年，不同重現期n的溫差標準值t；

概率密度函數f(x)所對應的分布函數為fx(x)，則設計基準期100年內的頂板和各個折點的極值溫差值的累積分布函數fy(x)為：fy(x)＝[fx(x)]¹⁰⁰；

溫差標準值的保證率為p0，對鐵路鋼箱梁橋施工期溫度設計標準值進行取值，可將兩年作為施工期設計基準期，分別取半年、一年作為施工期溫度作用重現期，則施工期內極值溫差作用的溫差標準值的保證率分別為96％、98％；式中fy(x)為p0，計算得x為溫差標準值t；

(7)為方便在實際工程中的應用，對不同重現期無鋪裝和鋪裝后鐵路鋼箱梁的溫差標準值進行偏安全取整，得到溫差標準值的建議值。

上述的步驟(1)在腹板和頂板上布置溫度測點為：兩側腹板布置溫度測點位置以距頂板的垂直距離表示為0.0m，0.05m，0.1m，0.2m，0.3m，0.6m，1.2m，2.4m，4.15m和腹板與底板相交處；頂板溫度測點布置位置，以距離右側腹板的水平距離表示為：0.0m，1.4m，2.8m，4.2m。

上述的鋼箱梁橋為無鋪裝鋼箱梁橋，無鋪裝鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值正溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝18.7，σ＝3.50，重現期n＝50年，t1＝31.1℃；重現期n＝100年，t1＝31.7℃；施工階段重現期n＝0.5年，t1＝15.4℃；施工階段重現期n＝1.0年，t1＝16.2℃；

無鋪裝鋼箱梁橋豎向溫度梯度模式中距腹板頂部0.2m處折點日極值正溫差標準值t2符合正態分布，其概率密度函數為：

式中μ＝9.40，σ＝2.91，重現期n＝50年，t2＝19.6℃；重現期n＝100年，t2＝20.2℃；施工階段重現期n＝0.5年，t2＝15.4℃；施工階段重現期n＝1.0年，t2＝16.2℃；

無鋪裝鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值負溫差標準值t1符合極值ⅰ型分布，其概率密度函數為：

式中μ＝-2.70，σ＝0.68，重現期n＝50年，t1＝-8.5℃；重現期n＝100年，t1＝-9.0℃；施工階段重現期n＝0.5年，t1＝-5.4℃；施工階段重現期n＝1.0年，t1＝-5.8℃；

無鋪裝鋼箱梁橋橫向溫度梯度模式中距兩側腹板1.4m處日極值正溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝6.79，σ＝1.18，重現期n＝50年，t1＝11.0℃；重現期n＝100年，t1＝11.2℃；施工階段重現期n＝0.5年，t1＝9.2℃；施工階段重現期n＝1.0年，t1＝9.5℃；

無鋪裝鋼箱梁橋橫向溫度梯度模式中距兩側腹板1.4m處日極值負溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝-2.32，σ＝1.01，重現期n＝50年，t1＝-5.9℃；重現期n＝100年，t1＝-6.1℃；施工階段重現期n＝0.5年，t1＝-4.4℃；施工階段重現期n＝1.0年，t1＝-4.7℃；

上述的鋼箱梁橋為混凝土鋪裝層鋼箱梁橋，混凝土鋪裝層鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值正溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝5.13，σ＝3.50，重現期n＝50年，t1＝15.8℃；重現期n＝100年，t1＝16.0℃；施工階段重現期n＝0.5年，t1＝12.3℃；施工階段重現期n＝1.0年，t1＝13.3℃；

混凝土鋪裝層鋼箱梁橋豎向溫度梯度模式中距腹板頂部0.2m處折點日極值正溫差標準值t2符合正態分布，其概率密度函數為：

式中μ＝3.30，σ＝1.00，重現期n＝50年，t2＝6.8℃；重現期n＝100年，t2＝7.0℃；施工階段重現期n＝0.5年，t2＝5.4℃；施工階段重現期n＝1.0年，t2＝5.6℃；

混凝土鋪裝層鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值負溫差標準值t1符合極值ⅰ型分布，其概率密度函數為：

式中μ＝-1.26，σ＝0.62，重現期n＝50年，t1＝-6.5℃；重現期n＝100年，t1＝-7.0℃；施工階段重現期n＝0.5年，t1＝-3.7℃；施工階段重現期n＝1.0年，t1＝-4.1℃；

混凝土鋪裝層鋼箱梁橋橫向溫度梯度模式中距兩側腹板1.4m處日極值正溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝2.56，σ＝0.88，重現期n＝50年，t1＝5.7℃；重現期n＝100年，t1＝5.8℃；施工階段重現期n＝0.5年，t1＝4.4℃；施工階段重現期n＝1.0年，t1＝4.6℃；

混凝土鋪裝層鋼箱梁橋橫向溫度梯度模式中腹板頂部日極值負溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝-1.46，σ＝0.85，重現期n＝50年，t1＝-4.5℃；重現期n＝100年，t1＝-4.6℃；施工階段重現期n＝0.5年，t1＝-3.2℃；施工階段重現期n＝1.0年，t1＝-3.5℃；

5、根據權利要求1或2所述的鐵路鋼箱梁橋溫度梯度模式評價方法，其特征在于：所述的鋼箱梁橋為道砟鋪裝層鋼箱梁橋，道砟鋪裝層鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值正溫差標準值t1符合極值ⅰ型分布，其概率密度函數為：

式中μ＝2.58，σ＝1.17，重現期n＝50年，t1＝12.5℃；重現期n＝100年，t1＝13.4℃；施工階段重現期n＝0.5年，t1＝7.1℃；施工階段重現期n＝1.0年，t1＝8.0℃；

道砟鋪裝層鋼箱梁橋豎向溫度梯度模式中距腹板頂部0.05m處折點日極值正溫差標準值t2符合正態分布，其概率密度函數為：

式中μ＝2.20，σ＝1.35，重現期n＝50年，t2＝6.9℃；重現期n＝100年，t2＝7.2℃；施工階段重現期n＝0.5年，t2＝5.0℃；施工階段重現期n＝1.0年，t2＝5.3℃；

道砟鋪裝層鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值負溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝-2.52，σ＝2.24，重現期n＝50年，t1＝-9.0℃；重現期n＝100年，t1＝-9.2℃；施工階段重現期n＝0.5年，t1＝-7.1℃；施工階段重現期n＝1.0年，t1＝-7.7℃；

道砟鋪裝層鋼箱梁橋橫向溫度梯度模式中在距兩側腹板1.4m處日極值正溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝1.00，σ＝0.70，重現期n＝50年，t1＝3.5℃；重現期n＝100年，t1＝3.6℃；施工階段重現期n＝0.5年，t1＝2.5℃；施工階段重現期n＝1.0年，t1＝2.6℃；

道砟鋪裝層鋼箱梁橋橫向溫度梯度模式中距兩側腹板1.4m處日極值負溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝-1.87，σ＝0.94，重現期n＝50年，t1＝-5.2℃；重現期n＝100年，t1＝-5.4℃；施工階段重現期n＝0.5年，t1＝-3.8℃；施工階段重現期n＝1.0年，t1＝-4.1℃；

道砟鋪裝層鋼箱梁橋橫向溫度梯度模式中腹板頂部日極值負溫差標準值t2符合正態分布，其概率密度函數為：

式中μ＝-0.60，σ＝0.33，重現期n＝50年，t1＝-1.7℃；重現期n＝100年，t1＝-1.8℃；施工階段重現期n＝0.5年，t1＝-1.3℃；施工階段重現期n＝1.0年，t1＝-1.4℃。

本發明基于對某鐵路鋼箱梁現場溫度監測數據的分析，提出無鋪裝、混凝土鋪裝和道砟鋪裝鋼箱梁橫向和豎向溫度梯度模式，并通過對現場溫度監測數據的日極值溫差進行數理統計分析，得到不同鋪裝鐵路鋼箱梁在不同重現期下橫向和豎向的溫差標準值，可用于計算鐵路鋼箱梁不同施工階段溫度梯度產生的附加應力和變形，保障安全施工和正常運營，為完善我國相關設計規范提供依據。

附圖說明

圖1是無鋪裝鋼箱梁橋腹板豎向正溫度梯度曲線圖。

圖2是無鋪裝鋼箱梁橋腹板豎向負溫度梯度曲線圖。

圖3是無鋪裝鋼箱梁橋腹板豎向正溫度梯度圖。

圖4是無鋪裝鋼箱梁橋腹板豎向負溫度梯度圖。

圖5是無鋪裝鋼箱梁橋腹板橫向正溫度梯度曲線圖。

圖6是無鋪裝鋼箱梁橋腹板橫向負溫度梯度曲線圖。

圖7是混凝土鋪裝鋼箱梁橋腹板豎向正溫度梯度曲線圖。

圖8是混凝土鋪裝鋼箱梁橋腹板豎向負溫度梯度曲線圖。

圖9是混凝土鋪裝鋼箱梁橋腹板豎向正溫度梯度圖。

圖10是混凝土鋪裝鋼箱梁橋腹板豎向負溫度梯度圖。

圖11是混凝土鋪裝鋼箱梁橋腹板橫向正溫度梯度曲線圖。

圖12是混凝土鋪裝鋼箱梁橋腹板橫向負溫度梯度曲線圖。

圖13是道砟層鋪裝鋼箱梁橋腹板豎向正溫度梯度曲線圖。

圖14是道砟層鋪裝鋼箱梁橋腹板豎向負溫度梯度曲線圖。

圖15是道砟層鋪裝鋼箱梁橋腹板豎向正溫度梯度圖。

圖16是道砟層鋪裝鋼箱梁橋腹板豎向負溫度梯度圖。

圖17是道砟層鋪裝鋼箱梁橋腹板橫向正溫度梯度曲線圖。

圖18是道砟層鋪裝鋼箱梁橋腹板橫向負溫度梯度曲線圖。

圖19是無鋪裝鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值正溫差標準值t1的概率直方圖。

圖20是無鋪裝鋼箱梁橋豎向溫度梯度模式中距腹板頂部0.2m處折點日極值正溫差標準值t2的概率直方圖。

圖21是無鋪裝鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值負溫差標準值t1的概率直方圖。

圖22是無鋪裝鋼箱梁橋橫向溫度梯度模式中距兩側腹板1.4m處日極值正溫差標準值t1的概率直方圖。

圖23是無鋪裝鋼箱梁橋橫向溫度梯度模式中距兩側腹板1.4m處日極值負溫差標準值t1的概率直方圖。

圖24是混凝土鋪裝鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值正溫差標準值t1的概率直方圖。

圖25是混凝土鋪裝鋼箱梁橋豎向溫度梯度模式中距腹板頂部0.2m處折點日極值正溫差標準值t2的概率直方圖。

圖26是混凝土鋪裝鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值負溫差標準值t1的概率直方圖。

圖27是混凝土鋪裝鋼箱梁橋橫向溫度梯度模式中距兩側腹板1.4m處日極值正溫差標準值t1的概率直方圖。

圖28是混凝土鋪裝鋼箱梁橋橫向溫度梯度模式中腹板頂部日極值負溫差標準值t1的概率直方圖。

圖29是道砟層鋪裝鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值正溫差標準值t1的概率直方圖。

圖30是道砟層鋪裝鋼箱梁橋豎向溫度梯度模式中距腹板頂部0.05m處折點日極值正溫差標準值t2的概率直方圖。

圖31是道砟層鋪裝鋼箱梁橋豎向溫度梯度模式中腹板頂部日極值負溫差標準值t1的概率直方圖。

圖32是道砟層鋪裝鋼箱梁橋橫向溫度梯度模式中距兩側腹板1.4m處日極值正溫差標準值t1的概率直方圖。

圖33是道砟層鋪裝鋼箱梁橋橫向溫度梯度模式中距兩側腹板1.4m處日極值負溫差標準值t1的概率直方圖。

圖34是道砟層鋪裝鋼箱梁橋橫向溫度梯度模式中腹板頂部日極值負溫差標準值t2的概率直方圖。

具體實施方式

下面結合附圖和實施例對本發明進一步詳細說明，但本發明不限于下述的實施方式。

實施例1

1、在無鋪裝鋼箱梁橋腹板和頂板上布置溫度測點并采集溫度，每次采集時間間隔為3分鐘，每次采集時間間隔也可為2分鐘，每次采集時間間隔還可為5分鐘；

參照英國規范bs-5400對鋼橋溫度梯度的規定，在無鋪裝層鋼箱梁兩側腹板布置溫度測點，溫度測點位置以距頂板的垂直距離表示為0.0m，0.05m，0.1m，0.2m，0.3m，0.6m，1.2m，2.4m，4.15m和腹板與底板相交處；在頂板布置溫度測點，溫度測點位置以距離右側腹板的水平距離表示為：0.0m，1.4m，2.8m，4.2m；每隔3分鐘采集一次各測點溫度并記錄。

2、將采集獲得的無鋪裝層鋼箱梁橋溫度進行分析，找出腹板各測點日極值溫差值所對應時刻的溫度數據，以溫度為橫坐標，測點間的距離為縱坐標，作出梯度散點圖，并采用最小二乘法進行曲線擬合，得到豎向溫度梯度曲線；找出混凝土頂板各測點的日極值溫差值所對應時刻的溫度數據，以溫度為橫坐標，混凝土頂板測點間的距離為縱坐標，作出梯度散點圖，并采用最小二乘法進行曲線擬合，得到橫向溫度梯度曲線；

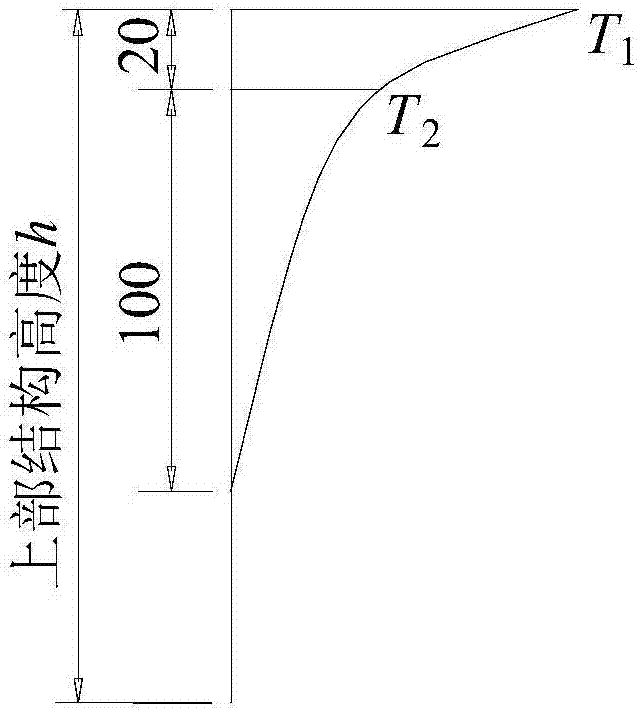
在距腹板頂部1.2m內采用非線性擬合，在距頂板1.2m到腹板底部范圍內采用線性擬合，得到豎向正溫度梯度曲線，如圖1所示；在距腹板頂部1.2m范圍內采用非線性擬合，在距腹板頂部1.2m至腹板底部范圍內采用線性擬合，得到豎向負溫度梯度曲線，如圖2所示；頂板上距右側腹板1.4m至2.8m處的溫度較高采用線性擬合，距右側腹板0.0m處測點和4.2m處測點的溫度較低且相近，得到呈梯形的橫向正溫度梯度曲線如圖5所示；頂板上距右側腹板1.4m至2.8m處的溫度較低采用線性擬合，距右側腹板0.0m處測點和4.2m處測點的溫度較高且相近，得到呈倒梯形的橫向負溫度梯度曲線如圖6所示。

3、將得到的溫度梯度曲線簡化成折線，為溫度梯度模式；

對豎向正溫度梯度曲線簡化，在距腹板頂部0.2m內采用直線簡化，在距腹板頂部0.2m到1.2m范圍內采用直線簡化，0.2m處為折點，得到豎向正溫度梯度模式如圖3所示；

對豎向負梯度曲線簡化，在距腹板頂部1.2m內采用直線簡化，1.2m處為折點，得到豎向負溫度梯度模式如圖4所示；

橫向正負溫度梯度曲線均為折線形，不需要簡化。

4、得到豎向溫度梯度模式腹板各折點的日極值溫差值和橫向溫度梯度模式頂板各折點的日極值溫差值；

腹板各折點日極值溫差值為各折點處測點溫度值減去腹板測點最低溫度值，頂板各折點的日極值溫差值為頂板各折點處測點溫度值減去頂板測點最低溫度值；

5、對鋼箱梁橋的頂板和腹板各個折點的日極值溫差值進行統計分析，得到溫差概率分布直方圖，再對直方圖進行概率擬合，得到日極值溫差概率密度函數；

統計頂板和腹板各個折點的日極值溫差值并輸入到計算機，應用origin8.0數理統計分析軟件分別做出頂板和腹板各個折點的日極值溫差值的概率直方圖，再分別對頂板和腹板各個折點的日極值溫差值的概率直方圖進行函數擬合，得到對應的概率密度函數f(x)：

豎向溫度梯度模式中腹板頂部日極值正溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝18.7，σ＝3.50，如圖19所示；

豎向溫度梯度模式中距腹板頂部0.2m處折點日極值正溫差標準值t2符合正態分布，其概率密度函數為：

式中μ＝9.40，σ＝2.91，如圖20所示；

豎向溫度梯度模式中腹板頂部日極值負溫差標準值t1符合極值ⅰ型分布，其概率密度函數為：

式中μ＝-2.70，σ＝0.68，如圖21所示；

橫向溫度梯度模式中距兩側腹板1.4m處日極值正溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝6.79，σ＝1.18，如圖22所示；

無鋪裝鋼箱梁橋橫向溫度梯度模式中距兩側腹板1.4m處日極值負溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝-2.32，σ＝1.01，如圖23所示；

6、通過概率密度函數f(x)，計算設計基準期為100年，不同重現期n的溫差標準值t。

概率密度函數f(x)所對應的分布函數為fx(x)，則設計基準期100年內的頂板和各個折點的極值溫差值的累積分布函數fy(x)為：fy(x)＝[fx(x)]¹⁰⁰；

溫差標準值的保證率為p0，對鐵路鋼箱梁橋施工期溫度設計標準值進行取值，可將兩年作為施工期設計基準期，分別取半年、一年作為施工期溫度作用重現期，則施工期內極值溫差作用的溫差標準值的保證率分別為96％、98％；令fy(x)＝p0，計算得x為溫差標準值t。

無鋪裝鋼箱梁豎向溫差標準值見表1，橫向溫差標準值見表2。

7、為方便在實際工程中的應用，對不同重現期無鋪裝鐵路鋼箱梁的溫差標準值進行偏安全取整，得到溫差標準值的建議值。

無鋪裝鐵路鋼箱梁豎向溫差標準值的建議值見表3，橫向溫差標準值的建議值見表4。

實施例2

1、在混凝土鋪裝鋼箱梁橋腹板和頂板上布置溫度測點并采集溫度，每次采集時間間隔為3分鐘；每次采集時間間隔也可為2分鐘，每次采集時間間隔還可為5分鐘；

參照英國規范bs-5400對鋼橋溫度梯度的規定，在混凝土鋪裝層鋼箱梁兩側腹板布置溫度測點，溫度測點位置以距頂板的垂直距離表示為0.0m，0.05m，0.1m，0.2m，0.3m，0.6m，1.2m，2.4m，4.15m和腹板底部；在頂板布置溫度測點，溫度測點位置以距離右側腹板的水平距離表示為：0.0m，1.4m，2.8m，4.2m；每隔3分鐘采集一次各測點溫度并記錄。

2、將采集獲得的混凝土鋪裝層鋼箱梁橋溫度進行分析，找出腹板各測點日極值溫差值所對應時刻的溫度數據，以溫度為橫坐標，測點間的距離為縱坐標，作出梯度散點圖，并采用最小二乘法進行曲線擬合。

在距腹板頂部1.2m內采用非線性擬合，在距頂板1.2m到腹板底部范圍內采用線性擬合，得到豎向正溫度梯度曲線，如圖7所示；在距腹板頂部2.4m范圍內采用非線性擬合，得到豎向負溫度梯度曲線，如圖8所示；頂板上距右側腹板1.4m至2.8m處的溫度較高采用線性擬合，距右側腹板0.0m處測點和4.2m處測點的溫度較低且相近，得到呈梯形的橫向正溫度梯度曲線如圖11所示；頂板與陰面腹板的交點處溫度最低，頂板與陽面腹板交點處溫度最高，得到呈線性分布的橫向負溫度梯度曲線如圖12所示。

3、將得到的溫度梯度曲線簡化成折線，為溫度梯度模式；

對豎向正溫度梯度曲線簡化，在距腹板頂部0.2m內采用直線簡化，在距腹板頂部0.2m到2.4m范圍內采用直線簡化，0.2m處為折點，得到豎向正溫度梯度模式如圖9所示；

對豎向負梯度曲線簡化，在距腹板頂部2.4m內采用直線簡化，得到豎向負溫度梯度模式如圖10所示；

橫向正負溫度梯度曲線均為折線形，不需要簡化。

4、得到豎向溫度梯度模式腹板各折點的日極值溫差值和橫向溫度梯度模式頂板各折點的日極值溫差值；

腹板各折點日極值溫差值為各折點處測點溫度值減去腹板測點最低溫度值，頂板各折點的日極值溫差值為頂板各折點處測點溫度值減去頂板測點最低溫度值；

5、對鋼箱梁橋的頂板和腹板各個折點的日極值溫差值進行統計分析，得到溫差概率分布直方圖，再對直方圖進行概率擬合，得到日極值溫差概率密度函數；

統計頂板和腹板各個折點的日極值溫差值并輸入到計算機，應用origin8.0數理統計分析軟件分別做出頂板和腹板各個折點的日極值溫差值的概率直方圖，再分別對頂板和腹板各個折點的日極值溫差值的概率直方圖進行函數擬合，得到對應的概率密度函數f(x)：

豎向溫度梯度模式中腹板頂部日極值正溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝5.13，σ＝3.50，如圖24所示；

豎向溫度梯度模式中距腹板頂部0.2m處折點日極值正溫差標準值t2符合正態分布，其概率密度函數為：

式中μ＝3.30，σ＝1.00，如圖25所示；

豎向溫度梯度模式中腹板頂部日極值負溫差標準值t1符合極值ⅰ型分布，其概率密度函數為：

式中μ＝-1.26，σ＝0.62，如圖26所示；

橫向溫度梯度模式中距兩側腹板1.4m處日極值正溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝2.56，σ＝0.88，如圖27所示；

橫向溫度梯度模式中腹板頂部日極值負溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝-1.46，σ＝0.85，如圖28所示；

6、通過概率密度函數f(x)，計算設計基準期為100年，不同重現期n的溫差標準值t。

概率密度函數f(x)所對應的分布函數為fx(x)，則設計基準期100年內的頂板和各個折點的極值溫差值的累積分布函數fy(x)為：fy(x)＝[fx(x)]¹⁰⁰；

溫差標準值的保證率為p0，對鐵路鋼箱梁橋施工期溫度設計標準值進行取值，可將兩年作為施工期設計基準期，分別取半年、一年作為施工期溫度作用重現期，則施工期內極值溫差作用的溫差標準值的保證率分別為96％、98％；

令fy(x)＝p0，計算得x為溫差標準值t。

混凝土鋪裝鋼箱梁豎向溫差標準值見表1，橫向溫差標準值見表2。

7、為方便在實際工程中的應用，對不同重現期混凝土鋪裝鐵路鋼箱梁的溫差標準值進行偏安全取整，得到溫差標準值的建議值。

混凝土鋪裝鐵路鋼箱梁豎向溫差標準值的建議值見表3，橫向溫差標準值的建議值見表4。

實施例3

1、在道砟層鋪裝鋼箱梁橋腹板和頂板上布置溫度測點并采集溫度，每次采集時間間隔為3分鐘；每次采集時間間隔也可為2分鐘，每次采集時間間隔還可為5分鐘；

參照英國規范bs-5400對鋼橋溫度梯度的規定，在道砟鋪裝層鋼箱梁兩側腹板布置溫度測點，溫度測點位置以距頂板的垂直距離表示為0.0m，0.05m，0.1m，0.2m，0.3m，0.6m，1.2m，2.4m，4.15m和腹板底部；在頂板布置溫度測點，溫度測點位置以距離右側腹板的水平距離表示為：0.0m，1.4m，2.8m，4.2m；每隔3分鐘采集一次各測點溫度并記錄。

2、將采集獲得的混凝土鋪裝層鋼箱梁橋溫度進行分析，找出腹板各測點日極值溫差值所對應時刻的溫度數據，以溫度為橫坐標，測點間的距離為縱坐標，作出梯度散點圖，并采用最小二乘法進行曲線擬合。

在距腹板頂部2.4m范圍內采用非線性擬合，得到豎向正溫度梯度曲線，如圖13所示；在距腹板頂部2.4m范圍內采用非線性擬合，得到豎向負溫度梯度曲線，如圖14所示；頂板上距右側腹板1.4m至2.8m處的溫度較高采用線性擬合，距右側腹板0.0m處測點和4.2m處測點的溫度較低且相近，得到呈梯形的橫向正溫度梯度曲線，如圖17所示；頂板上距右側腹板1.4m至2.8m處的溫度較低采用線性擬合，頂板與陰面腹板相交處溫度次之，頂板與陽面腹板相交處溫度最高，得到呈線性的橫向負溫度梯度曲線，如圖18所示。

3、將得到的溫度梯度曲線簡化成折線，為溫度梯度模式；

對豎向正溫度梯度曲線簡化，在距腹板頂部0.05m范圍內采用直線簡化，在距腹板頂部0.05m到2.4m范圍內采用直線簡化，0.05m處為折點，得到豎向正溫度梯度模式如圖15所示；

對豎向負梯度曲線簡化，在距腹板頂部2.4m范圍內采用直線簡化，得到豎向負溫度梯度模式如圖16所示；

橫向正負溫度梯度曲線均為折線形，不需要簡化。

4、得到豎向溫度梯度模式腹板各折點的日極值溫差值和橫向溫度梯度模式頂板各折點的日極值溫差值；

腹板各折點日極值溫差值為各折點處測點溫度值減去腹板測點最低溫度值，頂板各折點的日極值溫差值為頂板各折點處測點溫度值減去頂板測點最低溫度值；

5、對鋼箱梁橋的頂板和腹板各個折點的日極值溫差值進行統計分析，得到溫差概率分布直方圖，再對直方圖進行概率擬合，得到日極值溫差概率密度函數；

統計頂板和腹板各個折點的日極值溫差值并輸入到計算機，應用origin8.0數理統計分析軟件分別做出頂板和腹板各個折點的日極值溫差值的概率直方圖，再分別對頂板和腹板各個折點的日極值溫差值的概率直方圖進行函數擬合，得到對應的概率密度函數f(x)：

豎向溫度梯度模式中腹板頂部日極值正溫差標準值t1符合極值ⅰ型分布，其概率密度函數為：

式中μ＝2.58，σ＝1.17，如圖29所示；

豎向溫度梯度模式中距腹板頂部0.05m處折點日極值正溫差標準值t2符合正態分布，其概率密度函數為：

式中μ＝2.20，σ＝1.35，如圖30所示；

豎向溫度梯度模式中腹板頂部日極值負溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝-2.52，σ＝2.24，如圖31所示；

橫向溫度梯度模式中距兩側腹板1.4m處日極值正溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝1.00，σ＝0.70，如圖32所示；

橫向溫度梯度模式中距兩側腹板1.4m處日極值負溫差標準值t1符合正態分布，其概率密度函數為：

式中μ＝-1.87，σ＝0.94，如圖33所示；

橫向溫度梯度模式中腹板頂部日極值負溫差標準值t2符合正態分布，其概率密度函數為：

式中μ＝-0.60，σ＝0.33，如圖34所示；

6、通過概率密度函數f(x)，計算設計基準期為100年，不同重現期n的溫差標準值t；

概率密度函數f(x)所對應的分布函數為fx(x)，則設計基準期100年內的頂板和各個折點的極值溫差值的累積分布函數fy(x)為：fy(x)＝[fx(x)]¹⁰⁰

溫差標準值的保證率為p0，對鐵路鋼箱梁橋施工期溫度設計標準值進行取值，可將兩年作為施工期設計基準期，分別取半年、一年作為施工期溫度作用重現期，則施工期內極值溫差作用的溫差標準值的保證率分別為96％、98％；

令fy(x)＝p0，計算得x為溫差標準值t。

道砟層鋪裝鋼箱梁豎向溫差標準值見表1，橫向溫差標準值見表2。

7、為方便在實際工程中的應用，對不同重現期道砟層鋪裝鐵路鋼箱梁的溫差標準值進行偏安全取整，得到溫差標準值的建議值。

道砟層鋪裝鐵路鋼箱梁豎向溫差標準值的建議值見表3，橫向溫差標準值的建議值見表4。

表1鐵路鋼箱梁豎向溫差標準值

表2鐵路鋼箱梁橫向溫差標準值

表3鐵路鋼箱梁豎向溫差標準值的建議值

表4鐵路鋼箱梁橫向溫差標準值的建議值