一種工件三維點云數據平滑濾波方法與流程

本發明涉及一種工件三維點云數據處理的方法，具體說是一種工件三維點云數據平滑濾波方法。可以結合機器人應用于工業領域，獲取工件的相關信息，屬于工業機器人視覺應用領域。
背景技術：
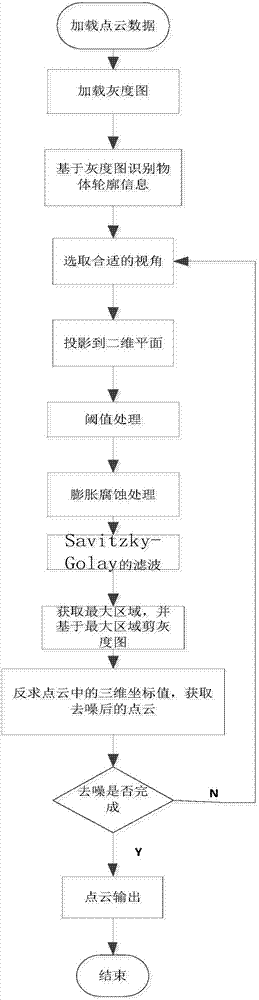
：視覺系統配合機器人，成為“手眼系統”。在現代智能工業應用中，利用“手眼系統”代替產線工人完成生產線流水作業、產線裝配，或者利用視覺系統完成物料的測量、質量檢查等繁瑣工作，提高機器人對環境的感知與應變能力，利用機器人的視覺控制，不需要預先對工業機器人的運動軌跡進行示教或離線編程，可節約大量的編程時間，提高生產效率和加工質量，在一定程度上將人工從生產勞動中解放出來。立體視覺是計算機視覺領域的一個重要課題，它的目的在于重構場景的三維幾何信息。立體視覺的研究具有重要的應用價值，其應用包括移動機器人的自主導航系統，航空及遙感測量，工業自動化系統等。基于傳感器獲取三維信息的方法有很多種，主要分為主動式和被動式，工業領域一般采用主動式三維方式獲取深度信息，即通過打結構光或者光編碼等方式獲取立體深度信息，此立體深度信息亦成為三維點云信息。獲取三維點云數據之后，需要對點云數據進行濾波處理。目前的點云濾波算法主要有：lidar數據形態學濾波算法、基于坡度變化的濾波算法等。lidar數據形態學濾波算法主要問題是坡度閾值的人工選取和細節地形的方塊效應，如果閾值設定太大，可能平滑掉噪聲，同時將工件的細節平滑處理，算法的普遍適用性很差。基于坡度變化的濾波算法原理是根據工件輪廓確定最優的濾波函數，雖然算法簡單，但是需要提前知道工件的輪廓變化信息以及設定的窗口信息，算法適用性差。技術實現要素：本發明的目的在于，克服現有技術存在的缺陷，提供一種工件三維點云數據平滑濾波方法。本發明方法基于savitzky-golay濾波，消除原始數據的不光滑，提高點云處理數據的質量，能更真實反映出物體的本來面貌。本發明一種工件三維點云數據平滑濾波方法，包含以下步驟：步驟1：采集工件的點云數據基于工件的形狀，選取一個視角，采集工件的三維輪廓點云數據。步驟2:將采集的工件點云數據按照點的三維坐標值獲取對應的灰度圖，并將點云投影到視平面上面。步驟3：得到投影的灰度圖，并對灰度圖進行二值化閾值處理,得到二值圖。步驟4：對二值圖進行開閉合運算。步驟5：用savitzky-golay濾波去除圖像的噪聲1)確定m和n的值。n表示領域內的點個數，m表示多項式的次數。n取值相同，m值越小，平滑效果越好，但是為了確保濾波后的點云和原點云差別不大，一般取m＝3。m相同，n越大，細節丟失越大，因此通過曲率的相關關系確定m和n的值。(1)利用m次樣條插值計算點云的曲率ci(i＝1,2,...,n)以及曲率導數dci(i＝1,2,...,n-1)，n表示點云的總數。(2)令nmax＝n/4,nmin＝5；若滿足(n/4)＜5，則n＝5，若點云數n小于5，則結束處理。(3)確定n的值；若某點的曲率值ci＜q1，那么可以認為這點和其領域點在一條直線上，然后在其領域內尋找滿足dci＜q2的點，確定點后，如果n1＞n2，則n＝2n1+1；否則：n＝2n2+1，若某點的曲率值ci＞q1，則該點曲率變化dci在其領域內尋找滿足或者的點，其中其中q，q1，q2為曲率分割閾值的經驗值，如果n1＞n2，則n＝2n1+1；否者：n＝2n2+1，確定n和m的值。n1表示曲率小于并接近q2的點個數，n2表示曲率值大于并接近q2的點個數。2)確定n和m的值之后，用savitzky-golay濾波器去除圖像的噪聲對任意點xi領域內的n個點用m階多項式進行擬合，運用最小二乘則確定多項式的系數，多項式在xi處的值是對應點的光滑值gi；n要大于多項式的階數m；由掃描數據xi擬合的m次多項式pi(x)表示為：其中x表示n個點云中除了點xi外的任意一點。假設對于任意xi都有xi+1-xi＝δx，擬合多項式需要計算出(1-1)中的系數bk，使其達到最優，即：bk的系數的矩陣表達：其他參數用向量表示為：和y表示濾波值，yi，分別點i+n1、點i、點i+n2的濾波值。由式(1-3)和(1-4)，式(1-2)可寫為：式(1-5)可以表示為：atabk＝aty(1-6)因為ata是正定矩陣，且存在逆矩陣，系數bk：bk＝(ata)-1aty(1-7)步驟6：用分水嶺分割識別法進行區域分割識別，將圖像區域劃分成幾個部分，獲取最大的區域，基于最大區域裁剪的彩色圖，得到去噪后的彩色圖。步驟7：根據彩色圖中的點反推算點云數據中個點的三維坐標值，得到去噪后的點云。步驟8：判斷點云數據中噪音情況，如果有，換視角，再次濾波，如果沒有，輸出結果，本發明相較于其它算法的優點：1.保持幾何特征不變(算法濾波處理，采用擬合算法處理，去除圖像中的噪聲，保持工件的幾何特征不變)；2.精度和速度比其它算子高；(基于灰度圖，獲取鑄件的點云數據，數據運算量減少，加快了數據的處理速度，采用擬合計算的方法，提供點云計算的精度。)3.適用性強(數據擬合計算，適用于不同的鑄件，適應性強)。附圖說明圖1是savitzky-golay算法的流程圖。圖2是本發明工件三維點云數據平滑濾波方法程序框圖。圖3是工件樣本灰度圖。圖4是savitzky-golay濾波前的效果圖。圖5是savitzky-golay濾波后的效果圖。具體實施方式下面結合附圖和實施例，對本發明作進一步詳細說明。實施例，本發明以鐵管鑄件為工件，具體介紹本發明提出的工件三維點云數據平滑濾波方法，如圖2所示，具體實施過程如下：步驟1：加載工件的點云數據，在vs2013軟件平臺上上利用vc讀取鐵管鑄件的點云數據。步驟2：擇一個投影方向，調用pcl(pointcloudlibrary)點云算法庫，采用貪婪投影三角化方法，計算點云法向量，并將法向量和點云坐標放在一起，確定點云投影的角度和方向。步驟3：加載灰度圖，如圖3。在vs2013軟件平臺上加載讀取灰度圖，并對灰度圖進行二值化處理。步驟4：用圓形結構對二值圖像進行先膨脹后腐蝕的開合閉運算。以3為半徑，創建圓形結構，利用圓形結構對二值圖進行腐蝕處理，再利用圓形結構對腐蝕后的圖像進行膨脹處理，得到處理后的二值圖，確定需要處理的數據區域。步驟5：用savitzky-golay濾波去除圖像的噪聲。采用savitzky-golay濾波首先需要確認幾個參數：多項式的擬合次數m，點xi領域內的總點數n，點xi兩邊的點數n1和n2。為了使計算的精度和速度達到較好的水平，m一般取2,3，4。本實施例m＝3，n不能設置太大，否則影響處理數據的速度，但又不能影響擬合的精度，且n為基數，因此設置設n的值為47。基于各方向上矢量值一致性原則，令n1＝n2。確定n和m的值之后，用savitzky-golay濾波器去除圖像的噪聲：對任意點xi領域內的n＝47個點用m＝3階多項式進行擬合，運用最小二乘則確定多項式的系數，多項式在xi處的值是對應點的光滑值gi。由掃描數據xi擬合的m＝3次多項式pi(x)可表示為：假設對于任意xi都有xi+1-xi＝δx，擬合多項式需要計算出(1-1)中的系數bk，使其達到最優，即：bk的系數的矩陣表達：其他參數用向量表示為：和由式(1-3)和(1-4)，式(1-2)可寫為：式(1-5)可以表示為：atabk＝aty(1-6)因為ata是正定矩陣，且存在逆矩陣，系數bk：bk＝(ata)-1aty(1-7)圖4濾波后的效果圖為圖5。步驟6：用分水嶺分割識別法進行區域分割識別，將圖像區域劃分成幾個部分，獲取最大的區域，處理濾波后的圖，獲取最大有效區域。步驟7：根據灰度圖中的點反推算點云數據中個點的三維坐標值，得到去噪后的點云。反求點云的三維坐標，獲取去噪后的點云。步驟8：判定去噪是否合格。如果合格，輸出點云，如果不合格，則再次選擇一個可以清物體輪廓的角度，再次濾波。表1體現了本文算法與常用的閾值濾波算法在時間上的比較。表1點云數據量閾值濾波平均花費的時間(s)本文算法的平均花費的時間(s)19420124301990135081317980061250240190158033450387實驗數據在cpu為3.0ghz，內存為4g,系統為win7的pc上獲取。當前第1頁12