一種基于混合Copula函數的多風場出力預測方法與流程

本發明涉及一種基于混合copula函數的多風場出力預測方法，屬于電氣工程技術領域。

背景技術：

風能作為目前使用最廣泛的可持續新資源之一，其資源開發具有集中式、連片式的特點。由于地域和氣候的相似性，一定區域內的風電場風電出力之間具有很強的相關性。由于這種相關性會影響電力系統安全穩定運行而受到越來越多的研究者的重視。

在實際系統運行過程中，通過分析風電場出力的隨機特性，構建典型風電出力場景，針對典型場景制定應對風功率隨機變化的措施，是求解含風電電力系統優化運行問題的一種重要手段。

傳統的風電出力預測模型中假定并網風電的預測誤差服從正態分布，雖然符合統計學規律，但沒有考慮并網之前多風場之間的相關性。當并網風電是從兩個或多個區域風電場合并得到時，各風場出力是具有時空上的相關性的。相同區域內的風電場風出力之間存在較強的相關性，而傳統的風場出力預測方法并沒有考慮相關性。

技術實現要素：

針對現有技術的不足，本發明提出了一種基于混合copula函數的多風場出力預測方法，其能夠有效解決地域上具有相關性的多風場并網出力預測問題。

本發明解決其技術問題采取的技術方案是：一種基于混合copula函數的多風場出力預測方法，其特征是，包括以下步驟：

1)構建混合copula函數模型；

2)模型選擇和參數估計；

3)具有相關性的多風場出力預測。

進一步地，在步驟1)中，所述的混合copula函數模型為：

其中，ck(u1,u2；θk)為已知的copula函數，u1,u2為隨機變量，θk為相依參數，λk為權重系數，滿足0≤λk≤1，k＝4，已知的copula函數包括gauss-copula函數、frank-copula函數、gumbel-copula函數和clayton-copula函數。

進一步地，在步驟2)中，模型選擇和參數估計的過程包括以下步驟：首先構建懲罰似然函數，其次對邊緣分布的估計，然后對混合copula函數中的權重參數和相依參數進行估計，最后采用交叉驗證法來對γ和α進行估計。

進一步地，所述構建懲罰似然函數的過程為：

假設二維隨機變量(x，y)的邊緣分布為x～fx(x；α)，y～gy(y；β)，且其混合copula函數為則(x，y)的聯合分布為：

其中，

則(x，y)的密度函數為：

其中，

在得到參數φ的估計值之前，首先求出(x，y)的極大似然函數：

其中，fx(xi；α)和gy(yi；β)為邊緣密度函數；(xn，yn)為來自(x，y)的樣本，n＝1,2,…,n，n為樣本容量；

構建的懲罰似然函數為：

其中，{pγt}是光滑參數，控制模型的復雜性。

進一步地，所述對邊緣分布的估計的過程就是對采用非參數核密度估計，得到密度函數的估計值和從而得到邊緣分布函數的估計值和

所述對混合copula函數中的權重參數和相依參數進行估計的過程為：把邊緣分布函數的估計值代入二元gauss-copula的概率密度函數，得到：

并采用em算法來估計(λk，θk)。

進一步地，所述非參數核密度估計為：

設k¹(·)為r¹上的一個給定概率密度函數。hm>0是一個與m有關的常數，滿足n→∞，hm→0，則稱

為f(x)的一個核密度估計，其中，k¹(·)為核函數，hm稱為窗寬或光滑參數。

進一步地，所述采用em算法來估計(λk，θk)的過程為：

e步，求期望：給定觀測數據x和當前系數估計值，計算完全數據的對數似然函數lnp(x,y|θ)關于未知數據y的條件期望分布，即：

其中，θ^i-1為已知的當前系數的估計值；

m步，求極大值：將q(θ|θ^i-1,y)關于θ極大化，即找一個θⁱ點，使得

從而形成了一次迭代θⁱ→θ^i-1；

最后將上述e步和m步進行迭代直至||θⁱ-θ^i-1||或||q(θⁱ|θ^i-1,y)-q(θ^i-1|θ^i-1,y)||充分小為止。

進一步地，在采用em算法來估計(λk，θk)的過程需要用到而該式沒有顯式表達形式，采用擬牛頓法中的bfgs算法來得到θ的更新方程；

設采用擬牛頓法中的bfgs算法來得到θ的更新方程的具體過程包括以下步驟：

step1：給定初始點θ¹，允許誤差ε>0；

step2：設矩陣h1＝ik(k階單位矩陣)，計算出在θ¹處的梯度置i＝1；

step3：令迭代方向dⁱ＝-higi；

step4：從θⁱ出發，沿著方向dⁱ進行線性搜索，使它滿足令θⁱ⁺¹＝θⁱ+αidⁱ；

step5：檢驗是否滿足收斂準則，若則停止迭代，得到近似解θ＝θⁱ⁺¹，否則，進行step6；

step6：若i＝k，則令θ¹＝θⁱ⁺¹，返回進行step2，否則進行step7；

step7：令pⁱ＝θⁱ⁺¹-θⁱ，qⁱ＝gi+1-gi，同時令

置i＝i+1，返回step3。

進一步地，所述采用交叉驗證法來對γ和α進行估計的過程為：

設d為完整的數據集，把完整的數據分成m分，di，i＝1,2,…,m，把di作為檢驗集，d-di作為交叉驗證訓練集；對任意給定罰函數的參數(γ，α)，先首先采用d-di的數據，通過上面的em算法分別得到權重系數λ和相依系數θ的估計值然后計算選擇使得下式最大的光滑參數：最后得出(γ，α)的估計值

進一步地，在步驟3)中，具有相關性的多風場出力預測的具體過程為：

設兩相鄰風電場一天t＝96個時段的風電出力為隨機變量，即t組相關的二元隨機變量(u11，u21),(u12，u22)，…，(u1t，u2t)，通過對其進行分析確定混合copula函數的各項參數；

所述確定混合copula函數的各項參數的過程包括以下步驟：首先，對混合copula函數的擬合效果進行檢驗；然后，用mc法產生服從各copula函數的隨機變量的概率；最后，對以上隨機變量進行累積分布逆變換，即非參數核密度估計，從而生成服從風電場出力聯合分布的預測結果。

本發明的有益效果如下：

本發明通過結合4種copula函數構建混合copula函數模型，提出了一種基于混合copula函數的多風場出力預測方法，它對相同區域內的風電場風出力之間存在較強的相關性進行分析，解決了地域上具有相關性的多風場并網出力預測問題。

本發明結合4種copula函數構建混合copula函數模型，其擬合精度優于單一copula函數，對相同區域內的風電場風出力之間存在較強的相關性進行分析，在應用于調度時有利于風電的消納。當風電采用多風場并網的方式時，采用本發明提出的多風場出力預測方法不僅優于假設預測場景的誤差分布呈正態分布的出力預測方法，而且在并網調度時更有利于系統對風電的消納。

附圖說明

圖1為本發明的方法流程圖；

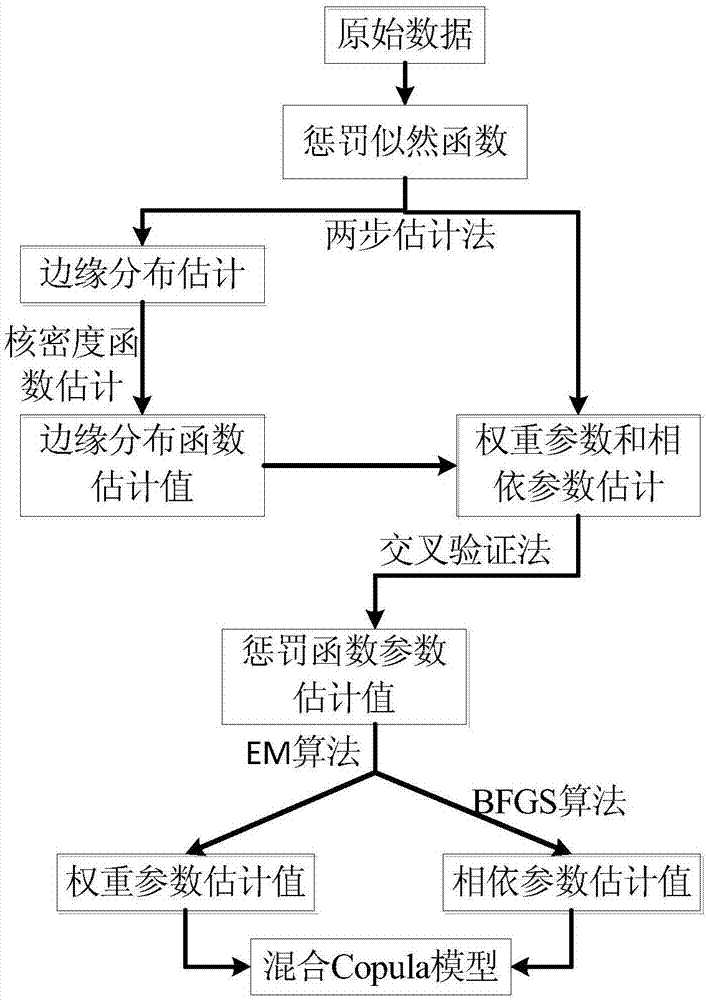
圖2為本發明的模型選擇和參數估計流程圖；

圖3為本發明算例中第一組預測場景風電出力的數據曲線圖；

圖4為本發明算例中第二組預測場景風電出力的數據曲線圖。

具體實施方式

為能清楚說明本方案的技術特點，下面通過具體實施方式，并結合其附圖，對本發明進行詳細闡述。下文的公開提供了許多不同的實施例或例子用來實現本發明的不同結構。為了簡化本發明的公開，下文中對特定例子的部件和設置進行描述。此外，本發明可以在不同例子中重復參考數字和/或字母。這種重復是為了簡化和清楚的目的，其本身不指示所討論各種實施例和/或設置之間的關系。應當注意，在附圖中所圖示的部件不一定按比例繪制。本發明省略了對公知組件和處理技術及工藝的描述以避免不必要地限制本發明。

如圖1所示，本發明的一種基于混合copula函數的多風場出力預測方法，它包括以下步驟：

1)構建混合copula函數模型；

2)模型選擇和參數估計；

3)具有相關性的多風場出力預測。

在步驟1)中，混合copula函數模型描述如下：

不同類型的copula函數描述變量相關性的側重點不同。gauss-copula函數和frank-copula函數適合描述數據間的對稱相關性；gumbel-copula函數刻畫了非對稱的上尾相關性，clayton-copula函數刻畫了非對稱的下尾相關性。這樣如果在實際應用中只用某一種copula函數來擬合數據，可能會出現失真的情況。由于不同的copula函數對相關性描述的側重點不同，因此考慮把這幾種copula函數混合在一起，這樣混合copula函數就能更好地描述數據間的相關性，更好地融合數據。二元混合copula的函數模型如下：

其中，為已知的copula函數，θk為相依參數，λk為權重系數，滿足0≤λk≤1，且混合copula函數仍是copula函數。

在步驟2)中，如圖2所示，混合copula函數模型的模型選擇和參數估計流程如下：

這一步要解決的是混合copula函數的模型選擇和參數估計問題。利用懲罰似然函數對混合copula函數進行模型選擇和參數估計，選擇和估計的步驟分為兩步：首先就是對邊緣分布的估計，本文引入非參數中核密度估計對邊緣分布進行參數估計；接著就是對混合copula函數中的權重參數和相依參數進行估計。由于懲罰似然函數中涉及到多重求和的函數形式，對其最大化比較困難，故采用em(expectation&maximization)算法^[101]進行處理。其中，對em算法中m步，利用最優化方法中的bfgs^[102]算法進行解決，從而完成對混合copula函數的模型選擇和參數估計。

1、懲罰似然函數

假設二維隨機變量(x，y)，設其邊緣分布為x～fx(x；α)，y～gy(y；β)，且設其混合copula函數為則的聯合分布為(x，y)為：

其中，則可知(x，y)的密度函數為：

其中，

想要得到參數φ的估計值，首先求出(x，y)的極大似然函數，即：

其中，fx(xi；α)和gy(yi；β)為邊緣密度函數；(xn，yn)，n＝1,2,…,n。為來自(x，y)的樣本，n為樣本容量。

如果只是對求得的極大似然函數進行估計的話，可能會把不顯著的copula函數(相關性描述不顯著)選進去，這樣會造成模型失真。這其實是一個模型選擇的問題，因此，通過引入懲罰函數來對權重參數進行懲罰選擇。這樣可以利用懲罰函數把一些不顯著的copula函數剔除，從而可以使模型更好地擬合數據。為此構建懲罰似然函數：

其中，{pγt}是光滑參數，控制模型的復雜性。本節對各個權重的懲罰函數均采用scad懲罰(smoothlyclippedabsolutedeviationpenalty)函數，該函數滿足一個好的懲罰函數需要具有的無偏性、稀疏性和連續性，三個性質。

2、兩步估計懲罰函數

對二元gauss-copula的概率密度函數參數的估計，可以分成兩步。首先就是對邊緣分布的參數進行估計，然后對混合copula函數的權重參數及相依參數進行估計。具體步驟如下：

第一步：

對采用非參數核密度估計，得到密度函數的估計值從而得到邊緣分布函數的估計值

第二步：

把邊緣分布函數的估計值代入二元gauss-copula的概率密度函數，得到：

對阿基米德copula的概率密度函數采用em法來估計(λk，θk)。

(1)邊緣分布的核密度估計

從對邊緣分布的估計，有學者采用經驗分布對邊緣分布進行估計，然而經驗分布一般不連續或光滑性不夠，用來表述邊緣分布會產生較大的誤差。還有的學者就直接假設其分布，然后去驗證。然而采用這種方法會使得驗證步驟變得繁瑣，所以具有一定局限性。對此，本發明采用非參數的方法，即，核密度估計來對邊緣分布進行估計，從而實現用數據來擬合邊緣分布，使模型更加真實。

非參數核密度估計是由rosenblatt和parzen提出的，下面給出核密度估計的定義：

設k¹(·)為r¹上的一個給定概率密度函數。hm>0是一個與m有關的常數，滿足n→∞，hm→0，則稱

為f(x)的一個核密度估計。其中，k¹(·)為核函數，hm稱為窗寬或光滑參數。本發明采用高斯核，窗寬采用經驗法則^[104]：具體為ksdensity/matlab函數。

(2)em算法

這樣在邊緣分布利用非參數核密度估計估計出邊緣分布函數后，接下來要估計的是混合copula的權重系數和相依系數。由于混合copula的極大似然函數很復雜，無法用求偏導的方法進行解決，因此本發明采用em算法來解決此問題。

em算法是一種迭代算法，由dempster.laird和rubin于1977年提出的。它可廣泛地應用于不完全數據，如缺損數據、截尾數據、成群數據、帶有討厭參數的數據。em算法主要有兩步：第一步，求期望，即e步；第二步，求極大值，即m步。具體地講：

e步：給定觀測數據x和當前系數估計值，計算完全數據的對數似然函數lnp(x,y|θ)關于未知數據y的條件期望分布，即：

其中，θ^i-1為已知的當前系數的估計值。

m步：將q(θ|θ^i-1,y)關于θ極大化，即找一個θⁱ點，使得

從而形成了一次迭代θⁱ→θ^i-1。將上述e步和m步進行迭代直至||θⁱ-θ^i-1||或||q(θⁱ|θ^i-1,y)-q(θ^i-1|θ^i-1,y)||充分小為止。

在用em法解決二元copula概率密度函數參數估計的過程中需要用到而該式沒有顯式表達形式，所以采用擬牛頓法中的bfgs算法來解決。

(3)bfgs算法

bfgs算法是擬牛頓法中的一種應用較為廣泛的解決非線性優化問題的算法。其主要是在牛頓法的基礎上進行改進。由于牛頓法中需要計算二階偏導數而且要求目標函數的hesse矩陣為對稱正定矩陣，這些條件較為苛刻。因此對牛頓法進行改進，學者們提出擬牛頓法。擬牛頓法主要是根據taylor公式的近似展開式得到的擬牛頓方程來構造矩陣，以此來近似hesse矩陣或其逆矩陣，并求得迭代方向。由于構造矩陣的方法不同，從而出現不同的擬牛頓法，本發明采用由broyden，foldfarb和shanno于1970年提出的bfgs算法。

設下面具體給出bfgs算法的計算步驟：

step1：給定初始點θ¹，允許誤差ε>0。

step2：設矩陣h1＝ik(k階單位矩陣)，計算出在θ¹處的梯度置i＝1。

step3：令迭代方向dⁱ＝-higi。

step4：從θⁱ出發，沿著方向dⁱ進行線性搜索，使它滿足令θⁱ⁺¹＝θⁱ+αidⁱ(更新方程)。

step5：檢驗是否滿足收斂準則，若則停止迭代，得到近似解θ＝θⁱ⁺¹，否則，進行step6。

step6：若i＝k，則令θ¹＝θⁱ⁺¹，返回進行step2，否則進行step7。

step7：令pⁱ＝θⁱ⁺¹-θⁱ，qⁱ＝gi+1-gi，同時令

置i＝i+1，返回step3。這樣通過bfgs算法可以得到θ的更新方程。

通過上面em算法和bfgs算法的結合可以得到權重系數λ＝(λ1,...,λk)^t和相依系數θ＝(θ1,...,θk)^t的估計值。在上面的估計過程中要用到scad懲罰函數中的光滑參數γ和α。下面采用交叉驗證法來對γ和α進行估計。

(4)交叉驗證法

交叉驗證法一般是采用平均平方誤差準則，其基本原理就是把數據分為兩部分：第一部分作為檢測集用來預測(或檢驗)，第二部分作為訓練集用來進行估計。具體如下：

設d為完整的數據集，把完整的數據分成m分，di(i＝1,2,…,m)。這里把di作為檢驗集，d-di作為交叉驗證訓練集。對任意給定罰函數的參數(γ，α)，先首先采用d-di的數據，通過上面的em算法分別得到權重系數λ和相依系數θ的估計值然后計算選擇使得下式最大的光滑參數：這樣得出(γ，α)的估計值后，繼續利用前面的em算法對完整數據集d進行參數估計得出權重系數及相依系數的估計值。

在步驟3)中，具有相關性的多風場出力預測表述如下：

設兩相鄰風電場一天t＝96個時段的風電出力為隨機變量，即t組相關的二元隨機變量(u11，u21),(u12，u22)，…，(u1t，u2t)。對其進行分析，確定混合copula函數的各項參數。首先，對混合copula函數的擬合效果進行檢驗。然后，用mc法產生服從各copula函數的隨機變量的概率，可調用matlab中的copularnd函數生成。最后，對以上隨機變量進行累積分布逆變換，即非參數核密度估計，可調用matlab中的ksdensity函數生成。從而生成服從風電場出力聯合分布的預測結果。

下面通過算例來驗證本發明對兩個風場出力進行預測的情況。

(1)第一組風電數據，兩風電場大約相距80公里。風電場一最大出力為422mw，風電場二最大出力為472mw，并網最大出力為860mw。圖3為第一組預測場景風電出力曲線圖，表1為第一組數據下不同copula函數的對比。

表1第一組數據下不同copula函數的對比

由表1可以看出，第一組數據中兩風場出力的相關性最符合clayton-copula分布；混合copula函數權重系數λ3＝1，其余為零。擬合效果相同，選擇完全服從clayton-copula分布。

(2)第二組風電數據，兩風電場大約相距40公里。風電場一最大出力為615mw，風電場二最大出力為538mw，并網最大出力為1050mw。圖4為第二組預測場景風電出力曲線圖，表2為第二組數據下不同copula函數的對比。

表2第二組數據下不同copula函數的對比

由表2可以看出，混合copula函數權重系數λ3＝0.5351，λ4＝0.4649，其余為零。對第二組數據的擬合效果優于用幾種copula單獨擬合得到的結果。綜上，混合copula得到的擬合數據總是優于(至少不弱于)幾種copula單獨擬合得到的結果。

以上所述只是本發明的優選實施方式，對于本技術領域的普通技術人員來說，在不脫離本發明原理的前提下，還可以做出若干改進和潤飾，這些改進和潤飾也被視為本發明的保護范圍。