一種基于結構特征描述的三維幾何模型去噪方法與流程

本發明涉及一種基于結構特征描述的三維幾何模型去噪方法。

背景技術：

隨著數字化掃描技術的普及，獲取大規模測量點所重建的三維幾何模型已經被越來越多的領域廣泛應用，如影視娛樂、虛擬現實、醫療診斷、工業制造、文物保護等。由于數字化設備精度誤差、三維重建方法缺陷及一些人為因素等，獲得的模型不可避免地存在各種噪聲和擾動，它們的存在十分不利于顯示傳輸及其他后續幾何處理和分析操作，如幾何模型參數化、三維水印、網格變形等，因此需要對獲取的幾何模型進行去噪處理。

幾何模型去噪早期的工作主要有基于拉普拉斯的光順、基于曲率流的擴散以及基于頻率域的濾波等方法。這些方法雖然能夠很好的去除模型的噪聲，但是由于在去噪過程中未將特征和噪聲進行區分，很容易產生過光順而將幾何模型的一些特征去除。為了在剔除幾何模型噪聲的同時保持固有的幾何特征，本領域技術人員提出了一些能夠保持幾何模型特征的各向異性的平滑方法，諸如基于雙邊濾波的去噪、基于各向異性擴散的光順算法、基于全變分優化的去噪、基于壓縮感知的去噪等。然而，現有的局部迭代的幾何模型去噪方法一般不能保證結果的收斂性，比較容易出現幾何模型體積收縮現象，整體優化的去噪方法通常需要將原始模型信息作為約束，容易將噪聲看作特征而不能很好的去噪，而且對于大規模幾何模型的處理速度較慢。

技術實現要素：

本發明的目的是為了降低噪聲的同時保持輸入幾何模型的尖銳特征，提供一種基于結構特征描述的三維幾何模型去噪方法，它從幾何信號的角度出發，構建一種有效的幾何結構特征描述子，并將其融入在非局部均值濾波框架中進行幾何模型去噪，防止幾何模型的體積收縮，提高去噪的有效性和魯棒性。

本發明的目的是通過以下技術方案來實現的：一種基于結構特征描述的三維幾何模型去噪方法，其特征是，它包括以下步驟：

1)幾何信號的構建

對于以三角網格表示的三維幾何模型，通過幾何模型頂點的拉普拉斯算子和頂點法向進行內積構建幾何信號，該信號能夠刻畫幾何模型的局部細節特征；

2)基于法向張量的結構特征描述子的計算

通過頂點法向張量的所有特征值的和以及最小單位特征向量作為結構特征測度描述子，該描述子能夠刻畫幾何模型上角點、邊點和面點的特征信息；

3)幾何信號的非局部均值濾波

通過各頂點相互之間結構特征測度描述子的差異作為非局部均值濾波的權值計算依據，對頂點的離散拉普拉斯算子與對應頂點法向量內積所得的幾何模型上信號進行非局部均值濾波，得到一個新的幾何信號；

4)幾何模型重建

將原始幾何模型頂點作為約束條件，通過將步驟3)所得的濾波后新的幾何信號進行拉普拉斯曲面重建，得到非局部均值濾波后信號對應的幾何模型；

所述步驟1)中幾何信號的構造的具體實現為：

設{vi|i＝1,2,…,n}為以三角網格表示的三維幾何模型的n個頂點，δ(vi)為頂點vi的離散拉普拉斯算子，頂點法向量為ni，將幾何信號定義為兩者內積形式為(1)式：

si＝(δ(vi),ni)(1)

對于幾何模型上所有頂點的幾何信號，可以寫成(2)式的矩陣形式：

lv＝sn(2)

其中v表示幾何模型頂點的位置向量矩陣，s＝diag(s1,s2,…,sn)表示以頂點信號si作為對角線元素的矩陣，n為頂點的法向矩陣，l為幾何模型的拉普拉斯矩陣，具有(3)式形式：

其中wij＝cotαij+cotβij，αij,βij是頂點vi與vj連線所成的邊所對的兩個角，n(i)是頂點vi的一環鄰域點集。

所述步驟2)中基于法向張量的結構特征描述子的計算具體實現為：

對于給定的幾何模型頂點vi，其法向張量可由它周圍的三角面片的單位法向量定義為(4)式：

其中f(vi)表示頂點vi周圍的三角形的指標集合，為(5)式的權重系數：

a(fk)是三角形fk的面積，amax是頂點vi周圍的三角形的最大面積，是三角形fk重心；

由于法向張量為三階對稱半正定矩陣，可以求出其特征值λ1≥λ2≥λ3≥0和所對應的單位特征向量e1,e2,e3，由于幾何模型上角點、邊點和面點所對應的特征值有明顯的差距，而且最小特征向量的方向e3對應著頂點的特征方向，采用(6)式的度量作為頂點結構特征測度描述子：

des(vi)＝{di,ti}(6)

其中di＝λ1+λ2+λ3，ti對應頂點法向張量的最小特征向量；

在此基礎上，通過(7)式如下度量來計算各頂點之間結構特征描述子的差異：

d(vi,vj)＝(di-dj)²+(1-|(tj,ti)|)(7)

其中(tj,ti)表示頂點特征方向的內積，該差異值越小，說明兩個頂點的結構特征越相似。

所述步驟3)中幾何信號的非局部均值濾波的具體實現為：

將步驟2)中定義的結構特征測度描述子作為非局部均值濾波權值的計算依據，對步驟1)中構造的幾何信號si進行非局部均值濾波得到一個新的幾何信號s′i，計算式為(8)式：

其中nσ(i)是頂點vi以σ為半徑的鄰域點集，σ為幾何模型平均邊長的β∈[1.5,3]倍，權重系數wij通過各頂點之間結構特征測度描述子進行計算，即為式(9)-(10)式：

h表示幾何模型去噪的強度，可取為h∈[0.05,0.35]。

所述步驟4)中幾何模型重建的具體實現為：

通過將濾波后新的信號s′i進行最小二乘求解得到新的幾何模型頂點v′，即最小化為(11)式表示的能量：

該能量可以改寫為(12)式：

其可以轉化為一個2n×n的線性方程組(13)式：

其中s′＝diag(s′1,s′2,…,s′n)表示以步驟3)中所得的頂點信號s′i作為對角線元素的矩陣，n為幾何模型頂點的個數，l為原始幾何模型的拉普拉斯矩陣，in×n為n階單位矩陣，n為原始幾何模型頂點的法向矩陣，v為原始幾何模型頂點的位置向量矩陣，μ為頂點約束的權重因子，邊界頂點的約束權值為1，內部頂點的約束權值為0.1。

本發明的優點體現在：

1.本發明提出的基于法向張量的結構特征描述子不僅考慮模型上單點的幾何量，還考慮整體特征方向的一致性，對有尖銳特征的cad模型和具有細節特征的非cad模型的特征均能較好的刻畫，具有較好的魯棒性；

2.本發明通過引入原始幾何模型頂點作為約束對于濾波后信號進行拉普拉斯模型重建，能夠在幾何模型平滑過程中阻止邊界和體積收縮；

3.本發明從幾何信號的角度出發，將非局部均值濾波引入到拉普拉斯幾何處理框架中，具有較高執行效率和很好的普適性。

附圖說明

圖1是本發明的一種基于結構特征描述的三維幾何模型去噪方法的流程圖；

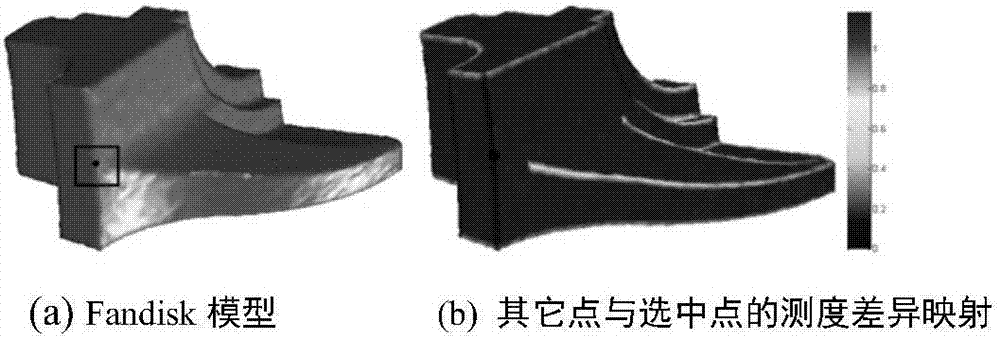
圖2是本發明具體實施中基于法向張量的結構特征測度描述的差異映射示意圖；

圖3是本發明具體實施中對幾何信號進行非局部均值濾波前后對比示意圖；

圖4為本發明具體實施中對octahedron模型的去噪結果示意圖；

圖5為本發明具體實施中對fandisk模型的去噪結果示意圖；

圖6為本發明具體實施中對mannequin模型的去噪結果示意圖；

圖7為本發明具體實施中對julius模型的去噪結果示意圖；

圖8為本發明具體實施中對angle模型的去噪結果示意圖；

圖9為本發明具體實施中對moai模型的去噪結果示意圖。

具體實施方式

下面利用附圖和實例對本發明作進一步說明。

參照圖1，本發明的一種基于結構特征描述的三維幾何模型去噪方法，包括以下步驟：

1)幾何信號的構建

讀入帶有噪聲的幾何模型，對具有尖銳特征的cad模型和具有細節特征的非cad模型均適用；對于以三角網格表示的三維幾何模型，通過幾何模型頂點的拉普拉斯算子和頂點法向進行內積構造幾何信號，該信號能夠刻畫幾何模型的局部細節特征；

所述步驟1)中幾何信號的構造的具體實現為：

設{vi|i＝1,2,…,n}為以三角網格表示的三維幾何模型的n個頂點，δ(vi)為頂點vi的離散拉普拉斯算子，頂點法向量為ni，將幾何信號定義為兩者內積形式為(1)式：

si＝(δ(vi),ni)(1)

對于幾何模型上所有頂點的幾何信號，可以寫成(2)式的矩陣形式：

lv＝sn(2)

其中v表示幾何模型頂點的位置向量矩陣，s＝diag(s1,s2,…,sn)表示以頂點信號si作為對角線元素的矩陣，n為頂點的法向矩陣，l為幾何模型的拉普拉斯矩陣，具有(3)式形式：

其中wij＝cotαij+cotβij，αij,βij是頂點vi與vj連線所成的邊所對的兩個角，n(i)是頂點vi的一環鄰域點集。

2)基于法向張量的結構特征描述子的計算

通過頂點法向張量的所有特征值的和以及最小單位特征向量作為結構特征測度描述子，該描述子能夠刻畫幾何模型上角點、邊點和面點的特征信息；

基于法向張量的結構特征描述子的計算具體實現為：

對于給定的幾何模型頂點vi，其法向張量可由它周圍的三角面片的單位法向量定義為(4)式：

其中f(vi)表示頂點vi周圍的三角形的指標集合，為(5)式的權重系數：

a(fk)是三角形fk的面積，amax是頂點vi周圍的三角形的最大面積，cfk是三角形fk重心，

由于法向張量為三階對稱半正定矩陣，可以求出其特征值λ1≥λ2≥λ3≥0和所對應的單位特征向量e1,e2,e3，由于幾何模型上角點、邊點和面點所對應的特征值有明顯的差距，而且最小特征向量的方向e3對應著頂點的特征方向，采用(6)式的度量作為頂點結構特征測度描述子：

des(vi)＝{di,ti}(6)

其中di＝λ1+λ2+λ3，ti對應頂點法向張量的最小特征向量；

在此基礎上，通過(7)式如下度量來計算各頂點之間結構特征描述子的差異：

d(vi,vj)＝(di-dj)²+(1-|(tj,ti)|)(7)

其中(tj,ti)表示頂點特征方向的內積，該差異值越小，說明兩個頂點的結構特征越相似。

圖2給出了在帶有噪聲的fandisk幾何模型的豎直方向的尖銳特征邊上選定一個頂點后，通過本發明提出的基于法向張量的結構特征測度描述方法對頂點進行描述時的差異映射示意圖。從中可以看到，豎直方向特征邊上的頂點與選定的頂點的相似性非常接近，說明該描述子能較好的描述具有相同結構特征的頂點的相似性，能夠有效地應用到非局部均值濾波的去噪框架中。

3)幾何信號的非局部均值濾波

通過各頂點相互之間結構特征測度描述子的差異作為非局部均值濾波的權值計算依據，對頂點的離散拉普拉斯算子與對應頂點法向量內積所得的幾何模型上信號進行非局部均值濾波，得到一個新的幾何信號；圖3給出了非局部均值濾波前后信號對比示意圖。

幾何信號的非局部均值濾波的具體實現為：

將步驟2)中定義的結構特征測度描述子作為非局部均值濾波權值的計算依據，對步驟1)中構建的幾何信號si進行非局部均值濾波得到一個新的幾何信號s′i，計算式為(8)式：

其中nσ(i)是頂點vi以σ為半徑的鄰域點集，σ為幾何模型平均邊長的β∈[1.5,3]倍，權重系數wij通過各頂點之間結構特征測度描述子進行計算，即為式(9)-(10)式：

h表示幾何模型去噪的強度，可取為h∈[0.05,0.35]。

4)幾何模型重建

將原始幾何模型頂點作為約束條件，通過將步驟3)所得的濾波后新的幾何信號進行拉普拉斯曲面重建，得到非局部均值濾波后信號對應的幾何模型。

幾何模型重建的具體實現為：

通過將濾波后新的信號s′i進行最小二乘求解得到新的幾何模型頂點v′，即最小化為(11)式表示的能量：

該能量可以改寫為(12)式：

其可以轉化為一個2n×n的線性方程組(13)式：

其中s′＝diag(s′1,s′2,…,s′n)表示以步驟3)中所得的頂點信號s′i作為對角線元素的矩陣，n為幾何模型頂點的個數，l為原始幾何模型的拉普拉斯矩陣，in×n為n階單位矩陣，n為原始幾何模型頂點的法向矩陣，v為原始幾何模型頂點的位置向量矩陣，μ為頂點約束的權重因子，邊界頂點的約束權值為1，內部頂點的約束權值為0.1。

圖4和圖5給出了針對具有尖銳特征的cad模型加入高斯噪聲后的去噪結果；圖6和圖7給出了對具有細節特征的非cad模型加入高斯噪聲后的去噪結果；圖8和圖9給出了含有真實噪聲的模型數據的去噪結果。

本發明的具體實施方式并非窮舉，本領域技術人員不經過創造性勞動的簡單復制和改進，應屬于本發明專利要求的保護范圍。