基于GPU+CPU異構平臺的三維大地電磁反演并行方法與流程
本發明涉及地質電磁勘探技術領域,尤其涉及一種基于gpu+cpu異構平臺的三維大地電磁反演并行方法。
背景技術:
大地電磁法(mt)作為一種實用的低成本(相對于地震勘探)地球物理勘探方法,在構造研究、石油勘探、礦產及水文勘探等領域扮演著重要角色,是探測巖石層電性結構的主要方法。大地電磁法的基本原理是:通過觀測天然變化的電磁場水平分量,經過數據處理計算阻抗和傾子張量數據,然后反演求得地下電阻率分布。在大地電磁法勘探數據的反演解釋中,主要的計算過程包括正演和反演,正演是指已知地下的電阻率分布,根據電磁理論計算地面上不同測點不同頻率的觀測數據的過程;反演是指根據觀測數據,求取地下的真實電阻率分布的過程,反演是一種最優化數學過程,其算法核心是求解當前猜測模型的正演,并對正演結果與實際觀測數據做誤差評價,求取修正量。
近年來,三維大地電磁法的正演、反演技術已實用化并取得了巨大進展。然而,隨著勘探數據集的增大、對于勘探精度的需求不斷提高,要求三維mt反演的計算速度更快、計算平臺成本更低廉。在現有技術中,主要采用兩種并行方案來提高計算速度。方案一、基于單機的多核cpu并行計算方案(如openmp),在反演的正演核中同時求解n個大型稀疏復線性方程組,n為計算機支持的最大并行線程數,例如,對于四核八線程cpu,可以同時執行8個線性方程組求解,因此,如果需要求解40個大型線性方程組,則需重復執行5次。該方案的缺點是由于單機只有一條系統總線,在同一時刻只有一個進程在執行,并行計算效率由cpu本身的緩存決定,一般加速比僅為cpu線程數的一半左右;方案二、適應并行計算集群(pc-cluster)的多節點并行計算方案(如openmpi),每個計算節點(等價于一臺單機)在需要做三維大地電磁反演的正演計算時會被分配任務,求解得到結果后再通過高速局域網匯總結果到主計算節點。該方案的缺點是并行機價格昂貴,并且需要專門的機房和維護人員,計算程序無法安裝在大地電磁數據采集的野外計算機上,而且針對并行機的mpi編程協議相對比較復雜,增加了開發成本,且代碼的調試和維護非常困難。
技術實現要素:
本發明的目的在于克服上述現有技術的缺陷,提供能夠充分利用單機硬件資源并提高三維大地電磁反演的并行計算能力的技術方案。
根據本發明的一方面,提供了一種基于gpu+cpu異構平臺的三維大地電磁反演并行方法,包括:
步驟1:基于網格剖分和單元電阻率值形成三維大地電磁的正演方程組;
步驟2:獲取求解所述正演方程組所需的存儲空間大小;
步驟3:基于所述存儲空間大小獲取gpu最大并行線程數ng和cpu最大并行線程數nc;
步驟4:將求解所述正演方程組的并行計算任務分配給空閑的gpu線程和cpu線程執行。
優選地,在步驟4中,計算任務的分配順序是,優先分配空閑的gpu線程,若gpu線程均不空閑則分配給cpu線程。
優選地,所述正演方程組表示為:
其中,xx、xy和xz為求解向量,bx、by和bz分別是各方向電場對應的右端項子向量,
優選地,以按行壓縮的稀疏矩陣方式將所述系數矩陣存儲為行指針數組、列下標數組和非零數值數組,所述列下標數組用于表示非零元素的列數,所述行指針數組用于表示該行的起始非零元素在列下標數組中的位置,所述非零數值數組表示所述系數矩陣中的非零元素。
優選地,使用一組公共行指針和列下標數組來存儲所有并行線程中的系數矩陣的所述行指針數組和所述列下標數組。
優選地,采用預條件穩定雙共軛梯度法求解每個并行線程的三維大地電磁正演方程組。
優選地,對于每個并行線程,需要的所述存儲空間包括臨時向量的內存需求、系數矩陣的內存需求和系數矩陣的預條件分解陣的內存需求。
優選地,所述系數矩陣的內存需求字節數為:ma=(n+1+nnz_a)*sizeof(int)+nnz_a*sizeof(double)*2,所述系數矩陣的預條件分解陣的內存需求字節數為:mp=(n+1+nnz_p)*sizeof(int)+nnz_p*sizeof(double)*2,所述臨時向量的內存需求字節數為:mv=9*n*sizeof(double)*2,其中,n表示系數矩陣的行數,nnz_a表示系數矩陣的非0元素個數,nnz_p表示預條件分解陣的非0元素個數,sizeof(int)表示整形變量需要的字節數,sizeof(double)表示雙精度浮點型變量需要的字節數。
優選地,所述gpu最大并行線程數為:ng=0.8*mg/m,ng表述gpu最大并行線程數,mg表示gpu支持的最大全局內存大小,m=ma+mp+mv表示gpu單線程所需的存儲空間大小。
與現有技術相比,本發明的優點在于:充分利用基于gpu+cpu的異構平臺的硬件資源,使用gpu參與三維大地電磁反演的并行計算;針對三維大地電磁方程組系數的特點,通過盡量壓縮內存需求的方式,提高gpu可支持的并行線程數,從而增加了gpu并行計算的適應場景。
附圖說明
以下附圖僅對本發明作示意性的說明和解釋,并不用于限定本發明的范圍,其中:
圖1示出了根據本發明實施例的基于gpu+cpu異構平臺的三維大地電磁反演并行方法的流程圖。
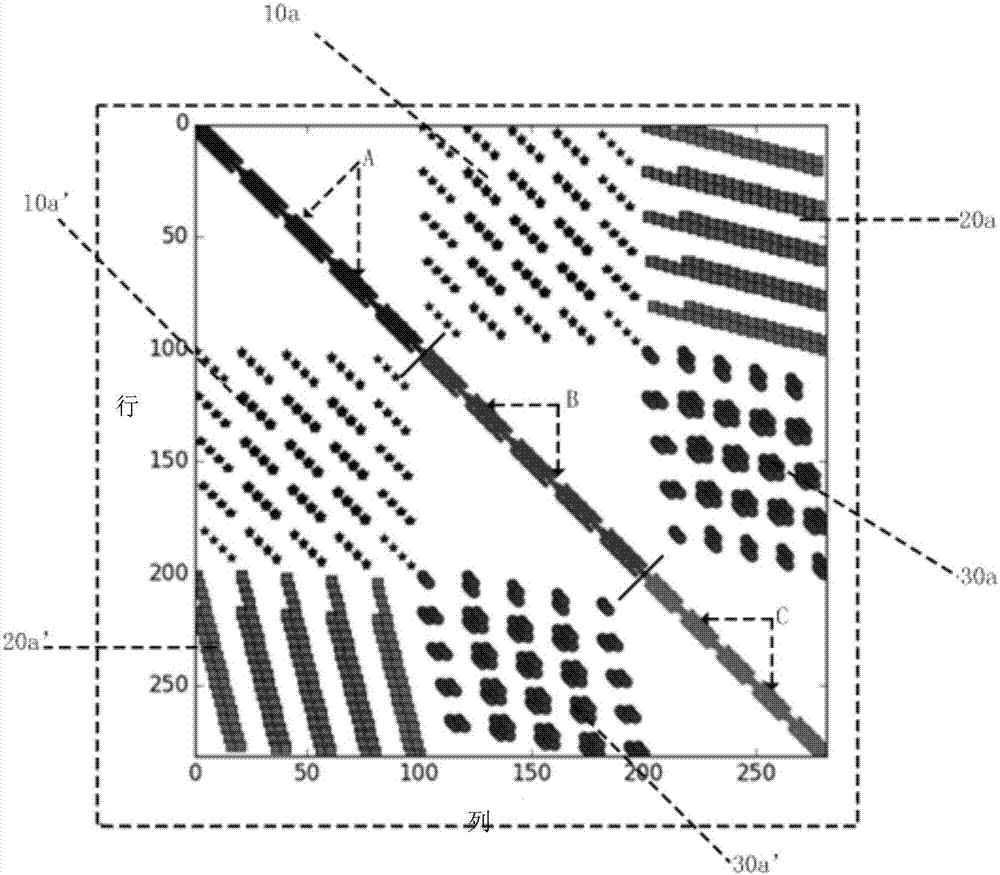
圖2示出了典型三維mt有限差分正演系數矩陣的稀疏模式示意圖。
圖3示出了稀疏矩陣csr三元組壓縮存儲格式示意圖。
具體實施方式
為了對本發明的技術特征、目的和效果有更加清楚的理解,現對本發明提出的基于gpu+cpu異構平臺的三維大地電磁反演并行方法作進一步說明。
本發明的并行計算方案實施步驟為:獲得三維大地電磁的正演矩陣方程組;獲取本機gpu支持的最大并行線程數ng;獲取cpu的最大并行線程數nc;在一組待分配的并行求解正演方程組的任務中,優先分配ng個gpu任務,并分配nc個cpu任務。
現參照圖1,結合本發明的一個實施例描述具體步驟,需要說明的是,說明書中描述的該方法的各個步驟并非一定是必須的,而是可以根據實際情形省略或替換其中的一個或多個步驟。
第一步:獲取正演矩陣方程組
首先,根據大地電磁反演的剖分和單元電阻率值形成初始正演矩陣方程組,典型地,初始正演矩陣方程組的形式為:
其中,ex、ey和ez分別表示求解向量的子向量,bx、by和bz分別是各方向電場對應的右端項子向量。axx、byy和czz分別為麥克斯韋方程電場二階旋度三分量展開的系數子矩陣,除主對角元素外,其它所有元素均和頻率及單元電導率無關。
在線性方程組(1)中,axy=byx、axz=czx、byz=czy,并且axx、byy和czz都是對稱子矩陣,可將其簡寫為:
其中,axx=axx,ayy=byy,azz=czz;axy=axy,axz=axz;ayz=byz,省略號表示對稱,xx=ex,xy=ey,xz=ez為求解向量。且axx、ayy和azz均為對稱子矩陣。
第二步:采用壓縮稀疏矩陣存儲形式表示初始矩陣。
方程組(2)是大量元素為零的稀疏系統,具有典型的稀疏模式,圖2示出了典型三維mt有限差分正演系數矩陣的稀疏結構(5×5×5,表示反演網格的x,y,z三個方向的網格剖分數目,也就是說網格有5*5*5=125個網格單元),其中,a、b、c像素點分別表示axx,ayy,azz,10a和10a’表示axy和ayx,20a和20a’表示axz和azx,30a和13a’表示ayz和azy。
在三維有限差分正演方程組中,系數矩陣每行最多有13個非零元素,為了節省內存空間和避免零元素的冗余運算,可考慮使用壓縮存儲方式。
在此實施例中,采用按行壓縮的csr(compressedsparserow)壓縮格式。csr是一種三元組壓縮方式,使用列下標(colinds)、行指針(rowptrs)和非零值(values)三個向量來存儲整個矩陣,其中,列下標colinds表示非零元素所位于的列數;行指針rowptrs表示該行從列下標中的哪個元素開始。行指針rowptrs中的最后一個元素是列下標中最后一個元素的編號,行指針rowptrs中的其他元素每個代表一行。如圖3所示,對于最右側的稀疏矩陣
例如,在一個實際應用的示例中,采用以下的c++代碼實現按行存儲的csr格式。
第三步:計算求解方程組所需的存儲空間。
方程組(2)的求解方法有多種,例如,krylov子空間迭代法等、以多波前(multifrontalmethod)技術為代表的直接法。在此實施例中,為了適應小內存場景,可采用krylov子空間迭代法中的預條件穩定雙共軛梯度法(bicgstab)。該方法的收斂速度與預條件陣p的選擇有關,每次迭代中近似快速求解pp=r,其中,p表示構建的預條件矩陣,p表示預條件系統的快速近似解,r表示預條件系統的右端項。
在本文中,使用公式(2)的系數矩陣的帶狀對稱部分來構建預條件,令:
為了便于理解,下面列出了bicgstab算法的偽代碼。在下述步驟中r0是初始殘差向量,b是右端項,a是系數矩陣,x0是初始解,
//bicgstab算法的偽代碼
step1:r0=b-ax0
step2:選擇任意向量
step3:設定系數:ρ0=α=ω0=1
step4:設定向量:v0=0,p0=0
step5:循環k=0,1,…:
5.1
5.2β=(ρk+1/ρk)(α/ωk)
5.3pk+1=rk+β·(pk-ωkvk)
5.4快速求解py=pk+1,vk+1=ay(y為中間向量)
5.5
5.6s=rk-αvk+1(s為中間向量)
5.7快速求解pz=s,t=az(z、t為中間向量)
5.8快速求解prk+1=t
5.9
5.10xk+1=xk+α·y+ωk+1z
5.11rk+1=s-ωk+1·t
5.12如果
//bicgstab算法的偽代碼
其中,p是稀疏對稱hermitian矩陣,快速求解pp=r需要對p進行不完全分解,在本發明中,可以采用不帶填充的不完全lu分解和不完全cholesky分解兩種方式,它們各有優點,使用不完全lu分解避免了根號操作,但需要存儲分解后的下三角和上三角兩個矩陣;不完全cholesky分解只需要存儲分解后的上三角(由于p對稱),但分解過程的根號操作可能導致數值計算錯誤。為了適應gpu的小內存場景,優選地,采用易于編程實現、內存需求最小、分解快的不完全cholesky分解法。
在上述bicgstab迭代流程中,輸入數據為按照csr壓縮存儲的稀疏系數矩陣a,預條件的不完全cholesky分解陣p,未知數向量x,右端項b。
在三維大地電磁有限差分正演中,假設x、y、z三個方向的單元格數目分別為nx、ny和nz,這三個方向的單元格數是反演之前由用戶設定的,一般和測點分布有關,則系數矩陣的行數n可以按如下的公式計算:
n=nx*(ny-1)*(nz-1)+(nx-1)*ny*(nz-1)+(nx-1)*(ny-1)*nz
預條件矩陣的不完全cholesky分解陣的非0元個數nnz_p為:
nnz_p=n+nx*(ny-1)*(nz-2)+nx*(ny-2)*(nz-1)+(nx-1)*ny*(nz-2)+(nx-2)*ny*(nz-1)+(nx-2)*(ny-1)*nz+(nx-1)*(ny-2)*nz。
系數矩陣的非0元個數nnz_a為:
nnz_a=nnz_p+8*(nx-1)*(ny-1)*(nz-1)+4*(nx-1)*(ny-1)*(nz-1)。
綜上所述,只要通過三個方向的單元個數nx、ny、nz即可求得系數矩陣的行數n、預條件矩陣的分解陣的非0元個數nnz_p、以及系數矩陣的非0元個數nnz_a。
在一個gpu線程中在gpu上開辟的內存空間包括稀疏矩陣需要的存儲空間和計算過程中向量所需的存儲空間。在此實施例的bicgstab算法中,x、b、r、r_tld、p、p_hat、s、s_hat、v、h這10個向量中b向量和r向量在算法中可以合并,因此向量內存需求的字節數為mv=9*n*sizeof(double)*2。
其中,所有向量和矩陣的參數均是雙精度復數類型,雙精度復數類型在c/c++語言系統下的字節數為sizeof(double)*2,即實部和虛部均為double型;9是求解方程的算法中涉及到合并之后的向量個數。
而稀疏矩陣的內存需求分兩個部分,整形的下標數組和非0元素數組的大小,系數矩陣a的內存需求字節數ma為:
ma=(n+1+nnz_a)*sizeof(int)+nnz_a*sizeof(double)*2
預條件矩陣的分解陣的內存需求字節數mp為:
mp=(n+1+nnz_p)*sizeof(int)+nnz_p*sizeof(double)*2
從而單一gpu線程的一個頻率的三維大地電磁有限差分正演的bicgstab迭代求解的總內存需求包括計算向量的內存需求、系數矩陣的內存需求和預條件矩陣的分解陣的內存需求三者之和,即單線程的總內存需求m=mv+ma+mp個字節。
本領域的技術人員應當理解,盡管上述以預條件穩定雙共軛梯度法(bicgstab)為例,介紹了計算求解方程組的所需存儲空間的方法,但是也可以利用本發明的原理采用其它的算法或矩陣分解方法來獲得存儲空間的大小。
第四步:分配gpu并行線程數和cpu的并行線程數。
為了實現并行計算,在此步驟中需要分配執行方程組求解的gpu并行線程數和cpu的并行線程數。
根據本發明的一個實施例,獲得gpu線程數的方法是,對于nvidia公司的顯卡gpu設備,其提供的cuda并行計算庫提供了底層的api函數獲取gpu設備的內存情況。假定計算機有兩個gpu顯卡,首先使用cudagetdevicecount(&ngpu)函數即可得到當前支持cuda并行的gpu設備個數為2,編號分別為0和1。本發明的計算方案在分配任務時優先分配gpu線程,所以在一個外部openmpi循環中,首先會查看0號gpu的情況,然后是1號gpu,以此類推。也可以首先分配gpu1的線程,本發明對gpu之間的并行線程分配順序不作限制。
以0號gpu為例,首先,需要調用cudagetdeviceproperties(&prop,0)來獲取0號gpu的屬性prop,prop是一個cuda屬性結構體,0號gpu支持的最大全局內存數目mg為prop.totalglobalmem,從而0號gpu的最大線程數ng0=0.8*mg/m(為了不超過顯存空間,可向下取整),其中m為之前獲得的單線程所需的總存儲空間,這種分配方式給gpu留下了20%的空余空間,以用于cuda計算庫的高級向量操作函數的擴展內存需求。在其他實施例中,也可以根據其他操作對內存的需求情況,預留多于或少于20%的空余空間。
根據本發明的一個實施例,獲得cpu最大線程數nc的方法是,可以使用openmp協議的nc=omp_get_max_threads()函數,在默認情況下得到當前多核計算機的并行虛擬內存數,cpu線程數若大于這個數目則加速比會下降。該函數為openmp標準函數,其得到的是計算機能支持并行的最大虛擬線程數,nc表示在沒有gpu設備的情況下,只用cpu進行密集型計算的最佳并行線程數。在cpu+gpu異構計算機上,由于gpu線程的密集計算在顯卡上執行,還可以在nc個密集計算線程的基礎上,增加ng個線程用于gpu并行計算的數據拷貝等空閑時間較多的線程,這ng個線程即gpu線程。
因此,基于本發明的方法,一個外部openmp循環需要分配nc個cpu線程和ng0+ng1+…個gpu線程,假設50*50*50的大地電磁問題,在單4g顯存gpu、4核8線程計算機上,同時參與計算的線程數目為8個低速cpu線程和2個高速gpu線程。
上述分配方式中,存在的一個問題是,在求解問題規模太大的情況下,如果gpu顯存不夠,此時gpu的1個線程在求解方程時會反復的釋放、申請、拷貝內存,從而降低gpu顯存的計算速度,有可能整體加速比還不如純cpu并行。因此,在一個實施例中,若mg*80%<m,則完全禁止gpu,僅分配用cpu來做并行計算。但應說明的是,對于大規模計算問題,并行的最佳方案是高成本的并行計算機集群而不是單機。
應理解的是,基于本發明的方法,在分配任務時,一次并行總任務數為ng+nc個,由于每個任務不是同時執行完畢的,假設某時刻已經空出了一個計算資源,此時需要給其分配新的計算任務,此新任務應優先分配給gpu,如果ng個gpu都不空閑,則分配給cpu,整個并行計算中,所有gpu和cpu計算資源均是無空閑的滿負荷運作,它們所有的線程均是同時執行的。
上述根據圖1的實施例重點描述了分配gpu和cpu線程數的方法以及系數矩陣的壓縮存儲方式。然而,對于基于gpu和cpu的異構并行計算而言,由于gpu內存有限,目前市場上最大的只有8g,一個大型大地電磁反演網格的串行求解線程可能需要4g左右的內存,需要進一步考慮大型復線性方程組的壓縮存儲問題。
在一個實施例中,基于大地電磁的不同的求解線程矩陣雖然不同,但稀疏規律一樣,使用一組行、列向量來表示所有矩陣的稀疏模式。例如,若有40個頻率的大地電磁數據,系數矩陣有40個,每個矩陣的稀疏壓縮存儲需要rowptrs,colinds,vals三個數組表示,傳統方式需要存40個這樣的三個數組。而在本發明中,為了進一步降低內存需求,考慮到rowptrs,colinds這兩個數組(大型致密)對于40個頻率都是一樣的,因此,只需存儲一組rowptrs,colinds行列指針向量,和40個vals矩陣的非0元素向量,通過這種方式可以節省39*2個大型致密數組的存儲空間。
具體如下:
若一個線性方程組的偽代碼示意性表示為:
在傳統方式的多個線程中,所有的稀疏矩陣在并行計算時內存表示為:
為了避免稀疏屬性的行指針和列向量在同一并行架構內存中的重復內容,在本發明中,采用的新表示法為:
因此,通過這種方式,一方面壓縮了內存,另一方面減少了gpu并行計算中的內存拷貝操作。對于每個計算線程而言,系數矩陣a和預條件分解矩陣p的下標向量都是一樣的,如果每個線程都要申請單獨的下標向量就會浪費了不少內存。例如,假定現在有40個頻率,矩陣的規模為n行,a和p矩陣的非0元素為nnz_a和nnz_p個,那么完全可以用1下標數組結構體代替另外需要分配的40個,需要的下標結構體為4個整型數組,rowptra、colinda、rowptrp、colindp,一個gpu線程需要的顯存大小ms為:
ms=(n+n+nnz_a+nnz_p)*sizeof(int)
而采用公用的下標結構體節省了39*ms的內存需求(假定40個線程同時并行),對于網格規模為100*100*100的問題來說,至少節省了4g的內存空間的申請、釋放和拷貝工作,提速將非常明顯。
總之,相對于現有技術,本發明的方案能夠在現有的主流高配計算機上接近并行機的三維大地電磁反演計算速度,能夠有效的提高計算速度并降低成本。
例如,以三維大地電磁反演的典型問題規模為例,假設需要反演40個頻率、網格規模為50*50*50的數據,此時一個正演問題需要求解80個大型線性方程組,單核計算每個方程組時間為一個單位時間,內存需求為1g。假定計算機為4核8線程,gpu顯存8g。計算機價格大約10000元左右。純單機cpu并行(現有技術方案一)的加速比大致為4,那么一次正演需要20個單位時間。在不考慮數據網絡傳輸成本的情況下,10個4核8線程節點并行機的一次正演需要2個單位時間。但并行計算機+機房+維護人員成本估計100萬元左右。
而采用本發明的方法,gpu上可以并行執行8個線程,加速比最保守的估計為16(gpu線性代數庫最低比串行快兩倍),總體加速比為20,執行一次正演需要4個單位時間。不增加任何成本。
本發明可以是系統、方法和/或計算機程序產品。計算機程序產品可以包括計算機可讀存儲介質,其上載有用于使處理器實現本發明的各個方面的計算機可讀程序指令。
計算機可讀存儲介質可以是保持和存儲由指令執行設備使用的指令的有形設備。計算機可讀存儲介質例如可以包括但不限于電存儲設備、磁存儲設備、光存儲設備、電磁存儲設備、半導體存儲設備或者上述的任意合適的組合。計算機可讀存儲介質的更具體的例子(非窮舉的列表)包括:便攜式計算機盤、硬盤、隨機存取存儲器(ram)、只讀存儲器(rom)、可擦式可編程只讀存儲器(eprom或閃存)、靜態隨機存取存儲器(sram)、便攜式壓縮盤只讀存儲器(cd-rom)、數字多功能盤(dvd)、記憶棒、軟盤、機械編碼設備、例如其上存儲有指令的打孔卡或凹槽內凸起結構、以及上述的任意合適的組合。
以上已經描述了本發明的各實施例,上述說明是示例性的,并非窮盡性的,并且也不限于所披露的各實施例。在不偏離所說明的各實施例的范圍和精神的情況下,對于本技術領域的普通技術人員來說許多修改和變更都是顯而易見的。本文中所用術語的選擇,旨在最好地解釋各實施例的原理、實際應用或對市場中的技術改進,或者使本技術領域的其它普通技術人員能理解本文披露的各實施例。
- 還沒有人留言評論。精彩留言會獲得點贊!