一種基于動態時序圖的不確定性機車仿真模型系統構建方法與流程

本發明涉及機車控制方法，尤其涉及一種基于動態時序圖的不確定性機車仿真模型系統構建方法。

背景技術：

列車運行控制是一個典型的多目標、多約束、非線性的復雜實時變化過程。因此列車操縱問題是一個非線性有約束動態最優化問題。而列車在實際運行控制過程中，需要考慮列車安全限速、牽引電機飽和特性和車間最大耦合力等約束條件，同時還需綜合考慮運營準時性、節能高效和乘客乘坐舒適度等性能指標。為了保證鐵路的安全行駛和提高運輸的效率，許多國家和大經濟體都在積極的展開高速鐵路方面的研究。而出于安全、高效、方便等方面的考慮，設計出針對列車的運行過程仿真系統是很有必有的。

所謂系統仿真，是在系統分析的基礎上，對系統的各個部分的性質包括它們之間的關系的性質進行分析，從而創建出能夠對系統結構和系統的運行狀態、過程進行描述，并且擁有符合要求的數量和邏輯的關系的仿真模型，同時進行試驗，并且需要根據實驗的結果進行定性或者定量的研究，來對系統進行正確的判斷。在一般情況下，仿真系統都是利用客觀的系統模型，代替真實模型進行客觀的、真實的實驗，并在這實驗的基礎上，進行系統性能等方面的評價。

railsys是由德國漢諾威大學(universityofhannover)和德國鐵路管理咨詢公司(rmcon)共同進行開發研究的鐵路運行模擬仿真系統。它作為一款對鐵路的運行時間表和鐵路的基礎設施進行優化管理的仿真軟件，能夠進行鐵路交通網絡的建立分析、設計優化。甚至可以對列車對某一條線路的占用和當前可用的鐵路情況進行綜合的分析，還可以對信號的安全性，列車的運行進行評鑒。可以全面的呈現鐵路網絡系統的實際運行情況，對分析鐵路無時不刻在變化的運輸量對固定的鐵路運行能力的影響、鐵路中的相關設施是否需要新建、信號系統的安全及可用性評價、列車時刻表的制定和優化等起到重要的輔助決策作用。該系統目前在歐洲和世界鐵路運輸行業得到了廣泛的應用，如悉尼，科隆.萊茵.堪培拉的高速鐵路線，慕尼黑、科隆、悉尼、墨爾本的城市鐵路以及柏林和哥本哈根的鐵路網絡等。

隨著計算機技術的快速發展，國內很多學者也進行了相關研究，如郜春海，唐濤等做的“高速鐵路列車運行控制系統車載設備的軟件設計”，主要進行了高速鐵路列車運行控制系統車載設備功能軟件的設計；茍徑，寧濱等做的“列車追蹤運行仿真系統的研究與實現”，

唐金金，周磊山做的“高速列車運行仿真系統研究"，彭其淵，石紅國等做的“城市軌道交通列車牽引計算”。同時在列車仿真系統的建立和實現上，也有比較全面的進步。如盧衍丹在“鐵路信號與列車控制系統的面向對象仿真”中提出了基于模型庫的ato仿真系統，主要是將ato系統分解成為一些有獨立屬性和操作的獨立的單元，并提出建立了一種新的列車模型庫的建立方法，這樣深化了列車模型庫的建立；如張勇，張維維做的“ctcs.3級列控系統車載設備仿真測試平臺研究”方面的研究都是關于列車仿真軟件方面的應用。

而目前傳統的機車預測控制模型存在以下問題：(1)能仿真模擬的機車運行情景是有限的，不能完全滿足實際自動駕駛需求(2)在設計列車各車廂分布式牽引力和制動力時，可能會造成拖車在牽引到巡航的轉換階段有制動力輸出的情況，增大了列車運行能耗；(3)有些方案需要實時在線求解優化問題，會造成控制器設計過程計算量大、硬件實現成本高等問題，極大地限制了其應用范圍和應用場合。

因此，在處理機車駕駛仿真時，好的機車運行環境模型對后期使用機器學習等人工智能方法進行優化駕駛研究至關重要。機車自動駕駛是個算法模型與環境不斷交互學習的過程，所以算法訓練環境是自動駕駛算法得以實現的重要因素。而機車運行環境中包含了眾多不確定性因素(如天氣變化等)，所以亟待構建不確定性的機車運行環境模型實現對外界環境的有效模擬方法。

技術實現要素：

本發明的目的在于

本發明的技術方案是一種基于動態時序圖的不確定性機車仿真模型系統構建方法，其特征在于：

步驟1、利用基本動力學模型構建基礎環境模型

該步驟中，基于機車運行日志，通過監督式的學習算法來完成機車基礎環境模型的學習與構建；其中：

基礎環境模型的輸入為具體機車運行環境參數，包括車重、車長、速度、天氣、重力加速度、空氣阻力、轉動阻力、曲度；

基礎環境模型可用如下公式表示：

其中，m為機車質量；t為時間；ρ為機車旋轉質量的計數因子；v為機車速度；s為機車位移；

f(s)為當前位置的牽引力或者制動力；

rb(v)為機車基本阻力；

rl(s)為軌道阻力；

步驟2、注入動態時序圖模型,動態時序圖模型為一個基于隱馬爾科夫模型的狀態轉移圖模型；

步驟3、完成動態時序圖模型的不確定性參數學習，即隱馬爾可夫模型的學習與訓練；

步驟4、動態時序圖學習完畢后，輸入具體不確定環境因素，不確定環境因素包括大雨天氣、出現輪滑，將不確定環境因素作為模型的觀察序列，即可模擬產生隱藏狀態序列，及確定如何對基本物理模型修改參數使其能適應該具體環境因素下的機車運行。

進一步地，步驟3中，隱馬爾可夫模型的學習和訓練過程就是得到狀態轉移矩陣，混淆矩陣，以及初始化概率向量，具體包括：

(1)首先對于隱馬爾科夫模型的參數進行一個初始的估計，然后通過對于給定的數據評估參數的的價值并減少它們所引起的錯誤來重新修訂參數；

(2)根據需要建立模型的隱形狀態數，首先給定初始參數λ0＝(π，a,b)，在構建不確定性機車運行環境時，具體給定的初始參數如下：

π:初始概率向量；

a：狀態轉移矩陣；

b：混淆矩陣；

(3)利用baum-welch重估公式進行參數估計，直到達到收斂誤差或最大迭代步長；

(4)迭代后更新的三元組(π,a,b)，便得到構建不確定性機車運行環境問題的新馬爾科夫模型

本發明的有益效果在于：

本發明的優點在于：基于動態時序圖模型，進行列車運行環境擾動參數的學習。動態時序圖模型適應于狀態圖隨時間動態改變的應用場景，能夠提供較為精準的預測結果。應用該模型進行列車運行環境擾動參數的學習，與基礎模型參數學習共同構建成完善的列車運行環境模型，從而更能適應多變的機車運行環境仿真模擬。

附圖說明

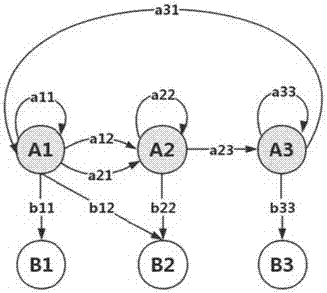
圖1是一組用于識別和預測的時間序列；

圖2是流程圖；

具體實施方式

下面結合附圖1-2對本發明的具體技術方案進行詳細描述。

該實施例提供了一種基于動態時序圖的不確定性機車仿真模型系統構建方法。該方法主要包括以下步驟；首先進行基礎環境模型的學習與構建，其次設計動態時序圖模型以適用于機車運行場景，然后進行動態時序圖模型的學習與構建，最后輸入具體的不確定環境因素，利用構建好的模型獲得適應于該情形的機車運行模型，更具體地包括：

步驟1、利用基本動力學模型構建基礎環境模型

通常，模型的構建分為基礎環境模型構建和不確定性環境參數變化趨勢學習兩個部分。由于機車的運行遵循基本動力學模型，該實施例中，擬基于機車運行日志，通過監督式的學習算法來完成機車基礎環境模型的學習與構建。

基礎環境模型指該模型的輸入為具體機車運行環境參數，包括車重、車長、速度、天氣、重力加速度、空氣阻力、轉動阻力、曲度，具體機車運行環境參數均可以從機車運行日志中獲取。

基礎環境模型可用如下公式表示：

其中，m為機車質量；t為時間；ρ為機車旋轉質量的計數因子；v為機車速度；s為機車位移；

f(s)為當前位置的牽引力或者制動力；

rb(v)為機車基本阻力，包含轉動阻力和空氣阻力，其經驗公式可定義為：

rb(v)＝m(a1+a2v+a3v²)

其中a1,a2,a3均為經驗常數系數。

rl(s)為軌道阻力，軌道阻力是由軌道坡度、曲度、隧道等因素產生的，軌道阻力可由如下公式給出定義：

rl(s)＝m*g*sinα(s)+fc(r(s))+ft(lt(s),v)

其中，g為重力加速度，α(s)、r(s)、lt(s)分別表示坡度、彎道半徑，以及隧道長度。其中彎道阻力fc()和隧道阻力ft()可以由以下公式定義：

當機車在隧道中行駛時，會受到更大的空氣阻力，這取決于隧道形狀，隧道墻面的粗糙程度，以及機車外觀設計等等因素。

步驟2、注入動態時序圖模型,動態時序圖模型為一個基于隱馬爾科夫模型的狀態轉移圖模型。

該實施例中，利用動態時序圖進行不確定性機車仿真的方法可以將實際運行環境中存在的眾多非確定性擾動因素考慮進來，具體實現方法可以有多種,比如可以采用改進的隱馬爾科夫回歸模型和baum-welch回歸算法相結合的動態時序圖方法來實現對不確定性環境參數變化趨勢的學習，從而完善機車運行環境模型。包含不確定性的機車運行環境模型的成功構建將為機車自動駕駛算法的訓練與驗證提供有效的支持。

在實際機車運行環境中，環境參數可能會產生不確定性擾動，此時學習到的基礎環境模型將無法覆蓋該場景。針對此問題，本發明基于動態時序圖模型，進行列車運行環境擾動參數的學習。

基于隱馬爾科夫模型的狀態轉移圖模型能夠適應于狀態圖隨時間動態改變的應用場景，能夠提供較為精準的預測結果。應用該模型進行列車運行環境擾動參數的學習，與基礎模型參數學習共同構建成完善的列車運行環境模型。

一個隱馬爾科夫模型應包含兩層：隱藏層和可觀測層。

隱藏層由馬爾科夫鏈構成，可以看做有限狀態機，每個狀態si都帶有狀態轉移概率。

可觀測層是一組用于識別和預測的時間序列ci。如圖1所示：

一個隱馬爾科夫模型是一個三元組，即：

初始化概率向量：π＝(πi),其中πi＝p(i1＝qi),i＝1,2,…,n

狀態轉移矩陣：a＝(aij),其中

混淆矩陣：b＝(bij),其中bij＝p(bi|aj)

該實施例中，不確定性機車仿真模型可以使用hmm來進行描述，我們可以根據一個觀察序列(來自于已知的集合)，以及與其有關的一個隱藏狀態集，估計一個最合適的隱馬爾科夫模型(hmm)，也就是確定對已知序列描述的最合適的(π,a,b)三元組。

在該模型中，隱藏狀態為列車運行環境擾動參數的改變情況，即基礎模型中出現的機車基本阻力系數a,b,c、彎道阻力系數fc和隧道阻力系數ft。

而觀察狀態為實際中我們可以觀察到的機車運行狀態，即正常運行、空轉、輪滑、超速等等。具體隱藏狀態、觀察狀態的設計體現在如下狀態轉移矩陣和混淆矩陣中。然后通過實際的機車運行日志得到一些列觀察狀態序列完成hmm模型的學習。

模型狀態轉移矩陣

模型混淆矩陣

步驟3、完成動態時序圖模型的不確定性參數學習，即隱馬爾可夫模型的學習與訓練

學習隱馬爾可夫模型的過程實則為得到其狀態轉移概率矩陣，混淆矩陣，以及初始概率向的混淆矩陣。然而，在許多實際問題的情況下這些參數都不能直接計算的，因此我們首先需要進行估計。

進行參數估計的方法有很多種，以baum-welch算法為例，baum-welch算法就可以以一個觀察序列為基礎來進行這樣的估計，而這個觀察序列來自于一個給定的集合，它所代表的是一個隱馬爾科夫模型中的一個已知的隱藏集合。具體來講，需要以下步驟：

(1)首先對于隱馬爾科夫模型的參數進行一個初始的估計，然后通過對于給定的數據評估這些參數的的價值并減少它們所引起的錯誤來重新修訂這些hmm參數。

(2)根據需要建立的模型的隱形狀態數，首先給定初始參數λ0＝(π，a,b)，在構建不確定性機車運行環境時，具體給定的初始參數可以設計如下：

π:初始概率向量，即時刻t＝1時，處于各隱藏狀態，即ai：如增大基本阻力系數a/b/c、減小彎道阻力系數ft、保持系數不變的概率；

a：狀態轉移概率矩陣。如在t時刻處于增大基本阻力系數a的狀態下，在t+1時刻處于減小彎道阻力系數ft的狀態下的概率。

b：混淆矩陣，如處于減小彎道阻力系數ft狀態下時，機車發生輪滑現象的概率。

步驟(1)和步驟(2)便是模型學習的輸入參數，這些輸入僅僅通過先驗知識輸入即可，即便是錯誤的也沒關系，后期模型學習過程中會自動更正。

(3)利用baum-welch重估公式進行參數估計，直到達到收斂誤差或最大迭代步長。

(4)迭代后更新的三元組(π,a,b)便是適用于構建不確定性機車運行環境問題的新馬爾科夫模型。

步驟4、動態時序圖學習完畢后，輸入具體不確定環境因素，不確定環境因素包括大雨天氣、出現輪滑，將不確定環境因素作為模型的觀察序列，即可模擬產生隱藏狀態序列，及確定如何對基本物理模型修改參數使其能適應該具體環境因素下的機車運行。

而根據模型的觀測序列推出最有可能的隱藏狀態序列的算法有很多，比如viterbi算法。

盡管以上結合附圖對本發明的實施方案進行了描述，但是本發明并不同限于上述的具體實施方案和應用領域，上述的具體實施方案僅僅是示意性的、指導性的，而不是限制性的。本領域的普通技術人員在說明書的啟示下，在不脫離本發明權利要求所保護的范圍的情況下，還可以做出很多種的形式，這些均屬于本發明保護之列。