基于徑向基函數神經網絡模型的測井曲線預測方法與流程
本發明涉及油氣井的測井曲線數據采集方法,尤其是一種快速有效、幾乎無成本和預測測井曲線準確的基于徑向基函數神經網絡模型的測井曲線預測方法。
背景技術:
隨著油氣開采技術的不斷進步,測井曲線數據采集一般都是在鉆井過程中采用專業設備測量獲得,以便后期對油氣田所處區域地質結構、油氣儲層以及油氣開采研究提供基礎數據。所述的測井曲線數據一般包括聲波曲線ac、自然伽馬曲線gr、中子曲線cnl、電阻率曲線rt、井徑曲線cal等相關曲線,這些曲線都是在鉆井過程中采用專業測井設備測量獲得。然而,一個油氣田所處區域油氣開采是一個連續性的事件,從勘探至開采最短時間基本都需要幾十年,在對油氣進行開采過程中,以前的老井,沒有獲取收集測井曲線數據,或者由于技術條件限制,獲取收集的測井曲線數據不全,這對后期研究而言是相當困難,缺失的測井曲線數據是無法重新測量的。因為以前的老井在鉆井過程中,都基本采用三層套管,套管之間采用砼澆筑,在鉆井過程中不采集測井曲線數據,后期是無法采集的;以前的老井在鉆井時,測井曲線檢測儀器還沒有發明制造出來【例如聲波曲線ac的檢測儀】,也無法完整的采集測井曲線。
基于上述情況,老井的測井曲線預測方法就變得很有必要,以實現對老井的測井曲線采集。
技術實現要素:
本發明的目的是提供一種快速有效、幾乎無成本和預測測井曲線準確的基于徑向基函數神經網絡模型的測井曲線預測方法。
為實現上述目的而采用的技術方案是這樣的,即一種基于徑向基函數神經網絡模型的測井曲線預測方法,其特征在于:包含所要預測的老井和與老井所處同一油氣田的至少一口新井,已知新井的多條測井曲線,運用人工神經網絡技術建立預測模型,然后利用該預測模型和已知新井的測井曲線對缺失測井曲線的老井進行測井曲線預測。運用人工神經網絡技術建立預測模型的步驟如下,
第一步、選定標準井,
所述標準井為測井曲線較全的新井,該新井的測井曲線為常規測井曲線,該常規測井曲線是指聲波曲線ac、自然伽馬曲線gr、中子曲線cnl、電阻率曲線rt、井徑曲線cal等具體測井曲線;
第二步、確定老井需要預測的具體測井曲線,
假定老井需要預測的某一具體測井曲線為輸出且用y表示,老井需要預測的其它具體測井曲線也為輸出,其它具體測井曲線的個數為p個,其它具體測井曲線也為輸出對應用x1、x2、…、xp表示,其中p為≧2的自然數;
假定用于建立預測模型的具體測井曲線有n個取樣點,對應的用向量x1、x2、…、xn表示輸入,其中n為>1的自然數,其中第k個輸入為xk=[x1k、x2k、…、xpk]t,k=1,2,…,n,所對應的n個輸出用向量y=[y1、y2、…、yn]t表示;t表示轉置,寫成行向量,轉置就是列向量;
第三步、構建輸入—輸出訓練樣本集,從上述第二步所述n個樣本中選擇m個樣本構成基函數的中心,這里采用的是自組織選取中心法,中心位置是動態變化的,然后將n個樣本反復輸入,直到中心位置穩定為止。
xj=[x1j、x2j、…、xpj]t,j=1,2,…,m,
所述m為>1的自然數,
選擇m個基函數,每個基函數對應一個訓練數據,各基函數的形式為
訓練數據點xj是基函數
第四步、建立預測模型,
基于第三步所述徑向基函數的人工神經網絡模型為
式中j為模式號、m為訓練模式總數、p為度量空間的維數、x為要預測的某個點的參數(輸入);y是對應的輸出。
將第n個訓練樣本xi,yi分別帶入上述模型學習訓練,得到
上式實際上是一個關于m個未知數(權值系數)ωj(j=1,2,…,m)的線性方程組,令
基函數采用reflectedsigmoidal(反演s型)函數
其中
由于n>m,所以上述方程組是一個超定方程組,解此方程組可獲得m個未知數(權值系數)ωj(j=1、2、…、m)的解,于是便可得到基于自組織選擇中心法的徑向基函數人工神經網絡預測模型為
式中x表示輸入,y表示輸出,xj(j=1、2、…、m)表示m個訓練中心;
第五步、預測老井所需要預測的測井曲線,
將老井所要預測井段的測井曲線(取樣點)值xi=[x1i、x2i、…、xpi]t依次帶入
本發明所述方法的優點是:快速、有效而且幾乎無成本的得到老井的缺失的測井曲線。
附圖說明
本發明可以通過附圖給出的非限定性實施例進一步說明。
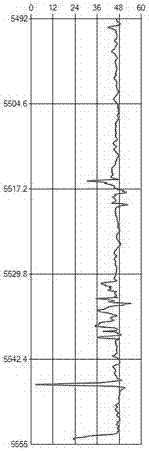
圖1為本發明的新井實測的聲波曲線和預測的聲波曲線示意圖。
圖2為本發明的老井預測的聲波曲線示意圖。
具體實施方式
下面結合附圖和實施例對本發明作進一步說明:
基于徑向基函數神經網絡模型的測井曲線預測方法,其特征在于:包含所要預測的老井和與老井所處同一油氣田的至少一口新井,已知新井的多條測井曲線,運用人工神經網絡技術建立預測模型,然后利用該預測模型和已知新井的測井曲線對缺失測井曲線的老井進行測井曲線預測。運用人工神經網絡技術建立預測模型的步驟如下,
第一步、選定標準井,
所述標準井為測井曲線較全的新井,該新井的測井曲線為常規測井曲線,該常規測井曲線是指聲波曲線ac、自然伽馬曲線gr、中子曲線cnl、電阻率曲線rt、井徑曲線cal等具體測井曲線;
第二步、確定老井需要預測的具體測井曲線,
假定老井需要預測的某一具體測井曲線為輸出且用y表示,老井需要預測的其它具體測井曲線也為輸出,其它具體測井曲線的個數為p個,其它具體測井曲線也為輸出對應用x1、x2、…、xp表示,其中p為≧2的自然數;
假定用于建立預測模型的具體測井曲線有n個取樣點,對應的用向量x1、x2、…、xn表示輸入,其中n為>1的自然數,其中第k個輸入為xk=[x1k、x2k、…、xpk]t,k=1,2,…,n,所對應的n個輸出用向量y=[y1、y2、…、yn]t表示;t表示轉置,寫成行向量,轉置就是列向量;
第三步、構建輸入—輸出訓練樣本集,從上述第二步所述n個樣本中選擇m個樣本構成基函數的中心,這里采用的是自組織選取中心法,中心位置是動態變化的,然后將n個樣本反復輸入,直到中心位置穩定為止。
xj=[x1j、x2j、…、xpj]t,j=1,2,…,m,
所述m為>1的自然數,
選擇m個基函數,每個基函數對應一個訓練數據,各基函數的形式為
訓練數據點xj是基函數
第四步、建立預測模型,
基于第三步所述徑向基函數的人工神經網絡模型為
式中j為模式號、m為訓練模式總數、p為度量空間的維數、x為要預測的某個點的參數(輸入);y是對應的輸出。
將第n個訓練樣本xi,yi分別帶入上述模型學習訓練,得到
上式實際上是一個關于m個未知數(權值系數)ωj(j=1,2,…,m)的線性方程組,令
基函數采用reflectedsigmoidal(反演s型)函數
其中
由于n>m,所以上述方程組是一個超定方程組,解此方程組可獲得m個未知數(權值系數)ωj(j=1、2、…、m)的解,于是便可得到基于自組織選擇中心法的徑向基函數人工神經網絡預測模型為
式中x表示輸入,y表示輸出,xj(j=1、2、…、m)表示m個訓練中心;
第五步、預測老井所需要預測的測井曲線,
將老井所要預測井段的測井曲線(取樣點)值xi=[x1i、x2i、…、xpi]t依次帶入
在該方法中,快速、有效而且幾乎無成本的得到老井的缺失的測井曲線,有了老井完整的測井曲線,可以充分利用老井的測井曲線對研究區域進行較為客觀的地質認識。預測老井缺失的測井曲線準確度高,所預測老井缺失的測井曲線與老井附近新開的新井測量得到的測井曲線比較,誤差很小。
參見附圖1和2,圖中以人工神經網絡預測模型
顯然,上述所有實施例是本發明的一部分實施例,而不是全部的實施例。基于本發明所述實施例,本領域技術人員在沒有做出創造性勞動前提下所獲得的所有其它實施例,都屬于本發明保護的范疇。
綜上所述,由于上述方法,本發明快速、有效而且幾乎無成本的得到老井的缺失的測井曲線。
- 還沒有人留言評論。精彩留言會獲得點贊!