一種地震力作用下節理巖質邊坡傾倒破壞極限承載力分析下限法的制作方法

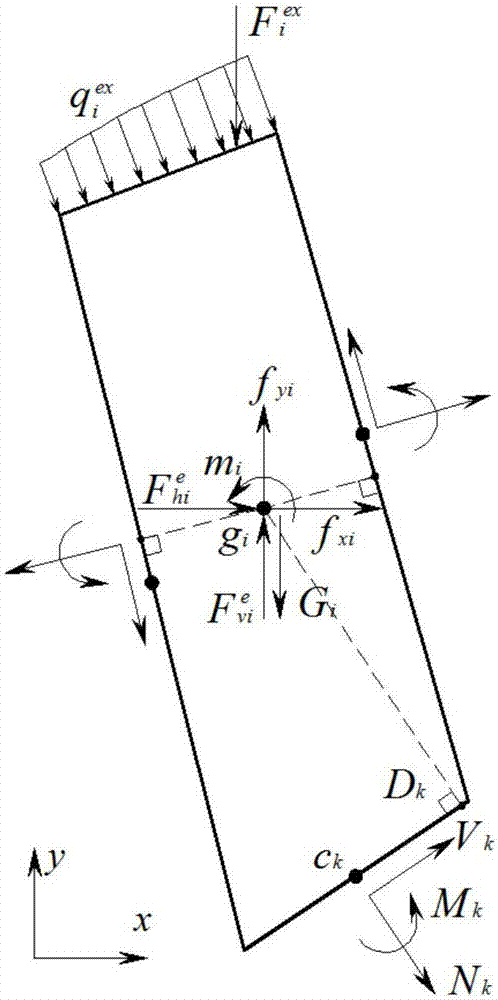
本發明是一種節理巖質邊坡傾倒破壞的極限承載力分析的下限方法，特別涉及一種地震力作用下的巖體傾倒分析法。屬于巖質邊坡穩定性分析
技術領域：
。
背景技術：
：我國山地面積占全國國土面積的60％以上，客觀上存在著大量的巖質邊坡。同時，我國是一個地震多發國家，據大量的地震資料調查表明，在我國中西部地區由于地震誘發的巖質邊坡失穩是地震災害的主要類型，其中就邊坡的失穩破壞類型而言，節理巖質邊坡傾倒破壞的數量高居第二位，僅次于剪切滑動破壞。節理巖質邊坡傾倒破壞承載力分析已成為巖土工程領域的研究熱點之一。當地震發生時，地震荷載是隨著時間變化的動荷載，巖質邊坡體結構也會隨著地震出現相應的動力響應。目前地震作用下巖質邊坡穩定性的分析方法一般有擬靜力法、newmark滑塊分析法和地震數值分析方法等。這些方法的主要區別主要在于：地震力以什么方式作用于邊坡。擬靜力法是將地震作用簡化為水平、垂直方向的不變加速度作用，此加速度產生作用在巖土體重心的慣性力。擬靜力法由于理論簡單、計算便捷，基于擬靜力法的剛體極限平衡法被我國各行業的規范所采用。newmark滑塊分析法以屈服加速度概念為基礎，認為邊坡穩定與否取決于地震時引起的變形，通過對超過屈服加速度的那部分加速度進行時間積分可估算出邊坡的滑動位移。目前地震數值分析方法主要有有限元法、有限差分法、離散單元法、流形元法等等，這些數值方法主要基于連續或非連續的力學模型，根據地震動荷載并結合巖體材料動參數、本構關系等求解邊坡的運動方程，其可真實模擬邊坡在地震過程中的動力特征和破壞機理。由于節理巖質邊坡的復雜性和地震的隨機性，目前關于節理巖質邊坡穩定性分析的研究仍然有一些不足，具體表現在：(1)節理巖質邊坡在地震過程中有可能發生剪切滑移破壞或傾倒破壞，大部分計算分析方法只能模擬邊坡的剪切滑移破壞，不能模擬傾倒破壞；(2)巖體材料的動力本構模型還不太成熟，限制了很多數值計算方法在地震分析中的應用；(3)地震是一個動態過程，巖體破壞是發生剪切滑移破壞還是傾倒破壞，其判別準則有待進一步研究；(4)巖體傾倒破壞時，采用常規的分析方法其臨界的極限狀態很難捕捉。本發明基于國家自然科學基金項目(資助編號：51564026)的研究工作，將擬靜力法、塑性極限分析下限法和數學規劃結合起來，提出了一種地震作用下節理巖質邊坡傾倒破壞極限承載能力分析的下限法技術實現要素：本發明的目的是提供一種地震作用下節理巖質邊坡傾倒破壞的極限承載能力分析方法，為節理巖質邊坡傾倒破壞分析提供一種新方法。本發明的基本原理是：以節理巖質邊坡為研究對象，根據擬靜力法原理計算巖塊形心的水平向或豎直向地震慣性力，即地震慣性力是邊坡高度、巖塊形心高度和地震參數的函數，以巖塊結構面的法向力、剪力和內力彎矩為未知量建立巖塊的力和力矩平衡方程，同時建立巖塊傾倒破壞、結構面剪切滑移、拉伸脫離的屈服條件，結合外荷載的超載系數，構建節理巖質邊坡在地震作用下發生傾倒破壞的極限承載能力的下限法線性數學規劃模型，最后采用單純形法求解邊坡傾倒破壞的極限狀態，可獲得傾倒破壞模式對應的極限荷載或強度儲備系數。本發明的技術路線如圖1所示。本發明的節理巖質邊坡傾倒破壞極限承載力分析下限法的技術方案依次按以下步驟進行：一、擬定節理巖質邊坡的計算參數根據節理巖質邊坡的實際情況，擬定需要的計算參數，主要包括：巖質邊坡的幾何參數、節理參數、巖體材料的物理力學參數(容重、凝聚力、內摩擦角、抗拉強度等)、地震荷載參數、邊坡荷載參數等信息。二、地震作用下巖塊的傾倒受力分析節理巖質邊坡中的巖體被節理切割后形成形狀不規則的巖塊，一般認為節理巖質邊坡是由巖塊和巖塊之間的結構面組成。任意一個巖塊的受力如圖2所示，相鄰巖塊結構面k的受力如圖3所示，巖塊在地震作用下受到的各種作用力包括：①巖塊i形心gi處的體積力向量fib：fib＝(0,gi,0)t(1)上式中：fib是巖塊i的體積力向量；gi是巖塊i形心gi處的自重；水平方向的體積力為0。②巖塊i形心gi處的地震慣性力向量fie：上式中：fie是巖塊i的地震慣性力向量；是巖塊i形心gi處的水平向地震慣性力；是巖塊i形心gi處的豎直向地震慣性力。③巖塊i邊界上受到集中外力fiex、分布荷載作用，其移植到巖塊i形心gi處形成等效荷載力向量fi：fi＝(fxi,fyi,mi)t(3)上式中：fxi是形心處沿x方向的等效外力，fyi是形心處沿y方向的等效外力，mi是外力等效彎矩(規定逆時針為正向)。④相鄰巖塊之間的結構面k形心ck上的內力向量qk：qk＝(nk,vk,mk)t(4)上式中：nk是沿結構面形心ck上外法線nk方向的法向力(拉正壓負)，vk是沿結構面形心ck上切向sk方向的剪力(使塊體產生逆時針轉動為正)，mk為結構面的內力彎矩(規定逆時針為正向)。三、巖塊的地震力計算本發明采用擬靜力法模擬巖塊所受的地震力，巖塊形心處的地震慣性力是邊坡高度和巖塊形心高度的函數，巖塊受地震慣性力如圖4所示。水平向地震慣性力按下式計算：上式中：αh是水平向設計地震加速度代表值，設計烈度為7、8、9度時分別取0.1g、0.2g與0.4g；ξ為地震作用效應的折減系數，一般ξ取0.25；gi是巖塊形心gi處的自重力；αi是巖塊形心處的地震加速度分布系數。地震加速度分布系數的分布圖形如圖5所所示。當邊坡高度h≤40m時，巖塊形心gi處的地震加速度分布系數按下式計算：上式中：hi是巖塊形心至邊坡坡腳的垂直高度；h是巖質邊坡的總高度；地震設計烈度7度時am＝3.0，地震設計烈度8度時am＝2.5，地震設計烈度9度時am＝2.0。當邊坡高度40m＜h≤150m時，巖塊形心處的地震加速度分布系數按下式計算：當巖質邊坡設計烈度為8、9度時，應同時考慮水平向和豎直向的地震作用。豎直向地震慣性力按下式計算：上式中：αv是豎直向設計地震加速度代表值，四、建立地震作用下的節理巖質邊坡傾倒破壞承載能力分析下限法數學規劃模型本發明的目的是求解節理巖質邊坡在地震荷載作用下的極限狀態，根據下限定理需要建立靜力許可應力場，要建立邊坡的靜力許可應力場巖體必須滿足平衡方程、屈服條件。(1)、目標函數本發明方法將節理巖質邊坡的超載系數定義為：kf＝fcollapse/fa(9)上式中，fcollapse是極限荷載，fa是邊坡當前實際施加的外荷載，對于節理巖質邊坡，求極限狀態時其超載的外荷載可以是自重、面力、集中力或者地震荷載。根據下限定理，巖質邊坡在達到極限狀態時，需求超載系數的最大值。本發明將超載系數設為目標函數如下：maximize:kf(10)(2)、剛性塊體單元平衡方程.要建立節理巖質邊坡的傾倒破壞力學模型，需同時考慮巖塊的平動和轉動平衡方程。對于圖2所示的巖塊，其受自重、表面外荷載、相鄰巖塊的作用力以及地震荷載等的作用而保持平衡。對于含有nb個巖塊的節理巖質邊坡，其平衡方程包括力的平衡方程和力矩的平衡方程。任意巖塊i的力的平衡方程包括水平方向力的平衡方程和豎直方向力的平衡方程為：上式中：nb是邊坡中巖塊的數量；是巖塊i上的結構面的數量；αk是nk軸與x軸的夾角(逆時針為正)；kf為超載系數。任意巖塊i繞其形心gi的力矩的平衡方程為：上式中：δ1是圖2中結構面k形心ck到dk點的距離；δ2是圖2中結構面k上的dk點到巖塊i形心gi的距離(點dk為塊體單元形心gi到結構面k的垂線的垂足)。根據式(11)、式(12)對于任意一個巖塊其力和力矩平衡方程可寫為：上式中：qk＝(nk,vk,mk)t是結構面k形心ck上作用的內力向量；fi＝(fxi,fyi,mi)t是剛性塊體單元i形心gi處的等效荷載力向量；是剛性塊體單元i形心gi處的地震慣性力向量；tk是坐標轉換矩陣，(3)、結構面的屈服條件為了簡化計算，本發明假設巖塊為剛體，節理巖質邊坡的破壞只會發生在相鄰塊體單元之間的結構面上；并假設巖塊會同時發生傾倒、剪切滑移、相互脫離三種破壞模式(如圖6所示)。三種破壞模式的屈服條件分別如下：①巖塊傾倒破壞的屈服條件當相鄰巖塊發生傾倒破壞時，相鄰巖塊的結構面在極限狀態下的受力如圖7所示。巖塊有可能分別繞結構面的兩個端點d1、d2發生兩種傾倒破壞。圖8為巖塊繞d1點或d1點傾倒破壞臨界狀態下的受力圖，則結構面k的法向力和內力彎矩需滿足下式：上式中：ns是整個邊坡中結構面的數量，lk是結構面k的長度,nk是結構面k的法向力(規定以拉力為正),mk是結構面k的內力彎矩。②結構面滑移屈服條件對于任意一條結構面k(如圖3所示)，假設結構面材料為理想剛塑性材料，在局部坐標系(nk,sk)中其形心上作用有內力向量qk＝(nk,vk,mk)t，則結構面的剪切滑移破壞mohr-coulomb屈服條件為：上式中：ns是整個邊坡中結構面的數量，lk是結構面k的長度，ck是結構面的凝聚力，是結構面的內摩擦角，nk是結構面k的法向力(規定以拉力為正)，vk是結構面k的剪力。③結構面抗拉強度條件由于巖塊之間的結構面一般不能都承受拉應力(結構面抗拉強度取σt＝0)，為了保證相鄰巖塊不能相互脫離開，結構面k需滿足抗拉屈服條件：上式中：ns為整個邊坡中結構面的數量，nk為結構面k的法向力(規定以拉力為正)。將式(14)、式(15)、式(16)集成后得到巖塊同時發生傾倒、剪切滑移、相互脫離三種破壞模式的屈服條件如下：上式可寫成矩陣、向量形式如下：ckqk≤bk,(k＝1,…,ns)(18)上式中：qk＝(nk,vk,mk)t是結構面k形心ck上作用的內力向量；ck是屈服矩陣，bk是屈服條件系數矩陣，bk＝[00cklkcklk0]t。(4)、地震作用下節理巖質邊坡傾倒破壞承載力分析下限法數學規劃模型根據下限定理，綜合目標函數式(10)、平衡方程式(13)、屈服條件式(18)，則可得到地震作用下節理巖質邊坡傾倒破壞承載力分析下限法數學規劃模型：上式為巖質邊坡傾倒破壞的下限法線性數學規劃模型，在無數個傾倒破壞的靜力許可應力場中，只有使kf取最大值的靜力許可應力場才是極限狀態下的應力場。五、優化算法求解節理巖質邊坡傾倒破壞的極限承載力通過上述步驟建立了地震作用下節理巖質邊坡傾倒破壞極限承載能力分析的下限法數學規劃模型，本發明方法的求解精度主要取決于所采用的線性數學規劃求解器的求解精度，本發明采用單純形法對線性數學規劃模型進行求解。對于節理巖質邊坡，有時候除了超載系數還需要求解強度儲備系數，本發明的將強度儲備系數定義為：上式中：為結構面的凝聚力和摩擦角，為結構面進行強度折減以后的凝聚力和摩擦角。如果直接求解強度儲備系數km，式(15)mohr-coulomb屈服條件會變成非線性約束，從而導致下限法模型式(19)為非線性規劃模型。為了避免求解非線性規劃模型，本發明基于式(19)采用“迭代法”求解強度儲備系數km，迭代法具體迭代過程詳見圖1，具體方法是：在式(20)中逐步降低材料強度參數并帶入式(15)，然后使用式(19)循環求解kf，當km使得kf充分接近于1時(誤差小于0.001)即為所求的強度儲備系數的最大值。本發明采用fortran編寫了求解巖質邊坡傾倒破壞極限承載力的下限法計算程序，程序包括4個部分：①前處理：收集節理巖質邊坡中巖塊和結構面的幾何信息、地質參數、材料物理力學參數、地震荷載參數等。②構建下限法數學規劃模型：計算每個巖塊的地震荷載，根據力、力矩的平衡方程、巖塊傾倒破壞、結構面的剪切滑移破壞和拉伸破壞的屈服條件，建立坡邊坡傾倒破壞承載力分析的下限法數學規劃模型。③優化求解：采用單純形法對下限法的線性數學規劃模型進行求解，獲得巖質邊坡傾倒破壞的極限狀態；如果需要求解強度儲備系數，采用程序用迭代法循環求解強度儲備系數。④后處理：根據優化求解的結果，計算極限荷載或強度儲備系數，根據結構面的內力、材料參數計算邊坡的屈服區。本發明的特點是：本發明方法為一種求解地震作用下巖質邊坡傾倒破壞極限狀態的下限法，本方法假設巖塊為剛性體，同時考慮巖塊傾倒破壞、結構面的剪切滑移破壞和拉伸破壞，采用擬靜力法計算巖塊形心處的水平和豎直向地震慣性力，建立巖塊同時滿足平動的力的平衡方程、轉動的力矩的平衡方程，根據下限定理建立巖質邊坡傾倒破壞的靜力許可應力場，并采用單純形法求解巖質邊坡傾倒破壞的極限狀態。本發明具有以下有益效果：1、本發明方法是一種求解節理巖質邊坡傾倒破壞的方法，可同時考慮巖塊傾倒破壞、結構面的剪切滑移破壞和拉伸破壞，并同時考慮巖塊的平動、轉動的平衡，是一種求解巖質邊坡傾倒破壞的新方法。2、本發明方法最終求解的是一個線性數學規劃模型，可直接求解獲得傾倒時刻的極限狀態，相比傳統的剛體極限平衡法，此方法可以自動判別巖體結構面的滑移破壞、拉伸破壞和傾倒破壞，計算前不用對巖體的破壞形式做任何的假設。3、本發明在力、力矩的平衡方程中計入了地震慣性力荷載，地震慣性力的計算參照現行主流規范中的擬靜力法的計算原理，這便于本方法的計算結果直接應用于工程實踐。4、本發明方法有效結合了下限法理論、擬靜力法原理、巖體的平動、轉動力學效應以及數學規劃技術，是下限法在地震作用下巖質邊坡傾倒破壞分析中的一次創新。附圖說明圖1為本發明技術路線圖；圖2為地震力作用下巖塊法受力圖；圖3為相鄰巖塊之間結構面受力圖；圖4為巖塊地震慣性力示意圖；圖5為巖塊形心地震加速度分布系數示意圖；圖6為巖塊之間結構面破壞模式：傾倒破壞、剪切破壞、拉伸破壞；圖7為巖塊傾倒破壞受力示意圖；圖8為巖塊傾倒破壞極限狀態示意圖；圖9為實施例1節理巖質邊坡的幾何形狀示意圖；圖10為實施例1節理巖質邊坡7度地震作用下破壞模式示意圖；圖11為實施例1節理巖質邊坡8度地震作用下破壞模式示意圖；圖12為實施例1節理巖質邊坡9度地震作用下破壞模式示意圖。具體實施方式下面結合附圖和具體實施例對本發明作進一步說明。本發明的實施例1如下：實施例1為使用式(19)求解一個含有15個巖塊的反傾層狀節理巖質邊坡的強度儲備系數。(一)、擬定節理巖質邊坡的計算參數。圖9為實施例1節理巖質邊坡的幾何形狀示意圖。此巖質邊坡高度為28.01m，坡面傾角為70°。邊坡中有兩組節理：j1是14個平行節理面組成的成組節理，節理傾角為68°，平行節理面的間距為5m；j2是一條單一節理，節理傾角為22°。j1垂直j2，邊坡被兩組節理切割后，共形成15個巖塊，29個節理面。邊坡材料的物理力學參數詳見表1。本實施例的目的是求解邊坡在7度、8度、9度地震工況下的強度儲備系數和對應的破壞模式。表1理巖質邊坡材料的物理力學參數表材料名稱重度/(kn·m-3)黏聚力/kpa內摩擦角/(°)抗拉強度/kpa完整巖塊253000.048.01000節理面/0.030.00.0(二)、地震作用下巖塊的受力分析采用編制的計算程序，對15個巖塊的分別進行了受力分析；計算了每個巖塊的自重、巖塊形心坐標、節理面中點坐標；并將29個節理面的法向力、剪力和彎矩設為未知量，共計87個未知量。(三)、巖塊地震力計算在受力分析的基礎，分別計算了15個巖塊的地震加速度分布系數、水平向地震慣性力、豎直向地震慣性力，形成每個巖塊形心作用的地震荷載力向量。(四)、建立地震作用下的節理巖質邊坡傾倒破壞承載力分析下限法數學規劃模型在巖塊受力分析的基礎上，建立了每個巖塊的平衡方程，共計30個力的平衡方程、15個力矩平衡方程；建立了24個節理面的剪切滑移屈服條件、抗拉強度條件和15個巖塊的傾倒屈服條件，最后根據式(19)建立了地震作用下的節理巖質邊坡傾倒破壞承載力分析的下限法數學規劃模型。(五)、優化算法求解節理巖質邊坡傾倒破壞的極限承載力根據式(19)建立的下限法模型，采用編制的單純形法優化程序求解，按照圖1中迭代求解強度儲備系數的流程計算得到了7度、8度、9度地震情況下邊坡的強度儲備系數。計算結果列于表2中。通過后處理程序，計算得到了邊坡對應的破壞模式。根據表2的結果可知，在無地震作用的自然狀態下邊坡的強度儲備系數為1.356，處于穩定狀態；在7度、8度地震作用下邊坡的強度儲備系數分別為1.208和1.107，均處于穩定狀態；在9度地震作用下邊坡的強度儲備系數為0.965，說明在9度地震作用下邊坡已經發生失穩。表2節理巖質邊坡各工況的強度儲備系數計算結果計算工況強度儲備系數邊坡狀態無地震1.356穩定7度地震1.208穩定8度地震1.107穩定9度地震0.965失穩破壞圖10為實施例1節理巖質邊坡7度地震作用下破壞模式示意圖。在7度地震作用下，強度儲備系數取1.208的條件下，巖塊1、巖塊2、巖塊3、巖塊6發生剪切滑移破壞，巖塊4、巖塊5同時發生剪切滑移破壞和逆時針的傾倒破壞。巖塊9～12發生逆時針的傾倒破壞，但巖塊7、巖塊8、巖塊15的底面并未發生剪切屈服，屈服區為連通，因此巖塊7～15不會發生整體滑移破壞。圖11為實施例1節理巖質邊坡8度地震作用下破壞模式示意圖。在8度地震作用下，強度儲備系數取1.107的條件下，巖塊1、巖塊2、巖塊3發生剪切滑移破壞，巖塊4、巖塊5、巖塊6、巖塊7同時發生剪切滑移破壞和逆時針的傾倒破壞，巖塊9～15由于邊坡底面屈服區未連通，處于穩定狀態。圖12為實施例1節理巖質邊坡9度地震作用下破壞模式示意圖。在9度地震作用下，強度儲備系數取0.965的條件下，巖塊1、巖塊2、巖塊3發生剪切滑移破壞，巖塊4、巖塊5、巖塊6同時發生剪切滑移破壞和逆時針的傾倒破壞，巖塊7～15由于邊坡底面屈服區未連通，處于穩定狀態。從以上分析可知，隨著地震烈度的增大，巖塊1～巖塊5的強度儲備系數逐步變小、穩定性越來越差。當前第1頁12