一種緊框架Grouplet關聯域計算方法與流程

本發明涉及一種圖像處理方法，尤其涉及一種緊框架grouplet關聯域計算方法。

背景技術：

幾筆線條就可以勾勒出一個特征很明顯的圖形或者紋理。自然圖像一般都包含由局部方向結構構成的區域。能夠更好的表示圖像中復雜幾何信息和得到圖像的稀疏表示是圖像處理的關鍵。

小波變換可以依據局部圖像的規則性來自適應的調整圖像處理中的分辨率，因而它對于圖像的表示特別高效。然而小波基在表示幾何結構的圖像上不是最優的，因為它的方支撐不能自適應表示方向幾何屬性。curvelets，contourlets，curvelets，bnadlets，wedgelets先后被提出來用以改進這一問題，并在特定的圖像處理應用中取得了不錯的效果，然而它們在實際圖像處理的應用中的改進并沒有理論上預期的效果那么好，可能由于這些圖片的紋理結構過于復雜以致于它們的基不能很好的表示圖像。為了克服這個缺點，mallat在2008年提出grouplet變換。這是一種全新的變換，它的基可以隨著圖像在不同尺度下幾何結構的變化而變化，因而可以最大限度的利用圖像的幾何特征。同時，grouplet變換的計算是簡單的，它本身的變換方法就是一種快速計算方法。

緊框架grouplet分解包含關聯域層和系數層兩個層的計算。緊框架grouplet變換中關聯域的尋找對變換的性能有著很大的影響。緊框架grouplet變換采用了blockmatching算法來尋找關聯域，這種方法的好處是它是離散化的，可以精確反映每個像素點的變化，但是由于需要預先劃定網格，所以不能自適應的根據圖像結構選取方向，因而不能很好的表示包含復雜紋理的圖像。

技術實現要素：

本發明實施例所要解決的技術問題在于，提供一種緊框架grouplet關聯域計算方法。可降低原變換中blockmatching算法帶來的高復雜度，提高了緊框架grouplet變換的效率。

為了解決上述技術問題，本發明實施例提供了一種緊框架grouplet關聯域計算方法，包括以下步驟：

1)對輸入的圖像轉化為灰度圖；

2)對所述灰度圖grouplet分解，計算第j層系數層系數，通過線檢測算子計算最優匹配點并計算第j層關聯域層系數，其中1≤j≤j；

3)重復循環步驟2)，直到j層系數都計算完畢，其中j為給定的經驗值。

進一步地，所述線檢測算子模板使用的3×3的矩陣。

更進一步地，所述線檢測算子計算最優匹配點的公式為：

其中是以為中心二值化后的3×3圖像數據矩陣；opi[j]是檢測方向i的線檢測算子，i表示集合{+45°,0°,-45°}中的一個方向；符號j表示對應矩陣第j個位置。

更進一步地，所述線檢測算子計算最優匹配點的步驟為：

1)在第j層時，以點為中心，選取大小為3×3，像素值構成的數據矩陣bp，

2)二值化所述數據矩陣bp3×3，記矩陣bp3×3的均值為av，則當bpx,y小于為所述均值av時，bpx,y取值0，否則為1，

3)使用所述線檢測算子計算最優匹配點的公式求得點最優匹配點m，

4)計算關聯域層系數和系數層系數{dj[m],aj[m]}1≤j≤j，其中

關聯域層系數：

當j從1至j增長時，系數層系數數值由以下公式更新：

其中，a[m]表示點m處的均值系數，當j＝1時，a[m]為點m處的像素值；dj[m]表示點m處的差分系數；s[m]表示點m處支撐框架的大小，當j＝1時，s[m]＝1。當j＝j時，aj[m]由公式計算得到

5)重復循環上述步驟，至1至j層的所有點都匹配完成。

實施本發明實施例，具有如下有益效果：本發明的方法降低了blockmatching算法帶來的高復雜度，應用于緊框架grouplet變換時，將大大節省變換的時間，提高效率。

附圖說明

圖1是本發明的流程結構示意圖；

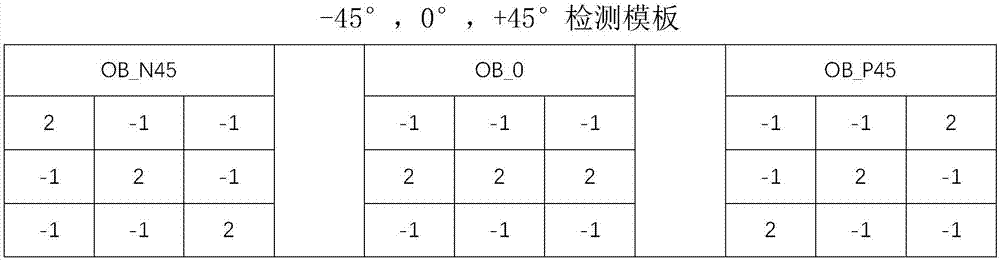
圖2是為-45°，0°，+45°檢測模板；

圖3是線檢測算法與blockmatching算法效果的對比數據。

具體實施方式

為使本發明的目的、技術方案和優點更加清楚，下面將結合附圖對本發明作進一步地詳細描述。

如圖1所示的流程結構圖。

本發明實施例的一種緊框架grouplet關聯域計算方法，包括以下步驟：①輸入圖像并轉化為灰度圖像i；②進行grouplet分解，計算j層系數層系數，通過線檢測算子計算最優匹配點并計算j層關聯域層系數；③重復循環步驟②，直到j層系數都計算完畢。

對于大小為m×n的灰度圖i，經過線檢測算子算法后將得到j層緊框架grouplet關聯域層系數aj和(j+1)系數層系數{dj[m],aj[m]}1≤j≤j。

說明:(1)ob_n45：大小為3x3的-45°檢測模板矩陣；ob_0:大小為3x3的0°檢測模板矩陣；ob_p45：大小為3x3的+45°檢測模板矩陣；(2)qm,n表示第m行，n列的點q，假設當前點為pm,n,則待匹配的點為qk,(n-1),其中k∈{m-1,m,m+1},從上到下的點依次與模板矩陣ob_n45，ob_0和ob_p45對應。(3)j為緊框架grouplet變換分解總層數；集合{dj[m],aj[m]}1≤j≤j存儲(j+1)層系數層數值；矩陣aj存儲第j層關聯域層數值。如圖2所示。

具體步驟：

(1)初始化j＝1,{dj[m],aj[m]}1≤j≤j＝0,aj＝0,m＝n＝1；

(2)pm,n為中心，選取數據矩陣bp3×3；

(3)二值化矩陣bp:記矩陣bp的均值為av,則其中正整數x,y∈[1,3]；

(4)分別將bp與線檢測模板矩陣ob_n45，ob_0，ob_p45中相應數據相乘，并將所乘結果累加后求絕對值得t1,t2,t3；min{t1,t2,t3}所對應的待匹配點即為匹配點。

(5)計算點pm,n處關聯域層系數aj(m,n)和系數層系數{dj[p],aj[p]}1≤j≤j。具體由以下公式獲得,其中點q是點p的最優匹配點：

關聯域層系數：

aj[p]＝q-p

系數層系數數值由以下公式更新：

如果m<m,就m＝m+1；

否則

如果n<n

就n＝n+1；

m＝1；

否則m＝1；n＝1；

j＝j+1；

如果j>j,結束循環，得到關聯域層系數aj和系數層系數{dj[m],aj[m]}1≤j≤j否則跳轉到步驟(2)。

實例在matlabr2014a環境下測試，本發明提出的線檢測算法計算出來的關聯域層系數同blockmatching算法一樣，都能表現出原圖像中幾何流的走向。從圖3的對比數據中可以明顯發現，在不明顯損失系數層系數稀疏度，而且可以完美重建原始圖像的前提下，本發明提出的線檢測算子匹配算法所需時間都要明顯低于使用blockmatching算法的時間。

以上所揭露的僅為本發明一種較佳實施例而已，當然不能以此來限定本發明之權利范圍，因此依本發明權利要求所作的等同變化，仍屬本發明所涵蓋的范圍。