地下水數值模擬加速方法和裝置與流程

文檔序號：11199455閱讀：514來源：國知局

本發明涉及數值模擬加速技術領域，特別是指一種地下水數值模擬加速方法和裝置。

背景技術：

研究地下水數值模擬的目的在于預測某一區域內地下水未來的動態，為評價地下水的水質與水量提供理論依據。地下水的數值模擬是將地下水流動系統進行表征、刻畫以及再現的一種有效途徑與常用工具，其不僅可以系統地分析與整理水文資料，而且能夠方便、快捷地在計算機上模擬復雜多變的地下水系統，已經成為研究地下水的一種必不可少的工具，并產生了一些優秀的地下水數值模擬軟件，如modflow、gms、mt3d、feflow、hst3d等。

地下水數值模擬采用有限差分法、有限單元法、有限體積法等數值離散方法對研究區域進行時空離散繼而建立數值模型，并將數值模型在計算機上進行模擬，這會導致巨大的數據計算量。為了解決計算量巨大的問題，已提出基于共享內存并行系統(即各處理器共享同一存儲器的多處理器系統)、基于分布式內存并行系統(即各處理器使用其各自存儲器的多處理器系統)及基于分布式共享內存并行系統(即部分處理器共享同一存儲器的多處理器系統)的基于多cpu的加速方法。這些方法對于地下水數值模擬的加速通常需要巨大、昂貴、能耗高的專業計算機。

技術實現要素：

本發明提供一種占地面積小、造價低、耗能低的地下水數值模擬加速方法和裝置。

為解決上述技術問題，本發明提供技術方案如下：

一方面，本發明提供一種地下水數值模擬加速方法，包括：

步驟1：獲取模擬區域中各模擬點(即關心點)的類型、實測參數和初始時刻水頭值，并劃分多個應力期；

步驟2：遍歷多個應力期，獲取當前應力期的長度、包含的子時間段數目和與當前應力期相關的其它數據；

步驟3：在每個應力期內，遍歷多個時間段，獲取當前時間段的長度，并將前一時間段末的水頭值存入初始水頭值組；

步驟4：在每個時間段內，根據該模擬區域的地下水參數，采用有限差分法或有限元法對描述該模擬區域地下水運動規律的偏微分方程進行離散，得到能夠反映該模擬區域中各模擬點的水頭值在時間和空間上的互相依賴關系的線性方程組；

步驟5：在每個時間段內，對于得到的線性方程組，使用線性方程組求解器進行迭代求解，直至收斂至預定精度，輸出計算結果。

進一步的，所述步驟1中，各模擬點的類型包括變水頭、定水頭和無流動，所述實測參數包括導水系數、滲透系數、給水度、貯水系數、頂面標高、底面標高和初始水頭值；步驟2中，所述與當前應力期相關的其它數據包括抽水量和補給量。

進一步的，所述步驟4包括：

步驟41：根據該模擬區域的地下水參數，采用有限差分法或有限元法對描述該模擬區域地下水運動規律的偏微分方程：

進行離散，

其中，kxx、kyy、kzz分別為滲透系數在x、y和z方向上的分量；h為水頭值；w為單位體積流量，用以代表來自源匯處的水量；ss為貯水系數；t為時間；得到一個反映該模擬區域中各模擬點的水頭值在時間和空間上的相互依賴關系的線性方程組：

其中，hcof和rhs為由步驟1獲得的模擬區域的實測參數計算得到；cc、cr、cv為滲透系數；

步驟42：將所述式(2)簡寫為[a]{h}＝{b}，并對[a]以對角格式存儲，其中，[a]為系數矩陣；{h}為水頭值向量；{b}為由已知參數項形成的已知向量。

進一步的，步驟42包括：

如果離散單元n為無流動單元，則將[a]{h}＝{b}中的a[n][n]設置為1，b[n]設置為常數，a[n][j](j≠n)設置為0；

如果離散單元n為定水頭單元，則將[a]{h}＝{b}中的a[n][n]設置為1，b[n]設置為離散單元當前的水頭值，a[n][j](j≠n)設置為0；

如果離散單元n為變水頭單元，則將[a]{h}＝{b}中的a[n][n]設置為-(hcof(n)-cc(nrb)-cc(nrh)-cr(ncd)-cr(ncf)-cv(nlz)-cv(nls))，其中，n為第n個模擬點的下標，nrb、nrh、ncd、ncf、nlz和nls分別代表第n個模擬點的上下、前后、左右周圍6個點的下標，b[n]初始時設置為rhs(n)；如果單元n的第k個鄰近單元是定水頭單元，則b[n]減去鄰近單元的滲透系數與其當前水頭值的乘積，并且a[n][n_neighbor(k)]需要置為0，其中，n_neighbor(k)為其第k個鄰近單元的下標值；如果單元n的第k個單元不是定水頭單元，則a[n][n_neighbor(k)]設置為滲透系數與其當前水頭值的乘積。

進一步的，步驟5中，所述線性方程組求解器為cusp線性方程組求解器；所述收斂的條件為水頭值變化的最大絕對值及殘差向量范數的最大絕對值均小于預定精度；所述水頭值變化的最大絕對值及殘差向量范數的最大絕對值的預定精度分別為0.0001和0.000001；所述cusp線性方程組求解器的預條件子為對角預條件子。

另一方面，本發明提供一種地下水數值模擬加速裝置，包括：

獲取模塊：用于獲取模擬區域中各模擬點的類型、實測參數和初始時刻水頭值，并劃分多個應力期；

第一遍歷模塊：用于遍歷多個應力期，獲取當前應力期的長度、所包含的子時間段數目、和與當前應力期相關的其它數據；

第二遍歷模塊：用于在每個應力期內，遍歷多個時間段，獲取當前時間段的長度，并將前一時間段末的水頭值存入初始水頭值組；

離散模塊：用于在每個時間段內，根據該模擬區域的地下水參數，采用有限差分法或有限元法對描述該模擬區域地下水運動規律的偏微分方程進行離散，得到能夠反應該模擬區域中各模擬點的水頭值在時間和空間上的相互依賴關系的線性方程組；

求解模塊：用于在每個時間段內，對得到的線性方程組，使用線性方程組求解器進行迭代求解，直至收斂至預定精度，輸出計算結果。

進一步的，獲取模塊中所述各模擬點的類型包括變水頭、定水頭和無流動，所述實測參數包括導水系數、滲透系數、給水度、貯水系數、頂面標高、底面標高和初始水頭值；第一遍歷模塊中，所述與當前應力期相關的數據包括抽水量和補給量。

進一步的，所述離散模塊包括：

離散子模塊：根據該模擬區域的地下水參數，采用有限差分法或有限元法對描述該模擬區域地下水運動規律的偏微分方程：

進行離散，

其中，hcof和rhs為由步驟1獲得的模擬區域的實測參數計算得到；cc、cr、cv為滲透系數；

存儲子模塊：將所述式(2)簡寫為[a]{h}＝{b}，并對[a]以對角格式存儲，其中，[a]為系數矩陣；{h}為水頭值向量；{b}為由已知參數項形成的已知向量；

存儲子模塊中，如果離散單元n為無流動單元，則將[a]{h}＝{b}中的a[n][n]設置為1，b[n]設置為常數，a[n][j](j≠n)設置為0；

如果離散單元n為定水頭單元，則將[a]{h}＝{b}中的a[n][n]設置為1，b[n]設置為離散單元當前的水頭值，a[n][j](j≠n)設置為0；

進一步的，求解模塊中，迭代求解線性方程組時，線性方程組求解器為cusp線性方程組求解器；所述收斂的條件為水頭值變化的最大絕對值及殘差向量范數的最大絕對值均小于預定精度；所述水頭值變化的最大絕對值及殘差向量范數的最大絕對值的預定精度分別為0.0001和0.000001；所述cusp線性方程組求解器的預條件子為對角預條件子。

進一步的，所述地下水數值模擬的加速裝置為帶有gpu的計算機或服務器，所述求解模塊由所述gpu執行。

本發明具有以下有益效果：

1)本發明根據模擬區域各關心點的不同屬性形成一個能夠反映各關心點在時間和空間上依賴關系的線性方程組，后調用高效的并行線性方程組求解器對其求解，可以提高地下水數值模擬的求解效率。

2)本發明采用基于gpu的線性方程組求解器可以使得整個地下水數值模擬過程占地更小、成本更低、能耗更小的情況下獲得更大的加速效果，在保證精度的基礎上具有較高的運行效率。

附圖說明

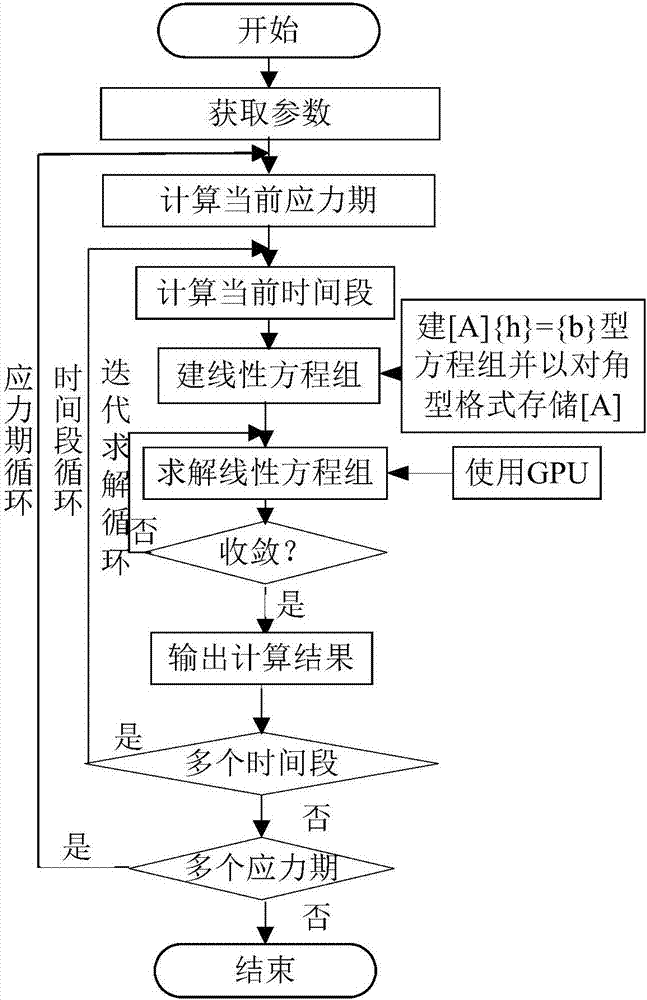
圖1為本發明的地下水數值模擬加速方法的流程圖；

圖2為本發明的地下水數值模擬加速方法的采用系數矩陣存儲格式的說明示意圖；

圖3為本發明的地下水數值模擬加速方法的一個實施例的模擬區域示意圖；

圖4為本發明的地下水數值模擬加速方法的離散后所得線性方程組系數矩陣示意圖；

圖5為采用本發明的某一實施例與一包含8個處理器的共享內存并行系統的加速比對比圖。

具體實施方式

為使本發明要解決的技術問題、技術方案和優點更加清楚，下面將結合附圖及具體實施例進行詳細描述。

一方面，本發明提供一種地下水數值模擬加速方法，如圖1～5所示，包括：

步驟1：獲取模擬區域中各模擬點(各模擬點即關心點)的類型、實測參數和初始時刻水頭值，并劃分多個應力期；各模擬點的類型包括變水頭、定水頭和無流動，所述實測參數包括導水系數、滲透系數、給水度、貯水系數、頂面標高、底面標高和初始水頭值；

步驟2：遍歷多個應力期，獲取當前應力期的長度、包含的子時間段數目和與當前應力期相關的其它數據；所述與當前應力期相關的其它數據包括抽水量和補給量；

步驟3：在每個應力期內，遍歷多個時間段，獲取當前時間段的長度，并將前一時間段末的水頭值存入初始水頭值組；

步驟4：在每個時間段內，根據該模擬區域的前面獲得的相關參數，采用有限差分法或有限元法對描述該模擬區域地下水運動規律的偏微分方程進行離散，得到能夠反映該模擬區域中各模擬點的水頭值在時間和空間上的互相依賴關系的線性方程組；

步驟5：在每個時間段內，對于得到的線性方程組，使用線性方程組求解器進行迭代求解，直至收斂至預定精度，輸出計算結果。

本發明的好處在于：

進一步的，步驟4包括：

步驟41：根據該模擬區域的地下水參數，采用有限差分法或有限元法對描述該模擬區域地下水運動規律的偏微分方程：

進行離散，

其中，hcof和rhs為由步驟1獲得的模擬區域的實測參數計算得到；cc、cr、cv為滲透系數；

步驟42：將所述式(2)簡寫為[a]{h}＝{b}，并對[a]以對角格式存儲，其中，[a]為系數矩陣；{h}為水頭值向量；{b}為由已知參數項形成的已知向量。由于地下水數值模擬的離散特點，系數矩陣[a]為一含有大量0元素的系數矩陣，在對[a]進行存儲時，可根據選定的線性方程組求解器的效率特點進行對應的存儲格式選擇，針對本發明的線性方程組求解器，如圖2所示，將[a]以dia(對角)格式用二維數組data及一維數組offsets進行存儲，以省略其它大量0的存儲，達到節省存儲空間的目的。

進一步的，步驟42包括：

如果離散單元n為無流動單元，則將[a]{h}＝{b}中的a[n][n]設置為1，b[n]設置為常數hnoflow，a[n][j](j≠n)設置為0；

如果離散單元n為定水頭單元，則將[a]{h}＝{b}中的a[n][n]設置為1，b[n]設置為離散單元當前的水頭值hnew(n)，a[n][j](j≠n)設置為0；

上述方法優選采用帶有gpu的計算機或服務器執行，步驟5的迭代求解優選由gpu執行，這樣效果更好。

實施例1：

下面以經典地下水問題twri_large為實施例對本發明作進一步描述，twri_large問題如圖3所示，其由具有不同水利傳導系數的5層組成；包含18口抽水井以及1個t型的排水系統，該排水系統使得區域中的水流向左側的定水頭邊界(一河流)。該模擬區域被劃分為40層、160行和160列，需要預測此40×160×160個模擬點在水頭、流量、流速、運動方向等滲流要素不再隨時間發生變化時的水頭值。此區域的導水系數、滲透系數、給水度、貯水系數、頂面標高、底面標高、邊界水頭值等參數數據由野外實際測量獲得。對此區域的具體模擬過程如圖1所示，為對其進行加速計算；

步驟1：利用modflow軟件讀入由野外實際測量的描述twri_large問題的邊界條件、導水系數、滲透系數、給水度、貯水系數、頂面標高、底面標高等參數數據的文件，模擬區域的大小(40層、160行、160列，即40×160×160個模擬點)、各模擬點的類型(變水頭、定水頭或者無流動)及初始時刻的水頭值(一般認為設定為0)等也以文件的形式進行讀入；

步驟2：計算每個當前應力期：

在每一個流入流出強度保持不變的應力期中，首先讀入該應力期的長度、所包含的子時間段數目。其它與此應力期有關的數據，如抽水量、補給量等也進行讀入；

步驟3：計算每個當前時間段：

在當前應力期所包含的每一個時間段中，首先計算當前時間段的長度，并將前一時間段末的水頭值存入初始水頭數組。然后采用有限差分法對模擬區域進行空間離散；

步驟4：建線性方程組：

根據讀入的數據，如果編號為n的模擬點(n按照從第1個模擬點到最后一個模擬點(第40×160×160個模擬點)的順序進行判斷)是一個無流動單元，則將差分方程[a]{h}＝{b}中的a[n][n]置為1，b[n]置為hnoflow(hnoflow為輸入文件中設定的常數999.99)，并且a[n][j](jn)也置為0；如果輸入文件中描述的編號為n的模擬點為一定水頭單元，則將差分方程[a]{h}＝{b}中的a[n][n]置為1，b[n]置為hnew(n)(hnew(n)為單元n當前的水頭值，初始由輸入文件讀入)，a[n][j](jn)置為0；如果輸入文件中描述的編號為n的模擬點為一變水頭單元，則將差分方程[a]{h}＝{b}中的a[n][n]置為-(hcof(n)-cc(nrb)-cc(nrh)-cr(ncd)-cr(ncf)-cv(nlz)-cv(nls))(hcof、cc、cv、cr均由輸入參數計算所得)，n為第n個模擬點的下標，nrb、nrh、ncd、ncf、nlz和nls分別代表第n個模擬點的上下、前后、左右周圍6個點的下標，b[n]初始時置為rhs[n](rhs也由初始輸入參數計算所得)，如果輸入文件中描述的編號為n的模擬點的第k個鄰近單元是定水頭單元(編號為n的模擬點共有上下左右前后共6個臨近單元)，則b[n]需要減去此鄰近單元的滲透系數與其當前水頭值的乘積，并且a[n][n_neighbor(k)]需要置為0(n_neighbor(k)為其第k個臨近單元的下標值)；如果第k個單元不是一定水頭單元，a[n][n_neighbor(k)]設置為其滲透系數與其當前水頭值的乘積；由此所得差分方程的系數矩陣[a]為一如圖4所示的七對角矩陣(因為模擬計算單元有上下左右前后6個鄰居，加之模擬計算單元本身形成一七對角矩陣[a])，對此七對角矩陣采用如圖2所示的dia(對角)格式用二維數組data及一維數組offsets進行存儲，以省略其它大量0的存儲，達到節省存儲空間的目的；

步驟5：迭代求解線性方程組至收斂至預定精度，輸出計算結果：

得到[a]{h}＝{b}后采用改進的基于gpu的線性方程組求解器cusp對其進行求解，具體為改進cusp中cg函數的收斂條件，即將cg函數的收斂條件改為水頭變化的最大絕對值及殘差向量范數的最大絕對值均小于輸入文件中設定的精度要求(分別為0.0001及0.000001)。同時將cg函數的預條件子選為對角預條件子；cg函數計算所得即為當前時間段結束時的水頭值；

進一步的，根據上述求解得到的水頭值，可以計算該時間段內水的流入量、流出量和累積量，并將其輸出到輸出文件，當前模擬時間、水頭值及其它有關信息也輸出到輸出文件中供用戶參考；

如果當前應力期內的所有時間段計算均已結束，所有應力期計算均已結束，整個計算過程結束。

對于實施例1，未使用本發明的計算時間/使用本發明的計算時間為10.6，即本發明的實施例1可以達到10.6倍的加速比，如圖5所示，而采用一包含8個處理器的共享內存并行系統最大僅達到5.31的加速比，使用本發明與包含8個處理器的共享內存并行系統的加速比，圖5中2.3和3.88是包含8個處理器的共享內存并行系統采用ifort及ift編譯器編譯時達到的加速比。

另一方面，本發明還提供一種地下水數值模擬加速裝置，包括：

獲取模塊：用于獲取模擬區域中各模擬點的類型、實測參數和初始時刻水頭值，并劃分多個應力期；各模擬點的類型包括變水頭、定水頭和無流動，實測參數包括導水系數、滲透系數、給水度、貯水系數、頂面標高、底面標高和初始水頭值；

第一遍歷模塊：用于遍歷多個應力期，獲取當前應力期的長度、所包含的子時間段數目、和與當前應力期相關的其它數據；與當前應力期相關的數據包括抽水量和補給量；

第二遍歷模塊：用于在每個應力期內，遍歷多個時間段，獲取當前時間段的長度，并將前一時間段末的水頭值存入初始水頭值組；

求解模塊：用于在每個時間段內，對得到的線性方程組，使用線性方程組求解器進行迭代求解，直至收斂至預定精度，輸出計算結果。

優選的，離散模塊包括：

離散子模塊：根據該模擬區域的地下水參數，采用有限差分法或有限元法對描述該模擬區域地下水運動規律的偏微分方程：

進行離散，

其中，hcof和rhs為由步驟1獲得的模擬區域的實測參數計算得到；cc、cr、cv為滲透系數；

存儲子模塊：將所述式(2)簡寫為[a]{h}＝{b}，并對[a]以對角格式存儲，其中，[a]為系數矩陣；{h}為水頭值向量；{b}為由已知參數項形成的已知向量；

存儲子模塊中，如果離散單元n為無流動單元，則將[a]{h}＝{b}中的a[n][n]設置為1，b[n]設置為常數hnoflow，a[n][j](j≠n)設置為0；

如果離散單元n為定水頭單元，則將[a]{h}＝{b}中的a[n][n]設置為1，b[n]設置為離散單元當前的水頭值hnew(n)，a[n][j](j≠n)設置為0；

優選的，求解模塊中，迭代求解線性方程組時，線性方程組求解器為cusp線性方程組求解器；收斂的條件為水頭值變化的最大絕對值及殘差向量范數的最大絕對值均小于預定精度；水頭值變化的最大絕對值及殘差向量范數的最大絕對值的預定精度分別為0.0001和0.000001；cusp線性方程組求解器的預條件子為對角預條件子。

優選的，地下水數值模擬加速裝置為帶有gpu的計算機或服務器，求解模塊由gpu執行。

綜上，本發明具有以下有益效果：

以上所述是本發明的優選實施方式，應當指出，對于本技術領域的普通技術人員來說，在不脫離本發明所述原理的前提下，還可以作出若干改進和潤飾，這些改進和潤飾也應視為本發明的保護范圍。

完整全部詳細技術資料下載

當前第1頁1 2