空間機器人由末端執行器向基座的動力學建模方法與流程
本發明涉及一種空間機器人動力學建模方法,特別涉及一種空間機器人由末端執行器向基座的動力學建模方法。
背景技術:
空間機器人具備執行在軌航天器維修、空間碎片清理等精細空間任務的能力,因而自20世紀90年代中期開始研究,至今不斷引起各航天大國及研究人員的關注。與地面機械臂不同,由于基座航天器在空間微重力環境中自由漂浮,機械臂運動對基座產生的反作用力可能會引起基座位置和姿態的顯著變化,而基座的運動反過來又會影響機械臂的運動,稱之為基座和機械臂的動力學耦合作用。這種動力學耦合作用使得與地面機械臂相比,空間機器人的動力學建模難度顯著增大。
如果忽略連桿的柔性效應,空間機器人系統可以視為多剛體系統。多剛體系統動力學建模依據原理大致可以分為基于牛頓-歐拉法和基于第二類拉格朗日方程法。其中,牛頓歐拉法下需要將系統的各個組成部分視為獨立的剛體,分別進行受力分析。而在基于拉格朗日方程下,多剛體組成的對象被視為完整的系統,通過計算系統的動能和勢能之和,并代入第二類拉格朗日方程就可得到系統的動力學方程。對于空間機器人系統,由于系統不受重力作用,因此系統的勢能為零,結合動能定理和第二類拉格朗日方程,就可以得到系統的動力學模型。這種建模方法原理清晰,反映了空間機器人的動力學特性,因而已成為大部分空間機器人研究文獻中選擇的建模方法。同時,方程中包含的與速度相關的非線性項涉及對系統慣性矩陣求導,很難直接給出解析的表達式,因而該項常常利用遞推牛頓-歐拉方法數值計算獲得。目前,基于動能定理、拉格朗日方程和遞推牛頓-歐拉法的框架建立空間機器人系統的動力學方程已經很成熟并被廣泛使用。然而需要指出的是,該方程由基座向末端執行器推導得到,即每個連桿的速度被表示為基座速度和基座與該連桿間各關節角速度的組合,因而動力學方程中包含的廣義坐標為基座速度和各關節角速度。另一方面,空間機器人的控制任務大多涉及末端執行器跟蹤期望軌跡,因為現有動力學方程中不包含末端執行器的運動變量,因而在已有的大多數空間機器人控制方法研究中,需要借助逆運動學將末端執行器的任務分解到各個關節,在關節空間下設計控制方法。本發明中,基于空間機器人系統沒有固定基座,同樣可以將末端執行器視為系統“基座”的思想,進行系統由末端執行器向基座建模,得到的動力學方程中將直接包含末端執行器的運動變量,從而有助于簡化空間機器人控制方法的研究。
技術實現要素:
針對空間機器人現有動力學模型不利于設計空間機器人末端執行器控制方法的問題,提出一種空間機器人由末端執行器向基座航天器建模的動力學建模方法,使得動力學模型中包含末端執行器的運動狀態變量,從而不需要進行逆運動學求解,可以直接針對末端執行器的運動狀態設計控制律。
本發明提出了一種空間機器人的動力學建模方法,包括定義了代表基座、末端執行器和各連桿的本體坐標系,使空間機器人系統具有對稱性;推導和建立了空間機器人由末端執行器向基座建模方式下的動力學模型;建立了得到的新模型中控制輸入與傳統由基座向末端執行器動力學建模下控制輸入的關系;最后通過在實例下對比新模型和傳統模型的作用效果驗證了本發明提出的方法的有效性。該發明的實施主要包括以下三個步驟:
步驟一、定義空間機器人基座、末端執行器和各連桿本體坐標系。
空間機器人系統是由基座航天器和n自由度的機械臂組成的多剛體系統,在動力學建模中,通過定義基座、各連桿和末端執行器的本體坐標系并實施坐標變換來描述各剛體的位姿信息。在由基座向末端執行器建模中(第i個連桿的速度由基座速度和第1~(i-1)個關節的旋轉速度計算得到),往往將基座的本體坐標系建立在其質心處。在本發明中,考慮自由漂浮的空間機器人系統沒有固定的基座,從建模的角度考慮,機械臂的末端執行器也可以視為系統的“基座”,而基座航天器則可以視為系統的“末端”,從而可以進行系統由末端執行器向基座建模(第i個連桿的速度由末端執行器速度和第(i+1)~n個關節的旋轉速度計算得到)。因為現有的建模方法中,代表末端執行器的本體坐標系大都建立在最后一個連桿的末端,本發明將基座的本體坐標系由其質心處移動至基座一端,使得空間機器人系統成為一個對稱的系統,從而由末端執行器向基座建模下得到的動力學模型將與由基座向末端執行器建模下得到的動力學模型具有相同的結構。
本發明中各剛體的本體坐標系具體定義如下:
基座和末端執行器的本體坐標系分別位于基座和最后一個連桿的末端,記為σo和σe,坐標軸選為與剛體慣量主軸平行;各連桿的本體坐標系σi位于與連桿相連的前一個關節處,z軸與關節軸重合,x軸指向與連桿相連的下一個關節或慣性張量容易計算的方向,y軸符合右手準則。在由末端執行器向基座建模時,使用同樣的坐標系集合,其中σo,σe和σi分別變為σ'e,σ'o和σ'(n-i+1)。
步驟二、建立空間機器人由末端執行器向基座建模下的動力學模型。
空間機器人由基座向末端執行器建模時,選取基座線/角速度和各個關節的轉速作為廣義變量,使用第二類拉格朗日方程可以得到系統的動力學模型如下:
其中,
通過在步驟一中適當地定義了基座、各連桿和末端執行器的本體坐標系,空間機器人系統被描述為對稱的多剛體系統。應用相同的原理,由末端執行器向基座建模得到的動力學模型將與方程(4)具有相同的結構,然而,動力學模型中的廣義變量將變為末端執行器的線/角速度和每個關節的旋轉速度:
其中,
需要指出的是,因為動力學方程由將系統的動能代入拉格朗日方程得到,而本發明在步驟一中將基座的坐標系建立在基座的一端,計算基座的動能時需要使用基座質心的線速度:
v′b=vb+ωb×a0(6)
而不是直接使用vb,a0是基座本體坐標系原點到基座質心的位置矢量,符號‘×’表示叉乘運算。同時,動力學方程中與速度相關的非線性項cb通過遞推牛頓-歐拉法數值計算得到,其中包含計算基座的慣性力,此時,需要使用基座質心的線加速度:
而不是直接使用ab。在進行由末端執行器向基座建模時,上述改動同樣適用于對末端執行器動能和慣性力的計算。
步驟三、建立兩類動力學模型中系統控制輸入的關系。
動力學方程中輸入的力和力矩包括基座控制力和力矩fb,末端執行器所受的外力、外力矩fe,以及關節作用力矩τ與
在由基座向末端執行器建模中,關節ji連接連桿bi-1和連桿bi。如果關節ji處電機對連桿bi作用的力矩為τi,顯然,同樣會對連桿bi-1作用力矩-τi。因為在由末端執行器向基座建模時,關節ji,連桿bi和bi-1分別變為關節jn-i+1,連桿bn-i和bn-i+1,引入的符號
基于同樣的原因,關節變量
本發明的有益效果是:提出了一種空間機器人由末端執行器向基座建模的動力學建模方法,其中,得到的動力學方程以末端執行器的線/角速度和各關節的轉速作為廣義變量。因為空間機器人的大多數控制任務都有關于機械臂末端執行器跟蹤期望軌跡的要求,新的動力學方程中直接包含末端執行器的運動變量,因而更方便在其基礎上設計空間機器人末端執行器相關任務的控制方法。
附圖說明
圖1空間機器人系統示意圖
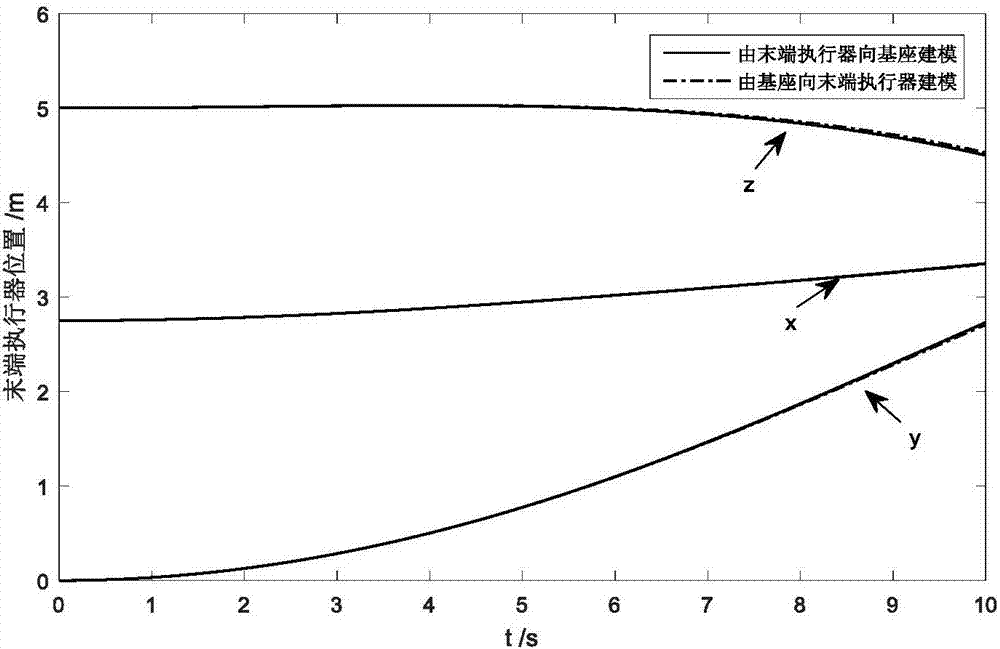
圖2兩種動力學方程下末端執行器運動軌跡
圖3兩種動力學方程下各關節角運動軌跡
具體實施方式
表1帶6自由度機械臂空間機器人的運動學/動力學參數
表1為實例中使用的空間機器人系統的運動學和動力學參數,圖1為空間機器人系統示意圖,圖2、圖3分別為兩種動力學方程下末端執行器和各關節角的運動軌跡。
以對帶6自由度機械臂的空間機器人動力學建模為例,分別使用由基座向末端執行器建模和由末端執行器向基座建模兩種方式推導系統動力學模型,將相同的作用力/作用力矩施加在兩種模型上,觀察空間機器人系統的運動情形。空間機器人的運動學/動力學參數如表1所示。
在由基座向末端執行器建模得到的動力學模型中,對基座施加作用力fb=[5,4,3]n,各關節依次施加力矩τ=-[4,3,2,1,0.5,1]n·m,末端執行器受到外力fe=[1,2,3]n;在由末端執行器向基座建模得到的動力學模型中,對“基座”(末端執行器)施加外力fb=[1,2,3]n,各關節依次施加力矩
圖2和圖3分別為兩種動力學模型下,系統施加相同的作用力/力矩后末端執行器與各關節的運動軌跡,可以看出,系統在兩種動力學建模方式下具有相同的運動狀態,其中,仿真末尾出現的微小偏差由程序數值積分誤差引起,從而說明了本發明提出的空間機器人由末端執行器向基座建模下動力學模型的正確性。
- 還沒有人留言評論。精彩留言會獲得點贊!