一種量子Haar小波變換實現量子線路設計的方法與流程

本發明涉及量子信息處理領域，具體的來說是涉及一種量子haar小波變換實現量子線路設計的方法。

背景技術：

量子計算是量子力學和計算機科學相結合的產物，量子計算的并行性、疊加性及其測量的不確定性是量子計算機優于經典計算機的根本。

量子小波變換是量子信息處理的核心算法。量子haar小波變換是一個緊致的、二階的、正交的小波變換，在信息處理領域有著廣泛的應用，例如，量子haar小波變換在圖像編碼、邊緣檢測、圖像水印等算法中有著重要作用。

在經典計算中，信息單元用比特(bit)表示，它只有兩個狀態：0態或1態。在量子計算中，信息單元用量子比特(qubit)表示，它有兩個基本量子態|0>和|1>，基本量子態簡稱為基態(basisstate)。一個量子比特可以是兩個基態的線性組合，常被稱為疊加態(superposition)，可表示為|ψ＞＝a|0>+b|1>。其中a和b是兩個復數，滿足|a|²+|b|²＝1，因此也被稱為概率幅。基態|0>和|1>，可用向量表示為：

它們的對偶向量可表示為：<0|＝[10],<1|＝[01]。

張量積(tensorproduct)是將小的向量空間合在一起，構成更大向量空間的一種方法，用符號表示，它有如下的含義：

假設u是n×n和v是m×m兩個復矩陣

那么

假設二個酉矩陣集合為：和中有m個n×n的矩陣，中有n個m×m的矩陣。擴展的張量積是一個mn×mn的矩陣其中

當中的每個矩陣都相同，aⁱ＝a，此時可寫成如果同時中的每個矩陣都相同bⁱ＝b，這時擴展的張量積退化成普通的張量積

量子線路可以由一序列的量子比特門構成，在量子線路的表示圖中，每條線都表示量子線路的連線，量子線路的執行順序是從左到右。量子比特門可以方便的用矩陣形式表示，單量子比特門可以用一個2×2的酉矩陣u表示，即u+u＝i，其中u⁺是u的共軛轉置矩陣，i是單位陣。一些基本量子比特門的名稱、符號及相應的矩陣表示見圖1。

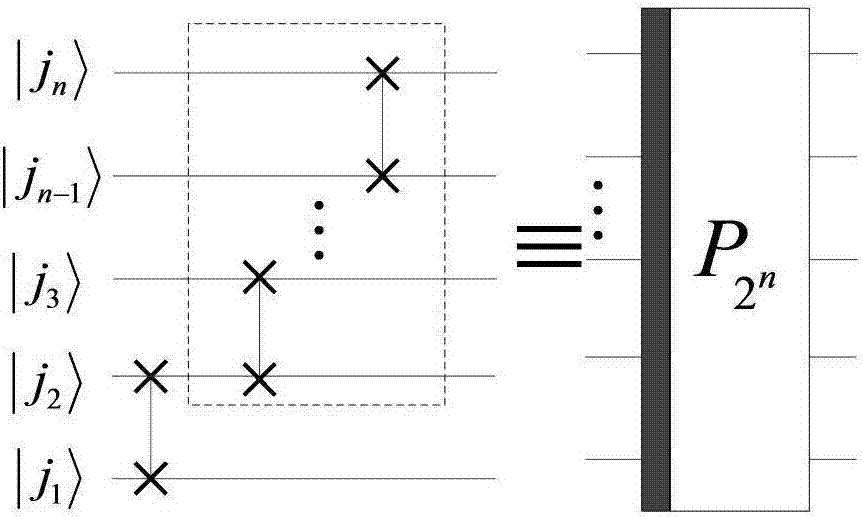
pn,m是mn×mn的均勻洗牌置換矩陣，(pn,m)k,l＝δv,z'δz,v'，其中k＝vn+z,l＝v'm+z'，0≤v,z'＜m,0≤v',z＜n，當x≠y，δx,y＝0，否者δx,y＝1。

和是兩個特殊的均勻洗牌置換矩陣，它們的遞歸方程為：

其中swap是圖1中所示的交換門，的量子實現線路如圖2所示，的量子實現線路如圖3所示。

由于現有的經典的經典的haar小波變換實現電子線路設計的復雜度為θ(n2ⁿ)，比較復雜，沒能很好滿足社會的需求。因此需要設計出復雜度更低的實現電子線路設計的方法。

技術實現要素：

本發明提供一種量子haar小波變換實現量子線路設計的方法，解決現有經典的haar小波變換實現電子線路設計的復雜度高的問題

本發明通過以下技術方案解決上述問題：

一種量子haar小波變換實現量子線路設計的方法，所述方法將量子計算與經典haar小波變換技術相結合得到量子haar小波變換；把量子haar小波變換根據擴展的張量積運算原理設計出2個量子haar小波變換和2個量子haar小波逆變換的量子線路；

2個量子haar小波變換的量子線路分別為第一個多層量子haar小波變換的量子線路和第二個多層量子haar小波變換的量子線路；

2個量子haar小波逆變換的量子線路分別為第一個多層量子haar小波逆變換的量子線路和第二個多層量子haar小波逆變換的量子線路。

上述方案中，優選的是所述第一個多層量子haar小波變換的量子線路的設計實現過程為：

設是k層2ⁿ元素的haar小波變換，是k-1層2^n-1元素的haar小波變換，則經典的多層量子haar變換可定義為：

其中是均勻洗牌置換矩陣,h和i2是圖1中單量子比特門，是i2的n次張量積。

根據擴展的張量積運算原理，得到并將它代入公式(1)，設計出第一個多層量子haar變換的迭代公式為：

其中h和i2是圖1中單量子比特門，是張量積運算符號，是i2的n次張量積，是均勻洗牌置換矩陣,是k層2ⁿ元素的haar小波變換，是k-1層2^n-1元素的haar小波變換，迭代初始值為：

假設是一個2ⁿ×2ⁿ的酉矩陣，計算張量積和可得到

根據公式(1)、(2)、(3)和(4)，當k＝n-1時，設計出復雜度為θ(n²)的第一個多層量子haar小波變換的量子線路，其中，k、n均為正整數。

上述方案中，優選的是所述第一個多層量子haar小波逆變換的量子線路的設計實現過程為：對公式(2)求逆運算，得到第一個多層量子haar小波逆變換迭代公式為：

其中h和i2是圖1中單量子比特門，是張量積運算符號，是i2的n次張量積，是均勻洗牌置換矩陣,是k層2ⁿ元素的haar小波逆變換，是k-1層2^n-1元素的haar小波逆變換，迭代初始值為：

根據公式(5)當k＝n-1時，設計出復雜度為θ(n²)的第一個多層量子haar小波逆變換的量子線路，其中，k、n均為正整數。

上述方案中，優選的是所述第二個多層量子haar小波變換的量子線路的設計實現過程為：

假設是k層2ⁿ元素的haar小波變換，是k-1層2^n-1元素的haar小波變換，則經典的多層量子haar變換可定義為：

其中是均勻洗牌置換矩陣,h和i2是圖1中單量子比特門，是i2的n次張量積。根據擴展的張量積運算原理，可化為等價的張量積將代入公式(6),設計出第二個多層量子haar變換的迭代公式為：

其中h和i2是圖1中單量子比特門，是張量積運算符號，是i2的n次張量積，是均勻洗牌置換矩陣,是k層2ⁿ元素的haar小波變換，是k-1層2^n-1元素的haar小波變換，迭代初始值為：

當k＝n-1時，設計出復雜度為θ(n²)第一個多層量子haar小波變換的量子線路，其中，k、n均為正整數。

上述方案中，優選的是第二個多層量子haar小波逆變換的量子線路的設計實現過程為：對公式(7)求逆運算，得到第二個多層量子haar小波逆變換迭代公式為：

其中h和i2是圖1中單量子比特門，是張量積運算符號，是i2的n次張量積，是均勻洗牌置換矩陣,是k層2ⁿ元素的haar小波逆變換，是k-1層2^n-1元素的haar小波逆變換，迭代初始值為：

根據公式(8)當k＝n-1時，設計出復雜度為θ(n²)的第二個多層量子haar小波逆變換的量子線路，其中，k、n均為正整數。

本發明的優點與效果是：

1、本發明與現有的量子haar小波變換實現技術相比，本發明設計了2個多層量子haar小波變換和2個多層量子haar小波逆變換的實現線路，從而構建一個相對完整的量子haar小波變換體系。而現有技術只實現了一個n-1層量子haar小波變換，本發明是對現有的量子haar小波變換實現技術的完善與改進。

2、本發明與經典的haar小波變換實現技術相比，本發明利用量子線路實現的量子haar小波變換是一種高效的變換方法，本發明設計的量子haar變換的實現線路復雜度都是θ(n²)，而經典的快速haar小波變換的實現復雜度為θ(2ⁿ)。

3、本發明適用于很多實際的信息處理應用領域，例如，圖像的壓縮、去噪、加密和解密等算法都需要高效的haar小波變換，并對量子計算理論完善和應用的推廣有重大意義。

附圖說明

圖1位本發明基本量子門和對應矩陣的表示圖；

圖2為本發明的量子實現線路圖；

圖3為本發明的量子實現線路圖；

圖4為本發明擴展張量積和的量子實現線路圖；

圖5為本發明第一個k(1≤k＜n-1)層量子haar小波變換的實現線路圖；

圖6為本發明第一個n-1層量子haar小波變換的實現線路圖；

圖7為本發明第一個k(1≤k＜n-1)層量子haar逆小波變換的實現線路圖；

圖8為本發明第一個n-1層量子haar逆小波變換的實現線路圖；

圖9為本發明第二個k(1≤k＜n-1)層量子haar小波變換的實現線路圖；

圖10為本發明第二個n-1層量子haar小波變換的實現線路圖；

圖11為本發明第二個k(1≤k＜n-1)層量子haar逆小波變換的實現線路圖；

圖12為本發明第二個n-1層量子haar逆小波變換的實現線路圖；

圖13為本發明第一個k＝1層haar小波變換的實現線路圖；

圖14為本發明第一個n-1＝2層haar小波變換的實現線路圖；

圖15為本發明第一個k＝1層haar逆小波變換的實現線路圖；

圖16為本發明第一個n-1＝2層haar逆小波變換的實現線路圖；

圖17為本發明第二個k＝1層haar小波變換的實現線路圖；

圖18為本發明第二個n-1＝2層haar小波變換的實現線路圖；

圖19為本發明第二個k＝1層haar逆小波變換的實現線路圖；

圖20為本發明第二個n-1＝2層haar逆小波變換的實現線路圖。

具體實施方式

以下結合實施例對本發明作進一步說明。

實施例1：

一種量子haar小波變換實現量子線路設計的方法，將量子計算與經典haar小波變換技術相結合得到量子haar小波變換；把量子haar小波變換根據擴展的張量積運算原理設計第一個多層量子haar小波變換的量子線路。

設是k層2ⁿ元素的haar小波變換，是k-1層2^n-1元素的haar小波變換，則經典的多層量子haar變換可定義為：

其中是均勻洗牌置換矩陣,h和i2是圖1中單量子比特門，是i2的n次張量積。

根據擴展的張量積運算原理，得到并將它代入公式(1)，設計出第一個多層量子haar變換的迭代公式為：

其中h和i2是圖1中單量子比特門，是張量積運算符號，是i2的n次張量積，是均勻洗牌置換矩陣,是k層2ⁿ元素的haar小波變換，是k-1層2^n-1元素的haar小波變換，迭代初始值為：

假設是一個2ⁿ×2ⁿ的酉矩陣，計算張量積和可得到

這兩個張量積對應的量子線路如圖4所示。

結合公式(1)、(2)、(3)和(4)，當k＝n-1時，第一個多層量子haar小波變換的量子實現線路如圖5所示，當1≤k＜n-1時，第一個多層量子haar小波變換的量子實現線路如圖6所示。由于公式(1)、(2)、(3)和(4)的換算過程中的過程主要為迭代的過程，為本領域人員公知常識，因此不在詳細把換算過程進行說明。

量子線路的復雜度是指構建量子線路的單量子比特門和雙量子比特門總的數量。由圖5和圖6知，第一個多層量子haar小波變換的量子實現線路的復雜度是θ(n²)。

本發明設計的第一個1層量子haar小波變換的實現線路如圖13所示。將n＝3和k＝1代入公式(1),得到

實現公式(9)就得到圖13中的量子線路。

本發明設計的第一個2層量子haar小波變換的實現線路如圖14所示。將n＝3和k＝n-1＝2代入公式(1),得到

實現公式(10)就得到圖14中的量子線路。

實施例2：

一種量子haar小波變換實現量子線路設計的方法，將量子計算與經典haar小波變換技術相結合得到量子haar小波變換；把量子haar小波變換根據擴展的張量積運算原理設計第一個多層量子haar小波逆變換的量子線路。

對公式(2)求逆運算，得到第一個多層量子haar小波逆變換迭代公式為：

其中h和i2是圖1中單量子比特門，是張量積運算符號，是i2的n次張量積，是均勻洗牌置換矩陣,對應的量子線路如圖3所示。是k層2ⁿ元素的haar小波逆變換，是k-1層2^n-1元素的haar小波逆變換，迭代初始值為：

根據公式(5)，當k＝n-1時，第一個多層量子haar小波逆變換的量子實現線路如圖7所示，當1≤k＜n-1時，第一個多層量子haar小波逆變換的量子實現線路如圖8所示。

由圖7和圖8知，第一個多層量子haar逆小波的量子實現線路的復雜度是θ(n²)。

本發明設計的第一個1層量子haar小波逆變換的實現線路如圖15所示。將n＝3和k＝1代入公式(4),得到

實現公式(11)就得到圖15中的量子線路。

本發明設計的第一個2層量子haar小波逆變換的實現線路如圖16所示。將n＝3和k＝n-1＝2代入公式(4),得到

實現公式(12)就得到圖16中的量子線路。

實施例3：

一種量子haar小波變換實現量子線路設計的方法，將量子計算與經典haar小波變換技術相結合得到量子haar小波變換；把量子haar小波變換根據擴展的張量積運算原理設計出第二個多層量子haar小波變換的量子線路。

假設是k層2ⁿ元素的haar小波變換，是k-1層2^n-1元素的haar小波變換，則經典的多層量子haar變換可定義為：

其中是均勻洗牌置換矩陣,h和i2是圖1中單量子比特門，是i2的n次張量積。根據擴展的張量積運算原理，可化為等價的張量積將代入公式(6),設計出第二個多層量子haar變換的迭代公式為：

其中h和i2是圖1中單量子比特門，是張量積運算符號，是i2的n次張量積，是均勻洗牌置換矩陣,是k層2ⁿ元素的haar小波變換，是k-1層2^n-1元素的haar小波變換，迭代初始值為：

當k＝n-1時，第二個多層量子haar小波變換的量子實現線路如圖9所示，當1≤k＜n-1時，第二個多層量子haar小波變換的量子實現線路如圖10所示。

由圖9和圖10知，第二個多層量子haar小波變換的量子實現線路的復雜度是θ(n²)。

本發明設計的第二個1層量子haar小波變換的實現線路如圖17所示。將n＝3和k＝1代入公式(5),得到

實現公式(13)就得到圖17中的量子線路。

本發明設計的第二個2層量子haar小波變換的實現線路如圖18所示。將n＝3和k＝n-1＝2代入公式(5),得到

實現公式(14)就得到圖18中的量子線路。

實施例4：

一種量子haar小波變換實現量子線路設計的方法，將量子計算與經典haar小波變換技術相結合得到量子haar小波變換；把量子haar小波變換根據擴展的張量積運算原理設計出第二個多層量子haar小波逆變換的量子線路。

對公式(7)求逆運算，得到第二個多層量子haar小波逆變換迭代公式為：

其中h和i2是圖1中單量子比特門，是張量積運算符號，是i2的n次張量積，是均勻洗牌置換矩陣,對應的量子線路如圖3所示。是k層2ⁿ元素的haar小波逆變換，是k-1層2^n-1元素的haar小波逆變換，迭代初始值為：

當k＝n-1時，第二個多層量子haar小波逆變換的量子實現線路如圖11所示，當1≤k＜n-1時，第二個多層量子haar小波逆變換的量子實現線路如圖12所示。

由圖11和圖12知，第二個多層量子haar小波逆變換的量子實現線路的復雜度是θ(n²)。

本發明設計的第二個1層量子haar小波逆變換的實現線路如圖19所示。將n＝3和k＝1代入公式(6),得到

實現公式(15)就得到圖19中的量子線路。

本發明設計的第二個2層量子haar小波逆變換的實現線路如圖20所示。將n＝3和k＝n-1＝2代入公式(6),得到

實現公式(16)就得到圖20中的量子線路。

以上已對本發明創造的較佳實施例進行了具體說明，但本發明并不限于實施例，熟悉本領域的技術人員在不違背本發明創造精神的前提下還可以作出種種的等同的變型或替換，這些等同的變型或替換均包含在本申請的范圍內。