基于低通過濾和決策函數的重疊社區改變點檢測方法與流程

本發明涉及復雜網絡領域。

背景技術：

目前，重疊社區發現已經揭示出網絡中不同節點間隱含的聚集關系，有助于檢測復雜系統中的功能模塊或深入理解其組織結構，是一種從靜態的角度來分析復雜網絡的方法。然而，現實中的網絡大多數是處于動態演化過程中的，其中的重疊社區也是跟隨網絡不斷演化的。正如重疊社區能揭示節點間隱含的關系一樣，網絡及其重疊社區的動態演化也蘊含許多有趣的信息或知識亟待發現。例如，通過跟蹤分析引文網絡中重疊社區的演化，人們可以知道對應某個研究領域的重疊社區發生了哪些改變，從而判斷該領域發生了何種改變。例如，重疊社區的分裂對應學科產生了分支，而增長表示該領域正在快速發展等。

總體來看，目前對重疊社區演化事件的基本類型已形成共識，并提出了重疊社區事件的檢測算法。但是，依然沒有方法檢測重疊社區改變點，即無法檢測改變的類型、改變時間和量化改變程度。另外，網絡節點的度存在著冪律分布和樞紐節點，導致重疊社區演化趨勢被高度節點掩蓋。

現有研究主要基于擴展、密度、層級聚類和統計推斷等方法實現重疊社區發現，使得重疊社區發現及分析方法客觀存在檢測準確率低、重疊節點分配錯誤率高、無法預測重疊社區未來演化等缺陷，缺乏在動態網絡環境中實現重疊社區演化分析的方法體系，成為阻礙復雜網絡中重疊社區的相關理論和應用發展的瓶頸。

技術實現要素：

重疊社區改變點檢測是網絡動態演化分析中的一項重要任務，有助于深入理解系統演化或檢測異常。目前的改變點檢測方法，例如“兩階段”法或ghrg+glr方法不能量化改變程度、無法檢測局部社區改變、對改變點的類型沒有合理分類。針對這些問題，本發明給出了一種基于低通過濾和決策函數的重疊社區改變點檢測方法，實現重疊社區的改變類型檢測和改變程度量化，克服演化趨勢被樞紐節點掩蓋的問題。

本發明技術方案：

一種復雜網絡中基于低通過濾和決策函數的重疊社區改變點檢測方法，其特征在于，首先將重疊社區所對應的子圖建模為一維社區流，使得信號處理方法能應用于重疊社區，然后通過將改變點分為兩類和基于決策函數，實現了對重疊社區改變點的檢測和量化。

有益效果

針對重疊社區改變點檢測的研究沒有考慮過量度起伏、重疊程度改變和局部演化趨勢不同等問題，實現了對重疊社區改變點的檢測和量化，有助于更深入了解復雜網絡系統的組織及系統的動態特征，從而可了解相關研究領域中已發生的變化，以及某領域是否活躍、產生分支或消失等結論。

本研究方法可應用于社會學、生物學、化學、互聯網等領域，分析重疊社區演化從而發現有用的信息或知識，具有廣闊的應用前景。

附圖說明

圖1為單社區建模過程。

圖2為兩社區建模過程。

圖3為實施例驗證步驟中，ccp(左)和pristine(右)對二元改變點的檢測結果。

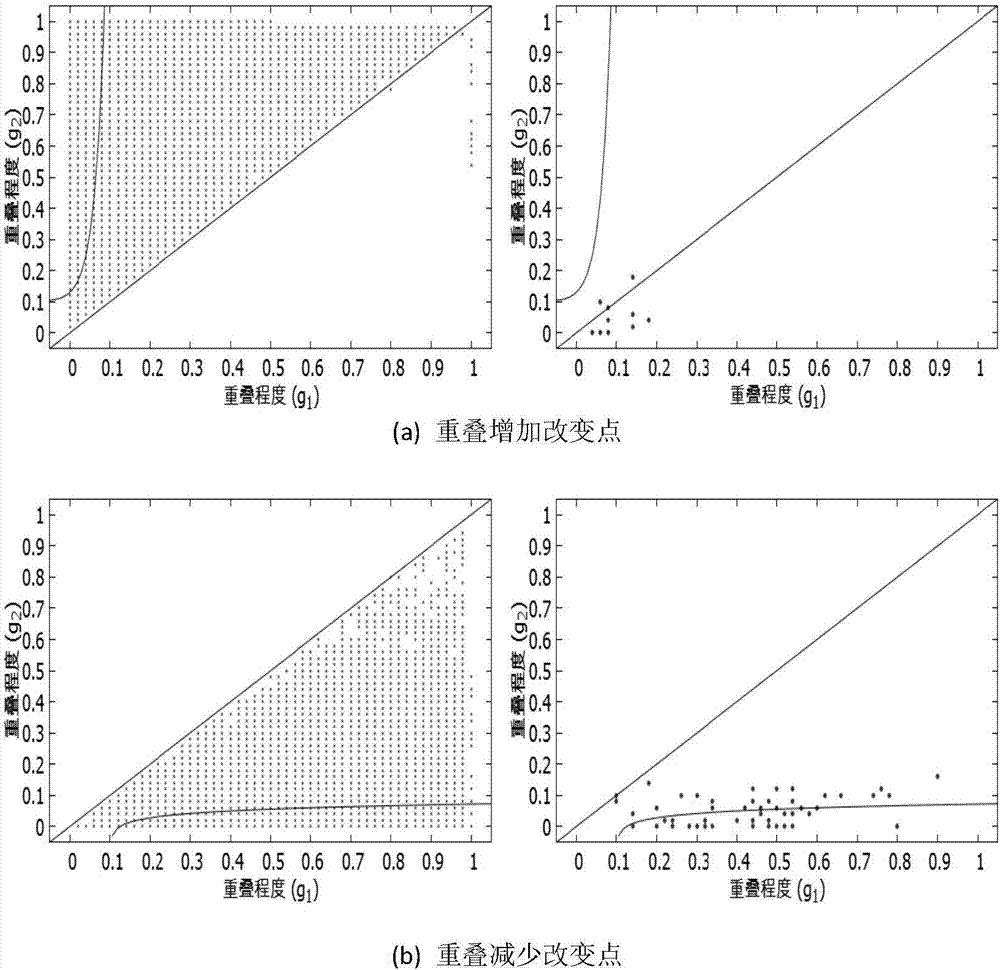
圖4為實施例驗證步驟中，ccp(左)和pristine(右)對二元改變點的檢測結果。

圖5為實施例方法流程圖。

附表說明

表1符號約定及其含義

表2二元改變點的檢測條件及改變量

具體實施方式

實施例

如圖5所示，本發明實施例基于低通過濾和決策函數的重疊社區改變點檢測方法，包括如下步驟：

步驟1.討論如何建模重疊社區子圖；

步驟2.重疊社區低通過濾；

步驟3.給出基于決策函數的改變點檢測；

步驟4.給出在合成網絡上改變點檢測的正確性驗證。

以下依次詳述。

一、社區子圖建模

本發明符號約定如表1所示。

表1

社區結構的演化較為復雜且難以準確表示。目前通常將其表示為兩個集合，然后度量二者的公共節點從而分析社區演化，但是該方法忽略了社區內部結構的變化方式。為了建模社區的動態演化，需要采用一種新的社區表示方法。首先，將一個社區所對應的子圖表示為一個鄰接矩陣。然后，按照特定方式掃描矩陣元素，構造一個長度與社區節點個數有關的一維信號，稱為社區流。這樣，信號處理領域的方法可用于處理社區流，有助于解決過量度起伏問題。

為了檢測社區ct的改變點，需比較ct在和中的拓撲結構差異。因此，首先將ct所對應的子圖表示為一個n×n的鄰接矩陣，其中的一行對應一個源節點u，一列對應目標節點v，矩陣元素為邊(u,v)上的權。如圖1所示，社區ct在增長發生前包含4個節點，其鄰接矩陣為：

其中第1‐4行(列)對應編號1‐4的節點。gt只包含了社區節點間的連接，不包含社區內節點與社區外節點的連接。由于社區成員節點可能改變，還需讓矩陣包含ct與外部節點的關系。因此，我們假設ct包含一個虛節點，代表ct的外部，然后擴展gt為g′t。以圖1為例，gt經過擴展后得到

其中，最后一行(列)對應虛節點。節點1與外部節點有兩條邊，權分別為1、2，在引入外部虛節點后，視為節點1與虛節點存在一條權為3的邊。擴展后的矩陣g′t既包含了內部節點連接，也包含與外部的連接關系。

矩陣g′t中的節點順序是任意的，因而其轉換得到的一維的社區流可以視為隨機信號，而分析該信號無意義。另外，如果更改節點編號順序，則產生另一種社區流，無法保證社區流的唯一性。因此，為了使社區對應唯一的社區流，本發明對g′t中的節點進行排列，使得g′t中的每一行元素按降序排列且方差最小。以圖1為例，g′t經過排列以后，得到新的矩陣：

排列以交換兩個節點在矩陣中的位置為基本操作，且在排列過程中，虛節點所對應的行(列)始終固定在最后。本發明將g″t中的每個矩陣元素視為一個信號，并將矩陣轉換為信號，自左向右逐行掃描g″t的元素，且跳過對角線元素。掃描g″t生成社區流的過程如圖1所示，得到了社區流x(ct)＝{4,2,1,2,1,2,3,1,1,0}。

上面討論了如何將社區建模為社區流。然而二元改變點涉及兩個社區，以上方法無法建模對應兩個社區的子圖。因此，本發明引入對兩個社區的建模方法。首先，分別為社區和構造鄰接矩陣g1和g2。然后，合并g1和g2得到

若和有公共(重疊)節點，則這些節點在g12中出現了兩次且g12忽略了和間的重疊關系。通過前面介紹的排列中的交換操作，將g1中的重疊節點移至右下角，將g2中的重疊節點移至左上角，且保證然后保留和其中的一個，得到新的矩陣

其中，g′1和g′2分別對應和中的非重疊節點，gov對應重疊節點。此時，g′12完成了對兩個社區的建模。以上所述建模過程如圖2所示。

由矩陣g′12可以看出，當社區和的重疊達到較高程度時，且此時可以認為因此，“重疊增加”在達到一定程度時可以視為“合并”，“重疊減少”與“分裂”類似。接下來，按照前面介紹過的步驟，為g′12增加一個虛節點表示兩社區的外部節點，排列節點從而保證最小方差。此處的排列過程與前面略有不同，需要保證g′1，gov和g′2之間的節點相對順序不變，得到矩陣g″12。最后，依然自左向右逐行掃描g″12，忽略對角元素、且只掃描右上角，得到對應兩個社區的社區流

二、重疊社區低通過濾

如前所述，重疊社區內存在過量度起伏問題，即高度節點與低度節點的度的差較大，高度節點容易掩蓋重疊社區總體改變。因此，需使x(ct)或變得更平滑。常用于音頻和圖像壓縮領域的子帶編碼方法，可將信號分解為一系列帶限信號(band‐limitedsignal)，稱為子帶(sub‐band)。子帶疊加之后與原信號等價，且沒有信息損失。當僅有兩個子帶時，高頻子帶代表信號的近似值而低頻子帶代表信號細節。這里也面臨著類似的問題，社區被轉換為社區流以后，也可分解為高頻和低頻子帶，分別代表社區的近似結構和細節。對x(ct)和應用低通過濾，只保留社區總體結構的近似值，去掉節點的度分布細節，可使信號平滑從而解決過量度起伏的問題。

本實施例選擇用sinc過濾器處理社區流，因為其沖擊響應是頻域中的矩形函數，是理論上最完美的過濾器且容易用算法實現。它的截止頻率由參數β指定。在頻域中sinc過濾器的沖擊響應函數為：

其中的rect(·)代表矩形函數，其定義為

社區流x(ct)和是位于空間域的。為了進行過濾，應通過傅里葉逆變換推導出sinc過濾器在空間域的沖擊響應函數，即

從而得到在空間域中的沖擊響應函數，

h(x)＝2β·sinc(2βx)(9)

其中，sinc(·)是歸一化的函數且sinc(0)＝1。至此，本實施例可以對前面得到的社區流x(ct)進行過濾，即通過在空間域中與h(x)卷積，

其中，xk(ct)表示x(ct)中的第k個值，w是限定從w個信號值的范圍中過濾的窗口值。當w＝1時，y(ct)＝x(ct)，本發明實施例通常將w設為3。另外，當n+w開始超過x(ct)的總長度時，將n+w替換為x(ct)的總長度。對于一個社區流xk(ct)，以上低通過濾的過程可以統一表示為：

所生成的一維信號y(x)保留了社區ct中節點間關系的近似信息，節點度分布的方差更小、信號波形更平滑，避免了過量度起伏問題，使得改變點更易于檢測。

三、基于決策函數的改變點檢測

盡管社區ct轉換為了社區流x(ct)，依然能從x(ct)得到社區拓撲信息。例如，社區中的節點個數n與社區流的長度|x(ct)|存在關系并且，x(ct)中位于左側的|x(ct)|-n個值取自社區內部的邊，而剩余的n個值取自與虛節點相連的邊。本發明步驟三中，將分別為一元改變點和二元改變點建立各自的決策函數進行檢測，從而得到ct的改變點集合it,t+1(ct)。

(1)一元改變點檢測

如前所述，一元改變點包括增長、收縮、消失且任何兩者不能同時成立。為了檢測這類改變點，本發明分析社區流x(ct)波形的變化，從而構造決策函數。例如，x(ct)在發生后，x(ct)波形右側升高、左側降低可能表明社區ct發生了收縮或消失事件。接下來分別針對增長、收縮和消失提出決策函數。

在傳統的“兩階段”法中，先分別在和中進行社區發現，找到最相似的社區ct和ct+1且然后通過比較ct和ct+1獲得結果。社區增長事件通常定義為在社區保持存在條件下的節點數增加。現在，假設過濾后的社區流y(ct)＝{ω1,ω2,…,ωk,ωk+1,…,ωk+n}，其中n是節點個數，因而且|y(ct)|＝k+n。社區ct的p‐value定義如下

這里的p‐value定義在y(ct)上而非x(ct)，因而避免了過量度起伏。ct存在于中可表示為pt＝p‐value(y(ct））＞η，而在演化后，社區依然存在可表示為pt+1＝p‐value(y(ct+1))＞η。因此，增長可以表示為|ct+1|＞|ct|,pt＞η且pt+1＞η，其中參數η指定重疊社區的最小p‐value。與“兩階段”法不同，本發明只需要中的重疊社區、無需中的重疊社區，并且根據ct到ct+1的拓撲改變來估計節點個數的變動。

社區成員增加通常是由周圍節點與社區新創建大量邊導致的，因而引入社區流的外部權(externalweight)，即虛節點的邊權和為：

將會增加。社區ct在中的外部權記為在中的外部權記為兩者之差可用于估計未知的ct+1相對于ct的新增節點數，并且判斷增長事件是否成立，以及量化增長的改變程度δ。綜上所述，增長改變點的決策函數為：

其中，sgn(·)當條件為真時等于1否則等于0,τ^g代表增長改變點的類型，直接采用δω^ext作為增長改變點的改變量。

與增長改變點的檢測類似，收縮類型依然定義為ct和ct+1都存在，但是應判斷成員節點是否減少。社區的成員個數減少通常是由于內部節點之間刪除大量的邊，導致p‐value減少，但是依然大于η。同樣地，為了根據ct和估計ct+1，引入社區流的內部權和(internalsum)為

因而，社區收縮用表示，其決策函數為

如前所述，收縮改變點在其改變量較大時可以視為消失改變點。因而，消失改變點的決策函數與相似。不同在于中與ct相對應的ct+1不存在，因而條件pt+1＞η應改為pt+1≤η。用于檢測消失改變點的決策函數為

在中，為了與增長、收縮具有可比性，依然用|δω^int|作為改變量δ。當得到以上決策函數之后，逐個利用和對y(ct)進行檢測，當其中一個函數檢測成功時返回對應的改變點，實現了對一元改變點的檢測和量化。

(2)二元改變點檢測

二元改變點檢測所關注的是兩社區間的重疊程度改變。如前所述，二元改變點包括重疊增加、重疊減少、合并、分裂四種類型。其中，重疊增加對應社區間公共節點的增多，重疊減少對應公共節點的減少。合并可以視為較大程度的重疊增加，因為如果兩社區的絕大部分節點都是公共節點，則將二者的并集視為一個重疊社區更合理。類似的，較大程度的重疊減少應視為分裂。與一元改變點類似，這四種類型的改變點可相互轉換且無法共存，因而歸類于二元改變點。

社區和被建模為社區流并經過低通過濾得到社區流的信號長度記為則和的公共節點數為接下來，我們按照與前面類似的方法，計算和的p‐value、內部權ω^int和外部權ω^ext等。然后，通過追蹤p‐value和重疊節點數變化實現二元改變點檢測。我們依然用邊的增減數目來估計中與間的重疊節點個數增減。假設建模和過濾過程表示為г(·)，則有如下

然后，分別計算和的p‐value如下

為了估計和相對于重疊社區和間的公共節點的變化，我們分別針對和計算δω^int和δω^ext如下

在中，原屬于的重疊社區和發生了改變，相應的p‐value為

即p′1,p′2,p′3是通過假設社區節點不變且以拓撲為依據計算得到的。我們基于決策函數并將以上統計量作為分類條件，實現二元改變點檢測。因為四個二元改變點具有內在聯系，其決策函數可以統一表示為以下形式

其中，τ可以是τ^m,τ^s,τ^oi和τ^od，分別代表合并、分裂、重疊增加和重疊減少；中對應四種改變點類型的條件表達式，總結如表2所示。

表2

在表2中，重疊增加即和的公共節點增加，表現為或的節點與外部的連接數增加，和大于0，而二者作為一個整體時，內部的連接數增加，即除此以外，還需要一個條件表示在演化發生后兩社區依然存在，即p1,p′1≥η，且不能作為一個社區存在，即p′3＜η(否則，應檢測為合并)。當以上所述的條件同時成立時，將檢測得到一個重疊增加事件。節點數改變量的估計值直接作為改變量δ。

其余三個二元改變點的檢測條件與重疊增加改變點的檢測是類似的。另外，重疊增加與合并改變點的本質是相同的，不同之處在于重疊增加發生后在中對應的社區不能視為同一個社區。完成對以上二元決策函數的推導以后，本發明列出中的所有社區對然后用以上四個二元決策函數對它們進行檢測，并返回得到的改變類型和改變量。

進一步的，本實施例以下還給出驗證步驟。

四、在合成網絡上驗證檢測改變點的正確性

分析真實世界數據前，先在合成網絡上驗證本發明方法是否正確檢測改變點。為生成這樣的網絡，采用簡化的隨機塊模型來生成包含兩個快照的一次網絡演化，記為和通過讓節點編號一致來模擬變為中社區變為社區。當檢測一元改變點時，讓只包含一個社區，社區內節點從1編號至n；也只包含一個社區，社區內節點從1編號至m。若m＞n，應該檢測到增長改變點；若m＜n，則應檢測到收縮或消失改變點。當檢測二元改變點時，分別在和中生成兩個大小相近的社區，通過改變重疊節點個數來生成不同的二元改變點。

在生成一元改變點時，讓和各包含150個節點，邊概率為0.1。和各有一個社區，節點個數分別從1變到100，社區內邊概率為0.8。這樣生成的社區易被檢測，避免了社區發現方法的影響。然后在生成的和上，分別執行ccp和pristine且假設中的社區已知、中的社區未知。當用ccp檢測時，將p‐value閾值η設為0.2，窗口大小設為w＝4，截止頻率β＝0.25。當用pristine檢測，先在上執行社區發現，得到中的社區，然后通過比較的社區與中檢測到的社區來檢測改變點，結果如圖3所示。

圖3(a)、(b)、(c)分別給出了ccp和pristine對增長、收縮和消失的檢測結果。x軸代表社區的節點個數m；y軸代表中社區的節點個數n。圖3中的每一個位置，例如(55,61)或(15,90)代表一個測試數據。直線y＝x下方的位置對應收縮改變點；y＝x上方的位置對應增長改變點；y＝x下方靠近x軸的位置對應消失改變點。在測試數據上檢測到改變點時，在該處繪一個點。

增長改變點全部檢測成功對應于直線y＝x上方空白區域被填滿。如圖3(a)，ccp檢測到了大部分增長改變點，但也將許多收縮改變點識別為增長。ccp沒有檢測到初始大小為10到20之間、增長到50個節點以上的社區。pristine只檢測到了少數增長改變點，集中于(20,20)附近。收縮改變點則應位于y＝x下方且填滿下半部分。如圖(b)，ccp檢測到的改變點幾乎都位于y＝x下方，符合預期；而pristine檢測到的收縮改變點僅集中于特定區域且將增長識別為收縮。對于消失類型改變點，如圖3(c)，ccp的結果比較符合預期且大部分靠近x軸；而pristine檢測的消失改變點遍布于所有位置，幾乎等價于隨機檢測法。

生成二元改變點時，讓和各包含兩個大小相同的社區，和中的重疊節點比例α和β均從0變到1。當α＜β時，測試數據包含重疊增加或合并；當α＞β時，包含重疊減少或分裂。然后，類似于一元改變點檢測，分別用ccp和pristine對生成的數據進行檢測。在用pristine進行改變點檢測前，執行acenv來獲得中的社區。ccp和pristine對二元改變點的檢測結果如圖4所示。

在圖4中，x軸代表中兩社區重疊節點比值α，y軸代表中的比值β，(α,β)代表重疊程度從α變為β的測試數據。在理想情況下，檢測的重疊增加應位于y＝x之上，重疊減少位于y＝x之下。靠近x軸的是分裂改變點，而靠近y軸的是合并改變點。由于合并可視為重疊增加，分裂可視為重疊減少，因而對它們不作區分。ccp和pristine的對重疊增加和重疊減少的檢結果如圖4(a)和(b)所示。ccp檢測到的重疊增加均位于y＝x上方，重疊減少也位于y＝x下方，符合預期結果。但是ccp也將少量分裂錯誤地識別為重疊增加。pristine僅檢測到少量重疊減少，無法檢測重疊增加。雖然pristine的結果很差，但是其檢測到的重疊減少改變點均正確位于y＝x下方，分裂改變點也靠近x軸。

創新點

提出了一種復雜網絡中基于低通過濾和決策函數的重疊社區改變點檢測方法，從而有助于更深入了解復雜網絡系統的組織及系統的動態特征。針對目前重疊社區改變點檢測的研究沒有考慮過量度起伏、重疊程度改變和局部演化趨勢不同等問題，給出了一種基于低通過濾的重疊社區改變點檢測方法，實現了對重疊社區改變點的檢測和量化。