基于形態學與網格構造的二值圖像校正方法與流程
本發明涉及圖像處理技術領域,特別涉及一種自帶邊框的圖像校正方法。
背景技術:
紙質資料作為日常交流的主要媒介,常用于承載重要信息。而在對紙質資料的版權認證中通常需要對紙質資料進行數字化還原,且還原精度要求較高。
在圖紙的數字化還原過程中,需要先對其進行掃描,該過程不可避免會發生幾何失真,如旋轉、縮放、非均勻形變等。而已有的圖像校正方法中,多數需要大量復雜的計算,才能檢測圖像的傾斜角解決旋轉失真,如hough變換的方法、基于fourier變換的方法和基于交叉相關性的方法。也有方法在圖像中添加定位點,通過計算掃描圖像中各個位置像素點與定位點之間的關系校正圖像。然而上述方法都難以達到精度要求。本圖像校正方法不需在圖像上添加任何標記信息,適用于對圖像還原精度要求較高的場合。
技術實現要素:
本發明提出了一種圖像校正方法,要求圖像內容自帶邊框,校正還原精度高可以達到像素級,適用于紙質資料版權保護中的數字化還原過程。
基于網格構造的二值圖像校正方法,所述方法包括:
(1)將待校正圖像掃描成灰度圖,然后將灰度圖像二值化,擬合其邊框方程。
(2)打印掃描一張校正圖,用于生成豎直及水平偏移系數表。
(3)根據待校正圖像的邊框方程及豎直、水平偏移系數表構造網格。
(4)選擇合適的閾值再次將灰度圖二值化,統計每個網格中黑白像素的數目,以確定還原后圖像中相應位置像素點的取值。
步驟(1)中,將灰度圖像二值化的閾值選擇為一個經驗值,當邊框厚度較小時,可將閾值略微調大。
步驟(1)中,擬合邊框方程,首先需要將圖像進行膨脹處理,保證邊框連續;而后利用形態學孔洞填充,找到圖像中最大的孔洞,保留其中的內容,濾除掉邊框外噪聲以免干擾邊框擬合;最后遍歷得到目標像素點集,運用最小二乘法擬合出邊框方程。
步驟(2)中,生成豎直及水平偏移系數表,包括:
(a)將校正圖打印之后,將其掃描成二值圖,擬合出其邊框方程;
(b)擬合出校正掃描圖中所有橫條矩形的橫向對稱軸,求出每一條橫向對稱軸與左右邊框的交點,計算得到豎直偏移系數表;
(c)通過豎直偏移系數表與校正掃描圖的邊框方程在該圖中生成水平網格線;
(d)擬合出校正掃描圖中所有的豎條矩形的豎向對稱軸,求出每一條豎向對稱軸與每一條水平網格線的交點,計算得到水平偏移系數表。
根據待校正圖像的邊框方程及豎直、水平偏移系數表構造網格,計算每一個網格中黑白像素點數目的比值,以確定相應位置像素點的取值,此時待校正圖像需重新選定閾值二值化。
在待校正圖像中構造網格后,將灰度圖像二值化需要對不同的閾值進行窮舉,統計校正后的圖像最外t+1層黑、白像素的數目,選擇黑白像素比值最接近t:1的二值化閾值作為最終的閾值,其中t為原始圖像邊框厚度。
本發明提出了一種圖像校正方法,利用構造網格解決打印掃描帶來的旋轉及縮放失真,利用校正圖生成豎直、水平偏移系數表解決非均勻形變失真。
附圖說明
圖1是本校正方法流程圖
圖2是形態學處理效果圖
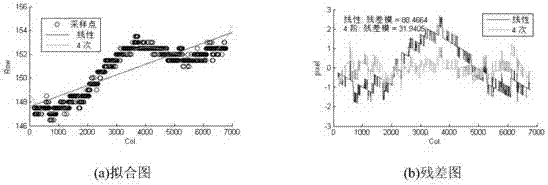
圖3是橫向邊框擬合及殘差圖
圖4是縱向邊框擬合及殘差圖
圖5是校正圖樣例
具體實施方式
圖像校正完整流程如下:
步驟1:打印校正圖計算得到豎直偏移系數表及水平偏移系數表。
步驟2:將待校正圖紙掃描成灰度圖,然后將其二值化,擬合出其邊框方程,其中上下邊框用直線擬合,左右邊框用四次曲線擬合。
步驟3:根據豎直偏移系數表及待校正圖邊框方程計算得到水平網格線lineh。
步驟4:根據lineh及水平偏移系數表計算得到每個網格中心點坐標。
步驟5:選擇合適的閾值再次將灰度圖二值化。
步驟6:根據網格中心點坐標構建網格,計算每個網格內部黑白像素點數目的比值以確定對應位置像素點還原后的取值,還原得到校正后的圖像。
將待校正圖像掃描成灰度圖,選擇經驗值將其二值化,用于擬合邊框方程。在后續校正還原中還需重新選擇閾值將其二值化。
邊框擬合,以上邊框的擬合為例:
(a)對掃描得到的圖像m進行形態學膨脹及濾波處理,得到圖m′。
(b)首先通過形態學開操作將豎直方向的像素帶濾除,然后對每一列自上而下遍歷,獲得每一列中第一個連續黑色像素序列的首尾坐標,求得其中間位置坐標,獲得采樣點集。
(c)對求得的采樣點集,運用最小二乘法進行擬合,從而獲得邊框多項式gu。
同理,可擬合出下、左、右邊框多項式gd、gl、gr。其中上下邊框可用直線擬合如圖3,左右邊框用四次曲線擬合如圖4。
設置校正圖,如圖5示。校正圖大小及位置與待校正圖像原圖保持一致,橫向邊框及縱向邊框分別為w、h個像素,邊框厚度為t(默認為奇數)。圖中除邊框外共有n1個厚度為t(與邊框一致)的橫條矩形,n2個厚度為t豎條矩形,每兩個橫條矩形相隔k1像素,上邊框與第一個橫條矩形及下邊框與最后一個橫條矩形分別相隔k1、m1像素。每兩個豎條矩形相隔k3像素,左邊框與第一個豎條矩形及右邊框與最后一個豎條矩形分別相隔k3、m3像素。
以上邊框的橫向對稱軸為x軸,左邊框的豎向對稱軸為y軸建立坐標系。設k2=k1+t、m2=m1+t。則第i個橫條矩形的橫向對稱軸(后文簡稱橫向對稱軸)方程為y=k2×i,下邊框的橫向對稱軸方程為y=n1×k2+m2。設k4=k3+t、m4=m3+t。則第j個豎條矩形的豎向對稱軸(后文簡稱豎向對稱軸)方程為x=k4×j,右邊框的豎向對稱軸方程為x=n2×k4+m4。
將校正圖經過打印掃描之后,先擬合出邊框方程,求得四個頂點左上plu(xlu,ylu)、右上pru(xru,yru)、左下pld(xld,yld)、右下prd(xrd,yrd)坐標。然后擬合出圖中所有的橫向對稱軸,得到擬合直線集
生成豎直偏移系數表ratiol(rl,y|0≤y≤h-t)、ratior(rr,y|0≤y≤h-t),以ratiol的計算為例,同理可得ratior。
當y處于第i-1條橫向對稱軸與第i條橫向對稱軸之間,即(i-1)×k2≤y≤i×k2(1≤i≤n1)時,當i取1時即y處于x軸與第一條橫向對稱軸之間。
當y處于第n1條橫向對稱軸與下邊框橫向對稱軸之間,即n1×k2≤y≤n1×k2+m2時。
其中
生成水平網格線lineh,以在校正掃描圖中構造網格線為例,用于生成水平偏移系數表,步驟如下:
i.通過ratiol、ratior及校正掃描圖的邊框方程,計算出點集pl′={p′l,i(x′l,i,y′l,i)|0≤i≤h-t}、pr′={p′r,i(x′r,i,y′r,i)|0≤i≤h-t}。p′l,i的y坐標y′l,i計算公如式(3),將其帶入到左邊框的擬合方程中(4)。即可求得x坐標x′l,i。
y′l,i=(yld-ylu)×rl,y(3)
x=a×y4+b×y3+c×y2+d×y+e(4)
ii.同理計算pr′。pl′、pr′中頂點一一對應,計算得水平網格線集
將校正圖打印掃描,在其中構造水平網格線之后,用四次曲線方程擬合該圖中所有豎向對稱軸得到擬合曲線集
豎直偏移系數表ratioh={rh,i,x|0≤i≤h-t,0≤x≤w-t}的計算如下:
當x處于第j-1條豎向對稱軸與第j條豎向對稱軸之間,即(j-1)×k4≤y≤j×k4(1≤j≤n2)時。當j取1時,x位于y軸與第一條豎向對稱軸之間。
當n2×k4≤x≤n2×k4+m4即x處于第n2條豎向對稱軸與右邊框豎向對稱軸之間。
應用偏移系數構造網格:
對于待校正圖像,先將其掃描成灰度圖選擇經驗值將其二值化,擬合其邊框方程。根據邊框方程及ratiol、ratior計算出點集pl′={(x′l,i,y′l,i)|0≤i≤h-t}、pr′={(x′r,i,y′r,i)|0≤i≤h-t},再在該圖中構造水平網格線
構造矩陣c={pc(i,j)|0≤i≤h-t,0≤j≤w-t},pc(i,j)為網格中心點坐標。其橫坐標xc(i,j)計算公式如式(7)。式(8)為水平網格線lh,i的直線方程,將xc(i,j)代入即可求得yc(i,j):
xc(i,j)=x′l,i+(x′r,i-x′l,i)×rh,i,j(7)
y=ki×x+bi(8)
構造二值圖g={gi,j|0≤i≤h-t,0≤j≤w-t},其中g(i,j)的值取決于以pc(i,j)為中心,長為(min(xru-xlu,xrd-xld))/(w-t),寬為(min(yld-ylu,yrd-yru))/(h-t)的矩形中黑白像素點數目的比值,其中min(a,b)為取較小值函數。最后在二值圖g的外層加上厚度為
灰度轉二值閾值選擇:
在網格構建完成后,需對不同的二值化閾值進行窮舉,校正還原得到的圖像最外t層應為邊框即黑色像素,第t+1層應為白色像素。統計恢復后的圖像最外t+1層黑白像素的總數,選擇黑白像素比值最接近t:1的二值化閾值作為最終的閾值。
本發明主要應用于對圖像還原精度要求較高的情況,如針對紙質資料的數字水印提取、掃描圖像與原始圖像的相關性檢測等。該方法無需添加任何定位標示,一切操作都可自動完成,無需人工輔助。
以上所述僅為本發明的實施案例,凡是未脫離本發明技術方案的內容,依據本發明的技術實質對以上實施例所做的任何簡單修改、等同變化及修飾,均仍屬于本發明技術方案保護的范圍內。
- 還沒有人留言評論。精彩留言會獲得點贊!