一種基于粒子機制免疫人群搜索的組網雷達布站方法與流程

本發明涉及一種基于粒子機制免疫人群搜索的組網雷達布站方法，屬于雷達抗干擾技術領域。

背景技術：

在高技術局部戰爭條件下，雷達裝備處于惡劣的電磁環境之中，作戰環境越來越復雜，面臨先進的反輻射導彈、電子干擾、目標隱身和低空突防所構成的“四大威脅”。單部雷達性能已經無法滿足需求，因此針對上述威脅，必須立足現有雷達，以先進的多頻段雷達和先進的計算機技術為基礎進行雷達組網，并且多部雷達組網也是今后雷達技術發展的必然趨勢之一。雷達組網是一個龐大復雜的系統工程，其目的之一是對付四大威脅，提高雷達的生存能力；二是提供高質量的目標信息給數據融合中心，提高雷達網的探測能力。

組網雷達系統中，各節點雷達的位置都影響著系統的性能，因此在提高雷達生存能力和探測能力時，需要考慮到節點雷達的位置，也就是本方法所研究的組網雷達布站問題。

孫國偉2013年在“一種新的組網雷達優化布站方法”中提出了一種基于探測概率的組網雷達優化布站方法，在分析了三種典型的組網雷達布站方式的基礎上，推導單部雷達探測概率計算方法和組網雷達聯合探測概率模型，并運用蒙特卡洛方法建模仿真得到各雷達的最佳部署位置坐標和給定高度下的最大探測面積。上述模型運用蒙特卡洛方法解決了傳統的經驗方法在求解中等規模和適度復雜性的多元積分求面積時計算量太大的問題，實現了最大探測范圍的組網雷達最優布站，但考慮到現實情況下復雜的電磁環境，以及各種樣式干擾的存在，只增大組網雷達的探測范圍已經無法滿足實際需求。

組網雷達在降低被欺騙概率的同時增大其探測范圍是一個十分復雜的實際工程問題，該問題的難點在于組網雷達的布站位置需要同時滿足最小的被欺騙概率和最大的探測范圍兩個條件，現在的尋優算法無法有效解決這一聯合優化問題，并且組網雷達系統中節點雷達布站位置也需要滿足實際條件的約束，這一帶有約束條件的優化問題在使用現有方法進行處理時變得更為復雜。因此，本文針對這一難題，提出了一種基于粒子機制免疫人群搜索的組網雷達布站方法，該方法建立被欺騙概率模型和探測范圍模型，并設計了粒子機制免疫人群搜索方法，該方法能夠在復雜約束下對組網雷達系統的被欺騙概率和探測范圍進行聯合處理，并且能夠快速準確地尋找到各節點雷達的最佳布站位置。

技術實現要素：

本發明的目的是為了提供一種基于粒子機制免疫人群搜索的組網雷達布站方法，針對欺騙干擾下組網雷達的布站問題，建立數學模型，并使用粒子機制免疫人群搜索尋找組網雷達系統中各節點雷達的最佳布站位置。

本發明的目的是這樣實現的：包括如下步驟：

步驟一：建立組網雷達在欺騙式干擾下的被欺騙概率模型和探測范圍模型；

步驟二：依照步驟一得到的模型，建立組網雷達布站的聯合優化目標函數，并確定其約束條件；

步驟三：初始化組網雷達系統的關鍵參數和搜尋隊伍的基本參數，確定粒子機制免疫人群搜索的迭代次數；

步驟四：確立適應度函數，初始化各搜尋者的個體最佳位置和搜尋隊伍的群體最佳位置；

步驟五：使用人群搜索方法制備粒子機制免疫人群搜索的疫苗；

步驟六：更新各搜尋者的位置，并對位置更新完成的搜尋隊伍進行接種疫苗操作；

步驟七：使用精英選擇和退火選擇對搜尋隊伍進行免疫選擇，并更新搜尋隊伍的群體最佳位置；

步驟八：使用人群搜索方法對早熟收斂的搜尋隊伍進行擾動；

步驟九：判斷是否滿足終止標準，若滿足終止標準，則停止搜索，輸出最優組網雷達布站位置；否則，重復步驟五到步驟九。

本發明還包括這樣一些結構特征：

1.步驟一中的被欺騙概率模型為：

其中：p組網雷達的被欺騙概率，

h0表示兩量測值zn和zm對應于真實目標的事件，h1表示對立的假設，zn和zm表示第n個節點雷達和第m個節點雷達對目標位置的測量值，變量x，y分別表示兩雷達測量值在x軸方向和y軸方向的差值，表示x軸測量差異的精度，表示y軸測量差異的精度，ρ＝ξ12/(σxσy)表示x軸測量差異與y軸測量差異的相關系數，ξ11、ξ12、ξ21、ξ22分別為協方差矩陣∑nm對應的各個矩陣元素；表示積分區間x方向的上限，表示積分區間x方向的下限，為積分區間y方向的上限，為積分區間y方向的下限；

步驟一中的探測范圍模型為：

sn＝{x|||x-xn||≤rnmax}

其中：x表示目標位置，xn表示第n個節點雷達位置，rnmax表示第n個節點雷達的最大探測距離，||·||表示2范數。

2.步驟二具體為：

最小化的被欺騙概率目標函數為：

其中：ωd為組網雷達的期望探測區域ω劃分后的子探測區域，wdi為加權系數；

最大化探測范圍的目標函數為：

其中：max表示取最大值，∪表示取并集；

聯合優化目標函數為：

約束條件為：

任意兩個節點雷達之間的布站間距d(xn,xm)滿足：

組網雷達要實現對期望探測區域ω的覆蓋：

其中，ψ為組網雷達的布站范圍，表示任意，∈表示屬于。

3.步驟三中的組網雷達系統的關鍵參數有組網雷達系統中節點雷達的個數n、期望探測區域的中心坐標x0、其半徑r、子探測區域的劃分要求、其加權系數、節點雷達的可布站范圍ψ、雷達威力半徑rnmax、兩節點雷達間的最小距離限制δrmin和組網雷達系統可接受的的最低效能費用比η0；搜尋隊伍的基本參數有粒子機制下的加速常數c1和c2、收縮因子、搜尋隊伍中搜尋者的個數m、搜尋者位置矢量的維數d以及搜尋者的最大速度vmax。

4.步驟四中的適應度函數采用最小化被欺騙概率函數和最大化探測范圍的聯合標量目標函數，為

確定各搜尋者當前位置為其初始個體最佳位置，則第i個搜尋者的個體最佳位置為pbesti＝qi，其中pbesti＝(pbesti1，pbesti2，…，pbestid)，i＝1,2,…,m，使用適應度函數計算每個搜尋者的適應值，再比較所有搜尋者的適應值，令具有最佳適應值的搜尋者的位置為搜尋隊伍的群體最佳位置gbest＝(gbest1，gbest2，…，gbestd)。

5.步驟六具體為：

將搜尋者視為粒子，使用粒子演進機制來對搜尋隊伍中搜尋者的位置和速度進行更新，t表示當前迭代次數，則搜尋隊伍中第i個搜尋者(i≤m)，第j維(j≤d)的速度更新公式為：

vij(t+1)＝γ*{vij(t)+c1×rand×(pbestij-qi,j(t))+c2×rand×(gbestj-qi,j(t))}

其位置更新公式為：

qi,j(t+1)＝qi,j(t)+vij(t+1)

其中，γ表示收縮因子，vij(t)表示第t次迭代時第i個搜尋者速度vi的第j維的值，qi,j(t)表示第t次迭代時第i個搜尋者位置qi的第j維的值，pbestij表示第i個搜尋者最佳個體位置pbesti的第j維的值，gbestj表示搜尋隊伍群體最佳位置gbest的第j維的值，rand表示0到1內的隨機數。

6.步驟七中的精英選擇是選擇精英粒子，比較接種疫苗前搜尋者的適應值和接種疫苗后搜尋者的適應值，保留適應值好的搜尋者作為精英粒子；

所述退火選擇具體為：

(1)初始化退火溫度tk；

(2)在溫度tk下重復執行以下兩個操作，直至到達溫度tk的平衡狀態：

①計算原搜尋者適應值與接種后搜尋者適應值的差值δf；

②依照概率min{1,exp(-δf/tk)}＞random[0,1]接收接種后的搜尋者，其中random[0,1]是區間[0,1]內的隨機數；

(3)退火操作：tk+1＝ctk，其中c∈(0,1)。

與現有技術相比，本發明的有益效果是：首先建立組網雷達在欺騙式干擾下的被欺騙概率模型和探測范圍模型；然后設計了粒子機制免疫人群搜索的方法，對組網雷達系統中節點雷達的布站位置進行尋優時，可以在避免其陷入局部最優的情況下快速準確地找到最優解，也就是最優的雷達布站位置。(1)由于本發明綜合考慮了組網雷達系統的被欺騙概率和探測范圍，并且以節點雷達之間的布站間距、節點雷達的威力半徑、組網雷達系統的效能費用比等工程中必須要考慮的因素，因此本發明更有利于工程實踐；(2)相比于現有的優化求解方法，本發明通過人群搜索制備疫苗，運用退火選擇和精英選擇作為免疫選擇的手段，加入人群搜索機制的擾動，能夠快速尋找到最優解，并避免陷入局部最優。

附圖說明

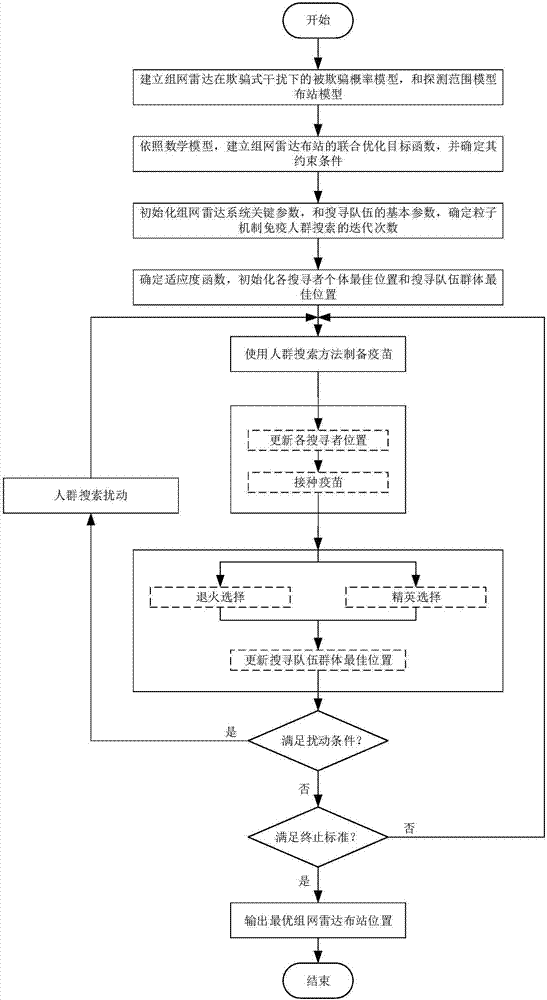
圖1為本發明實施例提供的一種基于粒子機制免疫人群搜索的組網雷達布站方法的流程示意圖。

圖2(a)、圖2(b)、圖2(c)均為利用本發明方法得到的組網雷達布站結果仿真示意圖。

圖3為粒子機制免疫人群搜索方法和粒子群優化方法的優化效果對比圖。

具體實施方式

下面結合附圖與具體實施方式對本發明作進一步詳細描述。

結合圖

本發明提供一種基于粒子機制免疫人群搜索的組網雷達布站方法，方法示意圖如圖1所示，包括以下步驟：

步驟一：建立組網雷達在欺騙式干擾下的被欺騙概率模型，和探測范圍模型。

首先，建立組網雷達探測目標的假設檢驗模型。在組網雷達系統中，zn和zm表示第n個節點雷達和第m個節點雷達對目標位置的測量值。兩個節點雷達對目標的測量值之差為δz＝zn-zm，可得測量值之差的協方差矩陣∑nm＝e[(zn-zm)(zn-zm)^t]。定義關聯距離并選用任意兩個節點雷達測量值之差的關聯距離dnm作為假設檢驗量。組網雷達系統包括n個節點雷達，n,m＝1,2,...,n，但n≠m。

兩量測值zn和zm對應于真實目標這一事件用假設h0表示，其對立的假設是h1。在h0成立的條件下，關聯距離服從χ²分布，據此可以對h0進行假設檢驗，假設檢驗為其中門限δ是由假設的顯著性水平α決定的，在高斯假設下，ε為量測數據維數，對于上述建立的組網雷達模型，ε＝2。

在h1成立的條件下，兩個節點雷達測量值之差zn-zm服從二維正態分布。其協方差矩陣為σnm，均值為e＝[ux,uy]^t，ux，uy表示第n節點雷達、第m節點雷達對目標測量值轉換到同一坐標系下的x軸和y軸坐標之差。

因此在h1成立的條件下，δz＝zn-zm的概率密度函數為：

其中變量x，y分別表示兩雷達測量值在x軸方向和y軸方向的差值，表示x軸測量差異的精度，表示y軸測量差異的精度，ρ＝ξ12/(σxσy)表示x軸測量差異與y軸測量差異的相關系數，ξ11，ξ12，ξ21，ξ22為矩陣∑nm對應的各個矩陣元素。

采用數據融合算法計算任意兩個節點雷達對測量目標的誤判概率，用積分形式來進行表示，并簡化可得

其中表示積分區間x方向的上限，表示積分區間x方向的下限，為積分區間y方向的上限，為積分區間y方向的下限。

組網雷達系統中節點雷達數n大于2，利用每兩部節點雷達對假目標進行鑒別，然后對所有的判決結果采用“取與”的原則進行融合處理，得到最終的鑒別結果即組網雷達的被欺騙概率

然后，構造組網雷達探測目標時的探測范圍模型，各節點雷達的探測范圍為sn＝{x|||x-xn||≤rnmax}，其中x表示目標位置，xn表示第n個節點雷達位置，rnmax表示第n個節點雷達的最大探測距離，||·||表示2范數。

步驟二：依照數學模型，建立組網雷達布站的聯合優化目標函數，并確定其約束條件。

首先，構建組網雷達布站的最小化被欺騙概率函數和最大化探測范圍。對組網雷達進行布站的目的是為了抑制欺騙式干擾對組網雷達的影響，即提高組網雷達在欺騙式干擾下的性能，因此需構造最小化被欺騙概率的目標函數。對組網雷達的期望探測區域ω進行劃分，得到多個子探測區域ωd，根據不同子探測區域的危險程度，對各個子探測區域ωdi賦以加權系數wdi，構造最小化的被欺騙概率目標函數為：

將各節點雷達的探測范圍進行相加，即組網雷達的探測范圍，從而構造最大化探測范圍的目標函數為：

其中，max表示取最大值，∪表示取并集。

組網雷達的優化布站問題是多目標優化問題，考慮每一個目標函數在進行尋優過程中對結果產生的影響，將其合成為一個標量目標函數，再進行優化求解。聯合優化函數為：

然后，對組網雷達進行布站，除了要考慮優化目標函數之外，還需兼顧組網雷達系統對節點雷達布站位置的約束條件，主要包括以下幾個方面：一、為保證組網雷達多視角優勢和接收目標信號之間的非相干性，兩節點雷達之間的距離不能太近；二、盡量保證對組網雷達期望探測區域的覆蓋。三、合理配置雷達，既可以確保完成任務，又可以使建網費用最低，建成的雷達網要具有較高的效能費用比。

根據組網雷達對相鄰的節點雷達之間的布站間距要求，即任意兩個節點雷達之間布站距離的約束條件d(xn,xm)≥δrmin。目標的位置坐標x為(x0,y0)，第n個節點雷達的位置坐標xn為(xn,yn)，第m個節點雷達的位置坐標xm為(xm,ym)，則任意兩個節點雷達之間的布站間距d(xn,xm)為：

組網雷達要實現對期望探測區域ω的覆蓋，即

其中，ψ為組網雷達的布站范圍，表示任意，∈表示屬于。

若采用相同雷達，即雷達費用一致，那么組網雷達探測能力的效能費用比可表示為

其中，η0表示組網雷達系統可接受的最低效能費用比。

根據上述的組網雷達布站的約束條件和所述聯合優化目標函數，構造欺騙式干擾下的組網雷達的優化式γ(x1,x2,…,xn)：

其中，s.t.表示約束條件，表示任意的。

步驟三：初始化組網雷達系統的關鍵參數，和搜尋隊伍的基本參數，確定粒子機制免疫人群搜索的迭代次數。

組網雷達系統的關鍵參數有組網雷達系統中節點雷達的個數n，期望探測區域的中心坐標x0，其半徑r，子探測區域的劃分要求，及其加權系數；節點雷達的可布站范圍ψ，雷達威力半徑rnmax，兩節點雷達間的最小距離限制δrmin，和組網雷達系統可接受的的最低效能費用比η0。

搜尋隊伍的基本參數有粒子機制下的加速常數c1和c2，收縮因子γ，搜尋隊伍中搜尋者的個數m，搜尋者位置矢量的維數d，以及搜尋者的最大速度vmax；初始化搜尋隊伍的參數信息后，要對搜尋隊伍中中各搜尋者的位置，以及速度進行初始化。

組網雷達系統中各個節點雷達的位置坐標信息集合對應于一個搜尋者的位置，雷達坐標是二維的，因此搜尋者位置矢量的維度d與節點雷達的個數n關系為d＝2×n。搜尋隊伍中第i個搜尋者的位置qi＝(qi,1,qi,2,…,qi,d)，i＝1,2,…,m，映射到二維的節點雷達的坐標為x1＝(qi,1,qi,2)，x2＝(qi,3,qi,4)，...，xn＝(qi,d-1,qi,d)。

在定義的節點雷達可布站范圍ψ內隨機產生m個搜尋者的位置q1，q2，...，qm，隨機產生各搜尋者初始速度v1，v2，...，vm，其中vi＝(vi1,vi2,…,vid)，i＝1,2,...,m。

粒子機制免疫人群搜索的迭代次數tmax，可以作為搜索的終止條件。

步驟四：確定適應度函數，初始化各搜尋者的個體最佳位置，和搜尋隊伍的群體最佳位置。

根據步驟三中搜尋者位置與節點雷達坐標的映射關系，適應度函數采用最小化被欺騙概率函數和最大化探測范圍的聯合標量目標函數，為

確定各搜尋者當前位置為其初始個體最佳位置，則第i個搜尋者的個體最佳位置為pbesti＝qi，其中pbesti＝(pbesti1，pbesti2，…，pbestid)，i＝1,2,…,m。使用適應度函數計算每個搜尋者的適應值，再比較所有搜尋者的適應值，令具有最佳適應值的搜尋者的位置為搜尋隊伍的群體最佳位置gbest＝(gbest1，gbest2，…，gbestd)。

對于約束條件的處理，采用懲罰函數法，通過給適應值添加一個懲罰因子，將原來的約束問題變為無約束問題。當搜尋者位置矢量所對應的節點雷達位置滿足約束條件時，不需要對適應度函數添加懲罰因子；當節點雷達位置不滿足約束條件時，需要對適應度函數添加一個權重為w的懲罰因子，使不滿足約束條件的搜尋者在尋優時被舍棄。

步驟五：使用人群搜索方法制備粒子機制免疫人群搜索的疫苗。

粒子機制免疫人群搜索方法使用免疫算子，有選擇、有目的地利用待求問題或求解過程中的一些特征信息或知識，提取“疫苗”并通過之后的“接種疫苗”和“免疫選擇”來指導搜索過程，提高該方法的優化性能，抑制優化過程中可能出現的退化現象。

使用人群搜索方法制備疫苗。一般來說，通過分析問題，搜索特征信息，從而根據特征信息來制作疫苗，然而，由于有時我們對待問題一時難于形成較為成熟的先驗知識，從而無法從分析問題的過程中提取出合適的特征信息，因而，得不到有效的免疫疫苗。使用進化過程中的群體最佳搜尋者來制備疫苗，因為群體最佳搜尋者仍處于進化過程中，攜帶的特征信息有限。粒子機制免疫人群搜索使用人群搜索方法，對搜索隊伍群體最佳搜尋者的位置運用人群搜索方法計算步長進行一步搜索，使之攜帶更多的有效特征信息來作為疫苗l。

人群搜索的不確定性推理行為是利用模糊系統的逼近能力，模擬人的智能搜索行為，用以建立感知(即目標函數值)和行為之間的聯系。采用高斯隸屬函數表示搜索步長模糊變量：

其中，ua為高斯隸屬度，z為輸入變量；u、β為隸屬度函數參數。當輸入變量超出[u-3β,u+3β]時，隸屬度小于0.0111；也就是說，[u-3β,u+3β]以外的元素可以忽略不計。因此，設定umin＝0.0111。

采用線性隸屬度函數，使隸屬度直接與函數值排列順序成正比，即在最佳位置有最大隸屬度值umax＝1.0，最差位置有最小隸屬度值umin＝0.0111，在其他位置u＜1.0。原函數值數列為g0，按照降序排列后為g1，降序排列后數列g1中元素相應于其原來在g0中的位置用數列g表示，其中g＝(g1,g2,...)，g1表示g1中第一個元素在數列g0中的位置，則g1中第i個目標函數值的隸屬度ui為

由此可以進一步得到第j維搜索空間目標函數值i的隸屬度

uij＝rand(ui,1)(j＝1,2,...,d)

其中，d為搜索空間維數。為了模擬人的搜索行為隨機性，函數rand(ui,1)是均勻、隨機地分布在區間[ui,1]上的實數。得出不確定性推理uij后，根據不確定性推理可得步長：

其中，jij為j維搜索空間的搜索步長；βij為高斯隸屬函數參數，其值為：

βij＝a·|zmin-zmax|

a＝(tmax-t)/tmax

其中，zmin和zmax分別是同一搜尋隊伍中的最小和最大適應度函數值；a是慣性權值，隨進化代數的增加從0.9線性遞減至0.1；t和tmax分別為當前迭代次數和最大迭代次數。

僅對群體最佳搜尋者的位置進行一步搜索，此處i＝1，求得步長j＝(j11,j12,…,j1d)，制備出疫苗l＝(l1,l2,…,ld)。

l＝gbest+j，其中li＝j1i+gbesti，i＝1,2,…,d。

步驟六：更新各搜尋者的位置，并對位置更新完成的搜尋隊伍進行接種疫苗操作。

將本方法中的搜尋者視為粒子，使用粒子演進機制來對搜尋隊伍中搜尋者的位置和速度進行更新，t表示當前迭代次數，則搜尋隊伍中第i個搜尋者(i≤m)，第j維(j≤d)的速度更新公式為：

vij(t+1)＝γ*{vij(t)+c1×rand×(pbestij-qi,j(t))+c2×rand×(gbestj-qi,j(t))}

其位置更新公式為：

qi,j(t+1)＝qi,j(t)+vij(t+1)

其中，γ表示收縮因子，vij(t)表示第t次迭代時第i個搜尋者速度vi的第j維的值，qi,j(t)表示第t次迭代時第i個搜尋者位置qi的第j維的值，pbestij表示第i個搜尋者最佳個體位置pbesti的第j維的值，gbestj表示搜尋隊伍群體最佳位置gbest的第j維的值，rand表示0到1內的隨機數。

如果搜尋者的速度過快，可能會導致在進行尋優時遺漏掉最優點，因此當更新完的速度超過規定的最大速度值vmax，或是低于最小速度-vmax時，需要對其進行邊界處理。邊界處理采用的方法是，如果搜尋者的速度超出邊界限制時，則將其速度設置為邊界速度，即當速度大于vmax時，設置當前速度為vmax；當速度小于-vmax時，設置當前速度為-vmax。

搜尋者位置矢量可映射為節點雷達坐標，因此搜尋者的位置在進化過程中不能超出相對應的節點雷達的可布站范圍ψ，因此也需要對搜尋者位置進行邊界處理。邊界處理方法與速度的邊界處理采用相同方法。

接種疫苗，需要進行如下接種操作：(1)設置一個m×n維矩陣b(b11,b12,...,b1n,b21,b22,…,b2d,...,bm1,bm2,...,bmn)。(2)對矩陣b中的bij取區間[0,1]內的隨機數，當bij≤τ時，令bij＝1；當bij＞τ時，令bij＝0。其中τ為接種概率。(3)根據矩陣b對所有搜尋者位置進行如下處理，當bij＝0時，對搜尋者位置不做任何處理；當bij＝1時，將第i個搜尋者位置的第2j-1維和第2j維坐標替換為疫苗l中對應的第2j-1維和第2j維的坐標。

步驟七：使用精英選擇和退火選擇對搜尋隊伍進行免疫選擇，并更新搜尋隊伍的群體最佳位置。

對接種疫苗后的搜尋者進行免疫選擇。搜尋隊伍中一半的搜尋者采用精英選擇，精英選擇顧名思義就是選擇精英粒子，比較接種疫苗前搜尋者的適應值和接種疫苗后搜尋者的適應值，保留適應值較好的搜尋者(即精英粒子)。

搜尋隊伍中的其他搜尋者采用模擬退火選擇，退火操作如下：(1)初始化退火溫度tk(令k＝0)。(2)在溫度tk下重復執行以下操作，直至到達溫度tk的平衡狀態。①計算原搜尋者適應值與接種后搜尋者適應值的差值δf；②依照概率min{1,exp(-δf/tk)}＞random[0,1]接收接種后的搜尋者，其中random[0,1]是區間[0,1]內的隨機數。(3)退火操作：tk+1＝ctk，其中c∈(0,1)。

其中退火溫度控制著求解過程向最優值的優化方向進行，同時它又以概率exp(-δf/tk)來接收劣質解。

比較經過免疫選擇后搜尋隊伍的適應值，對搜尋隊伍的群體最佳位置gbest進行更新。

步驟八：使用人群搜索方法對早熟收斂的搜尋隊伍進行擾動。

為了防止搜尋隊伍陷入早熟收斂，引入擾動機制，當群體最佳位置搜尋者的適應值經過q次迭代一直保持不變時，可以認為當前搜尋隊伍已經陷入早熟收斂，定義此處的q為擾動因子。使用人群搜索機制的擾動可以將搜尋隊伍從早熟收斂狀態中解放出來，具體操作為：對當前處于群體最佳位置的搜尋者使用步驟五中的人群搜索方法計算步長，再進行一步搜索，改變此時的群體最佳搜尋者的位置，打破早熟收斂的狀態，再次進行迭代。

該步驟在整個迭代過程中只進行一次，以避免多次擾動對尋優結果造成太大誤差。

步驟九：判斷是否滿足終止標準，若滿足終止標準，則停止搜索，輸出最優組網雷達布站位置；否則，重復步驟五到步驟九。

結合圖1對其進行進一步的仿真驗證：

1.實驗場景

以四部節點雷達組成的組網雷達系統為例，對其各節點雷達的布站位置進行優化，不失一般性，設探測區域ω為圓形區域，且等半徑地分成5個子區域，每個子區域的加權系數由內到外依次增加，ωd＝{x|||x-x0||≤r}。其中x0表示探測區域的中心，r為其半徑。每個子區域，及其加權系數分別為：

設可布站范圍ψ為長方形區域：x軸變化范圍為-80km～-40km，y軸變化范圍為-80km～80km；各節點雷達的參數相同，其威力半徑rimax＝100km，測距精度70m；兩雷達之間的最小距離限制為δrmin＝10km；假設檢驗模型中顯著性水平α＝0.01，檢測門限δ＝9.21。

2.實驗內容分析

實驗一：選擇探測區域中心x0＝(0,0)，半徑r＝10km，在不同考慮情況下，可以得到四部雷達布站位置的優化結果，如圖2所示。

圖2(a)部分，考慮的僅是最大化的組網雷達探測范圍；圖2(b)部分，考慮的僅是組網雷達最小化的被欺騙概率；圖2(c)部分，綜合考慮最大化探測范圍和最小化被欺騙概率二者對雷達布站位置的影響。從圖中結果可以看出，在三種情況下雷達的布站位置均滿足約束條件，間接說明了優化結果的正確性。

實驗二：以最大化組網雷達的探測范圍為例，比較粒子機制免疫人群搜索和粒子群優化方法在進行優化求解時的收斂速度，并對比其收斂結果。實驗時的其他條件均與實驗一相同。

從圖3中可以看出，粒子機制免疫人群搜索的收斂速度，以及收斂結果均優于粒子群優化方法，能夠明顯看出粒子機制免疫人群搜索在提高了收斂速度的同時，還有效地避免收斂結果陷入局部最優。