一種輸電線路下地面場強測量方法與流程

本發明屬于輸電線路檢測技術領域，涉及一種輸電線路下地面場強測量方法。

背景技術：

輸電線路是電力系統的重要組成部分，弧垂是輸電線路運行維護的重要指標之一，其大小直接關系到線路的安全性與可靠性，必須控制在一定的范圍內。而輸電線路長時間經受自然界中覆冰、溫升和風吹等氣象的影響，使得線路的弧垂發生較大變化。弧垂過小使得桿塔荷載增大，會產生斷線、倒塔和掉串等事故；弧垂過大會使導線與地面的樹木、建筑物等發生接觸并放電，從而導致線路跳閘。

通過輸電線路下地面場強的計算可以反演出線路的弧垂大小，因此若要計算出線路實際的弧垂大小，首先需要得到輸電線路下地面場強的精確值。而實際測量中環境因素會影響導線下方的電磁場，使測量的場強數據與真實數據有所偏差，所以應盡可能排除環境因素對場強測量的影響。因此，測量數據修正技術應運而生。現有的測量技術主要基于最小二乘支持向量機修正算法，該技術能較好還原沒有受外界環境干擾的真實場強值，可以實現對輸電線路地面場強的測量與數據修正。但該技術需要準確的場強值作為數據支撐，當核函數選擇不恰當時，難以達到理想的效果。

技術實現要素：

本發明的目的在于克服上述現有技術的缺點，提供了一種輸電線路下地面場強測量方法，該方法能夠實現對輸電線路下地面場強的測量及修正。

為達到上述目的，本發明所述的輸電線路下地面場強測量方法包括以下步驟：

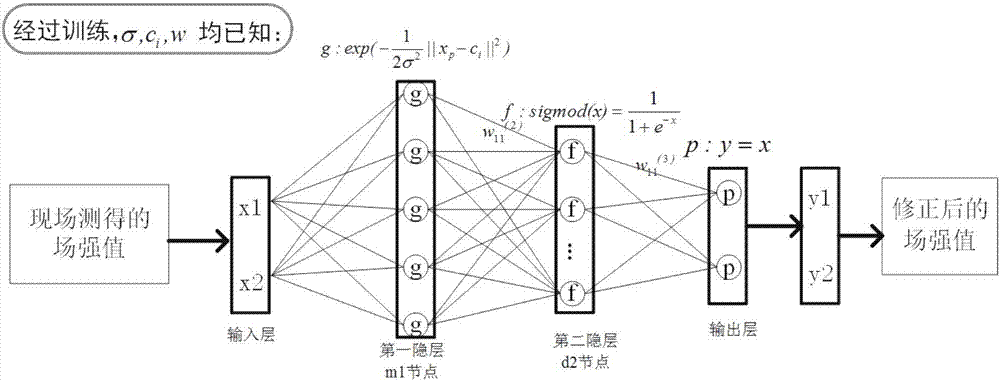
1)構建神經網絡模型，其中，所述神經網絡模型包括輸入層、第一隱層、第二隱層及輸出層，其中，輸入層與第一隱層之間及第一隱層與第二隱層之間均采用rbf神經網絡隱層模式，第二隱層與輸出層之間采用bp神經網絡隱層模式，第一隱層中各神經元節點的激勵函數均采用高斯徑向基函數，第二隱層中各神經元節點的激勵函數均采用非對稱型sigmoid函數，輸出層中各神經元節點的激勵函數均采用purelin型線性函數；

2)對步驟1)構建的神經網絡模型通過levenberg-marquardt算法進行訓練，然后根據訓練后的神經網絡模型構建測量數據修正模型；

3)獲取輸電線路下地面場強的實地測量數據，所述輸電線路下地面場強的實地測量數據通過步驟2)構建的測量數據修正模型進行修正，得輸電線路下的地面場強。

對步驟1)構建的神經網絡模型通過用levenberg-marquardt算法進行訓練的具體操作為：

1a)構建樣本庫，其中，所述樣本庫由若干輸電線路下地面場強的實測數據及若干輸電線路下地面場強的理想數據構成；

2a)從樣本庫中選取p組數據，再將p組數據中輸電線路下地面場強的實測數據作為輸入層的輸入，將p組數據中輸電線路下地面場強的理想數據作為輸出層的輸出；

3a)對神經網絡模型中的所有參數進行初始化，然后通過levenberg-marquardt算法對神經網絡模型中的所有參數進行連續訓練，并根據訓練的結果對樣本庫進行更新，直至樣本庫中各輸電線路下地面場強的實測數據與與其對應的輸電線路下地面場強的理想數據之間誤差的平均值小于等于預設值為止。

基于模擬電荷法的線路電場三維計算模型計算輸電線路下地面場強的理想數據。

基于模擬電荷法的線路電場三維計算模型計算輸電線路下地面場強的理想數據的具體操作為：將輸電線路劃分為若干線單元，再通過電位系統矩陣及輸電線路上電位的單列矩陣計算輸電線路上的電荷單列矩陣，然后根據輸電線路上電荷單列矩陣計算三維空間直角坐標系中輸電線路下地面場強的各分量，再將三維空間直角坐標系中輸電線路下地面場強的各分量進行擬合計算輸電線路下地面場強的理想數據。

本發明具有以下有益效果：

本發明所述的輸電線路下地面場強測量方法在具體操作時，基于rbf神經網絡及bp神經網絡構建神經網絡模型，然后通過levenberg-marquardt算法對神經網絡模型進行訓練，使神經網絡模型的輸入與輸出之間進行較好的擬合，然后再根據訓練后的神經網絡模型構建測量數據修正模型，并通過測量數據修正模型對實際測量得到的地面場強進行修正，從而降低外界因素對場強測試的影響，還原出最真實的輸電線路下地面場強。

附圖說明

圖1為本發明中神經網絡的訓練模型圖；

圖2為本發明中場強測量系統圖；

圖3為本發明的仿真結果圖。

具體實施方式

下面結合附圖對本發明做進一步詳細描述：

參考圖1，本發明所述的輸電線路下地面場強測量方法包括以下步驟：

1)構建神經網絡模型，其中，所述神經網絡模型包括輸入層、第一隱層、第二隱層及輸出層，其中，輸入層與第一隱層之間及第一隱層與第二隱層之間均采用rbf神經網絡隱層模式，第二隱層與輸出層之間采用bp神經網絡隱層模式，第一隱層中各神經元節點的激勵函數均采用高斯徑向基函數，第二隱層中各神經元節點的激勵函數均采用非對稱型sigmoid函數，輸出層中各神經元節點的激勵函數均采用purelin型線性函數；

2)對步驟1)構建的神經網絡模型通過用levenberg-marquardt算法進行訓練，然后訓練后的神經網絡模型構建測量數據修正模型；

3)獲取輸電線路下地面場強的實地測量數據，所述輸電線路下地面場強的實地測量數據通過步驟2)構建的測量數據修正模型進行修正，得輸電線路下的地面場強。

對步驟1)構建的神經網絡模型通過用levenberg-marquardt算法進行訓練的具體操作為：

1a)構建樣本庫，其中，所述樣本庫由若干輸電線路下地面場強的實測數據及若干輸電線路下地面場強的理想數據構成；

2a)從樣本庫中選取p組數據，再將p組數據中輸電線路下地面場強的實測數據作為輸入層的輸入，將p組數據中輸電線路下地面場強的理想數據作為輸出層的輸出；

3a)對神經網絡模型中的所有參數(包含高斯基函數的中心矢量c、基寬向量b和網絡權重系數)進行隨機初始化，并設定levenberg-marquardt算法的最大訓練步數、網絡訓練誤差及樣本測試誤差，然后通過levenberg-marquardt算法訓練神經網絡模型中的所有參數；具體訓練過程結合表1來詳細闡述：

表1

首次訓練，經過n1次的迭代，神經網絡收斂，隨后從樣本庫中選取獨立于訓練樣本的p組測試樣本，再將選取出來的p組測試樣本輸入到神經網絡中，然后計算平均測試誤差e，其中，

其中，m1為測試樣本的數量，e(n)為理想場強數據，eout(n)表示神經網絡模型輸出的修正數據；

當平均測試誤差e小于等于預設值時，則訓練結束；當平均測試誤差e大于預設值時，則將訓練樣本及測試樣本合并組成新的訓練樣本(表1中第2步，訓練樣本數更新為2p)，并將第二層的隱層節點數加2，執行步驟4a)；

4a)轉至步驟1a)，直到平均測試誤差小于等于預設值為止；

5a)網絡訓練結束，固定神經網絡的所有參數。

基于模擬電荷法的線路電場三維計算模型獲取輸電線路下地面場強的理想數據；基于模擬電荷法的線路電場三維計算模型獲取輸電線路下地面場強的理想數據的具體操作為：將輸電線路劃分為若干線單元，然后通過電位系統矩陣及輸電線路上電位的單列矩陣計算輸電線路上的電荷單列矩陣，然后根據輸電線路上電荷單列矩陣計算三維空間直角坐標系中輸電線路下地面場強的各分量，再根據三維空間直角坐標系中輸電線路下地面場強的各分量計算輸電線路下地面場強的理想數據。

圖2為本發明專利的場強測量系統圖。注意到，此時神經網絡經過訓練以后，第二隱層的節點數已經更新為d2，且網絡中的參數(高斯基函數的中心矢量c和基寬向量b和權值向量w)均為已知且固定；將現場測量得到的場強x1和x2輸入該訓練好的網絡中，其輸出y1和y2就是經過修正的場強。

圖3為本發明的仿真結果圖，在圖3中，橫坐標表示測量點與輸電導線中心線的距離，縱坐標表示該測量點出的場強值。圖3中方框表示的點為測量得到的場強值，加號表示的點為經過神經網絡后修正了的場強值，圓點為由基于模擬電荷法的三維場強模型計算而來的理想場強值。可以看出，由于環境等其他外界因素的干擾使得實際測量得到的場強數據與理想數據之間存在較大偏差，而經過網絡修正以后，測量得到的場強數據與理想數據之間能夠較好地擬合，進而實現了數據的修正。