一種基于橢圓方程的燃氣輪機部件特性線獲取方法與流程

本發明涉及的是一種燃氣輪機性能獲取方法。

背景技術：

燃氣輪機的整體性能取決于壓氣機、渦輪以及燃燒室等主要部件的特性，其中壓氣機與渦輪特性對燃氣輪機性能的影響最為關鍵。在燃氣輪機性能分析中，部件特性主要用于確定部件的運行點以及部件的進出口參數，其準確性(尤其是非設計點)將會影響性能分析的結果。通常，燃氣輪機部件特性是通過部件特性圖來進行表示，而特性圖是一般是設備生產廠商通過大量的試驗才能夠獲取，對于燃氣輪機的使用者，只能從設備生產廠商獲得少量的特性。通過實驗雖然能夠獲得準確的壓氣機特性，但是實驗費用昂貴。因此，部件特性獲取方法一直是急需解決的技術問題。

現有的基于運行數據與擬合方法確定部件特性，需要提供一個參考特性，且參考特性需與所求部件特性近似，而這個在實際中是很難獲取的，因此，該方法具有一定的實現難度。除此之外，現有方法是使用橢圓方程來擬合部件特性曲線的，而實際中不同壓氣機部件特性曲線形狀會因壓氣機結構的影響而有所不同，將導致橢圓方程擬合方法不再適合，因此，該方法的使用具有很大的局限性。

技術實現要素：

本發明的目的在于提供利用燃氣輪機運行數據獲得燃氣輪機部件特性的一種基于橢圓方程的燃氣輪機部件特性線獲取方法。

本發明的目的是這樣實現的：

本發明一種基于橢圓方程的燃氣輪機部件特性線獲取方法，其特征是：

(1)收集燃氣輪機在不同工況下的穩態運行參數，通過穩態模型計算確定不同穩態工況下的共同工作點參數，包括部件的折合流量、折合轉速、等熵效率以及壓比或者膨脹比，并且把這些參數與設計點參數相除，得到歸一化的參數值；

(2)根據獲取的不同運行工況下的共同工作點參數，對于部件的折合流量-壓比特性，對于每一個運行工況，以坐標軸原點為圓心，折合流量與壓比值確定的坐標點到圓心的距離為半徑作圓，所作的圓作為該運行工況下對應的等轉速曲線的初始曲線，n個運行工況對應n個同心圓，所有的同心圓共同形成部件的折合流量-壓比特性的初始特性圖；對于折合流量與等熵效率特性，對于每一個運行工況，以坐標軸原點為圓心，折合流量與等熵效率確定的坐標點到圓心的距離為半徑作圓，所作的圓作為該運行工況下對應的等轉速曲線的初始曲線，n個運行工況對應n個同心圓，所有的同心圓共同形成部件的折合流量-等熵效率特性的初始特性圖；

(3)把部件折合流量-壓比特性的初始特性圖以及部件折合流量-效率特性圖上的每一條等轉速線的表達式都表示成圓的參數方程，使得等轉速線上的每一點都用參數方程表示，包括之前確定的共同工作點；

(4)對于折合流量-壓比初始特性圖，對每一條等轉速線上的每一點都以等轉速線上的共同工作點為中心，引入折合流量伸縮因子以及壓比伸縮因子，對等轉速線進行伸縮變換，使得等轉速曲線從圓曲線變換到橢圓曲線，而對應的共同工作點位置保持不變；同樣，對于折合流量-等熵效率初始特性圖，對每一條等轉速線上的每一點都以線上的共同工作點為中心，引入折合流量伸縮因子和等熵效率伸縮因子，對等轉速線進行伸縮變換，使得等轉速曲線從圓曲線變換到橢圓曲線，而對應的共同工作點位置保持不變；

(5)對于步驟(4)經過伸縮變換的橢圓曲線，引入橢圓曲線的平移因子，使得橢圓曲線圍繞著共同工作點進行平移，而實現的方法是通過改變控制平移的參數角來實現平移，平移后的橢圓曲線依然經過步驟(1)確定的共同工作點；

(6)對于步驟(5)經平移之后的橢圓曲線，引入橢圓曲線的旋轉因子，使橢圓曲線繞著共同工作點進行旋轉，實現的方法是通過改變控制旋轉的參數角來實現旋轉，旋轉之后的曲線依然經過共同工作點；

(7)對于部件的折合流量-壓比特性圖上的每一條等轉速線，都有四個變換因子，即折合流量的伸縮因子、壓比的伸縮因子、曲線的平移因子以及曲線的旋轉因子，對于折合流量-效率特性圖來說，包含折合流量伸縮因子、等熵效率伸縮因子、曲線的平移因子以及曲線的旋轉因子；對于部件特性圖上的每一條等轉速線都能確定4個變換因子，把所有等轉速線對應的變換因子假設為轉速的多項式函數，從而獲得任意轉速下對應的變換因子；上述的折合流量-壓比特性圖對應的4個變換因子以及折合流量-等熵效率對應的4個變換因子，為部件特性的主系數，每個變換因子與轉速的多項式關系對應的多項式系數為子系數；

(8)把建立的部件特性圖的表達式加入到燃氣輪機仿真模型，與實際運行參數進行匹配，通過實時優化所有子系數的值，使得仿真模型的輸出運行參數與實際的運行參數一致，確定子系數的值，通過確定的子系數確定的多項式表達式，從而獲得不同等轉速線線的主系數的值，進而生成整個燃氣輪機部件特性。

本發明還可以包括：

1、折合流量的歸一化參數mi、壓比的歸一化參數πi、折合轉速的歸一化參數ni、等熵效率的歸一化參數ηi分別按下式計算：

mi＝gcor/(gcor)d；

πi＝π/πd；

ni＝ncor/(ncor)d；

ηi＝η/ηd。

2、折合流量-壓比特性曲線中任意等轉速曲線的參數方程表示為：

mi＝rcos(θ)

πi＝rsin(θ)

其中，mi、πi表示等轉速線上任意一點的折合流量與壓比，r為共同工作點到原點的距離，θ為參數角，0＜θ＜2π；

折合流量-效率特性曲線中任意等轉速曲線的參數方程表示為：

mi＝rcos(θ)

ηi＝rsin(θ)

其中，mi、ηi表示等轉速線上任意一點的折合流量與等熵效率，r為共同工作點到原點的距離，θ為參數角，0＜θ＜2π。

3、折合流量-壓比特性曲線伸縮變換對應的公式為：

m′i＝mi+(mi-mi0)sfπm

π′i＝πi+(πi-πi0)sfππ

其中，m‘i、π’i表示經過伸縮變換后等轉速曲線上任意一點的折合流量與壓比，mi0、πi0表示共同工作點對應的折合流量、壓比，sfπm和sfππ分別表示折合流量伸縮因子和壓比伸縮因子；

折合流量-效率特性曲線伸縮變換對應的公式為：

m′i＝mi+(mi-mi0)sfηm

η′i＝ηi+(ηi-ηi0)sfηη

其中，m‘i、η’i表示經過伸縮變換后等轉速曲線上任意一點的折合流量與效率，mi0、ηi0表示共同工作點對應的折合流量以及等熵效率，sfηm和sfηη分別表示折合流量伸縮因子和等熵效率伸縮因子。

4、折合流量-壓比特性曲線平移變換對應的公式為：

m′i＝mi0-acos(sfπθ)+acos(θ)(13)

π′i＝πi0-bsin(sfπθ)+bsin(θ)(14)

其中，m‘i、π’i表示經過平移變換后等轉速曲線上任意一點的折合流量與壓比，mi0、πi0表示共同工作點對應的折合流量和壓比，sfπθ表示平移因子，θ為參數角，0＜θ＜2π，a＝r(1+sfπm)，b＝r(1+sfππ)；

折合流量-等熵效率特性曲線平移變換對應的公式為：

m′i＝mi0-acos(sfηθ)+acos(θ)(15)

η′i＝ηi0-bsin(sfηθ)+bsin(θ)(16)

其中，m‘i、η’i表示經過平移變換后等轉速曲線上任意一點的折合流量與效率，mi0、ηi0表示共同工作點對應的折合流量和壓比，sfηθ表示平移因子，θ為參數角，0＜θ＜2π，a＝r(1+sfηm)，b＝r(1+sfηη)。

5、折合流量-壓比特性曲線旋轉變換對應的公式為：

其中，mi、пi表示經過旋轉變換后等轉速曲線上任意一點的折合流量與壓比，mi0、πi0表示共同工作點對應的折合流量和壓比，表示旋轉因子，m‘i、π’i表示經過平移變換后等轉速曲線上任意一點的折合流量與壓比；

折合流量-等熵效率特性曲線旋轉變換對應的公式為：

其中，mi、hi表示經過旋轉變換后等轉速曲線上任意一點的折合流量與等熵效率，mi0、ηi0表示共同工作點對應的折合流量和壓比，表示旋轉因子，m‘i、η’i表示經過平移變換后等轉速曲線上任意一點的折合流量與等熵效率。

6、變換因子與轉速的多項式關系為：

其中，sfi表示各個變換因子，sfik表示與轉速的多項式關系的多項式系數。

本發明的優勢在于：本發明通過利用穩態運行參數，通過燃氣輪機穩態模型匹配計算方法，確定了不同轉速下的部件共同工作點參數，通過共同工作點與坐標原點實現了部件初始特性的生成，不需要要求有與實際特性近似的初始的參考特性，而適用于各種結構的燃氣輪機部件。

本發明通過對生成的初始部件特性通過伸縮、平移以及旋轉變換，實現了部件實際特性的獲取，相對于現有技術中只能用橢圓方程擬合的方法，本發明中的方法可以針對任意曲線方程生成的初始部件特性實現伸縮、平移以及旋轉變換，因此，可以適用于任意結構的燃氣輪機部件的部件特性獲取，適應性更為廣泛。

附圖說明

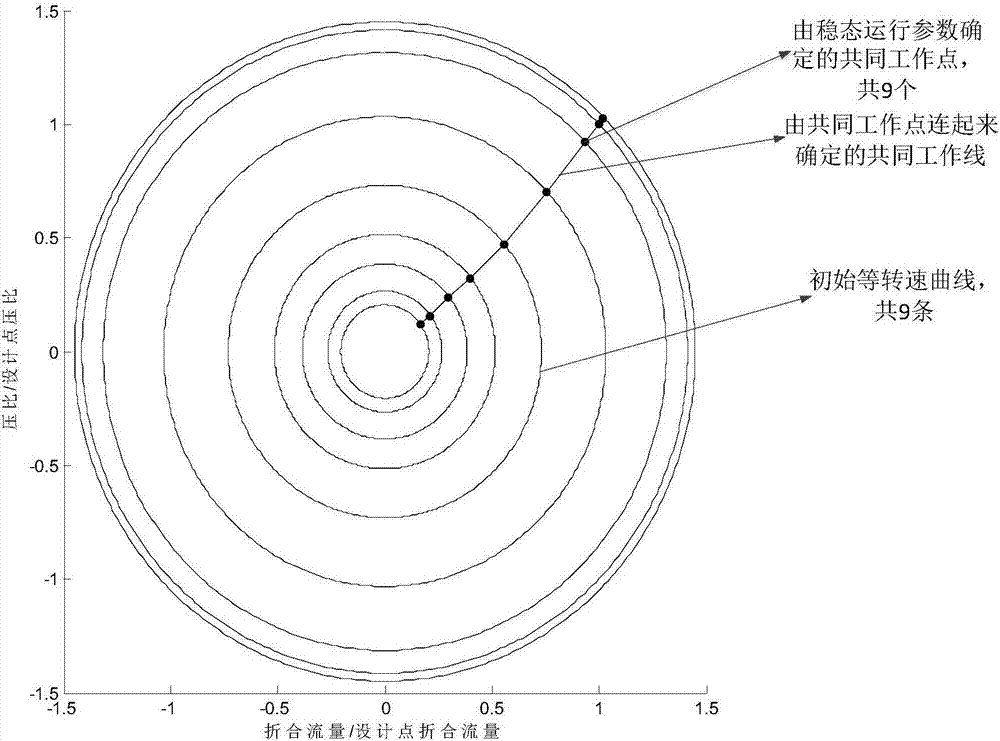
圖1為部件的折合流量-壓比特性的初始特性圖；

圖2為部件的折合流量-等熵效率特性的初始特性圖；

圖3為等轉速曲線從圓曲線變換到橢圓曲線之后的示意圖；

圖4為平移后的橢圓曲線示意圖；

圖5為橢圓曲線繞著共同工作點進行旋轉后的示意圖；

圖6為本發明的流程圖。

具體實施方式

下面結合附圖舉例對本發明做更詳細地描述：

結合圖1-6，本發明的詳細流程如下：

第一步：收集燃氣輪機在不同工況下的穩態運行參數，通過穩態模型計算確定不同穩態工況下的共同工作點參數，包括部件的折合流量、折合轉速、等熵效率以及壓比或者膨脹比，并且把這些參數與設計點參數相除，得到歸一化的參數值。

折合流量的歸一化參數mi如方程(1)所示，壓比的歸一化參數πi如方程(2)所示，折合轉速的歸一化參數ni如方程(3)所示，等熵效率的歸一化參數ηi如方程(4)所示。

mi＝gcor/(gcor)d(1)

πi＝π/πd(2)

ni＝ncor/(ncor)d(3)

ηi＝η/ηd(4)

第二步：根據獲取的不同運行工況下的共同工作點參數，對于部件的折合流量-壓比特性，對于每一個運行工況，以坐標軸原點為圓心，折合流量與壓比值確定的坐標點到圓心的距離為半徑作圓，所作的圓作為該運行工況下對應的等轉速曲線的初始曲線。這樣，有n個運行工況就能作出n個同心圓，所有的同心圓將共同形成部件的折合流量-壓比特性的初始特性圖。對于折合流量與等熵效率特性，對于每一個運行工況，以坐標軸原點為圓心，折合流量與等熵效率確定的坐標點到圓心的距離為半徑作圓，所作的圓作為該運行工況下對應的等轉速曲線的初始曲線。這樣，有n個運行工況就能作出n個同心圓，所有的同心圓將共同形成部件的折合流量-等熵效率特性的初始特性圖。如圖1與圖2所示。

第三步：把部件折合流量-壓比特性的初始特性圖以及部件折合流量-效率特性圖上的每一條等轉速線的表達式都表示成圓的參數方程，這樣等轉速線上的每一點都能夠用參數方程表示，包括之前確定的共同工作點。

折合流量-壓比特性曲線中任意等轉速曲線的參數方程可以表示為如方程(5)和方程(6)所示。

mi＝rcos(θ)(5)

πi＝rsin(θ)(6)

其中，mi、πi表示等轉速線上任意一點的折合流量與壓比，r為共同工作點到原點的距離，θ為參數角，0＜θ＜2π

折合流量-效率特性曲線中任意等轉速曲線的參數方程可以表示為如方程(7)和方程(8)所示。

mi＝rcos(θ)(7)

ni＝rsin(θ)(8)

其中，mi、ηi表示等轉速線上任意一點的折合流量與等熵效率，r為共同工作點到原點的距離，θ為參數角，0＜θ＜2π。

第四步：對于折合流量-壓比初始特性圖，對每一條等轉速線上的每一點都以等轉速線上的共同工作點為中心，引入折合流量伸縮因子以及壓比伸縮因子，對等轉速線進行伸縮變換，使得等轉速曲線從圓曲線變換到橢圓曲線，而對應的共同工作點位置保持不變，如圖3所示。同樣，對于折合流量-等熵效率初始特性圖，對每一條等轉速線上的每一點都以線上的共同工作點為中心，引入折合流量伸縮因子和等熵效率伸縮因子，對等轉速線進行伸縮變換，使得等轉速曲線從圓曲線變換到橢圓曲線，而對應的共同工作點位置保持不變。

折合流量-壓比特性曲線伸縮變換對應的公式為：

m′i＝mi+(mi-mi0)sfπm(9)

π′i＝πi+(πi-πi0)sfππ(10)

其中，m‘i、π’i表示經過伸縮變換后等轉速曲線上任意一點的折合流量與壓比，mi0、πi0表示共同工作點對應的折合流量，壓比，sfπm和sfππ分別表示折合流量伸縮因子和壓比伸縮因子。

折合流量-效率特性曲線伸縮變換對應的公式為：

m′i＝mi+(mi-mi0)sfηm(11)

η′i＝ηi+(ηi-ηi0)sfηη(12)

其中，m‘i、η’i表示經過伸縮變換后等轉速曲線上任意一點的折合流量與效率，mi0、ηi0表示共同工作點對應的折合流量以及等熵效率，sfηm和sfηη分別表示折合流量伸縮因子和等熵效率伸縮因子。

第五步：對于第四步經過伸縮變換的橢圓曲線，引入橢圓曲線的平移因子，使得橢圓曲線圍繞著共同工作點進行平移，而實現的方法是通過改變控制平移的參數角來實現平移，這樣，平移后的橢圓曲線依然經過第一步確定的共同工作點，而橢圓曲線對應的圓心坐標將發生變化，如圖4所示。

折合流量-壓比特性曲線平移變換對應的公式為：

m′i＝mi0-acos(sfπθ)+acos(θ)(13)

π′i＝πi0-bsin(sfπθ)+bsin(θ)(14)

其中，m‘i、π’i表示經過平移變換后等轉速曲線上任意一點的折合流量與壓比，mi0、πi0表示共同工作點對應的折合流量和壓比，sfπθ表示平移因子，θ為參數角，0＜θ＜2π，a＝r(1+sfπm)，b＝r(1+sfππ)。

折合流量-等熵效率特性曲線平移變換對應的公式為：

m′i＝mi0-acos(sfηθ)+acos(θ)(15)

η′i＝ηi0-bsin(sfηθ)+bsin(θ)(16)

其中，m‘i、η’i表示經過平移變換后等轉速曲線上任意一點的折合流量與效率，mi0、ηi0表示共同工作點對應的折合流量和壓比，sfηθ表示平移因子，θ為參數角，0＜θ＜2π，a＝r(1+sfηm)，b＝r(1+sfηη)。

第六步：對于第五步經平移之后的橢圓曲線，引入橢圓曲線的旋轉因子，使橢圓曲線繞著共同工作點進行旋轉，實現的方法也是通過改變控制旋轉的參數角來實現旋轉，旋轉之后的曲線依然經過共同工作點，如圖5所示。

折合流量-壓比特性曲線旋轉變換對應的公式為：

其中，mi、表示經過旋轉變換后等轉速曲線上任意一點的折合流量與壓比，mi0、πi0表示共同工作點對應的折合流量和壓比，表示旋轉因子，m‘i、π’i表示經過平移變換后等轉速曲線上任意一點的折合流量與壓比。

折合流量-等熵效率特性曲線旋轉變換對應的公式為：

其中，mi、hi表示經過旋轉變換后等轉速曲線上任意一點的折合流量與等熵效率，mi0、ηi0表示共同工作點對應的折合流量和壓比，表示旋轉因子，m‘i、η’i表示經過平移變換后等轉速曲線上任意一點的折合流量與等熵效率。

第七步：對于部件的折合流量-壓比特性圖上的每一條等轉速線，都有四個變換因子，即折合流量的伸縮因子，壓比的伸縮因子，曲線的平移因子以及曲線的旋轉因子。而對于折合流量-效率特性圖來說，就包含折合流量伸縮因子，等熵效率伸縮因子，曲線的平移因子以及曲線的旋轉因子。而對于部件特性圖上的每一條等轉速線都能確定4個變換因子，因此，把所有等轉速線對應的變換因子假設為轉速的多項式函數，這樣就能夠獲得任意轉速下對應的變換因子。而上述所提到的折合流量-壓比特性圖對應的4個變換因子以及折合流量-等熵效率對應的4個變換因子，一共8個變換因子認為是確定部件特性的主系數。而每個變換因子與轉速的多項式關系對應的多項式系數稱為子系數。

變換因子與轉速的多項式關系如式(21)所示：

其中，sfi表示各個變換因子，sfik表示與轉速的多項式關系的多項式系數。

第八步：把上述建立的部件特性圖的表達式加入到燃氣輪機仿真模型，與實際運行參數進行匹配，通過實時優化所有子系數的值，使得仿真模型的輸出運行參數與實際的運行參數一致，則確定了子系數的值，通過確定的子系數可以確定的多項式表達式，從而獲得不同等轉速線線的主系數的值，進而生成整個燃氣輪機部件特性，整個發明的流程圖如圖6所示。