一種基于共生相關函數的多孔介質三維建模方法與流程
本發明涉及一種基于二維圖像的多孔介質三維建模方法,尤其涉及一種基于共生相關函數的多孔介質建模方法,屬于圖像處理技術領域。
背景技術:
巖心是多孔介質的一種常見類型,在石油地質領域中,巖心的微觀結構對其宏觀物理特性有著重要的影響。數字巖心是通過計算機圖像處理技術,將巖心的微觀結構以圖像的方式刻畫出來,能夠在孔隙尺寸級別上反映孔隙微觀結構,從而計算巖心聲學、電學特性等性質以及進行滲流模擬過程,分析驅替過程油水變化分布規律等,是巖心分析的有效途徑和方法。利用二維圖像和三維建模方法是獲取巖心三維結構的一種重要方法。
現有的基于二維圖像的多孔介質三維建模方法主要有兩大類:1、將三維重建問題轉為優化問題,利用優化算法進行求解,典型的有模擬退火算法(sa)。2、將二維訓練圖像中出現的模式分布作為一種先驗信息,從而約束三維重建過程,典型的多點地質統計算法(mps)。多點地質統計算法重建結構形態較好,但通常對內存需求較大,同時也穩定性不夠好;模擬退火算法較為靈活,穩定性好,但目前多采用低階統計函數,約束力不夠,從而使得重建結構與真實結構之間有較大差異,因此依然存在一定的局限性。
技術實現要素:
本發明的目的就在于解決模擬退火中采用低階統計導致重建結構與真實結構差異較大的問題,提供了一種基于共生相關函數的多孔介質三維建模方法,提出了能表達圖像紋理特征的共生相關函數作為重建過程的目標函數,并進一步針對該重建算法中速度問題提出了快速更新算法,加快了重建的速度。由于本發明所提出的共生相關函數屬于高階統計函數,當重建結果的共生相關函數與訓練圖像一致時,其低階函數也趨于一致。本發明通過以下技術方案來實現上述目的:
一種基于共生相關函數的多孔介質建模方法,包括以下步驟:
(1)從圖像紋理描述的角度,將二維圖像的紋理分布作為先驗信息,利用共生相關函數提取圖像紋理特征ccf3d,并以此作為重建過程中的約束條件。
(2)隨機初始化三維結構,并計算其三個正交方向的共生相關函數ccf3dx,ccf3dy,ccf3dz,并求得其平均值ccf3d。再計算與二維訓練圖像共生相關函數ccf2d的差值,初始結構的接受概率為0.5。
(3)基于模擬退火算法框架,以共生相關函數ccf2d為目標,利用三維共生相關函數的快速更新算法fastupdate3d,不斷地進行迭代計算,縮小ccf3d與ccf2d之間的差別,并以metropolis準則判斷是否接受該狀態。
(4)迭代達到終止條件,輸出結果。
具體地,所述步驟(1)中,共生相關函數的概念和計算包括:
考慮一個n相多孔介質,我們首先對訓練圖像進行遍歷,獲取到不同相關距離下兩點x1和x2構成的共生相關函數,表示如下:
其中,i,j=1,...,n,nij(r)即表示為這兩個點出現為組合為ij的計數。
為了消除圖像尺寸對共生相關函數的影響,需要進一步進行歸一化,歸一化之后表示如下:
其中,
對于統計均質、各項同性的多孔介質而言,兩點之間的關系之和它們的距離相關,因此ccf可以進一步表示為:
ccf(x1,x2)=ccf(r),(3)
其中,r=|x1-x2|,即兩點之間的距離。
對于給定的訓練圖像(如圖1所示),根據共生相關函數的定義,掃描圖像獲取其共生相關函數。根據兩點構成的不同模式,將其分別記錄到矩陣的對應位置,掃描完成,并進行歸一化,消除圖像尺寸對其的影響,得到的最終的歸一化結果作為約束函數。
所述步驟(2)中,隨機初始化三維結構和計算ccf3d包括:
根據二維訓練圖像的孔隙度
其中p=0.5,來設置好初始溫度t0。再設置其他的重建參數:降溫系數λ,迭代步長step等。
所述步驟(3)中,基于模擬退火算法框架的重建過程包括:
a.數學模型的建立
即對問題形式的描述,由解空間、目標函數和初始解三部分組成。解空間是問題的所有可能解的集合,限定了初始解選取和新解產生的范圍。目標函數是對優化目標的數學描述。初始解是算法開始迭代的起點。
b.狀態產生函數
通常,狀態產生函數的關鍵是產生候選解的方式和候選解產生的概率分布。候選解的產生方式與問題的性質有關,通常在當前狀態的鄰域結構內按照一定的概率產生,而鄰域的概念及概率產生方式有很多,其中概率分布可以是均勻分布、正態分布、泊松分布、柯西分布等,我們采用的是均勻分布和metropolis接受準則,即:
c.初始溫度和溫度更新函數
一般來說,初始溫度越高,獲得能量較低的解的概率越大,但需要的時間也越長。因此,初始溫度的確定應折衷考慮優化效果和優化效率。溫度更新函數給出了溫度的下降方式。單純加快溫度下降速度并不能保證算法以較快的速度達到全局最優,溫度下降的速度必須與狀態產生函數相匹配,我們采用的是指數形式tk+1=λtk。初始溫度和溫度更新函數構成冷卻進度表(coolingschedule),控制模擬退火算法的進程,使模擬退火算法逼近漸進收斂性,在有限的迭代次數內返回一個近似的最優解。
在每一次交換兩個不同相的點之后,整個三維結構只有沿這兩點的三個正交方向的ccf3dx,ccf3dy,ccf3dz發生改變,因此我們只需要利用快速更新算法fastupdate3d去重新計算變化了的ccf3dx,ccf3dy,ccf3dz,從而快速得到新的三維結構的共生相關函數ccf3d,加快了重建過程。
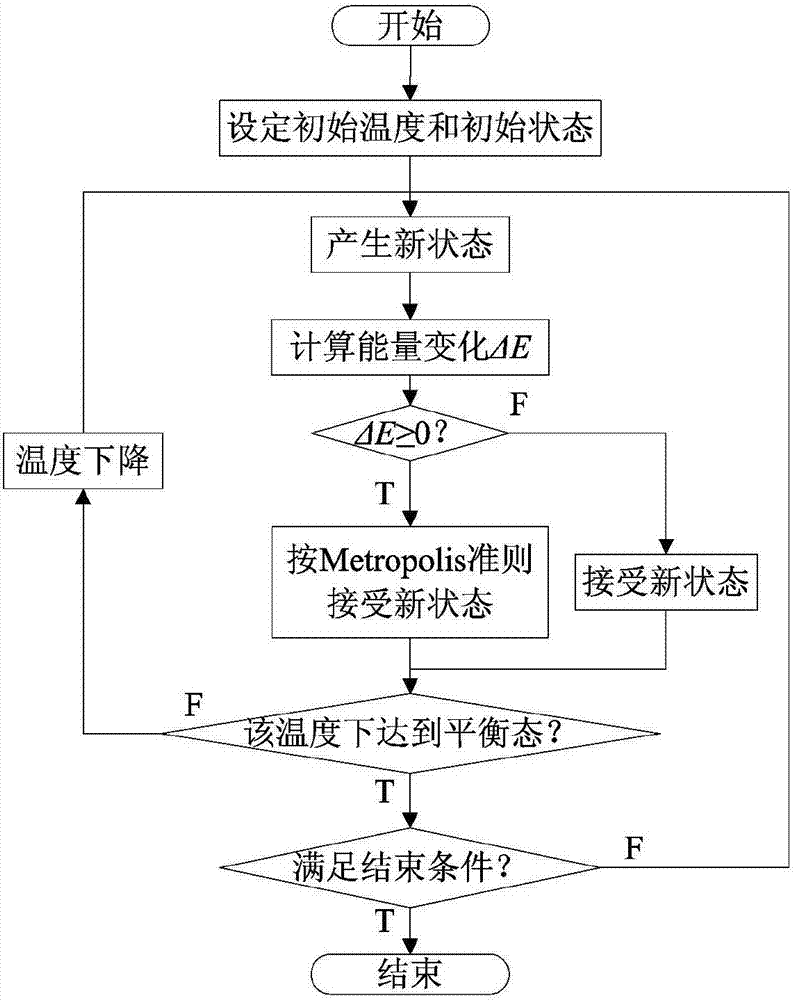
模擬退火算法的流程如圖2所示。
所述步驟(4)中,迭代達到終止條件包括:
通常可以將一個可以接受的誤差δe,溫度降到某個很小的值tmin或者拒絕次數達到一個最大值n作為終止條件。
本發明受國家自然科學基金“巖石微觀非均質結構三維圖像重建及分辨率提升技術研究(61372174)”資助。
附圖說明
圖1二維訓練圖像的示意圖
圖2模擬退火流程圖
圖3兩點概率,線性路徑,兩點簇函數示意
圖4例子中所用二維訓練圖像
圖5巖心圖像重建對比圖
圖6統計特征曲線對比
具體實施方式
下面結合附圖對本發明作進一步說明:
(1)掃描二維訓練圖像,獲取其共生相關函數。根據兩點構成的不同模式,將其分別記錄到對應位置,掃描完成,并進行歸一化,消除圖像尺寸對其的影響。
(2)按照孔隙度初始化目標三維結構,并計算其對應的共生相關函數。三維目標結構的計算方式與二維圖像有所差異,需要分別計算三個切面方向相關函數,再進行歸一化和平均,初始結構的接受概率為0.5,并設置好初始溫度。
(3)根據模擬退火的策略,不斷的交換兩個不同相的點,并計算相應地共生相關函數及與目標共生相關函數的差值,按照一定準則判斷是否接受新狀態,不斷迭代尋找最優。
(4)迭代達到終止條件,輸出結果。
具體地,所述步驟(1)中,圖4為兩相多孔介質的二維訓練圖像。我們首先對訓練圖像進行遍歷,基于各項同相的假設,我們獲取到不同相關距離下的共生相關函數,表示如下:
其中,r為兩個點相距的距離,i,j=0,1.即兩個點為0,1的不同取值,nij(r)即表示為這兩個點出現為組合為ij的計數。
對其進行歸一化得到
其中,
所述步驟(2)中,根據孔隙度對三維結構進行隨機初始化,并計算對應的共生相關函數。根據二維訓練圖像的孔隙度
所述步驟(3)中,基于模擬退火框架的重建算法主要包括:
利用兩點不斷交換,產生新的解,根據概率接受的準則判斷是否接受該狀態,不斷的進行迭代,最終達到與目標的共生相關函數的差值最小。
需要注意的是,在每一次點交換之后,都需要去計算其對應的共生相關函數以及和目標之間的差值,這個過程有成千上萬次,因此設計了快速更新算法,從而高效快速第更新共生相關函數,加快重建速度。
所述步驟(4)中,重建過程達到終止條件,結束整個過程。終止條件通常有幾種類型,比如可以設置重建結構與目標結構之間的差值小于一定閾值,或者溫度下降到某個很小的值等。一旦達到終止條件,則退出循環,輸出重建結果。我們設置的終止條件有以幾個,達到任何一個都終止重建過程:
(a)三維重建結構與二維訓練圖像的共生相關函數差值小于10-5.
(b)溫度下降到初始溫度的10-37。
(c)拒絕次數大于200000次。
通常來講,由于(a)和(c)的條件相對嚴格,不容易滿足,因此終止條件(b)通常最先達到。
重建完成之后,為了對重建結果進行驗證,我們采用了常用的兩點概率函數s2,線性路徑函數l以及兩點簇函數c2。標準兩點概率函數s2重建作為實驗對比。兩點相關函數s2定義二維圖像或三維結構任意兩點同時屬于孔隙相的概率。線性路徑函數l定義為整個線段整個屬于孔隙相的概率。這兩者都是低階的統計,兩點簇函數c2定義為任意兩點同時屬于同一個簇的概率,是高階的統計特性。三種函數的定義如圖3所示。下面對重建結果進行驗證:
圖4為巖心二維訓練圖像,圖5巖心圖像重建對比圖,其中(a)為真實ct結構,(b)(c)分別為我們提出的算法ccf2和s2的重建結果。圖6為三種函數的統計特征曲線對比。
可以看出,相比s2重建,我們的算法不僅是直觀上的形態還是統計特征,都和目標結構相似,s2重建的線性路徑比較接近,但是兩點簇函數偏大。同時s2重建耗時約1.8小時,我們算法耗時為1.9小時,后者在時間上并沒有明顯提升。根據以上的驗證結果可知,提出的重建算法的具有較好的準確性和較低的計算成本。
上述實施例只是本發明的優選實施案例,并不是對本發明所述技術方案的限制,只要是不經過創造性勞動即可在上述實施案例的基礎上實現的技術方案,均應視為落入本發明內容的保護范圍內。
- 還沒有人留言評論。精彩留言會獲得點贊!