一種基于量子混沌映射和分數域變換的圖像加密方法與流程
本發明涉及混沌通訊保密領域,特別涉及一種基于量子混沌映射和分數域變換的圖像加密方法。
背景技術:
隨著網絡通信和計算機技術的快速發展,圖像作為信息的一種重要載體,由于信息量豐富,直觀性強等特點,被廣泛應用于各個領域。圖像傳遞的安全性和保密技術引起了人們的密切關注。探索高效,安全的圖像加密方法已成為廣大學者的研究的一門重要課題。
混沌系統由于具有初值敏感性,偽隨機性等優良的密碼學特性。基于此,學者們紛紛提出一些混沌圖像加密方法。常用的圖像加密的經典思想主要有以下3種:基于圖像像素空間位置置亂,基于圖像灰度的變換,基于這兩者的結合。其中主要研究方向為從低維到高維,從單一混沌系統到多維混沌系統的轉變。gao等人提出采用像素置亂和像素變換相結合機制的加密方法,盡管構造簡單,但是密鑰與明文無關,導致無法有效有效抵制選擇明文攻擊。王等人提出了一種超混沌圖像加密方法,通過密文反饋機制控制方法中的密鑰流,使得加密所需要參數與明文密切相關。但由于周期短,復雜度低,容易被破解。當前大多數混沌加密方法都是自然混沌系統,嚴格意義上說沒有達到密碼學所要求的保密性和安全性,即容易被攻破。基于此,在變換域中進行圖像加密算法成為近年來的研究方向。unnikrishnan等人在2000年首次將分數階fourier變換用于圖像加密。由于分數階fourier可加性和變換階數可以為圖像加密方法提供更多的自由度,已經逐漸成為圖像加密中的重要研究熱點之一。綜上,人們又考慮到混沌系統自身有許多優良特性,王等人提出將混沌系統和分數階fourier變換結合在一塊的圖像加密方法。實驗結果和仿真表明該方法比之前的方法安全性要好。隨著信息技術的快速發展,量子圖像也進入了人們的視野,學者們開始研究更加高效和安全的量子圖像加密技術。在2012年,akhshania等人基于量子logistic映射提出了一個圖像加密方案,該研究為量子混沌映射應用于密碼學領域指明了方向。與傳統的加密技術相比,量子混沌映射具有天然的并行性,大容量和難以破解等優點。基于此,提出一種基于量子混沌映射和分數域變換的圖像加密方法。
技術實現要素:
本發明的目的在于克服現有技術的缺點與不足,提供一種基于量子混沌映射和分數域變換的圖像加密方法,克服了傳統分數階fourier變換后直方圖不夠平滑的缺點,本發明方法通過引入量子混沌映射,有效避免了傳統混沌系統偽隨機性差,計算復雜度高,控制參數少等問題,同時將混沌系統和分數階fourier變換結合起來,實現了介于空間域和頻域的分數域置亂,置亂效果好,避免了輕易能夠破解的問題。安全性得到了提高。
本發明的目的通過下述技術方案實現:一種基于量子混沌映射和分數域變換的圖像加密方法,包括以下步驟:
步驟一:打開原始的lena(256×256)灰度bmp圖像,按照從左往右的順序依次讀取圖像中各點像素值,得到原始圖像的像素矩陣q。因其圖像高度和寬度相等,這里假設高度和寬度用m表示.
步驟二:利用henon映射產生兩個m×m混沌序列分別為x={xk|k=0,1,2,3,…,m×m},y={yk|k=0,1,2,3,…,m×m},henon映射的動力學方程如下式(1):
輸入a,b,x0,y0,其中a和b為混沌系統控制參數,x0,y0為初始值,將a,b,x0,和y0作為加密密鑰,然后從x和y中第i+1項開始,截取其中t項得到序列c={ck|k=i+1,i+2,…,i+t},即{ci+1,ci+2,ci+3,…,ci+t},d={dk|k=i+1,i+2,…,i+t},即{di+1,di+2,di+3,…,di+t},然后取整數部分作為新的序列值,再分別各自重新組成和原始圖像同樣大小的矩陣cx和dy。
步驟三:將步驟二的c,d序列進行排序得到{c(i+1)′,c(i+2)′,c(i+3)′,…,c(i+t)′},{d(i+1)′,d(i+2)′,d(i+3)′,…,d(i+t)′},然后計算出此序列在原x,y序列中的位置信息,記錄坐標位置索引序列c′,d′,將原始圖素像素矩陣q各元素按c′索引序列的從左往右順序賦值為1~t的自然數,序列位不夠的元素所在位置為奇數行置1,偶數行置t,得到置亂行矩陣px,同理,將原始圖像各元素按d′索引序列的順序賦值為1~t的自然數,序列位不夠的元素所在為奇數列置1,偶數列置t,得到置亂列矩陣py.
步驟四:將原始圖像像素矩陣q和步驟得到的cx和dy矩陣,按位相乘處理,即通過式o=q×cx×dy,處理后得到圖像矩陣o。
步驟五:將圖像矩陣o乘以行置亂矩陣px,得到r,將r矩陣看做一個行向量r′=(u1,u2,u3,…um)進行x方向的a階傅里葉變換,得到復數矩陣j,然后將j與置亂列矩陣py相乘,得到復數矩陣i。將i矩陣看做一個列向量i′(v1,v2,v3,…vm)進行y方向的b階傅里葉變換,得到加密復數矩陣。并通過式(2)求出幅度譜。
|f(m,n)|=[r2(m,n)+i2(m,n)]1/2(2)
r(m,n)和i(m,n)分別為f(m,n)實數部分和虛數部分。
步驟六:將步驟五得到的加密復數矩陣通過下式(3)~(4)逆變換從頻域轉換成空間域。
其中f(m,n)為圖像的灰度分布函數,其里面的m,n為圖像設定的空間域,f(m,n)為圖像的頻率分布函數,里面的u,v為圖像設定的頻率域。|f(m,n)|和
然后將得到的矩陣以一維數組的形式讀取得到序列f={fk|k=0,1,2,3,…,m×m},接著利用量子logistic映射下式(5)產生序列gx,gy,gz。量子logistic映射動力學方程如下式。
式中,控制參數r∈(3.74,4.00),耗散參數β≥3.5,x′n,y′n,z′n,是該混沌系統的狀態值,且通常情況下都為復數,
步驟七:將gx異或gy異或gz,得到序列h={hk|k=0,1,2,3,…,m×m},最后利用混沌bernoulli映射方程(式6)迭代m次產生序列l={lk|k=0,1,2,3,…,m×m},接著將hk,lk和步驟六的得到fk序列通過下式(7)進行預處理,將其都轉化為0至255之間的整數。
bernoulli映射方程式如下:
式中,c為bernoulli映射參數,c∈(1.4,2)時,bernoulli移位映射進入混沌狀態。
令得到最終密文序列為s={sk|k=0,1,2,3,…,m×m},s序列通過以下線性公式(8)遞推得到。
sk+1=mod(sk+lk+fk,256)(8)
步驟八:將步驟七的密文序列s重新塑造成二維矩陣,得到最終的加密密文圖像。
本發明相對于現有技術具有如下的優點及效果:基于傳統的自然混沌系統安全性不高,本發明方法選取隨機性非常好的量子混沌中映射對圖像像素進行修改擴散,因其量子logistic混沌映射末尾有一個擾動修正量,使每次迭代更新不會丟失,產生的序列非周期性比傳統logistic映射要好,偽隨機性更強。同時結合分數階傅利葉變換,實現了介于頻域和空間域之間的分數域置亂。使得加密復雜度大大加強,不容易被攻擊破解。更能達到良好的加密效果。
附圖說明
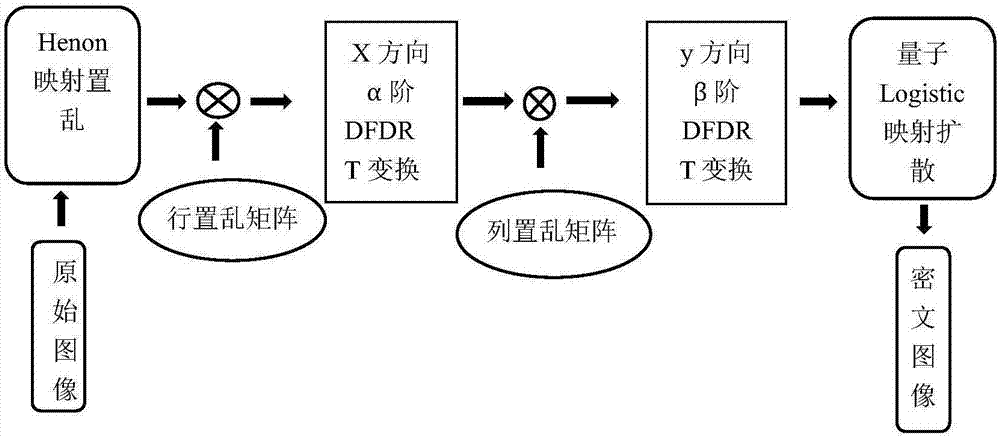
圖1是本發明方法加密流程圖;
圖2是henon映射分岔圖;
圖3中:圖(a)是原始圖像(b)是置亂后的圖像(c)是x方向dfrft加密幅值圖(d)是y方向dfrft加密幅值圖(e)是量子映射擴散最終加密圖像。
具體實施方式
下面結合實施例及附圖對本發明作進一步詳細的描述,但本發明的實施方式不限于此。
實施例
本發明方法選取經典lena(256×256)灰度圖像(如圖3a)為實驗測試仿真對象。圖像的加密方法是在matlab2016a環境下進行,加密工作流程圖如圖1,實驗密鑰數據如下:henon映射初始值x0=0.32658698,y0=0.26853267,控制參數a=1.4,b=0.3,量子logistic混沌映射初始值
x′0=0.46983651,y′0=0.002659835123,z′0=0.002658789456,r=3.9,β=3.5,bernoulli映射參數c=1.4.
步驟一:打開原始的lena(256×256)灰度bmp圖像,按照從左往右的順序依次讀取圖像中各點像素值,得到原始圖像的像素矩陣q。因其圖像高度和寬度相等,這里假設高度和寬度用m表示.
步驟二:利用henon映射產生兩個m×m混沌序列分別為x={xk|k=0,1,2,3,…,m×m},y={yk|k=0,1,2,3,…,m×m},henon映射的動力學方程如下式(1):
輸入a,b,x0,y0,其中a和b為混沌系統控制參數,x0,y0為初始值,將a,b,x0,和y0作為加密密鑰,然后從x和y中第i+1項開始,截取其中t項得到序列c={ck|k=i+1,i+2,…,i+t},即{ci+1,ci+2,ci+3,…,ci+t},d={dk|k=i+1,i+2,…,i+t},即{di+1,di+2,di+3,…,di+t}然后取整數部分作為新的序列值,再分別各自重新組成和原始圖像同樣大小的矩陣cx和dy。
步驟三:將步驟二的c,d序列進行排序得到{c(i+1)′,c(i+2)′,c(i+3)′,…,c(i+t)′},{d(i+1)′,d(i+2)′,d(i+3)′,…,d(i+t)′},然后計算出此序列在原x,y序列中的位置信息,記錄坐標位置索引序列c′,d′,將原始圖素像素矩陣q各元素按c′索引序列的從左往右順序賦值為1~t的自然數,序列位不夠的元素所在位置為奇數行置1,偶數行置t,得到置亂行矩陣px,同理,將原始圖像各元素按d′索引序列的順序賦值為1~t的自然數,序列位不夠的元素所在為奇數列置1,偶數列置t,得到置亂列矩陣py.
步驟四:將原始圖像像素矩陣q和步驟得到的cx和dy矩陣,按位相乘處理,即通過式o=q×cx×dy,處理后得到圖像矩陣o。
步驟五:將圖像矩陣o乘以行置亂矩陣px,得到r,將r矩陣看做一個行向量r′=(u1,u2,u3,…um)進行x方向的a階傅里葉變換,得到復數矩陣j,然后將j與置亂列矩陣py相乘,得到復數矩陣i。將i矩陣看做一個列向量i′(v1,v2,v3,…vm)進行y方向的b階傅里葉變換,得到加密復數矩陣。并通過式(2)求出幅度譜和相位譜。
|f(m,n)|=[r2(m,n)+i2(m,n)]1/2(2)
r(m,n)和i(m,n)分別為f(m,n)實數部分和虛數部分。
步驟六:將步驟五得到的加密復數矩陣通過下式(3)~(4)逆變換從頻域轉換成空間域,然后將得到的矩陣以一維數組的形式讀取得到序列f={fk|k=0,1,2,3,…,m×m},接著把密鑰x′0,y′0,z′0,r,β,作為量子logistic映射(5)的初始值產生序列gx,gy,gz。
其中f(m,n)為圖像的灰度分布函數,其里面的m,n為圖像設定的空間域,f(m,n)為圖像的頻率分布函數,里面的u,v為圖像設定的頻率域。|f(m,n)|和
量子logistic映射動力學方程如下式(5)。
式中,控制參數r∈(3.74,4.00),耗散參數β≥3.5,x′n,y′n,z′n,是該混沌系統的狀態值,且通常情況下都為復數,
步驟七:將gx異或gy異或gz,得到序列h={hk|k=0,1,2,3,…,m×m},最后利用混沌bernoulli映射迭代m次(式6)產生序列l={lk|k=0,1,2,3,…,m×m},接著將hk,lk和步驟六的得到fk序列通過下式(7)進行預處理,將其都轉化為0至255之間的整數。
bernoulli映射方程式如下:
式中,c為bernoulli映射參數,c∈(1.4,2)時,bernoulli移位映射進入混沌狀態。
令得到最終密文序列為s={sk|k=0,1,2,3,…,m×m},s序列通過線性公式遞推得到(式8)。
sk+1=mod(sk+lk+fk,256)(8)
步驟八:將步驟七的密文序列s重新塑造成二維矩陣,得到最終的加密密文圖像。
上述實施例為本發明較佳的實施方式,但本發明的實施方式并不受上述實施例的限制,其他的任何未背離本發明的精神實質與原理下所作的改變、修飾、替代、組合、簡化,均應為等效的置換方式,都包含在本發明的保護范圍之內。
- 還沒有人留言評論。精彩留言會獲得點贊!