無級縮放超分辨率圖像的重建方法與流程
本發明屬于圖像重建技術領域,具體涉及一種無級縮放超分辨率圖像的重建方法。
背景技術:
當前,圖像分辨率會受到成像系統、拍攝環境等因素的影響,得到的圖像分辨率往往無法滿足人們的需求。然而,目前光學成像系統及其探測器又受限于技術水平及加工復雜度,無法從硬件角度改善系統成像質量。因此,圖像超分辨率重建技術的出現,打破了圖像分辨率的限制。通過軟件處理的方式從一幅或者多幅退化的低分辨率圖像中,計算出一幅高分辨率圖像,獲得更加豐富的細節信息。目前超分辨率重建技術廣泛應用于圖像處理及光學成像領域,得到了人們的重視。
目前,基于學習的稀疏表示圖像超分辨率重建算法可以有效提高圖像的分辨率,并且對圖像進行放大倍率為3的尺度放大。然而,在某些特定情況下,經過該方法得到的高分辨率圖像達不到所需的尺度要求。
因此,如何提供一種圖像重建方法使得獲得的超分辨率重建圖像可以進行任意尺度的變換,以達到相關工業要求變得至關重要。
技術實現要素:
為了解決現有技術中存在的上述問題,本發明提供了一種無級縮放超分辨率圖像的重建方法,包括如下步驟:
步驟1,對高分辨率樣本圖像按照退化模型進行模糊處理和n倍下采樣,獲得低分辨率樣本圖像;
步驟2,采用k-svd方法,利用所述低分辨率樣本圖像進行字典訓練,得到高分辨字典和低分辨率字典;
步驟3,對待重建的低分辨率圖像進行預處理得到若干個低分辨率圖像塊;
步驟4,利用所述低分辨率樣本圖像計算固定閾值;
步驟5,判斷每一個所述低分辨率圖像塊的像素值是否小于所述固定閾值;若是,則判定該所述低分辨率圖像塊為低信息量圖像塊;若否,則判定該所述低分辨率圖像塊為高信息量圖像塊;
步驟6,將所述高信息量圖像塊采用基于字典學習與稀疏表示算法重建得到高信息量重建子區域;
步驟7,將所述低信息量圖像塊采用插值算法進行重建得到低信息量重建子區域;
步驟8,將所述高信息量子區域與所述低信息量重建子區域進行圖像拼接得到超分辨率重建圖像;
步驟9,采用插值算法將所述超分辨率重建圖像進行m倍插值得到n*m(n=2,3,4;m>0)倍的超分辨率重建圖像。
在本發明的一個實施例中,所述步驟2包括如下步驟:
(21)通過特征提取方法提取所述低分辨率樣本圖像的圖像特征,得到空間目標的高分辨率特征信息和低分辨率特征信息。
(22)利用所述k-svd方法,對所述高分辨率特征信息和所述低分辨率特征信息進行聯合訓練,得到所述高分辨率字典和所述低分辨率字典。
在本發明的一個實施例中,所述步驟(22)包括如下步驟:
(221)利用稀疏k-svd方法訓練低分辨率字典;
(222)計算高分辨率字典。
在本發明的一個實施例中,所述步驟3包括如下步驟:
(31)對所述待重建的低分辨率圖像去噪聲得到第一圖像;
(32)將所述第一圖像去模糊得到第二圖像;
(33)將所述第二圖像按照固定長寬進行分割、保存處理,形成所述低分辨率圖像塊。
在本發明的一個實施例中,所述步驟4包括如下步驟:
(41)將所述低分辨率樣本圖像進行區塊分割得到低分辨率樣本圖像塊;
(42)利用邊緣提取算法提取所述低分辨率樣本圖像塊的邊緣信息,統計各所述低分辨率樣本圖像塊的像素值和所有所述低分辨率樣本圖像塊的像素值分布情況;
(43)根據所述各低分辨率樣本圖像塊的像素值和所有所述低分辨率樣本圖像塊的像素值分布情況選取x(x>1)個候選閾值;
(44)對每個所述候選閾值利用基于學習的稀疏表示圖像超分辨率重建算法進行計算形成多個高分辨率候選圖像;
(45)根據所述基于學習的稀疏表示圖像超分辨率重建算法的運算時間及對應形成的所述高分辨率候選圖像的分辨率,從x個候選閾值中選擇所述信息量閾值。
在本發明的一個實施例中,所述邊緣提取算法為canny算子邊緣檢測算法。
在本發明的一個實施例中,所述步驟6包括如下步驟:
(61)針對所述高信息量圖像塊進行圖像濾波處理,并進行高頻特征提取獲得高頻信息;
(62)利用所述高頻信息對所述高信息量圖像塊進行kpca降維,實現高維數據壓縮;
(63)采用omp算法對降維壓縮后的數據進行重建得到所述高信息量重建子區域。
在本發明的一個實施例中,所述圖像濾波操作采用二維濾波算子濾波器組,所述濾波器組為f={f1,f2,f3,f4},其中,
f1=[1,-1],f2=f1t
f3=log,f3=f3t
t為矩陣轉置操作,log為5×5的二維濾波算子。
在本發明的一個實施例中,所述步驟(63)包括如下步驟:
(631)根據所述omp算法計算稀疏表示系數β,其中,
其中,y為降維解壓后的數據,t0為給定的稀疏度,βi為矩陣β中的子元素;
(632)將所述稀疏表示系數β與所述高分辨率字典相乘,得到所述高信息量重建子區域。
在本發明的一個實施例中,所述插值算法為雙三次插值算法。
本發明實施例具有如下有益效果,
1、本發明實施例提出建立圖像庫訓練字典的方法,將圖像集離線訓練字典庫,得到高分辨率圖像與低分辨率圖像的映射關系,優化圖像重建步驟,有效減少方法運行時間,具有自適應性和高效性。
2、本發明獲得的超分辨率重建圖像可以進行任意大小的尺度變換。在工程應用中可以滿足不同的情況下的需求,有較好的適用性。
3、本發明中方法中的閾值是基于大量對比試驗后進行優化固定,在處過程中不需要進行改變,在不影響圖像重建效果的情況下,有效的提高了圖像重建效率。
4、依據超分辨率重建后的圖像再進行縮放,由于算法重構了高頻信息,對于縮放效果會更好。
附圖說明
圖1為本發明實施例提供的一種無級縮放超分辨率圖像的重建方法流程示意圖;
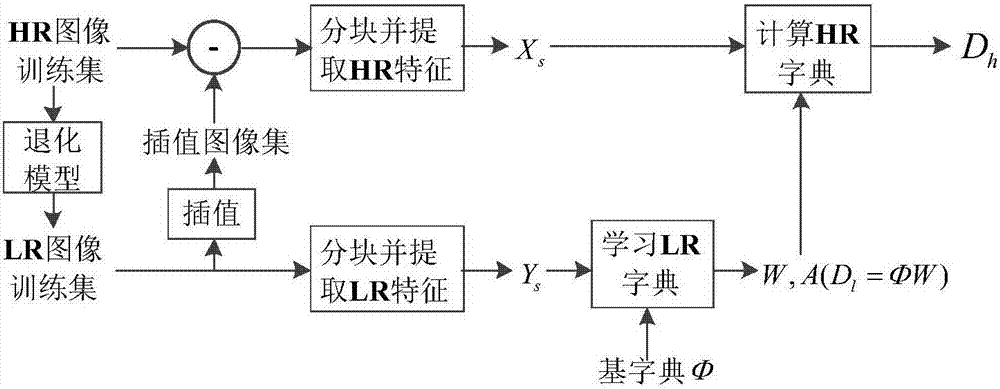
圖2為本發明實施例提供的一種字典訓練原理示意圖;
圖3為本發明實施例提供的一種無級縮放超分辨率圖像的重建方法原理示意圖。
具體實施方式
下面結合具體實施例對本發明做進一步詳細的描述,但本發明的實施方式不限于此。
實施例一
請參見圖1、圖2和圖3,圖1為本發明實施例提供的一種無級縮放超分辨率圖像的重建方法流程示意圖;圖2為本發明實施例提供的一種字典訓練原理示意圖;圖3為本發明實施例提供的一種無級縮放超分辨率圖像的重建方法原理示意圖。該無級縮放超分辨率圖像的重建方法,包括如下步驟:
步驟1,對高分辨率樣本圖像按照退化模型進行模糊處理和n倍下采樣,獲得低分辨率樣本圖像;
步驟2,采用k-svd方法,利用所述低分辨率樣本圖像進行字典訓練,得到高分辨字典和低分辨率字典;
其中,步驟1和步驟2建立圖像庫訓練字典的方法,將圖像集離線訓練字典庫,得到高分辨率圖像與低分辨率圖像的映射關系,優化圖像重建步驟,有效減少方法運行時間,具有自適應性和高效性。
步驟3,對待重建的低分辨率圖像進行預處理得到若干個低分辨率圖像塊;
步驟4,利用所述低分辨率樣本圖像計算固定閾值;
步驟5,判斷每一個所述低分辨率圖像塊的像素值是否小于所述固定閾值;若是,則判定該所述低分辨率圖像塊為低信息量圖像塊;若否,則判定該所述低分辨率圖像塊為高信息量圖像塊;
其中,步驟5在保證重建質量的同時,顯著提高了重建速度,適合對時間性能要求較高的應用。
步驟6,將所述高信息量圖像塊采用基于字典學習與稀疏表示算法重建得到高信息量重建子區域;
其中,基于學習的稀疏表示重建方法避免了近鄰數目的人為選擇,重建效果較好。
步驟7,將所述低信息量圖像塊采用插值算法進行重建得到低信息量重建子區域;
步驟8,將所述高信息量子區域與所述低信息量重建子區域進行圖像拼接得到超分辨率重建圖像;
步驟9,采用插值算法將所述超分辨率重建圖像進行m倍插值得到n*m(n=2,3,4;m>0)倍的超分辨率重建圖像。
具體地,所述步驟2包括如下步驟:
(21)通過特征提取方法提取所述低分辨率樣本圖像的圖像特征,得到空間目標的高分辨率特征信息和低分辨率特征信息。
(22)利用所述k-svd方法,對所述高分辨率特征信息和所述低分辨率特征信息進行聯合訓練,得到所述高分辨率字典和所述低分辨率字典。
其中,所述步驟(22)包括如下步驟:
(221)利用稀疏k-svd方法訓練低分辨率字典;
(222)計算高分辨率字典。
具體地,所述步驟3包括如下步驟:
(31)對所述待重建的低分辨率圖像去噪聲得到第一圖像;
(32)將所述第一圖像去模糊得到第二圖像;
(33)將所述第二圖像按照固定長寬進行分割、保存處理,形成所述低分辨率圖像塊。
具體地,所述步驟4包括如下步驟:
(41)將所述低分辨率樣本圖像進行區塊分割得到低分辨率樣本圖像塊;
(42)利用邊緣提取算法提取所述低分辨率樣本圖像塊的邊緣信息,統計各所述低分辨率樣本圖像塊的像素值和所有所述低分辨率樣本圖像塊的像素值分布情況;
(43)根據所述各低分辨率樣本圖像塊的像素值和所有所述低分辨率樣本圖像塊的像素值分布情況選取x(x>1)個候選閾值;
(44)對每個所述候選閾值利用基于學習的稀疏表示圖像超分辨率重建算法進行計算形成多個高分辨率候選圖像;
(45)根據所述基于學習的稀疏表示圖像超分辨率重建算法的運算時間及對應形成的所述高分辨率候選圖像的分辨率,從x個候選閾值中選擇所述信息量閾值。
優選地,所述邊緣提取算法為canny算子邊緣檢測算法;
再者,所述步驟6包括如下步驟:
(61)針對所述高信息量圖像塊進行圖像濾波處理,并進行高頻特征提取獲得高頻信息;
(62)利用所述高頻信息對所述高信息量圖像塊進行kpca降維,實現高維數據壓縮;
(63)采用omp算法對降維壓縮后的數據進行重建得到所述高信息量重建子區域。
進一步的,所述圖像濾波操作采用二維濾波算子濾波器組,所述濾波器組為f={f1,f2,f3,f4},其中,
f1=[1,-1],f2=f1t
f3=log,f3=f3t
t為矩陣轉置操作,log為5×5的二維濾波算子。
進一步的,所述步驟(63)包括如下步驟:
(631)根據所述omp算法計算稀疏表示系數β,其中,
其中,y為降維解壓后的數據,t0為給定的稀疏度,βi為矩陣β中的子元素。
(632)將所述稀疏表示系數β與所述高分辨率字典相乘,得到所述高信息量重建子區域。
優選地,所述的插值算法為雙三次插值算法。還可以采用例如線性插值、最鄰近元法、雙線性內插法等。
本實施例具有如下優點:
1、本發明實施例提出建立圖像庫訓練字典的方法,將圖像集離線訓練字典庫,得到高分辨率圖像與低分辨率圖像的映射關系,優化圖像重建步驟,有效減少方法運行時間,具有自適應性和高效性。
2、本發明獲得的超分辨率重建圖像可以進行任意大小的尺度變換。在工程應用中可以滿足不同的情況下的需求,有較好的適用性。
3、本發明中方法中的閾值是基于大量對比試驗后進行優化固定,在處過程中不需要進行改變,在不影響圖像重建效果的情況下,有效的提高了圖像重建效率。
實施例二
在上述實施例一的基礎上,本實施例提供另一種無級縮放超分辨率圖像的重建方法,包含字典訓練過程、圖像重建過程、尺度變化過程三個處理步驟。具體包括如下步驟:
s1:字典重建過程。
s11:利用大量高分辨率樣本圖像,將高分辨率圖像按照修正后的退化模型進行模糊和n倍下采樣,得到相應的低分辨率樣本圖像。
s12:對步驟1獲得的低分辨率樣本圖像通過特征提取方法提取圖像特征,得到空間目標的高低分辨率特征信息即xs和ys。
s13:利用k-svd方法,對高低分辨率特征信息進行聯合訓練,得到高低分辨率字典。
s13a:訓練低分辨率字典。基字典φ選擇過完備dct字典,利用稀疏k-svd方法求解:
則低分辨率字典dl=φw,w是一個原子表示矩陣。與解析字典模型相比,雙稀疏字典模型通過對w的修改提供了自適應性。
s13b:計算高分辨率字典。假設高分辨率—低分辨率圖像塊在高分辨率—低分辨率字典對下具有相同的稀疏表示系數a,則可以通過最小化以下公式中的逼近誤差來計算高分辨率字典dh:
使用偽逆求解:
dh=xsa+=xsat(aat)-1(3)
其中,上標“+”表示偽逆。
s2圖像重建過程。
s21:對待重建的低分辨率圖像進行預處理,其中主要包括圖像去噪、圖像去模糊和樣本分塊操作。其處理步驟為:
s21a:對待重建的低分辨率圖像去噪聲;
s21b:對步驟s21a得到的圖像去模糊;
s21c:對步驟s21b得到的圖像進行區塊劃分,將整幅圖像按照固定長寬進行分割、保存;
s22:利用步驟s11中獲得的低分辨率樣本圖像計算固定閾值,具體處理步驟如下:
s22a:將步驟s11中得到的大量低分辨率樣本圖像進行區塊分割獲得圖像塊,圖像塊的長寬同步驟s21c;
s22b:利用邊緣提取算法提取圖像塊邊緣信息,統計各圖像塊的信息量及所有圖像塊的信息量分布情況;
s22c:選取圖像塊中信息量最高的,獲取該圖像塊的像素值為f1,取f=f1/4,則f*40%<=閾值<=f*60%,取該范圍內若干代表閾值,例如,額可以取如下代表閾值:f*40%,f*45%,f*50%,f*55%,f*60%,計算每個閾值點對應的基于學習的稀疏表示圖像超分辨率重建算法的重建時間和重建后圖像的分辨率,可以根據主觀評價和psnr來判斷。然后根據使用者需求從若干代表閾值中確定固定閾值,如使用者需求更注重時間,那就調高比例,時間就快;相反使用者如果注重重建效果,那就調低比例,帶來的就是重建效果較好但時間較長。例如,經計算后f*50%最符合使用者需求,則取固定閾值=f*50%。
s22d:輸入步驟s21獲得的待重建的低分辨率圖像塊,采用邊緣提取算法提取圖像塊邊緣信息,當該圖像塊信息量不超過步驟s22c確定的固定閾值時該圖像塊為低信息量圖像塊;否則,為高信息量圖像塊。優選地,所述邊緣提取算法為canny算子邊緣檢測算法。
s23:針對高信息量圖像塊進行圖像濾波操作,進行高頻特征提取,采用二維濾波算子濾波器組,所用濾波器組為f={f1,f2,f3,f4},其由四個不同的濾波器組成,分別為:
f1=[1,-1],f2=f1t
(4)
f3=log,f3=f3t
(5)
其中上角標t表示矩陣轉置操作,log代表一種5×5的二維濾波算子。經過高頻特征提取操作后獲得圖像塊高頻信息,以xl表示。
s24:對步驟s23獲得的圖像塊進行kpca降維,實現高維數據壓縮。降維步驟如下:
s24a:將高維數據集合表示為x={x1,x2,x3,…,xm},xi∈rd,kpca方法經過非線性映射函數x→φ(x)∈f,其中f是特征空間,這樣便能將每個數據x映射到一個高維特征空間。
s24b:核函數通過φ將進行一個點x到f的對應操作,并且由此獲得的f數據滿足中心化的條件,即:
則特征空間f中的協方差矩陣為:
s24c:求c的特征值λ≥0以及特征向量
v∈f\{0},cv=λv(8)
則有
(φ(xv)·cv)=λ(φ(xv)·v)(9)
考慮到所有的特征向量可表示為φ(x1),φ(x2),…,φ(xm)的線性組合,即:
則有:
式中,v=1,2,3,…,m,定義m×m維矩陣kμv
kμv:=(φ(xμ)·φ(xv))(12)
s24d:求解上式得到特征值及特征向量,對于數據集合在特征向量空間vk的投影可以寫成:
那么,數據被投影到協方差矩陣的特征向量vk上,投影結果(也就是低維數據的表示y)可以表示為:
s25:對經過步驟s24降維壓縮后的數據進行基于學習的稀疏表示圖像超分辨率重建,具體步驟如下:
s25a:采用omp算法對步驟s24d獲得的低維數據y在低分辨率字典dl下的稀疏表示系數β,即求解如下方程:
其中t0為給定的稀疏度,βi為矩陣β中的子元素。
s25b:將求得的稀疏表示系數β與高分辨率字典dh相乘,得到重建的高信息量重建子區域,即:
x=dhβ
其中x為求得的超分辨率子區域。
s26:將步驟22d獲得的低信息量圖像塊采用雙三次插值算法進行重建得到低信息量重建子區域;
s27:將高信息量子區域與所述低信息量重建子區域進行圖像拼接得到超分辨率重建圖像;
s28:采用雙三次插值算法將所述超分辨率重建圖像進行m倍插值得到n*m(n=2,3,4;m>0)倍的超分辨率重建圖像。
以上內容是結合具體的優選實施方式對本發明所作的進一步詳細說明,不能認定本發明的具體實施只局限于這些說明。對于本發明所屬技術領域的普通技術人員來說,在不脫離本發明構思的前提下,還可以做出若干簡單推演或或替換,都應當視為屬于本發明的保護范圍。
- 還沒有人留言評論。精彩留言會獲得點贊!