一種判斷送絲風機抖振的綜合分析及其驗證方法與流程
本發明涉及一種卷煙風力送絲領域,尤其涉及送絲風機抖振判斷的綜合分析及其驗證方法。
背景技術:
煙絲是制造卷煙的重要原料之一。在卷煙生產過程中,首先煙絲經過切割、發酵、加濕、添加成分、烘干等工藝流程,通過輸送環節到達卷煙機集絲箱;然后卷煙機通過煙絲成型后形成煙條,再由重量控制系統將煙條切割成重量均等的卷煙,最后卷煙通過包裝機形成小包和大條。這個過程中,煙絲作為重要的和唯一的流通介質,所以在輸送環節中煙絲是否能夠保質保量是決定卷煙產品質量高低的重要因素之一。
風力送絲由于其具有響應速度快、配置靈活、可靠性高等特點被大多數煙草企業所采用,風力送絲依靠送絲風機提供負壓吸風,將集絲箱內的煙絲通過送絲管道送往卷煙機生產卷煙,在此過程中,送絲風機受電流波動和風管內風阻影響,送絲風機會產生抖振,當風機產生抖振時,原本勻速規則的空氣流會變得不穩定,產生很多不規則的亂流,稱作“紊流”。雖然紊流的產生時間相對整個吸絲過程時間微不足道,但仍然會造成煙絲輸送的異常,異常現象表現在:當吸絲風速偏低時,就容易產生煙絲偏少或煙絲堵塞的現象,最終導致卷煙機停機;當吸絲風速偏高時,就會增加煙絲與管壁的碰撞與摩擦,增加煙絲的造碎,直接影響煙絲的長絲率等工藝質量指標。另外,頻繁的抖振會損壞風機風葉,加速風機內運動部件磨損。一般風機的抖振頻率都是由低到高,不間斷發生,為此,如何結合風機動力學特性,避免風機抖振,是研究送絲過程穩定性的難題,參考其它設備減小抖振的方法,對此提出的方法有很多。例如安徽科技學院(喬印虎,易克傳,等.智能材料的風機葉片振動主動控制分析[j].檢測與控制,2009,(9):118-120)提出兩種減小設備抖振的控制策略,即主動阻尼策略和變頻控制策略,主動阻尼策略通過調整阻尼比使抖振得到有效衰減或抑制,變頻控制策略通過保證系統的主要振動模態不被激發或強迫振動能量向著易于耗散的模態傳遞,從而達到控制抖振的目的。廣東工業大學(李忠娟,張新政.變結構控制理論中抖振問題的研究[j].五邑大學學報,2003,17(3):66-69)在分析了常見的四種用于削弱抖振的方法后,提出了基于模糊神經的抖振方法并利用仿真結果以證明。北京理工大學(于亞男,孫博,等.基于新型趨近律的撓性航天器滑模變結構控制[j].航天控制,2013,31(5):62-68)針對應用切換函數帶來的撓性航天器滑模變結構控制力矩的高頻抖振問題,提出了應用模糊邏輯對改進后的指數趨近率進行自適應智能處理,從而抑制控制力矩的高頻抖振。哈爾濱工程大學(金鴻章,羅延明,等.抑制滑模抖振的新型飽和函數法研究[j].哈爾濱工程大學學報,2007,28(3):288-291)提出了一種具有動態邊界層的飽和函數控制方法,該方法可使邊界層隨狀態軌跡的收斂而逐漸收縮,從而降低狀態軌跡中的抖振頻率。中國礦業大學(鄭車曉,孫偉,等.變結構控制一種抑制抖振的方法設計[j].中國科技論文在線,2011)設計了一種將趨近律與傳統pid控制方法及采用飽和函數為切換函數的傳統變結構控制進行比較,從而得到一種新的具有良好控制效果的削弱抖振的方法。西安電子科技大學(申宇.滑模變結構控制中抖振的特性研究與抑制[d].西安電子科技大學學士學位論文,2012)提出了一種采用廣義描述函數法穩定判據和變結構切換增益自適應調節方法,用來設計具有較小抖振特性的齒隙補償控制器和兩類二階采樣變結構控制器。軍械工程學院(席雷平,陳自力,等.具有抖振抑制特性機械臂快速滑模變結構控制[j].電機與控制學報,2012,16(7):97-102)提出了一種基于新型滑模面和模糊冪次趨近律的滑模變結構控制策略,提高了滑模變結構控制滑動運動階段的收斂速度,能夠在保證抖振抑制效果的前提下,提高系統的趨近運動速度。福州大學機械工程及自動化學院(童超,陳力.基于模糊冪次趨近律的漂浮基空間機器人快速滑模變結構控制[j],2015,10(3):45-51)討論了一種基于模糊冪次趨近律的快速滑模變結構控制方法,該方法能夠使機械臂抖振抑制的效果明顯,同時也保證了系統的軌跡跟蹤控制效果。清華大學(楊普,張曾科.一類滑模變結構控制系統的抖振控制[j],2005,45(1):34-42)通過分析指數趨近率下滑模變結構控制的抖振過程,給出了抖振幅度、周期和趨近率參數、控制量的變化率之間的定量關系,以減弱塞棒以一定幅度和頻率的抖振。湖南工業大學(黃華,李光,等.基于趨近律的機械臂滑模控制方法研究[j],2013,27(1):62-66)分析和設計了指數趨近律,以此為基礎,研究和優化了機械臂的運動學特性,減小機械臂在運動過程中的抖振。
抖振是風機設備在運行過程中常見的現象,輕微的抖振是正常現象,但如果頻繁的或是有嚴重異響的抖振是會影響風葉內部零部件的使用壽命,造成不可逆轉的損傷。由于風機是一個封閉的運行環境,風機抖振都是由輕微逐漸發展為嚴重的過程,當產生嚴重抖振時就必須停機維修,更換部件,這會造成生產影響和經濟損失,所以如何預先判斷風機抖振狀況,以抑制或消除抖振趨勢,是降低風機系統故障影響風險的措施之一。上述文獻更多的是采用調整趨近律的方法,來判斷是否減小抖振的幅度、周期和變化率,這適用于具有相對強抗干擾性、間斷擾動的物體,但由于風機受本身系統參數和外部環境(電流,強磁場)的影響較大,抗干擾特性相對較弱,容易產生無法測知的持續擾動,所以嚴格意義上來說,采用調整趨近律的方法判斷對于具有不可測知且持續擾動的風機系統是沒有意義的。
技術實現要素:
本發明要解決的技術問題是提供一種判斷送絲風機抖振的綜合分析及其驗證方法,將約束式預期控制引入到對判斷送絲風機抖振的綜合分析及其驗證方法中,通過對預期控制系數σ和模態量化系數c推演出引起風機抖振的發生過程,較好的解決了短時間、偶發性和高頻次等因素影響下的風機抖振原因不確定、分析不準確及驗證難以實現的問題。
本發明為解決上述技術問題所采用的技術方法是:
一種判斷送絲風機抖振的綜合分析及其驗證方法,該方法包括綜合分析和驗證方法,所述的綜合分析包括以下的步驟:
1)在一個設備送線時段內隨機對送絲風機負壓吸風的瞬時風壓和風量的過程變量進行采樣,獲得采樣矩陣w=(n*s),其中n為采樣點個數,s為監測變量個數;重復t個生產時段,獲得相應的數據矩陣w'=(t*n*si),其中si為第i個除塵時段內的采樣點個數;
2)所述的數據矩陣按照約束變分原理進行測算,獲得針對送絲風機抖振的約束控制系數σ,即
3)所述的送風過程設定為兩階函數,對其送風系統進行調控:當風機工作處于穩定時,則有y=x,其中y0=y,x0=x,其中y為振幅,x為振動頻率,其啟停切換條件為
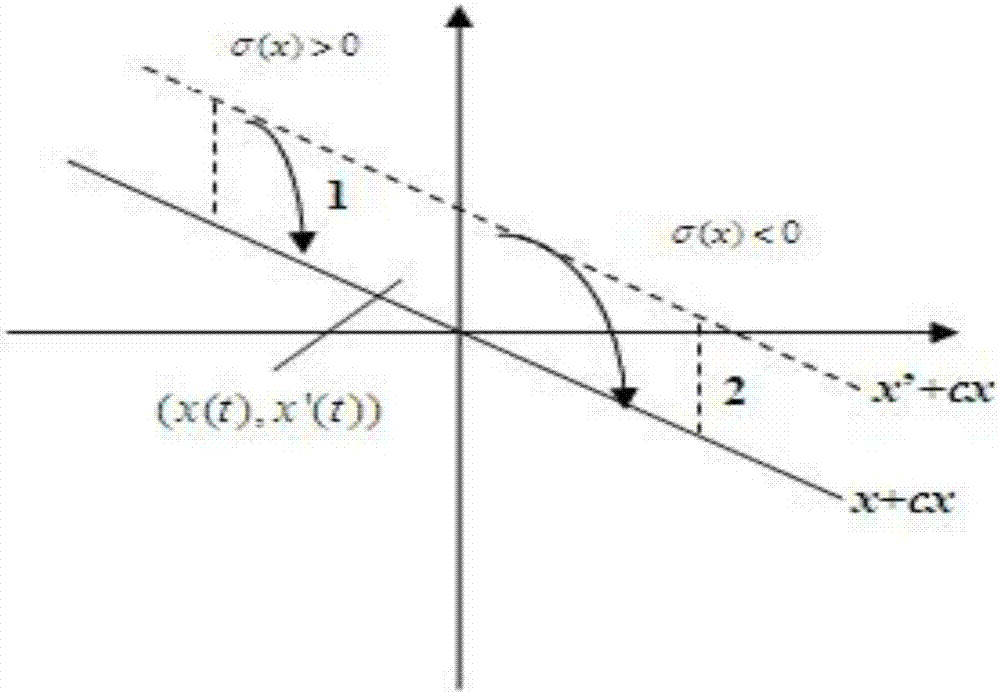
3)所述的送風系統若是可以調控的,那么按照此前調控方法設計出來的系數σ能夠保證送風系統符合(x0',xσ')的初始值,即在trc=tσ-t0期間,tσ為送風系統約束控制過程時間,t0為送風系統初始狀態時間,trc為送風系統約束預期控制時間;使送風系統從(x0',xσ')的初始狀態到達c模態量化狀態,這個過程是便于風機能夠符合約束式預期控制的量化狀態,過程如圖1所示;
4)所述的圖1,圖中(x0',xσ')與原點o(0,0)之間連線的斜率表示為d=-xσ/x0;σ>0相當于δd=xσ-x0>0,在風機送風系統狀態趨近量化狀態c期間,必有d<0,故x+dx=0所代表的風機送風系統工況模態收斂速度不同于c所代表的工況模態收斂速度,也就是說風機送風系統在還未完全量化狀態下的工況模態收斂速度大于約束式預期控制狀態下所代表的工況模態收斂速度,風機的抖振還比較明顯;在送風系統從(x0',xσ')向c的趨近過程中,其收斂速度逐漸減小到與c的收斂速度一致,即d→c,該趨近過程稱為平衡,反之,則為抖振;
5)所述的系數σ在風機啟停切換條件(σ'<0,σ>0)下求解出來的c存在有可能不同于在送風系統工況模態收斂狀態下設計出來的c等價的現象,因為風機產生抖振時的σ有超過極限值的可能,所以不能保證風機一直處于穩定狀態,若在送風系統工況模態收斂后仍然發生風機抖振,則必出現預期控制不可實現的現象;
6)所述的當出現預期調控不可實現的現象時,此時的斜率d不等于c,與x+cx=0平行的直線x'+cx≠0,即風機送風系統模態量化的狀態無法滿足約束式條件,所以送風系統無法起到預期調控的意義;雖然它的斜率不等于量化系數c,但可以將x+cx≠0上下平移;所以可采用平移的辦法將斜率等于c,結果是收斂的變化過程(即(x(t),x'(t)))有兩種可能,如圖2所示,其中第1種可能說明風機抖振可調控,第2種可能說明風機抖振不可調控;
7)所述的圖2中,曲線1表明風機發生抖振時可調控,曲線2表明不可調控,在風機送風系統趨近量化c期間,因d>0送風系統收斂過程必先發散,而后演化為量化c的另一分支,則風機抖振趨向穩定的過程是非單向收斂過程;
8)所述的驗證上述分析正確與否的方法包括兩個步驟,第一個步驟是確定風機送風系統的啟停切換函數σ(x);第二個步驟是通過滿足模態量化狀態系數c來達到預期控制的目的;
第一個步驟包括以下的步驟:
1)所述的第一個步驟中,假定將風機抖振控制問題的對象,即風機工況狀態表示為:s=a(x)+b(y)*0.5,其中a(x)表示振動頻繁變化矩陣,b(y)表示振幅變化矩陣,c表示模態量化系數;由于a(x)是n×n維矩陣,b(y)是n×m維矩陣,所以s是n維向量,c∈rm×n,則風機送風系統的啟停切換函數σ(x)指定為狀態變量線性組合而成的函數等價為:σ(x)=s=a(x)+b(y)*c;
2)所述的函數等式中,模態量化系數c∈rm×n,它是切換函數的線性組合系數,其被控對象可表示為矩陣:
3)所述的風機模態量化系數c的取值范圍,若想減小風機抖振,滿足方法漸近穩定性的要求,僅需c>0,根據x1可能變化的范圍以及對預期調控方法動態過程快速性要求來減小抖振,例如指定c=0.5,則風機工況狀態s定義為:x2=-0.5x1,-2<x1<2,它是s的存在區域θσ中,斜對稱于零點的兩條線段s1和s2,如圖3所示,圖中θσ為s的領域;如果希望持續減弱抖振,而且對方法快速性沒有特定要求,則僅需減小c且c>0,使方法快速性遠低于送風系統快速性即可;
第二個步驟包括以下的步驟:
1)所述的第二個步驟中,c將送風系統從x0拉到s上的途徑有兩條:σ(x)>0將x拉到sp上,或σ(x)<0將x拉到sn上為穩定,其中sp為預估狀態,sn為調控狀態;σ(x)>0將x拉到sn上,或σ(x)<0將x拉到sp上為抖振;雖然它們都到達了s,但動態過程x0(t)不同;若穩定,x0(t)單向收斂無超調;若抖振,x0(t)則超調;穩定還是抖振,取決于c的確定方法;
2)所述的途徑,利用此條件,獲取控制的不等式為
3)所述的約束式預期控制的誤差系數u’的表達式,即u'=-csgn(σ(x))與被控對象表達式兩者形成了閉環控制;
4)所述的誤差系數u的表達式進行舉例,例如將
本發明將約束式預期控制引入到對判斷送絲風機抖振的綜合分析及其驗證方法中,通過對預期控制系數σ和模態量化系數c推演出引起風機抖振的發生過程,較好的解決了短時間、偶發性和高頻次等因素影響下的風機抖振原因不確定、分析不準確及驗證難以實現的問題。
附圖說明
圖1為系統趨近可調控狀態過程圖。
圖2為(x(t),x'(t))變化過程的兩種可能圖。
圖3為系統漸近穩定性過程圖。
圖4為本發明和系統框圖。
具體實施方式
如圖4所示的一種判斷送絲風機抖振的綜合分析及其驗證方法,該方法包括綜合分析和驗證方法,所述的綜合分析包括以下的步驟:
1)在一個設備送線時段內隨機對送絲風機負壓吸風的瞬時風壓和風量的過程變量進行采樣,獲得采樣矩陣w=(n*s),其中n為采樣點個數,s為監測變量個數;重復t個生產時段,獲得相應的數據矩陣w'=(t*n*si),其中si為第i個除塵時段內的采樣點個數;
2)所述的數據矩陣按照約束變分原理進行測算,獲得針對送絲風機抖振的約束控制系數σ,即
3)所述的送風過程設定為兩階函數,對其送風系統進行調控:當風機工作處于穩定時,則有y=x,其中y0=y,x0=x,其中y為振幅,x為振動頻率,其啟停切換條件為
3)所述的送風系統若是可以調控的,那么按照此前調控方法設計出來的系數σ能夠保證送風系統符合(x0',xσ')的初始值,即在trc=tσ-t0期間,tσ為送風系統約束控制過程時間,t0為送風系統初始狀態時間,trc為送風系統約束預期控制時間;使送風系統從(x0',xσ')的初始狀態到達c模態量化狀態,這個過程是便于風機能夠符合約束式預期控制的量化狀態,過程如圖1所示;
4)所述的圖1,圖中(x0',xσ')與原點o(0,0)之間連線的斜率表示為d=-xσ/x0;σ>0相當于δd=xσ-x0>0,在風機送風系統狀態趨近量化狀態c期間,必有d<0,故x+dx=0所代表的風機送風系統工況模態收斂速度不同于c所代表的工況模態收斂速度,也就是說風機送風系統在還未完全量化狀態下的工況模態收斂速度大于約束式預期控制狀態下所代表的工況模態收斂速度,風機的抖振還比較明顯;在送風系統從(x0',xσ')向c的趨近過程中,其收斂速度逐漸減小到與c的收斂速度一致,即d→c,該趨近過程稱為平衡,反之,則為抖振;
5)所述的系數σ在風機啟停切換條件(σ'<0,σ>0)下求解出來的c存在有可能不同于在送風系統工況模態收斂狀態下設計出來的c等價的現象,因為風機產生抖振時的σ有超過極限值的可能,所以不能保證風機一直處于穩定狀態,若在送風系統工況模態收斂后仍然發生風機抖振,則必出現預期控制不可實現的現象;
6)所述的當出現預期調控不可實現的現象時,此時的斜率d不等于c,與x+cx=0平行的直線x'+cx≠0,即風機送風系統模態量化的狀態無法滿足約束式條件,所以送風系統無法起到預期調控的意義;雖然它的斜率不等于量化系數c,但可以將x+cx≠0上下平移;所以可采用平移的辦法將斜率等于c,結果是收斂的變化過程(即(x(t),x'(t)))有兩種可能,如圖2所示,其中第1種可能說明風機抖振可調控,第2種可能說明風機抖振不可調控;
7)所述的圖2中,曲線1表明風機發生抖振時可調控,曲線2表明不可調控,在風機送風系統趨近量化c期間,因d>0送風系統收斂過程必先發散,而后演化為量化c的另一分支,則風機抖振趨向穩定的過程是非單向收斂過程;
8)所述的驗證上述分析正確與否的方法包括兩個步驟,第一個步驟是確定風機送風系統的啟停切換函數σ(x);第二個步驟是通過滿足模態量化狀態系數c來達到預期控制的目的;
第一個步驟包括以下的步驟:
1)所述的第一個步驟中,假定將風機抖振控制問題的對象,即風機工況狀態表示為:s=a(x)+b(y)*0.5,其中a(x)表示振動頻繁變化矩陣,b(y)表示振幅變化矩陣,c表示模態量化系數;由于a(x)是n×n維矩陣,b(y)是n×m維矩陣,所以s是n維向量,c∈rm×n,則風機送風系統的啟停切換函數σ(x)指定為狀態變量線性組合而成的函數等價為:σ(x)=s=a(x)+b(y)*c;
2)所述的函數等式中,模態量化系數c∈rm×n,它是切換函數的線性組合系數,其被控對象可表示為矩陣:
3)所述的風機模態量化系數c的取值范圍,若想減小風機抖振,滿足方法漸近穩定性的要求,僅需c>0,根據x1可能變化的范圍以及對預期調控方法動態過程快速性要求來減小抖振,例如指定c=0.5,則風機工況狀態s定義為:x2=-0.5x1,-2<x1<2,它是s的存在區域θσ中,斜對稱于零點的兩條線段s1和s2,如圖3所示,圖中θσ為s的領域;如果希望持續減弱抖振,而且對方法快速性沒有特定要求,則僅需減小c且c>0,使方法快速性遠低于送風系統快速性即可;
第二個步驟包括以下的步驟:
1)所述的第二個步驟中,c將送風系統從x0拉到s上的途徑有兩條:σ(x)>0將x拉到sp上,或σ(x)<0將x拉到sn上為穩定,其中sp為預估狀態,sn為調控狀態;σ(x)>0將x拉到sn上,或σ(x)<0將x拉到sp上為抖振;雖然它們都到達了s,但動態過程x0(t)不同;若穩定,x0(t)單向收斂無超調;若抖振,x0(t)則超調;穩定還是抖振,取決于c的確定方法;
2)所述的途徑,利用此條件,獲取控制的不等式為
3)所述的約束式預期控制的誤差系數u’的表達式,即u'=-csgn(σ(x))與被控對象表達式兩者形成了閉環控制;
4)所述的誤差系數u的表達式進行舉例,例如將
- 還沒有人留言評論。精彩留言會獲得點贊!