一種基于自適應特征降維的多標記數據分類方法與流程

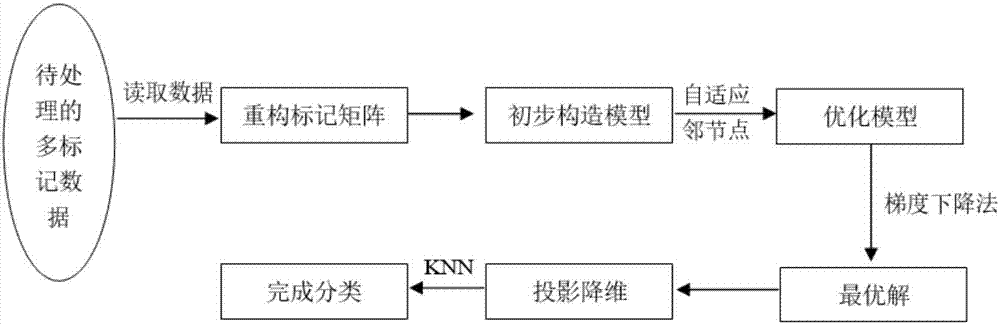
本發明屬于機器學習
技術領域：
，涉及一種基于自適應特征降維的多標記數據分類方法，用于數據挖掘和大數據中，對包含噪聲、特征復雜的多標記數據進行分類。
背景技術：
：隨著計算能力、存儲、網絡的高速發展，人類積累的數據量正以指數速度增長。對于這些數據，人們迫切希望從中提取出隱藏其中的有用信息，更需要發現更深層次的規律，對決策，商務應用提供更有效的支持。為了滿足這種需求，數據挖掘技術的得到了長足的發展，而多標記數據的分類在數據挖掘中是一項非常重要的任務，目前在商業上應用最多。多標記數據，是指數據中一個樣本同時屬于多個類別，例如在圖像分類任務中，一個圖像同時包含“山川”和“河流”，一個文件可能同時屬于“環保”和“健康”類別，一個基因同時屬于“變異基因”和“復制基因”。多標記數據的特征是人為規定，多標記是先驗信息，事前已知的。數據特征是指人為規定的對數據的描述方法，例如圖像數據，特征可以是每個圖像樣本的像素的灰度值所組成的矩陣；文本數據，特征可以是每個文本樣本的總字數，特定字符出現的頻率等組成的矩陣。所獲取的原始數據特征一般所處高維空間，包含信息冗余較大，應用于分類任務中，計算復雜度高，效率低，并且容易受噪聲數據影響，準確度不高。因此，傳統的分類方法不能很好的應用于數據挖掘的分類過程。技術實現要素：針對上述現有技術中存在的問題，本發明的目的在于，提供一種基于自適應特征降維的多標記數據分類方法，以解決現有的分類方法計算復雜度高，準確度低的缺點，提高分類任務的性能。為了實現上述任務，本發明采用以下技術方案：一種基于自適應特征降維的多標記數據分類方法，包括以下步驟：步驟一，讀取已知分類的多標記數據，分別將已知分類的多標記數據的特征和標記存儲為特征矩陣x和標記矩陣y；讀取待分類的多標記數據，將待分類的多標記數據的特征存儲為矩陣t；步驟二，將標記矩陣y重構為潛在語義矩陣v和系數矩陣b以降低標記矩陣y中噪聲的影響；步驟三，引入投影矩陣w，利用截斷范數構造降維模型如下：上式中，xi是特征矩陣x的第i行，n是特征矩陣x的行數，即特征矩陣x中的樣本個數；vi是潛在語義矩陣v的第i行，||·||f是f-范數，||·||2是2-范數，α和γ是系數，取值范圍為(0,1]；步驟四，在降維模型中加入幾何結構約束，以使降維前后數據的局部幾何結構保持一致；步驟五，利用降維模型構造目標函數，采用梯度下降法對目標函數進行迭代，直到目標函數收斂，得到投影矩陣w的最優解；步驟六，對已知分類的多標記數據、待分類的多標記數據進行投影降維處理，并對降維后的數據進行分類處理，完成。進一步地，步驟二中進行標記矩陣y重構時需要滿足的公式為：上式中，表示f-范數的平方，y為n×k的矩陣，v為n×c的矩陣，b為c×k的矩陣。n,c,k分別是矩陣中樣本的個數、重構中聚類的個數、標記的個數。進一步地，步驟四的具體過程包括：步驟4.1，根據特征矩陣x計算相似度矩陣s的第i行第j列元素：上式中，xi、xj分別是特征矩陣x的第i行和第j列向量，σ2是特征矩陣x的方差；步驟4.2，定義拉普拉斯矩陣l：l＝a-s其中對角矩陣a的第i行第i列元素n是相似度矩陣s中樣本的個數；步驟4.3，加入幾何結構約束，構造模型如下：上式中，β是系數，0＜β≤1，tr(·)表示矩陣的跡，ε為參數，取值范圍為(0,0.1]。進一步地，步驟五的具體過程包括：步驟5.1，構造目標函數j如下：為了方便求偏導數和迭代，對目標函數變形得：其中矩陣f的第i行第i列元素ind(·)表示滿足條件值為1，不滿足條件值為0；步驟5.2，目標函數j(w,v,b)分別對w，v，b求偏導數：步驟5.3，梯度下降過程，w、v、b的更新規則如下：其中，λv，λb，λw為梯度下降的步長，取值范圍均為(0,1]；步驟s54，對w、v、b分別賦予隨機初值，代入目標函數j(w,v,b)，求得的值記為；利用步驟s53中的變量更新規則，得到新的變量w',v',b',再代入目標函數j(w',v',b')，求得的值記為j'；計算目標函數的下降程度g＝j'-j，若g＞10^-3，則循環上述步驟，直到g≤10^-3，此時輸出投影矩陣w，即為最優化解。進一步地，步驟六中進行投影降維處理的過程為：根據步驟五中得到的投影矩陣w，已知分類的多標記數據特征矩陣x的自適應降維后的特征矩陣x'，如下：x'＝x*w待分類的多標記數據特征矩陣自適應降維后的特征矩陣t'，如下：t'＝t*w進一步地，步驟六中進行分類處理的過程為：計算特征矩陣t'中第i個樣本與特征矩陣x'第j個樣本之間的距離dij：dij＝|x′i-t′j|i,j＝1,2,…n其中n為特征矩陣x'中樣本個數；對第i個樣本與其他樣本之間的距離進行升序排列：{di1,di2,di3…dik…din}然后統計距離第i個樣本最近的個樣本中，統計出現頻率最多的類標記，即為第i個樣本的所屬分類。本發明與現有技術相比具有以下技術特點：1.本發明投影矩陣的最優化求解過程，對高維特征的數據，進行線性變換，投影到低維空間，有效的降低分類任務中數據的復雜程度，去除冗余特征，保留有辨識度的特征，很好的解決了傳統方法導致計算復雜度高的問題，提高了數據分類的效率。2.本發明構造降維模型的過程，利用多標記數據的標記矩陣，通過聚類得到潛在語義信息，有效解決了原始數據中噪聲對分類準確率的影響，提高了數據分類的準確率。附圖說明圖1為本發明方法的流程圖；具體實施方式一、方法詳細步驟本發明提供了一種基于自適應特征降維的多標記數據分類方法，包括以下步驟：步驟一，數據讀取利用matlab讀取已知分類的多標記數據，分別將已知分類的多標記數據的特征和標記存儲為特征矩陣x和標記矩陣y；讀取待分類的多標記數據，將待分類的多標記數據的特征存儲為矩陣t；步驟二，重構標記矩陣將標記矩陣y重構為潛在語義矩陣v和系數矩陣b以降低標記矩陣y中噪聲的影響；具體地：為了降低標記矩陣y中噪聲的影響，將y重構為兩個更低維度的潛在語義矩陣v和系數矩陣b。并且重構誤差最小，需滿足下式：上式中，表示f-范數的平方，y為n×k的矩陣，v為n×c的矩陣，b為c×k的矩陣。n,c,k分別是矩陣中樣本的個數、重構中聚類的個數、標記的個數。特征矩陣和表即矩陣為同一個數據集不同方面的描述，其中的樣本個數n是相同的。步驟三，構造降維模型引入投影矩陣w，利用截斷范數構造降維模型如下：上式中，xi是特征矩陣x的第i行，n是特征矩陣x的行數，即特征矩陣x中的樣本數；vi是潛在語義矩陣v的第i行，||·||f是f-范數，||·||2是2-范數，α和γ是系數，取值范圍為(0,1]；投影矩陣w是d×c的矩陣，d是樣本特征的維數，c是重構中聚類的個數。降維模型中第一項和第三項就是表達對w的要求，第一項最小化公式要求投影矩陣w要使得投影后的特征矩陣與潛在語義矩陣的誤差盡可能小，第三項f-范數要求投影矩陣w每一個元素都盡可能小，從而使得模型泛化能力強。因為潛在語義矩陣v減少了多標記矩陣y中噪聲的影響，所以我們利用回歸模型和潛在語義矩陣v的優勢，構造上述降維模型同時進行了標記矩陣y的重構和降維，同時也加強了降維過程的魯棒性。步驟四，在降維模型中加入幾何結構約束，以使降維前后數據的局部幾何結構保持一致；步驟4.1，根據特征矩陣x計算相似度矩陣s的第i行第j列元素：上式中，xi、xj分別是特征矩陣x的第i行和第j列向量，σ2是特征矩陣x的方差；步驟4.2，定義拉普拉斯矩陣l：l＝a-s其中對角矩陣a的第i行第i列元素n是相似度矩陣s中樣本的個數，也是行數或列數；矩陣的每個元素代表了任意兩個樣本之間的相似程度；步驟4.3，為了使降維前后數據的局部幾何結構保持一致，加入幾何結構約束，構造模型如下：上式中，β是系數，0＜β≤1，tr(·)表示矩陣的跡，ε為參數，取值范圍為(0,0.1]，其余參數含義同步驟三中的降維模型。步驟五，利用步驟四處理后的降維模型構造目標函數，采用梯度下降法對目標函數進行迭代，直到目標函數收斂，得到投影矩陣w的最優解；步驟5.1，構造目標函數j如下：為了方便求偏導數和迭代，對目標函數變形得：其中矩陣f的第i行第i列元素ind(·)表示滿足條件值為1，不滿足條件值為0；驟5.2，目標函數j(w,v,b)分別對w，v，b求偏導數：步驟5.3，梯度下降過程，w、v、b的更新規則如下：其中，λv，λb，λw為梯度下降的步長，取值范圍均為(0,1]；根據目標函數的趨勢確定，當目標函數下降太慢時，將步長調大，當步長過大，而導致目標函數上升時，再將步長調小。步驟s54，對w、v、b分別賦予隨機初值，代入目標函數j(w,v,b)，求得的值記為；利用步驟s53中的變量更新規則，得到新的變量w',v',b',再代入目標函數j(w',v',b')，求得的值記為j'；計算目標函數的下降程度g＝j'-j，若g＞10^-3，則循環上述步驟，直到g≤10^-3，此時輸出投影矩陣w，即為最優化解。步驟六，對已知分類的多標記數據、待分類的多標記數據進行投影降維處理，并對降維后的數據進行分類處理，完成；具體地：進行投影降維處理的過程為：根據步驟五中得到的投影矩陣w，已知分類的多標記數據特征矩陣x的自適應降維后的特征矩陣x'，如下：x'＝x*w待分類的多標記數據特征矩陣自適應降維后的特征矩陣t'，如下：t'＝t*w進行分類處理的過程為：計算特征矩陣t'中第i個樣本與特征矩陣x'第j個樣本之間的距離dij：dij＝|x′i-t′j|i,j＝1,2,…n其中n為特征矩陣x'中樣本個數；對第i個樣本與其他樣本之間的距離進行升序排列：{di1,di2,di3…dik…din}然后統計距離第i個樣本最近的個樣本中，統計出現頻率最多的類標記，即為第i個樣本的所屬分類。二、仿真實驗對本發明中提出的多標記降維方法的仿真。仿真條件是matlabr2014b64位軟件下進行。本實驗以mrboutell等人于2004年在patternrecognition上發表的論文“learningmulti-labelsceneclassification”中的數據集scene作為仿真實驗的數據，包含1211個訓練樣本，1196個測試樣本，294維特征，6個標記。分別對比本發明方法與主成分分析(pca)，線性判別式(lda)，局部保持投影(lpp)將特征降低到100維后的在各標記上的分類準確率和總的時間耗費。表1本發明方法與pca、lda、lpp的準確率對比表2本發明方法與pca、lda、lpp的耗費時間對比方法pcaldalpp本發明方法時間(秒)1218218058結合表1和表2中的實驗數據，本發明的多標記數據分類方法在4個標記的準確率都是高于其他三種方法，并且完成分類任務的時間成本明顯低于其他方法。因此，實驗結果表明，本發明在大多數情況下具有高準確率、高效率等優點。當前第1頁12