一種網格開槽殼體的軸壓承載折減因子的預測方法與流程
本發明屬于戰術導彈結構強度設計分析技術領域,尤其涉及一種網格開槽殼體的軸壓承載折減因子的預測方法。
背景技術:
薄壁結構具有輕質和承載性能良好等特點,被廣泛應用于彈箭體艙段結構設計中。為滿足撞擊測量光纖的鋪設要求,某型靶彈末修艙和儀器艙金屬殼體采用了一種光筒殼外刻光纖槽的結構形式。相比傳統的網格加筋和蒙皮桁條式薄壁結構形式,設計人員對這種新型網格開槽殼體的力學承載性能缺乏工程經驗,尤其是其承受軸向壓力載荷時的穩定性折減因子缺乏工程化的預測方法,進而無法確定殼體的軸壓承載能力。
近年來,薄壁筒殼結構軸壓承載能力確認技術得到了國內外多家研究機構的重視,并且一致認為精細化仿真分析與折減因子預測理論與方法是未來航天結構減重的重要途徑。無獨有偶,多家機構均采用缺陷敏感性分析模型,通過虛擬試驗和實物試驗相結合的方法來對折減因子進行預測。然而,這種方法仍然需要大量實驗驗證來提供確定折減因子所需的概率密度信息,難以適用于戰術型號快速化和低成本的設計要求。因此,圍繞戰術導彈用網格開槽薄壁殼體,研究一種快速化的折減因子的預測方法,具有重要的工程意義。
技術實現要素:
本發明的技術解決問題:克服現有技術的不足,提供一種網格開槽殼體的軸壓承載折減因子的預測方法,用于預測薄壁網格開槽殼體軸壓極限載荷折減因子,以確定殼體承載能力是否滿足設計要求。
為了解決上述技術問題,本發明公開了一種網格開槽殼體的軸壓承載折減因子的預測方法,包括:
步驟1,建立網格開槽殼體對應的有限元模型;
步驟2,在網格開槽殼體中部橫縱開槽交匯位置施加單一指定位移載荷,根據所述有限元模型和施加的單一指定位移載荷進行靜力分析,得到含初始單點凹陷缺陷的非完美結構模型;
步驟3,對所述含初始單點凹陷缺陷的非完美結構模型進行非線性后屈曲分析,得到軸壓極限載荷;
步驟4,通過改變所述單一指定位移載荷的大小,得到單點凹陷程度對軸壓承載的缺陷敏感性曲線;其中,所述單點凹陷程度對軸壓承載的缺陷敏感性曲線,用于指示不同初始單點的凹陷缺陷程度的軸壓極限載荷;
步驟5,根據所述單點凹陷程度對軸壓承載的缺陷敏感性曲線的收斂性,確定被引入單點凹陷缺陷程度;
步驟6,針對確定的被引入單點凹陷缺陷程度,通過改變單點凹陷的軸向位置,得到含初始單點凹陷缺陷的非完美結構模型集合;
步驟7,根據所述含初始單點凹陷缺陷的非完美結構模型集合,確定單點凹陷位置對軸壓承載的缺陷敏感性曲線;
步驟8,根據所述單點凹陷程度對軸壓承載的缺陷敏感性曲線和所述單點凹陷位置對軸壓承載的缺陷敏感性曲線,得到所述網格開槽殼體的軸壓承載折減因子的預測結果。
在上述網格開槽殼體的軸壓承載折減因子的預測方法中,所述建立網格開槽殼體對應的有限元模型,包括:
當所述網格開槽殼體為截錐形網格開槽金屬殼體時,采用六面體實體單元對所述網格開槽殼體為截錐形網格開槽金屬殼體進行離散,建立所述有限元模型;其中,所述截錐形網格每個節點包括三個平動自由度,所述有限元模型的下端固支,上端面節點與端面圓心位置參考點剛性耦合、且參考點除軸向位移外的其余所有自由度被約束。
在上述網格開槽殼體的軸壓承載折減因子的預測方法中,所述在網格開槽殼體中部橫縱開槽交匯位置施加單一指定位移載荷,根據所述有限元模型和施加的單一指定位移載荷進行靜力分析,得到含初始單點凹陷缺陷的非完美結構模型,包括:
在網格開槽殼體中部橫縱開槽交匯位置施加單一指定位移載荷,采用非線性隱式靜力學法進行幾何大變形靜力分析,得到單點凹陷變形分布;
根據所述單點凹陷變形分布確定凹陷區域節點位移量;
將所述凹陷區域節點位移量疊加至有限元模型,得到所述含初始單點凹陷缺陷的非完美結構模型。
在上述網格開槽殼體的軸壓承載折減因子的預測方法中,所述對所述含初始單點凹陷缺陷的非完美結構模型進行非線性后屈曲分析,得到軸壓極限載荷,包括:
在初始單點上施加軸壓位移載荷,采用顯示動力學法進行后屈曲分析,直至所述網格開槽殼體的結構發生壓潰破壞,通過繪制軸壓位移載荷加載點的位移-反力曲線,得到軸壓極限載荷。
在上述網格開槽殼體的軸壓承載折減因子的預測方法中,所述通過改變所述單一指定位移載荷的大小,得到單點凹陷程度對軸壓承載的缺陷敏感性曲線,包括:
通過改變所述單一指定位移載荷的大小,重復執行步驟1-3,得到不同初始單點凹陷缺陷程度的軸壓極限載荷;
根據得到的不同初始單點凹陷缺陷程度的軸壓極限載荷,繪制得到所述單點凹陷程度對軸壓承載的缺陷敏感性曲線。
在上述網格開槽殼體的軸壓承載折減因子的預測方法中,所述根據所述單點凹陷程度對軸壓承載的缺陷敏感性曲線的收斂性,確定被引入單點凹陷缺陷程度,包括:
從所述單點凹陷程度對軸壓承載的缺陷敏感性曲線中,篩選得到滿足設定收斂閾值的被引入單點凹陷缺陷程度。
在上述網格開槽殼體的軸壓承載折減因子的預測方法中,所述根據所述單點凹陷程度缺陷對軸壓承載的敏感性曲線和所述單點凹陷位置對軸壓承載的缺陷敏感性曲線,得到所述網格開槽殼體的軸壓承載折減因子的預測結果,包括:
根據所述單點凹陷程度對軸壓承載的缺陷敏感性曲線和所述單點凹陷位置對軸壓承載的缺陷敏感性曲線,將軸壓極限載荷的下限值與不引入任何缺陷的完美結構模型軸壓極限載荷做比,得到比值結果;
根據所述比值結果,得到所述網格開槽殼體的軸壓承載折減因子的預測結果。
本發明具有以下優點:
本發明所述的網格開槽殼體的軸壓承載折減因子的預測方法,適用于金屬薄壁網格開槽殼體單點凹陷缺陷的建模和敏感性分析,引入缺陷模式簡單,建模高效,便于工程上快速得到此類網格開槽殼體的軸壓承載折減因子。其次,本發明揭示了網格開槽金屬殼體軸壓極限載荷對單點凹陷缺陷大小的敏感性規律,能夠快速評估凹陷大小對此類網格開槽殼體的軸壓承載效率的影響。此外,本發明還揭示了網格開槽金屬殼體軸壓極限載荷對單點凹陷缺陷位置的敏感性規律,能夠快速評估凹陷位置對此類網格開槽金屬殼體軸壓承載效率的影響。
附圖說明
圖1是本發明實施例中一種網格開槽殼體的軸壓承載折減因子的預測方法的步驟流程圖;
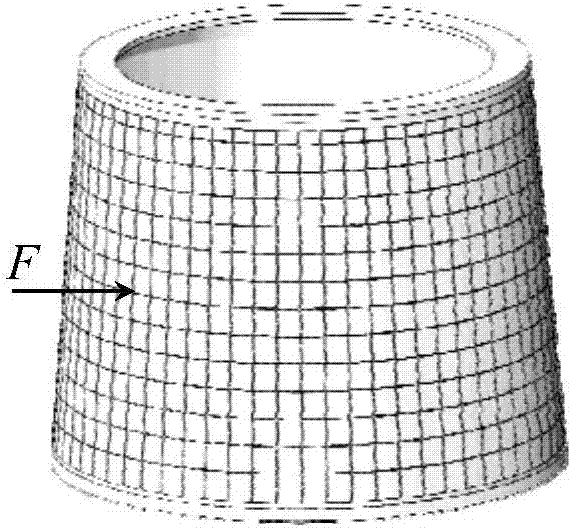
圖2是本發明實施例中一種截錐形網格開槽金屬殼體對應的有限元模型的示意圖;
圖3是本發明實施例中一種指定位移載荷作用下網格開槽結構變形情況示意圖;
圖4是本發明實施例中一種軸壓位移載荷加載點的位移-反力曲線示意圖;
圖5是本發明實施例中一種單點凹陷程度對軸壓承載的缺陷敏感性曲線示意圖;
圖6是本發明實施例中一種引入單點凹陷位置示意圖;
圖7是本發明實施例中一種單點凹陷位置對軸壓承載的缺陷敏感性曲線示意圖。
具體實施方式
為使本發明的目的、技術方案和優點更加清楚,下面將結合附圖對本發明公共的實施方式作進一步詳細描述。
本發明所述網格開槽殼體的軸壓承載折減因子的預測方法主要可以針對薄壁網格開槽殼體,考慮薄壁網格開槽殼體在加工、裝配、運輸和服役期間最易產生的外力撞擊凹陷,借助缺陷敏感性數值分析方法,對所述薄壁網格開槽殼體的軸壓承載折減因子進行預測。
參照圖1,示出了本發明實施例中一種網格開槽殼體的軸壓承載折減因子的預測方法的步驟流程圖。在本實施例中,所述網格開槽殼體的軸壓承載折減因子的預測方法,包括:
步驟101,建立網格開槽殼體對應的有限元模型。
在本實施例中,可以根據(薄壁)網格開槽殼體的具體結構,采用有限元分析法建立相應的有限元模型。例如,當所述網格開槽殼體為截錐形網格開槽金屬殼體時,可以采用六面體實體單元對所述網格開槽殼體為截錐形網格開槽金屬殼體進行離散,建立所述有限元模型。其中,所述截錐形網格每個節點包括三個平動自由度,所述有限元模型的下端固支,上端面節點與端面圓心位置參考點剛性耦合、且參考點除軸向位移外的其余所有自由度被約束。
步驟102,在網格開槽殼體中部橫縱開槽交匯位置施加單一指定位移載荷,根據所述有限元模型和施加的單一指定位移載荷,得到含初始單點凹陷缺陷的非完美結構模型。
優選的,在本實施例中,可以在網格開槽殼體中部橫縱開槽交匯位置施加單一指定位移載荷,采用非線性隱式靜力學法進行幾何大變形靜力分析,得到單點凹陷變形分布;然后,根據所述單點凹陷變形分布確定凹陷區域節點位移量。最后,將所述凹陷區域節點位移量疊加至有限元模型,得到所述含初始單點凹陷缺陷的非完美結構模型。
其中,所述網格開槽殼體中部橫縱開槽交匯位置可以是所述網格開槽殼體中部的任意適當位置,本實施例對此不作限制。
步驟103,對所述含初始單點凹陷缺陷的非完美結構模型進行非線性后屈曲分析,得到軸壓極限載荷。
在本實施例中,可以在初始單點上施加軸壓位移載荷,采用顯示動力學法進行后屈曲分析,直至所述網格開槽殼體的結構發生壓潰破壞,通過繪制軸壓位移載荷加載點的位移-反力曲線,得到軸壓極限載荷。
步驟104,通過改變所述單一指定位移載荷的大小,得到單點凹陷程度對軸壓承載的缺陷敏感性曲線。
在本實施例中,所述單點凹陷程度對軸壓承載的缺陷敏感性曲線可以用于指示不同初始單點的凹陷缺陷程度的軸壓極限載荷。具體的,可以通過改變所述單一指定位移載荷的大小,重復執行步驟101-103,進而得到不同初始單點凹陷缺陷程度的軸壓極限載荷;然后,根據得到的不同初始單點凹陷缺陷程度的軸壓極限載荷,繪制得到所述單點凹陷程度對軸壓承載的缺陷敏感性曲線。
步驟105,根據所述單點凹陷程度對軸壓承載的缺陷敏感性曲線的收斂性,確定被引入單點凹陷缺陷程度。
在本實施例中,可以從所述單點凹陷程度對軸壓承載的缺陷敏感性曲線中,篩選得到滿足設定收斂閾值的被引入單點凹陷缺陷程度。
步驟106,針對確定的被引入單點凹陷缺陷程度,通過改變單點凹陷的軸向位置,得到含初始單點凹陷缺陷的非完美結構模型集合。
在本實施例中,對于選定的被引入單點凹陷缺陷程度,考慮殼體軸向對稱性,單點凹陷缺陷的位置變量僅表現為沿殼體軸向的分布。因此,可以通過改變單點凹陷的軸向位置,得到一系列不同的含初始單點凹陷缺陷的非完美結構模型,也即,得到所述含初始單點凹陷缺陷的非完美結構模型集合,進而可以借助非線性后屈曲分析方法得到單點凹陷位置對軸壓承載的缺陷敏感性曲線。
步驟107,根據所述含初始單點凹陷缺陷的非完美結構模型集合,確定單點凹陷位置對軸壓承載的缺陷敏感性曲線。
步驟108,根據所述單點凹陷程度對軸壓承載的缺陷敏感性曲線和所述單點凹陷位置缺陷敏感性曲線缺陷敏感性曲線,得到所述網格開槽殼體的軸壓承載折減因子的預測結果。
在本實施例中,具體可以根據所述單點凹陷程度缺陷敏感性曲線缺陷敏感性曲線和所述單點凹陷位置缺陷敏感性曲線缺陷敏感性曲線,將軸壓極限載荷的下限值與不引入任何缺陷的完美結構模型軸壓極限載荷做比,得到比值結果;然后,根據所述比值結果,得到所述網格開槽殼體的軸壓承載折減因子的預測結果。
在本發明實施例中,為了便于理解,下面通過一個具體實例,對上述網格開槽殼體的軸壓承載折減因子的預測方法的具體實現進行詳細說明。
一、單點凹陷缺陷建模
參照圖2,示出了本發明實施例中一種截錐形網格開槽金屬殼體對應的有限元模型的示意圖。在本實施例中,所述截錐形網格開槽金屬殼體的具體參數可以如下:小端直徑800mm,大端直徑1000mm,高800mm,壁厚5mm,外側沿環向和母線方向開槽深2mm,鋁合金材料(zl114a),彈性模量e為71gpa,泊松比v為0.3,屈服極限為220mpa,強度極限為300mpa。
優選的,可以基于abaqus軟件建立所述截錐形網格開槽金屬殼體對應的有限元模型:采用六面體實體單元c3d8i對所述截錐形網格開槽金屬殼體進行離散;將上端面節點與端面圓心位置參考點進行剛性耦合且約束參考點除軸向位移外的其余所有自由度。其中,每個節點有三個平動自由度,所述截錐形網格開槽金屬殼體對應的有限元模型下端固支。考慮結構剛度分布特點,選取殼體中部任意橫縱開槽交匯位置,即最易發生單點凹陷位置施加單一指定位移載荷(如圖2所示的單一指定位移載荷f),采用非線性隱式靜力學法進行幾何大變形分析,得到單點凹陷變形分布;根據所述單點凹陷變形分布確定凹陷區域節點位移量;將所述凹陷區域節點位移量疊加至圖2所示的截錐形網格開槽金屬殼體對應的有限元模型中,得到如圖3所示的含初始單點凹陷缺陷的非完美結構模型。其中,圖3,示出了本發明實施例中一種指定位移載荷作用下網格開槽結構變形情況示意圖。
二、凹陷程度確定性分析
首先,針對上述含初始單點凹陷缺陷的非完美結構模型,仍然在模型下端施加固支約束,將上端面節點與圓心位置參考點進行剛性耦合且約束參考點除軸向位移外的其余所有自由度,在初始單點上施加軸壓位移載荷,采用顯示動力學法進行后屈曲分析,直至結構發生壓潰破壞,進而繪制得到軸壓位移載荷加載點的位移-反力曲線,根據繪制的軸壓位移載荷加載點的位移-反力曲線可以確定當前單點凹陷缺陷程度下的殼體軸壓極限載荷,即圖3中所示的曲線出現明顯向下拐點位置。其中,圖4,是本發明實施例中一種軸壓位移載荷加載點的位移-反力曲線示意圖。
其次,通過改變圖2中單一指定位移載荷f的大小,重復第一節的幾何大變形分析得到不同初始單點凹陷缺陷程度的非完美結構模型。在本實施例中,考慮殼體5mm壁厚實際情況,可以指定位移載荷f的大小在0~6mm范圍進行選取。
再次,對變化指定位移載荷大小所得到的一系列非完美結構模型,重復第二節中的后屈曲分析,即可得到一系列不同初始單點凹陷缺陷程度的軸壓極限載荷。
最后,可以根據得到的一系列不同初始單點凹陷缺陷程度的軸壓極限載荷,繪制得到指定位移載荷大小與結構軸壓極限載荷的關系曲線,即得圖5所示的單點凹陷程度對軸壓承載的缺陷敏感性曲線。其中,圖5,示出了本發明實施例中一種單點凹陷程度對軸壓承載的缺陷敏感性曲線示意圖。
此外,在本實施例中,可以根據下述公式(1)定義的收斂性判定要求,可以確定4mm指定位移載荷作用下的凹陷變形量為合理的初始缺陷程度。
其中,
三、凹陷位置敏感性分析
首先,由殼體軸對稱特性可知,單點凹陷缺陷的位置變量僅表現為沿殼體軸向的分布,選取殼體外側同一條母線方向上不同縱橫開槽交匯位置,如,可以選擇圖6中所示的點1-7為凹陷引入位置。其中,圖6,示出了本發明實施例中一種引入單點凹陷位置示意圖。
其次,分別依次在點1-7施加4mm指定位移載荷f,重復第一節的幾何大變形分析,得到一系列的不同初始單點凹陷缺陷位置的非完美結構模型。
再次,對不同初始單點凹陷缺陷位置所對應的一系列非完美結構模型,重復第二節中的后屈曲分析,便可得到相應一系列不同初始單點凹陷缺陷位置的軸壓極限載荷。
最后,可以根據得到的一系列不同初始單點凹陷缺陷位置的軸壓極限載荷,繪制得到的位移載荷位置與結構軸壓極限載荷的關系曲線,即得圖7所示的單點凹陷位置對軸壓承載的缺陷敏感性曲線。其中,圖7,示出了本發明實施例中一種單點凹陷位置對軸壓承載的缺陷敏感性曲線示意圖。
從圖7中可以看出:殼體中部缺陷敏感性最大,即當4mm指定位移載荷引起的初始凹陷缺陷位于殼體中部時(4號點),其軸壓極限載荷最低。進一步,在本實施例中,可以對中部的引入缺陷位置進行加密,增加如圖6中所示的點8和9,發現仍然是點4位置引入初始單點凹陷缺陷的軸壓極限載荷最低,此時殼體的破壞過程仍然表現為首先在較小的軸壓載荷下出現局部失穩,但結構仍能繼續承載,直至局部屈曲變形演化成為整體失穩波形。
四、折減因子預測
在本實施例中,可以借助圖5示出的單點凹陷程度對軸壓承載的缺陷敏感性曲線和圖7示出的單點凹陷位置對軸壓承載的缺陷敏感性曲線,確定所述兩條曲線(單點凹陷程度對軸壓承載的缺陷敏感性曲線和單點凹陷位置對軸壓承載的缺陷敏感性曲線)上軸壓極限載荷的最小值fmin,進而確定上軸壓極限載荷的最小值fmin與不引入任何缺陷的完美結構模型軸壓極限載荷f0的比值,并將該比值作為預測的該截錐形網格開槽金屬殼體的軸壓承載折減因子k:
在本實施例中,對比圖5(0mm指定移載荷作用下軸壓極限載荷2.32×106n)和圖7(4號點4mm指定位移載荷作用下軸壓極限載荷1.97×106n)的數據可以得出:該截錐形網格開槽金屬殼體的軸壓承載折減因子k為0.85。
綜上所述,本發明所述的網格開槽殼體的軸壓承載折減因子的預測方法,適用于金屬薄壁網格開槽殼體單點凹陷缺陷的建模和敏感性分析,引入缺陷模式簡單,建模高效,便于工程上快速得到此類網格開槽殼體的軸壓承載折減因子。其次,本發明揭示了網格開槽金屬殼體軸壓極限載荷對單點凹陷缺陷大小的敏感性規律,能夠快速評估凹陷大小對此類網格開槽殼體的軸壓承載效率的影響。此外,本發明還揭示了網格開槽金屬殼體軸壓極限載荷對單點凹陷缺陷位置的敏感性規律,能夠快速評估凹陷位置對此類網格開槽金屬殼體軸壓承載效率的影響。
本說明中的各個實施例均采用遞進的方式描述,每個實施例重點說明的都是與其他實施例的不同之處,各個實施例之間相同相似的部分互相參見即可。
以上所述,僅為本發明最佳的具體實施方式,但本發明的保護范圍并不局限于此,任何熟悉本技術領域的技術人員在本發明揭露的技術范圍內,可輕易想到的變化或替換,都應涵蓋在本發明的保護范圍之內。
本發明說明書中未作詳細描述的內容屬于本領域專業技術人員的公知技術。
- 還沒有人留言評論。精彩留言會獲得點贊!