一種適用于任意兩多邊形之間的內靠接臨界多邊形的計算方法與流程
本發明涉及二維坐標系統中幾何多邊形之間的內靠接臨界多邊形計算技術領域,特別是不規則多邊形之間的內靠接臨界多邊形的快速和準確的計算技術。
背景技術:
內靠接臨界多邊形計算問題廣泛存在于鈑金、服裝、木材、皮革、石材、玻璃等不規則原材料下料加工作業中,例如現代制造業中的鈑金切割、服裝裁剪、木材加工、皮革切割等下料作業,都需要采用專業的技術手段先在原材料上對需要加工或裁切的部件進行靠接排放,以獲得滿意的原材料利用率,這就需要計算各個部件相對于原材料的內靠接多邊形,使得各個部件能夠以較高的利用率擺放在原材料內部。
這些技術應用所涉及的科學問題在理論上稱為二維排樣優化問題,其研究內容是根據給定的原材料以及需加工的部件需求,確定部件在原材料上的最佳排放方案,以獲得最佳的材料利用率。由于問題具有組合特性和幾何特性,其計算難度很大。特別是在涉及不規則部件擺放在不規則原材料上,由于部件和原材料輪廓的不規則和任意性,問題的計算復雜度急劇增加,給優化問題的求解帶來極大困難。其中,如何確定不規則部件與不規則原材料之間的位置關系是基礎性問題。目前,原材料下料排樣多采用計算機技術自動完成。自動化排樣作為降低生產成本、提高工作效率的重要技術手段,在現代制造業中至關重要。
在尋找良好的排樣方案時,需要大量地考慮部件與原材料之間的緊密靠接,特別是不規則原材料排樣問題。如何確保部件能夠契合地擺放于原材料內部就是一個關鍵的基礎問題。要解決這一問題,需要使用準確、可靠和快速的內靠接臨界多邊形計算方法。兩個多邊形之間的內靠接臨界多邊形的幾何定義為:對于兩個形狀任意的多邊形a和b,讓多邊形a固定不動,多邊形b在a內部繞a的內部輪廓一周做不旋轉的平移運動,運動過程中保持b與a接觸但不重疊且位于a內部,那么b上預先選定的某個參考點在b的移動過程中所形成的一個或若干個封閉的多邊形就是b相對于a的內靠接臨界多邊形(集合)。內靠接臨界多邊形給出了二維部件(體現為多邊形)在原材料(體現為多邊形)內部可擺放的位置,其計算問題是二維排樣問題中的基礎性幾何問題,也是二維排樣應用中的關鍵技術問題之一。因此,一種快速、準確、適應性強的內靠接臨界多邊形計算方法是二維排樣問題的難點和重點,也是本發明主要解決的問題。
目前國內外眾多研究人員主要研究矩形或規則原材料的排樣問題,可以采用簡單的方法確定部件與原材料的相對位置。但是,對于不規則原材料(如皮革、石材或板材邊角料等),如何確定不規則部件在原材料中的相對位置尚無明確方法。本專利所述的內靠接臨界多邊形是一個相對于傳統所述的“外靠接臨界多邊形”而提出的全新概念,可用于描述一個多邊形在另外一個多邊形內部的所有可能的靠接位置。該概念恰可以用于描述不規則排樣問題中不規則部件與原材料之間的相對位置關系。本專利要解決的問題即為兩個形狀任意的多邊形之間的內靠接臨界多邊形的快速、準確計算。通過解決該關鍵基礎問題,推動排樣問題的研究,從而加快我國自動化排樣技術的發展。
就目前調研結果看,在國內尚無利用矢量線段合成方法計算兩個任意形狀多邊形之間的內靠接臨界多邊形的相關論文和專利授權。
技術實現要素:
本發明的主要目的在于提供一種適用于任意兩多邊形之間的內靠接臨界多邊形的計算方法。
為了便于準確描述,對發明所述方法中涉及的若干數學概念與數學符號作說明如下:
1、發明中所用的坐標空間均為平面坐標空間,并采用笛卡爾直角坐標系。為方便描述,假定水平向右方向為x軸正方向,水平向左方向為x軸負方向,垂直向上方向為y軸正方向,垂直向下方向為y軸負方向。
2、以符號a、b分別指代平面坐標系中兩個形狀任意的多邊形。為方便描述,本發明中所指的臨界多邊形均指多邊形b相對于多邊形a的內靠接臨界多邊形,即多邊形b在a內部繞多邊形a平移一周所形成的臨界多邊形。
3、多邊形a、b的表示方式既可采用多邊形輪廓的頂點集合表示方式,也可以采用多邊形輪廓的邊集合表示方式;頂點集合或邊集合的描述順序既可采用逆時針方向順序描述,也可以采用順時針方向順序描述。為方便描述,本發明以逆時針方向頂點集合的多邊形表示方法來描述輸入的部件和原材料信息和有關計算方法。
為了實現發明目的,本發明采用的計算方法的方案為:先反轉多邊形a表示方向(即采用順時針表示),再計算得到多邊形的角頂點(和矢量邊)相對于另一多邊形的能接觸的矢量邊(和角頂點)移動產生的矢量線段,對產生的矢量線段進行必要的分割處理后,對無效的矢量線段進行濾除,再對分割處理后的矢量線段采取“最小旋轉角”策略來合成可能存在的一個或多個內靠接臨界多邊形(包括可能存在的退化點或退化線)。
對于給定的任意形狀的兩個多邊形a、b,若需計算多邊形b相對多邊形a的內靠接臨界多邊形,方法具體包括如下步驟:
s1、將多邊形a的表示方向反轉,采用與多邊形b相反的方向。即將多邊形a轉為順時針方向表示。
s2、判斷一個多邊形的各個角頂點(矢量邊)與另一個多邊形各個矢量邊(角頂點)的接觸情況;
s3、多邊形的參考點選取。多邊形b輪廓邊上的任意一個點(包括其角頂點和矢量邊上的點)均可選為參考點。參考點一旦選定,在內靠接臨界多邊形的計算過程中不可更改;
s4、計算產生初始的矢量線段。利用步驟s2得到的能接觸的“角頂點-矢量邊”組合以及步驟s3選取的參考點,讓多邊形b的各個角頂點(和各矢量邊)在a的能接觸的矢量邊(和角頂點)上移動,此時參考點的移動將產生矢量線段;產生的所有矢量線段構成初始的矢量線段集合,兩個多邊形之間的內靠接臨界多邊形必定包含在上述方式產生的矢量線段之中;
s5、矢量線段的分割處理,此步驟對在步驟s4中計算產生初始的矢量線段進行分割處理;
s6、從矢量線段集合中濾除無效的矢量線段;通過此步驟處理,可得到后面合成內靠接臨界多邊形時所需的矢量線段集合。
s7、通過篩選矢量線段合成可能存在的一個或多個內靠接臨界多邊形。
s8、計算可能存在的退化情形。在一些特殊情況下,內靠接臨界多邊形可能會出現退化情形,包括退化為點和退化為線段兩種情形;
優選的,步驟s2中判定各個角頂點(矢量邊)與另一個多邊形各個矢量邊(角頂點)是否接觸,若角頂點的出邊相對于其入邊逆時針轉過的角度大于180度,則判斷角頂點和矢量邊不可能接觸;若不大于180度,且該矢量邊位于角頂點的入邊與出邊反向延長線所構成的逆時針方向夾角區域內,則判斷為兩者能接觸。通過此步驟,可計算獲得兩個多邊形的各個角頂點與各條矢量邊之間能接觸的所有“角頂點-矢量邊”組合。
優選的,步驟s4中初始的矢量線段集合的獲取包括兩個部分:
(1)、針對多邊形b的角頂點與多邊形a的矢量邊的每個能接觸“角頂點-矢量邊”組合,先平移多邊形b使其在組合中的角頂點與a中對應矢量邊的起點重合,然后沿矢量邊方向平移多邊形b,直到該角頂點到達該矢量邊的終點位置(且多邊形b在平移過程中始終保持其角頂點與該矢量邊相接觸),此過程中多邊形b的參考點的移動將產生一條矢量線段。通過這一計算,可產生一組基于多邊形b角頂點和多邊形a矢量邊的能接觸“角頂點-矢量邊”組合的矢量線段;
(2)、針對多邊形a的角頂點與多邊形b的矢量邊的每個能接觸“角頂點-矢量邊”組合,先平移多邊形b使其在該組合中的矢量邊的起點與a中對應的角頂點重合,然后沿該矢量邊的反方向平移多邊形b,直到該矢量邊的終點到達角頂點位置(多邊形b在平移過程中始終保持其矢量邊與該角頂點相接觸),此過程中多邊形b的參考點的移動也將產生一條矢量線段。通過這一計算,可產生一組基于多邊形a角頂點和多邊形b矢量邊的能接觸“角頂點-矢量邊”組合的矢量線段;
上述兩部分計算得到的兩組矢量線段構成本算法所需的初始的矢量線段集合。
優選的,步驟s5的矢量線段分割處理包括兩種情形:
①若矢量線段之間存在相交,其中兩線段重合或部分重合,以及一線段的端點與另一線段的端點重合不在此范疇內,則計算出它們的交點,并用交點分割該交點所在的矢量線段,每個交點都將其所在的矢量線段分割成兩條矢量線段;
②若某些矢量線段出現重合,其中長度相同的矢量線段完全重合的情形不在此范疇內,則用矢量線段位于重合部分的端點來分割矢量線段;
上述兩種情形的分割處理僅針對初始矢量線段集合中滿足所述兩種情形條件的矢量線段,分割得到的新矢量線段將加入矢量線段集合,而被分割的矢量線段則從集合中剔除;那些無需分割的矢量線段仍保留在集合中。
優選的,步驟s6中所述的無效的矢量線段包括完全位于多邊形a外部的矢量線段與部分位于a外部的矢量線段。
優選的,步驟s7中通過基于“最小旋轉角策略”的矢量線段篩選方法來嘗試合成可能存在的內靠接臨界多邊形;篩選方法遍歷當前矢量線段集合的所有端點,每次以一個端點作為出發點來進行一次內靠接臨界多邊形的合成嘗試,并確定可能存在的內靠接臨界多邊形;第一條矢量線段采用遍歷方式:分別以當前矢量線段集合中該出發點的各條出邊作為第一條矢量線段,進行多個輪次的矢量線段篩選和臨界多邊形合成嘗試;具體合成內靠接臨界多邊形的步驟如下:
s7.1、在以某條出邊作為第一條矢量線段進行一個輪次的合成嘗試操作時,首先以該線段的終點作為出發點、其矢量方向作為參考方向;
s7.2、基于最小旋轉角策略在該出發點的所有出邊中篩選出下一條矢量線段;
s7.3、以選中的矢量線段的終點作為新的出發點、其矢量方向作為新的參考方向,同樣采用最小旋轉角策略篩選出下一條矢量線段;后繼矢量線段的篩選方法以此類推,在每一輪次的篩選過程中,已被選中的矢量線段不再參與該輪次的后繼篩選,但是并不從矢量線段集合中刪除;
s7.4、在一個輪次的矢量線段篩選過程中,如果選中的矢量線段能夠形成一個封閉多邊形,且該封閉多邊形的點集方向正確,則該多邊形即為多邊形b相對于多邊形a的一個內靠接臨界多邊形;此時,再從矢量線段集合中剔除掉這個封閉多邊形所包含的所有矢量線段,從而完成一個輪次的內靠接臨界多邊形合成嘗試;
s7.5、在以矢量線段集合的每一個端點作為出發點進行臨界多邊形的合成嘗試過程中,所得到的所有有效的封閉多邊形就構成多邊形b相對于多邊形a的內靠接臨界多邊形集合。
更優選的,步驟s7.2、s7.3中所述的“最小旋轉角”策略,其中涉及到計算一條矢量線段相對于一個給定參考方向的旋轉角;該旋轉角定義為:參考方向所在的矢量邊繞其起點旋轉到與該矢量線段方向一致(或平行)時所轉過的角度;旋轉角的取值范圍為(-180,180],若參考方向是逆時針旋轉后與矢量線段方向一致,則旋轉角取正值;若是順時針旋轉后與矢量線段方向一致,則旋轉角取負值。
優選的,步驟s8退化點和退化線的具體情況如下:
①在矢量線段集合中,如果存在三條以上(含三條)的矢量線段相交于同一點,平移多邊形b使其參考點與該交點重疊,判斷此時的多邊形b是否在多邊形a內部;若是,則該點是一個退化為點的內靠接臨界多邊形(簡稱退化點)。
②在矢量線段集合中,如果存在兩條以上(含兩條)反向共線的矢量線段,且這些矢量線段與其它矢量線段存在兩個以上(含兩個)交點,則這在些交點中滿足退化點條件的兩個交點之間的線段是一個退化為線段的內靠接臨界多邊形(簡稱退化線)。
通過上述步驟計算得到的一個或多個內靠接臨界多邊形、退化點、退化線,共同構成了多邊形b相對于多邊形a的內靠接臨界多邊形(集合)。
本發明與現有技術相比,具有如下優點和有益效果:
1、本發明適用于任意兩多邊形之間的內靠接臨界多邊形的計算,在實際應用中不受零部件以及原材料(板材)輪廓的限制,適用面廣。
2、本發明在計算多邊形之間的內靠接臨界多邊形時大量采用矢量運算,具有較低的時間復雜度,能夠快速求得內靠接臨界多邊形,并與外靠接臨界多邊形方法結合,從而快速確定待排放零部件在原材料中的可能排放位置,為后續二維優化排樣奠定基礎。
3、本發明采用矢量線段合成方法計算內靠接臨界多邊形,除了內靠接臨界多邊形外,還能夠獲得可能存在的退化點或退化線的情況,計算更加準確和可靠。
附圖說明
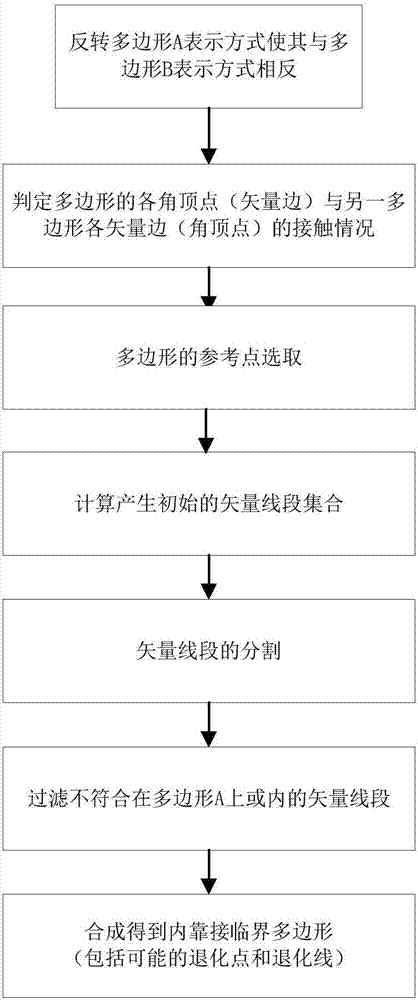
圖1是本發明的計算方法流程圖;
圖2(a)-圖2(c)是本發明的對多邊形a的反向預處理,即采用順時針方向表示,其中圖2(a)是多邊形b逆時針方向示意圖,圖2(b)是多邊形a逆時針方向示意圖;圖2(c)是多邊形a預處理后順時針方向的示意圖;;
圖3(a)-圖3(c)是本發明的一個多邊形的角頂點與另一多邊形的矢量邊的接觸判斷示意圖,其中圖3(a)是角∠cod的示意圖,圖3(b)是矢量邊
圖4(a)-圖4(d)是本發明的初始矢量線段集合的獲取示意圖,其中圖4(a)是多邊形b為逆時針方向的正方形,圖4(b)為多邊形a為逆時針方向不規則多邊形;圖4(c)多邊形b的角頂點在多邊形a的矢量邊上移動的示意圖;圖4(d)是多邊形b的矢量邊在多邊形a的角頂點上移動的示意圖;
圖5是本發明的矢量線段相交時的分割處理;
圖6(a)-圖6(d)是本發明的矢量線段重合時的分割處理;其中圖6(a)矢量線段方向相同、部分重合的情況;圖6(b)矢量線段方向相同、包含重合;圖6(c)矢量線段方向相反、部分重合;圖6(d)矢量線段方向相反、包含重合;
圖7是本發明的合成內靠接臨界多邊形的算法流程圖;
圖8是本發明的“最小旋轉角”策略;
圖9(a)-圖9(b)是本發明的內靠接臨界多邊形退化為點情形,圖9(a)表示表示多邊形b為一菱形,圖9(b)表示多邊形a為正方形;
圖10是本發明的內靠接臨界多邊形退化為線段的情形;
圖11(a)-圖11(c)是本發明的實施例基于矢量線段合成方法得到的完整的內靠接臨界多邊形集合,其中圖11(a)為多邊形b為逆時針方向的正方形,圖11(b)為多邊形a為預處理后為順時針方向的不規則多邊形,圖11(c)為采用本發明所述方法計算得到的多邊形b相對于多邊形a的內靠接臨界多邊形集合。
具體實施方式
下面結合實施例及附圖對本發明作進一步詳細的描述,但本發明的實施方式不限于此。
實施例
為了便于準確描述,對發明所述方法中涉及的若干數學概念與數學符號作說明如下:
①發明中所用的坐標空間均為平面坐標空間,并采用笛卡爾直角坐標系。為方便描述,假定水平向右方向為x軸正方向,水平向左方向為x軸負方向,垂直向上方向為y軸正方向,垂直向下方向為y軸負方向。
②以符號a、b分別指代平面坐標系中兩個形狀任意的多邊形。為方便描述,發明書中所指的臨界多邊形均指多邊形b相對于多邊形a的內靠接臨界多邊形,即多邊形b在a內部繞多邊形a平移一周所形成的臨界多邊形。
③多邊形a、b的表示方式既可采用多邊形輪廓的頂點集合表示方式,也可以采用多邊形輪廓的邊集合表示方式;頂點集合或邊集合的描述順序既可采用逆時針方向順序描述,也可以采用順時針方向順序描述。為方便描述,本發明以逆時針方向頂點集合的多邊形表示方法來描述輸入的部件和原材料信息和有關計算方法。
如圖1所示為本發明的計算方法流程,包括如下步驟:
(1)反轉多邊形a的表示方向使其與多邊形b反向。如圖2(a)、圖2(b)中,多邊形a、b初始均以逆時針方向表示,反轉多邊形a則使a采用順時針方向表示,如圖2(c)所示。
(2)判斷多邊形的角頂點與另一多邊形的矢量邊的接觸情況。如圖3(a)中,判斷角∠cod的頂點o能否與矢量邊
(3)選取多邊形參考點。若求取多邊形b相對多邊形a的臨界多邊形,則選取多邊形b輪廓上的任一點作為參考點。參考點一旦選定,則在內靠接臨界多邊形的計算過程中不可更改。在實際應用中,為方便計算,通常選取多邊形的某個處于極限位置的頂點作為參考點。
(4)計算獲取初始矢量線段集合。求解過程為:針對步驟(2)獲得的多邊形b與多邊形a的各個角頂點與各條矢量邊的能接觸組合,移動多邊形b使其矢量邊沿著可接觸的多邊形a的角頂點移動,以及移動多邊形b使其角頂點沿可接觸的a的矢量邊移動,此過程中參考點移動得到的多條線段構成初試的矢量線段集合。整個過程中,多邊形a固定,多邊形b移動。圖4所示為初始矢量線段集合的獲取,其中圖4(a)、圖4(b)中多邊形b為逆時針方向的正方形,多邊形a為逆時針方向、帶有凹糟的不規則多邊形,參考點選取的是多邊形b的左下角頂點;圖4(c)中的虛線為多邊形b的角頂點在多邊形a的矢量邊上移動產生的矢量線段,圖4(d)中的虛線為多邊形b的矢量邊在多邊形a的角頂點上移動產生的矢量線段。為了便于觀察,圖中有重合的矢量線段做了微平移處理。
(5)分割矢量線段。在初始矢量線段集合中,若矢量線段之間存在相交或重合,則用矢量線段的交點或位于重合部分的端點分割相關矢量線段,得到分割后的矢量線段集合。包括兩種可能情況:
①若矢量線段之間存在相交(兩線段重合或部分重合,以及一線段的端點與另一線段的端點重合不在此范疇內),則計算出它們的交點,并用交點分割該交點所在的矢量線段,每個交點都將其所在的矢量線段分割成兩條矢量線段。圖5舉例說明了矢量線段相交時的分割方法。圖中矢量線段
②若某些矢量線段出現重合(長度相同的矢量線段完全重合的情形不在此范疇內),則用矢量線段位于重合部分的端點來分割矢量線段,分割方法與矢量線段的方向以及重合形式有關。圖6(a)-圖6(d)舉例說明了矢量線段重合時的分割方法。圖6(a)為兩條同向且為部分重合的矢量線段的分割:同向矢量線段
(6)濾除矢量線段集合中無效的矢量線段。無效的矢量線段指全部或部分位于多邊形a外部的矢量線段。濾除操作將位于無效的矢量線段從矢量線段集合中刪除,從而得到后面合成內靠接臨界多邊形時所需的矢量線段集合。
(7)合成內靠接臨界多邊形。如圖7為計算內靠接臨界多邊形的算法流程圖。通過遍歷矢量線段的端點集合,以每個端點作為初始的出發點(起點),采用“最小旋轉角”策略,經過多個輪次來篩選矢量線段和嘗試合成內靠接臨界多邊形。其中,圖8所示為利用最小旋轉角策略從出發點的所有出邊中篩選出一條用于合成內靠接臨界多邊形的矢量線段的示例。假定圖中
(7)計算可能存在的退化點和退化線。
在一些特殊情況下,內靠接臨界多邊形可能會出現退化情形。包括兩種:內靠接臨界多邊形退化為點或退化為線段。退化點與退化線均屬于內靠接臨界多邊形的范疇,其確定方法分述如下:
①在矢量線段集合中,如果存在三條以上(含三條)的矢量線段相交于同一點,平移多邊形b使其參考點與該交點重疊,判斷此時的多邊形b是否在多邊形a內部。若是,則該點是一個退化為點的臨界多邊形(簡稱退化點)。圖9(a)、圖9(b)為臨界多邊形退化為點的示例,多邊形b為一菱形,多邊形a為正方形,參考點選取為多邊形b的最下角頂點,利用多邊形a、b計算得到的部分矢量線段(圖中所示的4條帶方向箭頭的虛線)相交于一點(o),平移多邊形b使得其參考點(最下端點)與o點重合后,因多邊形b在多邊形a內部,故o點為退化點。
②在矢量線段集合中,如果存在兩條以上(含兩條)反向共線的矢量線段,且這些矢量線段與其它矢量線段存在兩個以上(含兩個)交點,則這在些交點中滿足退化點條件的兩個交點之間的線段是一個退化為線段的內靠接臨界多邊形(簡稱退化線)。圖10為圖4(b)中所示的多邊形b相對于多邊形a所求得的矢量線段集合,其中,多邊形b為一正方形,多邊形a為帶凹糟的不規則多邊形,參考點選取為多邊形b的左下角頂點。用多邊形a、b計算得到的部分矢量線段有:
最終,通過上述步驟計算得到一個或多個內靠接臨界多邊形、退化線、退化點,共同構成兩個多邊形之間的內靠接臨界多邊形集合。如圖11(a)-圖11(c)所示,多邊形b為逆時針方向的正方形,多邊形a為預處理后為順時針方向、帶有凹糟的不規則多邊形,參考點選取的是多邊形b的左下角頂點。圖11(c)中實線線段的集合即為采用本發明所述方法計算得到的多邊形b相對于多邊形a的內靠接臨界多邊形集合。其中,多邊形cde和多邊形ghij為具有多邊形形態的內靠接臨界多邊形,線段ef和線段fg則為退化為線段的內靠接臨界多邊形。當多邊形b的參考點位于臨界多邊形的任一點上時,多邊形b與多邊形a之間均為既靠接且無重疊的狀態。
上述實施例為本發明較佳的實施方式,但本發明的實施方式并不受上述實施例的限制,其他的任何未背離本發明的精神實質與原理下所作的改變、修飾、替代、組合、簡化,均應為等效的置換方式,都包含在本發明的保護范圍之內。
- 還沒有人留言評論。精彩留言會獲得點贊!