一種計及光伏出力不確定性和全壽命周期成本的配電網變壓器規劃方法與流程
本發明一種計及光伏出力不確定性和全壽命周期成本的配電網變壓器規劃方法,屬于含分布式電源(distributedgeneration,dg)配電網規劃領域。
背景技術:
近年來,隨著環境污染和能源短缺問題的不斷加重,分布式發電技術愈加受到重視。在配電網中,分布式電源,尤其是分布式光伏發電(photovoltaicgeneration,pvg)的滲透率正在迅速增長,在此背景下,如何進行科學的電力設備投資決策,建設可靠經濟的配電網是目前規劃領域的研究熱點。
配電變壓器(配變)是配電網中重要的電力設備,使用量大、應用范圍廣、運行時間長,節能潛力巨大。長期以來,配變投資規劃重點關注初始投資或階段性成本,忽視了設備在后期運行、退役處置等整個服役周期中的潛在費用,從而導致其容量及型號的選擇缺乏貫穿設備全壽命周期的整體視角,容易形成過于保守或激進的規劃方案,造成較大的投資浪費。鑒于此,基于全壽命周期理論(lifecostcycle,lcc)的配變投資決策方法已經逐漸得到認識和應用,其主要是在保證規劃可靠性的基礎上,通過精確計算配變從購置、運行、維修和退役回收整個服役周期內(即全壽命周期)的價值特性變化規律,實現對配電科學的定容選型。同時研究發現,目前在配變規劃中雖實現了對配變lcc成本的精確評估,但依然存在一定問題:一方面,規劃時均未考慮配電網中的不確定性因素影響,而隨著大量分布式電源接入配電網,配電網規劃過程中的不確定影響因素進一步增多,這種基于確定性lcc成本的配變規劃因其無法對不確定性因素的影響進行精確評估,已經難以滿足現有含分布式電源配電網規劃的實際需求;另一方面,目前大多數僅針對固定容量下的配變選型問題,在規劃過程中,是將配變定容和選型割裂為兩個獨立問題分別進行計算,這有可能忽視前者對于配變選型的內在影響,從而影響規劃模型的計算精度。
目前,精確考慮不確定性因素的規劃方法在電源規劃、線路網架規劃領域已經得到一定程度的應用。諸如利用諸如機會約束、魯棒優化等不確定性建模方法,構建計及不確定性因素影響的規劃模型,從而解決了分布式電源接入后電網的一系列規劃問題,為配變規劃問題研究提供了良好的參考和借鑒。
技術實現要素:
針對分布式光伏發電接入后的配變規劃問題,本發明提出了一種計及光伏出力不確定性和全壽命周期成本的配電網變壓器規劃方法,首先,基于機會約束理論,構建配變容量計算的風險模型,確定不同置信區間下的最佳配變容量,在此基礎上提出基于三點估計法的配電網概率潮流計算方法,并將其作為約束條件納入到規劃模型之中,然后考慮配變容量選擇對投資成本和運行成本的影響,提出配變lcc成本的數學表達方式,最終建立以lcc成本最小化為目標的不確定性配變規劃模型。
本發明采取的技術方案為:
一種計及光伏出力不確定性和全壽命周期成本的配電網變壓器規劃方法,包括以下步驟:
步驟1:基于機會約束理論的配變容量規劃。
步驟1.1:根據實際情況,確定規劃區域光伏出力概率模型和負荷波動概率模型;
步驟1.2:依據臺區實際負荷數據,建立基于機會約束的臺區配變容量規劃模型。
步驟2:基于全壽命周期理論的不確定性配變選型建模。
步驟2.1:建立基于全壽命周期理論的配變選型目標函數;
步驟2.2:考慮光伏出力和負荷波動不確定性的配變運行成本精細化分析。
步驟3:基于三點估計法的概率潮流模型求解方法。
通過上述步驟,完成計及光伏出力不確定性和全壽命周期成本的配電網變壓器規劃。
本發明提出了一種計及光伏出力不確定性和全壽命周期成本的配電網變壓器規劃方法,技術效果如下:
1):相比于傳統配電變壓器定容選型方法,本發明中提同時考慮了光伏發電出力不確定性的影響和配變的全壽命周期成本,提出了一種不確定性的lcc規劃方法,有效避免得出保守或者冒進的規劃方案,提升了規劃的精細化水平。
2):相比于傳統配電變壓器定容選型方法,充分考慮了配變容量選擇對配變選型中投資成本和運行成本的影響,實現了配變定容和選型問題的統一,提升了規劃精細化水平。
附圖說明
圖1為本發明基于三點估計法的概率潮流模型求解流程圖。
圖2為本發明實施例迭代收斂曲線圖。
圖3為本發明不同預測模型預測誤差概率密度對比擬合曲線圖。
圖4為方法1下不同綜合選型方式下配變lcc成本圖。
具體實施方式
一種計及光伏出力不確定性和全壽命周期成本的配電網變壓器規劃方法,其具體實施方式如下
步驟1:基于機會約束理論的配變容量規劃:
步驟1.1:根據實際情況,確定規劃區域光伏出力概率模型和負荷波動概率模型。
通常將一定時間段內的光照強度近似采用beta分布來描述:
式中:i為光照強度,ir表示該時間段內最大光照強度;α和β為beta分布的兩個參數;γ(·)為伽瑪函數。
pvg出力與光照強度之間的關系可以近似表示為:
式中:ppvg為光伏出力有功功率大小;
依據隨機變量的函數分布定理,同時結合式(1)、式(2)推導出光伏機組出力的概率密度函數為:
式中:qpvg為光出出力的無功分量;
通常近似采用正態分布來描述負荷波動特性:
式中:pl為負荷的有功分量;μp、σp為負荷有功分量的期望和標準差;ql為負荷的無功分量;θ表示為負荷的功率因素角。
步驟1.2:基于機會約束的臺區配變容量規劃模型的建立:
利用機會約束理論處理光伏接入負荷側后出力的不確定性,臺區上級電網所提供的有功功率pn和光伏有功出力ppvg之和小于臺區所需有功功率pl的概率應不超過給定的置信度e:
f{pn+λppvg≤pl}≤e(5)
式中:f{·}表示{·}中事件成立的概率;λ表示光伏直供用戶出力占總出力的比例;置信度e根據地區實際經濟社會發展狀況人為給定。
聯立公式(3)和(5)可得:
已知臺區負荷所需有功功率pl,由上式可確定給定置信度下的網供負荷pn,同時設臺區負荷的增長全部由pn來承擔,根據公式(7)可確定配變裝接容量:
式中:
步驟2:基于全壽命周期理論的不確定性配變選型建模:
步驟2.1:選型目標函數的建立:
配變選型規劃模型的目標函數如下:
minct=ci+cw+co+cf+cr(8)
式中:ct為周期t內配變lcc成本;ci為配變初始投資成本;cw為配變的運行成本;co為變配變的檢修維護成本;cf為配變的故障成本;cr為配變的退役處置成本。
步驟2.2:考慮光伏出力和負荷波動不確定性的配變全壽命周期內各階段成本詳細模型
1)配變初始投資成本ci:
配變初始投資成本主要包括配變購置費cgz和安裝調試費caz,其主要受變壓器容量大小及型號選擇的影響:
式中:配變安裝調試費一般為購置費的6.2%;
2)、考慮光伏出力和負荷波動不確定性的配變運行成本cw分析:
配變運行成本主要包括配變運行能耗成本cnh和日常巡檢成本ccs。
式中:
式中:
考慮到光伏出力及負荷波動的不確定性,無法直接根據銘牌參數對配變運行負載損耗進行精確度量,鑒于此,本發明研究引入概率潮流模型對配電網變壓器支路配變負載損耗精確進行求解,概率潮流模型如下所示:
式中:pa和qa分別表示節點a有功功率及無功功率注入量;w表示配電網節點數;va和vb分別表示節點a和節點b的電壓幅值;rz和xz分別為臺區支路線路電阻和電抗;rb和xb分別為配變電阻和電抗;gab和bab分別表示節點導納矩陣的實部和虛部;δab表示節點a節點b的相角差。
3)、配變檢修維護成本co:
配變檢修維護成本主要包括了配變運行壽命周期的大修費用cdx和小修費用cxx,配變通常情況下使用壽命為20年~25年,配變在投入運行后,每年進行一次小修,第5年進行一次大修,之后每隔10年進行一次大修。此項成本與配變容量大小和型號無關,其計算公式如下:
式中:cdx表示單次大修費用;cxx表示單次小修費,u表示大修次數;floor(·)表示小數向下取整。
4)、配變故障成本ccf:
配變故障成本主要包括配變故障檢修費用和故障損失費用。此項成本與配變容量及型號選擇有關。可以由下式表示:
式中:ccf為年故障費用;kd為電價折算倍數,一般取kd=15;tg年平均事故停電時間,tg=ε×24;ψi表示第t年配變平均負載率;ε為配變年事故率,配變型號越好,事故率越低;cjx為故障檢修費用,一般取設備購置費的3%;ε為配變年故障率。
5)、配變退役處置成本ccd:
配變退役處置成本主要包括配變報廢成本和設備殘值費。其設備殘值費同配變容量和型號正相關。表示如下:
式中:cbf為設備報廢成本,一般取設備安裝費的32%;ccz為設備殘值費,一般為購置費的5%。
步驟2.3:約束條件:
1)、節點電壓和支路電流約束
式中:vimin和vmax分別為第i個節點電壓幅值的最小值和最大值;ij和
2)、dg接入節點安裝容量約束:
式中:si.dg為第i個節點dg接入節點安裝容量;
3)、配變型號及容量離散性約束:
設集合a為配變設計容量等級,集合b為待選配變型號,存在以下約束條件:
步驟3:基于三點估計法的概率潮流模型求解方法:
設臺區配變單位負載損耗△sf與光伏出力和臺區負荷的函數關系如下:
式中:△sw為臺區配變所在支路損耗;
令單位負載損耗△sf用隨機變量y表示,光伏出力和臺區負荷用隨機變量x表示,式(12)簡化為:
y=ζ×f(x)=ζ×f(x1,x2…,xn)(20)
式中:n表示隨機變量x的總數。
假定每一個隨機變量的xk(k=1,2,3…n)的期望、標準差分別為μk和σk,并選取隨機變量xk的期望μk及其左右領域內各一點共三個采樣值,記作xk.i(i=1,2,3),其表達式如下:
xk.i=μk+ξk.iσk(i=1,2,3)(21)
式中:ξk.i為第k個隨機變量第i個采樣值的位置系數。ξk.i可表示為:
式中:λk.3表示為隨機變量xk的偏度系數,其絕對值越大,則說明隨機變量xk的分布與標準正太分布偏離較大;λk.4為衡量隨機變量xk的概率密度在期望值附近的陡峭程度的峰度系數,其絕對值越小,隨機變量的取值在期望值附近更集中,λk.4=0,則說明隨機變量xk的分布和標準正態分布具有一樣的陡峭度。xk的偏度系數λk.3和峰度系數λk.4的表達式分別為:
式中:e[(xk-μk)3]、e[(xk-μk)4]為隨機變量xk的三階、四階中心矩。
采樣值xk.i(i=1,2,3)分別所對應的權重系數pk.i為:
由公式(23)~公式(24)可知,三點估計法本質上是根據輸入隨機變量的前四階矩確定樣本采樣值xk.i(i=1,2,3),并利用如公式(25)所示的確定性函數關系對每一個采樣值進行確定性評價。
yk.i=ζ×f(μ1…,μk-1,xk.i,μk+1…,μn)i=1,2,3(25)
值得注意的是,因為每一個隨機變量采樣的時候都包含了其期望值μk,所以其中有n次確定性評價是重復的,所以只需對y進行2n+1次評價即可。根據上述結論,結合采樣點所對應的權重系數,y的z階原點矩可以表示為:
得到輸出變量y的各階矩后,就可以求出其期望μy和標準差σy,即臺區配變單位負載損耗期望及方差。
詳細求解計算流程圖如附圖1所示。
實施例:
本發明以修改后的ieee33配電網節點系統作為算例,驗證本發明所提出的配變選型定容方法的有效性和正確性。仿真試驗均在matlab環境下編程實現。
1)、修改的ieee33節點系統:
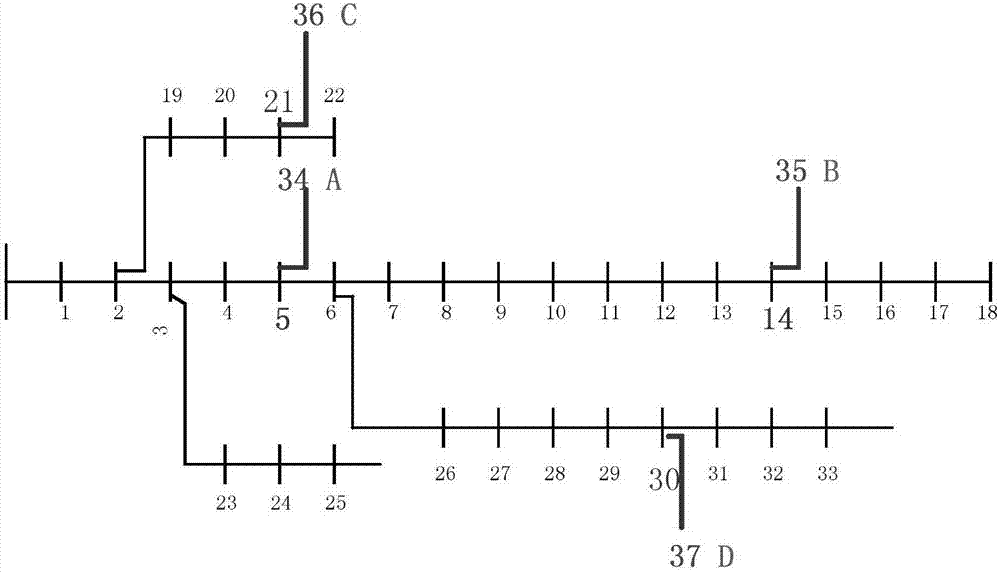
假設一區域新增臺區a、b、c、d,對應負荷節點34、35、36和37,設各新增臺區負荷基準值分別為50kva、70kva、90kva和110kva且均服從正態分布(期望為對應節點負荷基準值,方差為1),各臺區配變的阻抗分別折算到相應的支路阻抗參數中。設節點5、14、21和37分別有100kw、150kw、200kw和250kw的光伏機組接入,取為0.85,各光伏機組有功出力服從參數、的beta分布。修改后的ieee33配電網節點系統如圖1所示。電壓等級為12.66kv,基準功率為100mva,聯絡開關斷開。
設該區域年均負荷增長率為0.05,待選取新型變壓器型號有scb10系列、scb11系列和scb13系列干式10kv變壓器,變壓器詳細技術參數見附錄,設計配變壽命周期為20年,現需針對臺區a、b、c、d進行綜合配變定容與選型規劃。
修改的ieee33節點配電網如附圖2。
2)、算例仿真結果及分析:
驗證本發明方法的正確性和有效性,分別利用三種方法對本發明算例進行配變規劃決策:
方法1:本發明所提出的計及光伏出力不確定性和全壽命周期成本的配變規劃方法,置信度取0.01,負荷年均增長率取為0.05。
方法2:考慮配變運行工況及全壽命周期成本的確定性配變規劃方法。此時,忽略dg出力和負荷波動的不確定性影響,因此針對配變容量選取時,置信度取為0;在進行配變選型時,光伏出力及新增負荷點參數根據各自概率密度函數取期望值進行常規確定性潮流計算,其他參數設置同方法1。
方法3:考慮全壽命周期成本的配變模糊規劃方法。此時,將配變運行工況模糊化處理,忽略dg出力和負荷波動,針對配變容量選取時,置信度取為0;在進行配變選型時,不參考潮流計算結果,僅依據配變銘牌參數對配變lcc進行粗略估算;同時不考慮各臺區定容選型結果對潮流的影響,各臺區進行獨立的定容與選型。
①:方法1的仿真結果及分析:
利用本發明所提方法,求解算例中a、b、c、d四個臺區配變容量在不同置信區間下的變化情況如附圖3所示。
考慮到實際情況下scb10系列、scb11系列和scb13系列臺區配變出廠設計容量,依據附圖3可以給出不同置信區間下的各臺區配變容量選定結果如表1所示。
表1各臺區不同置信下的配變定容結果
由附圖3、表1可知,配變規劃容量與置信概率負相關,其原因是在不確定性環境下,置信度取值越低,意味著系統規劃過程中所冒風險越小,因而選取的配變容量越大,由此可見本發明方法可以在配變容量選擇過程中實現對系統運行風險的精細化度量;而配變容量選擇也會受到系統負荷的影響,系統負荷越大,配變規劃容量越大。
假設置信度取值0.01,則依據表1可以確定出臺區a、b、c、d配變容量分別定為250kva、315kva、400kva、500kva。以此為基礎,利用本發明配變選型規劃方法(方法1)可以得到臺區a、b、c、d在81種不同的綜合配變選型方式下所對應的lcc總成本如附圖4所示。
由圖4可以發現:第42種臺區配變綜合選型方式(臺區a:scb11、臺區b:scb11、臺區c:scb11、臺區d:scb13)將會使臺區a、b、c、d未來20年的lcc總成本達到最小,此時的綜合選型結果達到最優。
為進一步研究置信度對于配變選型結果的影響,按照上述方法,令置信度取值區間為0.01~0.2,步長取0.01,在相同條件下對四個臺區進行綜合配變定容及選型,得到不同置信區間下a、b、c、d四個臺區綜合配變定容與選型結果如表2所示:
表2不同置信度下的配變綜合定容選型結果
由表2可以發現,不同置信度下的臺區配變的容量選擇和型號選擇結果不斷發生變化,同時最優的lcc成本隨置信度的逐漸增加呈先降后升的特征。在置信區間[0.01~0.06]內,四個臺區配變lcc總成本隨著置信度整體增大而減小;而在置信度[0.07~0.2]的區間內,lcc成本則隨著置信度增大而增大,且增長速度越來越快。在本發明算例中,當置信度取為0.07時,配變lcc成本達到最小,各臺區配變綜合定容及選型達到最優。
出現這種現象的主要原因是:在置信區間[0.01~0.06]內,配變容量選擇相對較大,型號選擇相對較好,配變運行損耗較低,隨著風險的增加,配變在容量及型號選擇上節約的投資成本比增長的運行成本更多;而在置信度[0.07~0.2]的區間內,隨著配變容量選擇越來越小,型號選擇越來越差,配變本身的阻抗逐漸增加,且增長速度越來越大,配變運行損耗較大,導致節約的投資成本難以抵消掉配變急劇增長的運行成本。
②方式2、方式3仿真結果及對比分析:
相同條件下,利用方式2和方式3對本發明算例中a、b、c、d四個臺區進行配變綜合定容與選型,并與方法1進行對比,結果如表3所示。
表3不同規劃方法下的下的配變定容選型結果
由表3可以發現:①方法2下,臺區b與臺區c較方法1分別增加了85kva和100kva,臺區b與臺區d選擇的配變型號更加優良,lcc總成本增加了6.1647萬元。其主要原因是:方法2下的配變規劃置信度取為0,意味著在配變的定容選型時沒有冒任何風險,從而導致配變容量較方法1下選取整體較大,型號選擇整體較好,進而影響配變初始投資成本也隨之增長,同時在配變整個壽命周期內,方法2下的規劃方案在運行成本上的優勢無法彌補其在初始投資上的劣勢,導致lcc總成本較方法1更大。②方法3下各臺區配變容量規劃結果與方法2相同,但在配變選型上,臺區a、b、c選擇更加優良,lcc總成本增加了21.2029萬元。其主要原因是:在配變容量選取上,方法3與方法2都在置信度為0的情況下進行確定性定容規劃,導致容量選取結果一樣,而在配變選型方式上,方法3不考慮配電網實際潮流運行結果,直接利用配變銘牌上所標定的負載損耗進行lcc核算,往往會導致核算結果比實際情況更大,從而使計算的運行成本虛高,進而導致配變選型較方法2更加保守。
綜上所述,由于本發明方法在對光伏出力不確定性和負荷波動進行精確度量的同時,還充分考慮了配變容量對其型號選擇的影響,因而所得出的規劃方案較傳統方法而言,具有更高的經濟性,從而有效提升了配電網規劃的精細化水平。
本發明按照優選實施例進行了說明,但上述實施例不以任何形式限定本發明,凡采用等同替換或等效變換的形式所獲得的技術方案,均落在本發明技術方案的范圍內。
- 還沒有人留言評論。精彩留言會獲得點贊!